

坂田先生
ここでは、3点の座標から三角形の面積を求める公式2パターンについて手短に解説しています。
合わせて学習したい一次関数
参考:2点から等距離にある直線の式の求め方2通りと公式3つ
参考:3点から等距離にある点の座標の求め方3通り
参考:線分の垂直二等分線の方程式の求め方2通りと公式
3点から三角形の面積を求める公式1

にゃんこ
3点のうち1点が原点を通る場合

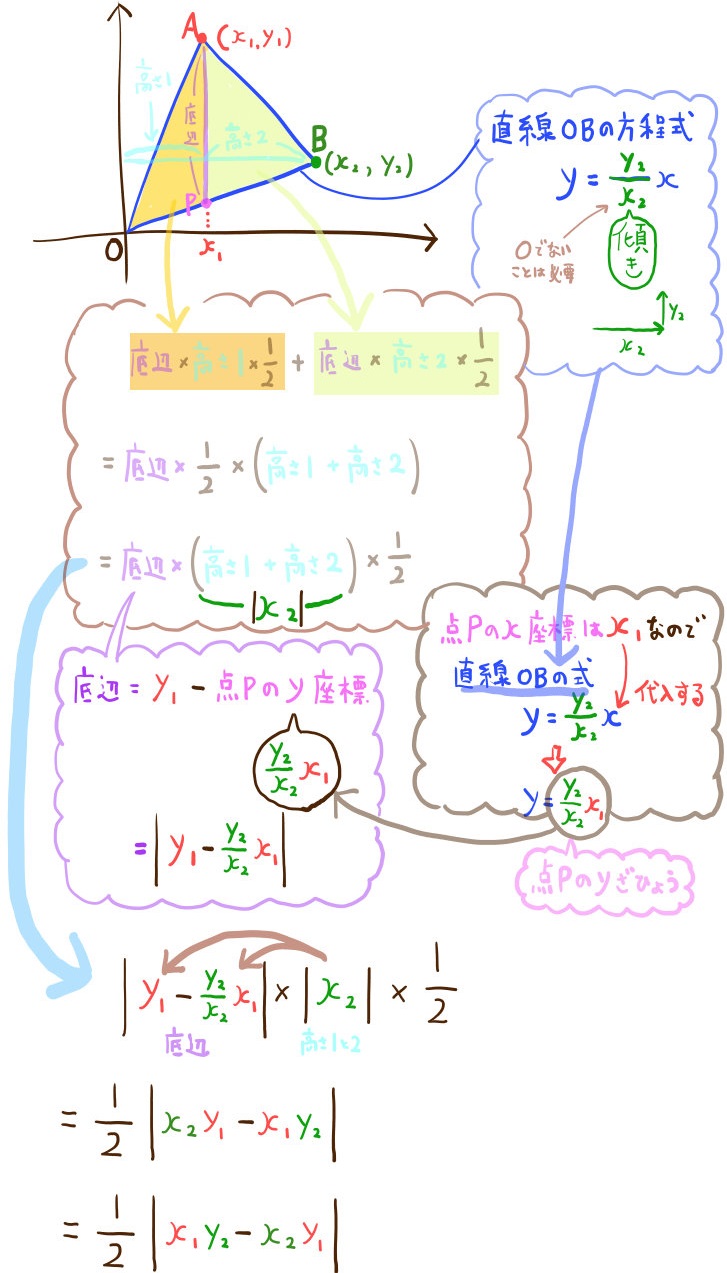

にゃんこ
公式の証明を図解にしています。

坂田先生
重要なポイントは座標平面上における長さはすべて正の数なので、2点間の距離をとった場合、絶対値の記号をつけて計算表現しなければならない、という所です。
3点から三角形の面積を求める公式2

坂田先生
3点とも原点を通らない場合(後半、詳しく説明します)

ご注意ください

坂田先生
ちなみに中学数学ではこのように解いていました。
【中学の復習】座標平面上の三角形の面積の求め方3通り
- 2つの三角形に分解してそれぞれの面積を求める
- 等積変形によって三角形の形を変化させてから面積を求める
参考:等積変形を利用し座標平面上の三角形の面積を求める手順 - 三角形が内接する長方形の面積を求めてから不要な部分を引き算する

にゃんこ
それでは以下、この2つの公式について詳しく説明していきます。
3点から三角形の面積を求める公式(原点を通る場合)

坂田先生
それでは公式の解説をしていきます。

にゃんこ
座標平面上の三角形の面積を求める際、頂点のどれからが原点を通る場合、以下の公式を使うことができます。


坂田先生
これだとピンとこないと思いますので、具体的な数字を持ち出して解説します。
例題:3点(0、0)(5,-1)(2,8)を頂点とする三角形の面積を求めよ。

にゃんこ
公式に当てはめるとこうなります。


坂田先生
内と内、外と外、なんていう説明の仕方をしていますが、比例式でもなんか聞いたことありますよね。

にゃんこ
ともかく、内と内、外と外をかけたもの同士を準備して、順番はいいから差をとって絶対値の記号をつける、と覚えておきましょう。

坂田先生
最後にそれを半分にして完了です。
3点から三角形の面積を求める公式(3点とも原点を通らない場合)

にゃんこ
続いて原点を通る点がない場合の公式です。

坂田先生
これは具体的な数値で最初の説明を聞いたほうがわかりやすいので、まずこれをご覧ください。
例題:3点(4、9)(7,6)(2,3)を頂点とする三角形の面積を求めよ。

にゃんこ
これはまず、各頂点のx座標を-2、y座標を-3して、点(2,3)が原点を通るように、3点をすべて平行移動させます。

坂田先生
そうすることで、さきほど学習した3点の頂点の座標から三角形の面積を求める公式を使えるようになります。


にゃんこ
このように、いちいち座標平面を書いて求めなければいけないかというと、そうでもありません。

坂田先生
例えば上と同じ頂点の座標を使って、次のように出題された場合、このように計算するとわかりやすいと思います。
例題:3点(4、9)(7,6)(2,3)を頂点とする三角形の面積を求めよ。

どうでしょうか。
3点(4、9)(7,6)(2,3)から
3点(2、6)(5,3)(0,0)へと
下準備をしてから計算すると、スムーズに三角形の面積を求めることができるかと思います。

にゃんこ
では、例題で練習してみましょう。
例題:3点(4、9)(7,6)(2,3)を頂点とする三角形の面積を求めよ。

ここで疑問に思った方がいるかもしれません。

にゃんこ
どの点の座標を選んで引いても答えは同じになりますか?

坂田先生
はい、同じです。
例えばさっきの例題において、緑の点の座標を引いても答えは以下のように7となります。


にゃんこ
さて、ここまで解いて、感覚をつかむことができてから、最初に紹介した『原点を通らない3点を頂点とする三角形の面積を求める公式』の解説図を見ると意味がわかりやすいです。


にゃんこ
いきなり、最初からこんな説明を見るとわかりにくいですよね。

坂田先生
この公式に限らず、数学のテキストなんかには、いきなり抽象的な(一般化した)説明から始まっていて意味がわからないことがよくあります。

にゃんこ
そんなときは、今回のように、具体的に数値を代入して計算してみて、感覚をつかめてから公式を見るとわかりやすいことが多いです。
合わせて学習したい一次関数
参考:2点から等距離にある直線の式の求め方2通りと公式3つ
参考:3点から等距離にある点の座標の求め方3通り
参考:線分の垂直二等分線の方程式の求め方2通りと公式

































絶対値の記号の外し方の練習:絶対値の記号を外す問題:基本~難問