- 等積変形を応用し座標平面上の三角形の面積を求める手順
- 等積変形をグラフ上で利用するバリエーションの練習問題
- 練習問題&解き方のまとめプリント
次の△ＡＢＣの面積を求めよ。
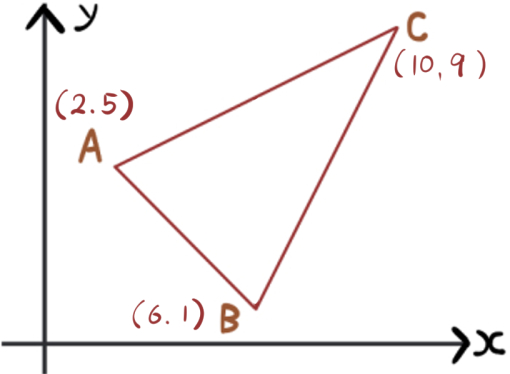
- ２つの三角形に分解してそれぞれの面積を求める
- 等積変形によって三角形の形を変化させてから面積を求める
- 三角形が内接する長方形の面積を求めてから不要な部分を引き算する
- 公式を使う(最終手段)
参考：３点の座標から三角形の面積を求める公式
参考：様々な面積比の求め方の違い｜相似比・角の二等分線など
等積変形を応用し座標平面上の三角形の面積を求める手順
先程の問題を等積変形の考え方を使って解いていきます。
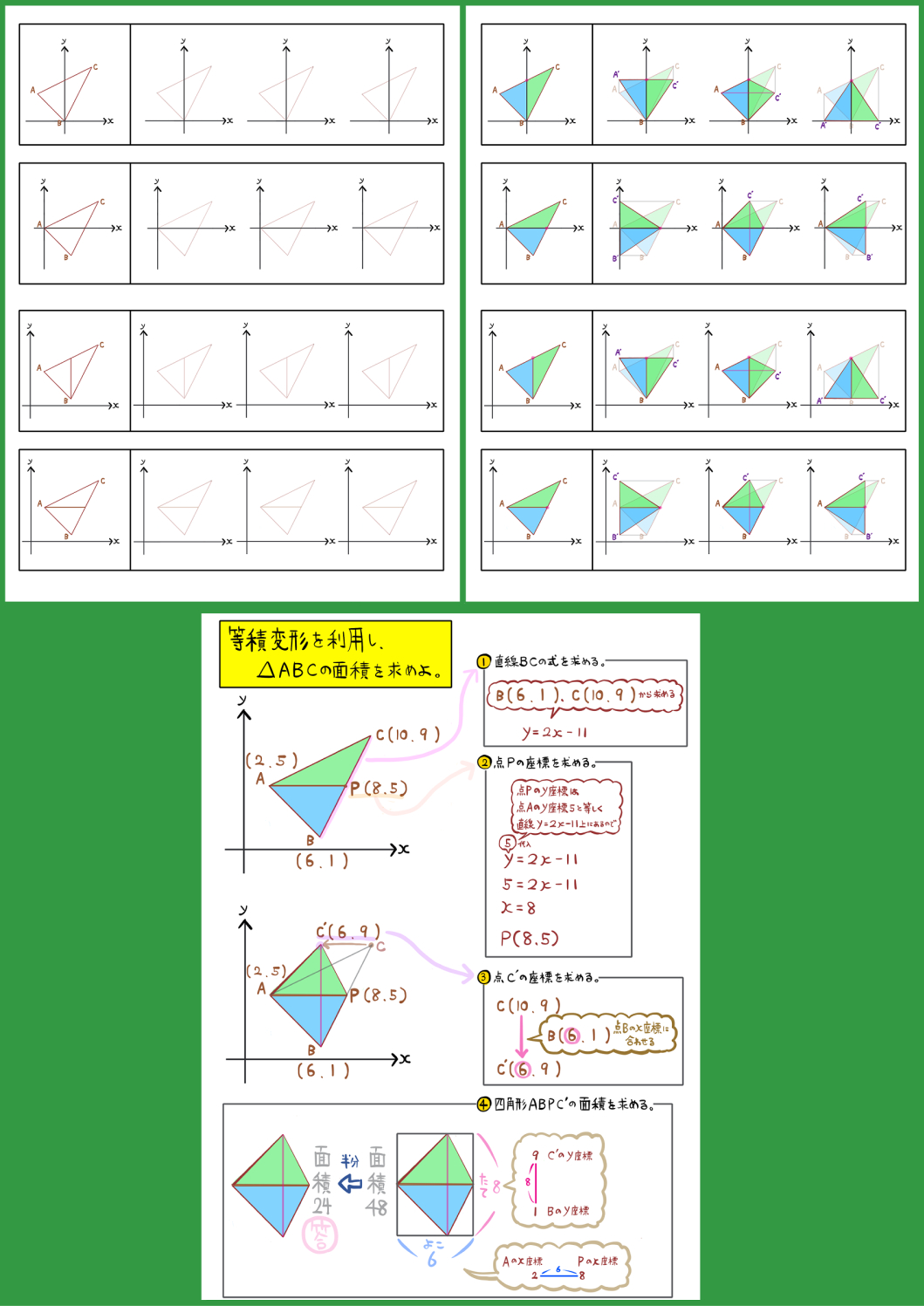
等積変形を利用し、△ＡＢＣの面積を求めよ。
△ＡＢＣを上半分と下半分に分け、上半分だけを等積変形によって頂点Cを平行移動させる。（まだ意味が分からなくても大丈夫です）
まず、下準備として三角形を上下に２つ分けます。
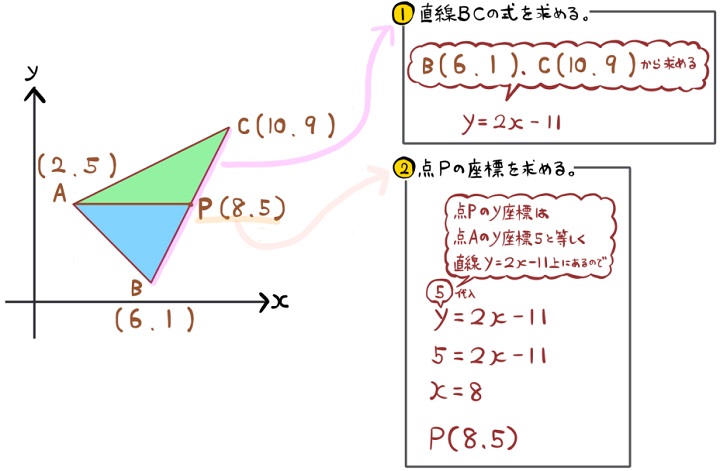
三角形を上下に分けたら、次に、点Pの座標を求めることを考えます。
そのために、手順1、手順2と進めます。
直線BCの式を利用します。
点Pが直線BC上にあることと、点Aと点Pのｙ座標が等しいことを利用します。
直線BCの式に、点Aのｙ座標であるy=5を代入します。
これにより、直線BC上にあってｙ座標が５である点Pのｘ座標を求める方程式を作ったことになります。
これを解いてx=8となり、点Pの座標は(8,5)だと判明します。
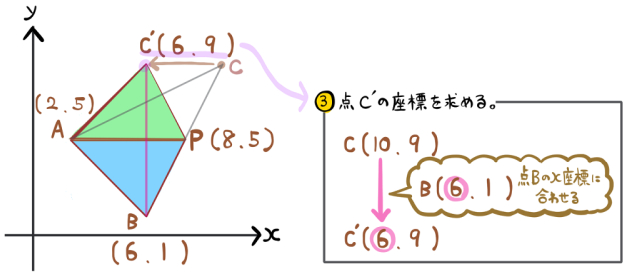図のように点Cを平行移動し、点Bのｘ座標に合わせます。
点Bのｘ座標は６なので、移動後の点C´の座標は(6,9)となります。
△APCの面積と、△APC´の面積は底辺APの長さが同じで高さも同じなので、面積は等しいということになります。（この部分に等積変形の考え方を使っています）
このことにより、△ABCの面積と、四角形ABPC´の面積は同じだとわかります。
つまり、四角形ABPC´の面積を求めると、それがそのまま△ABCの面積だということです。
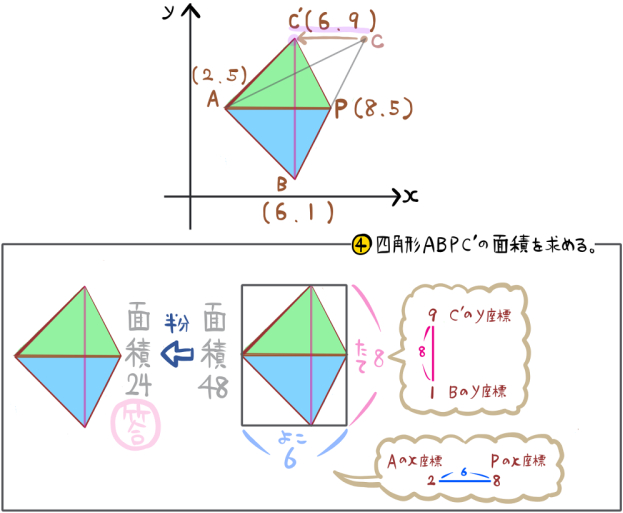図のように、四角形ABPC´の対角線の長さをそれぞれ「たて」と「よこ」とし、その長さを求めます。
たてが８
よこが６
これをかけた４８が、図のように四角形ABPCが内接するような四角形の面積であるということがわかりました。
この半分である２４が求める四角形ABPC´の面積なので、これが答えとなります。
手順２：点Pの座標を求める
手順３：点Cを平行移動し、そのｘ座標を点Bに合わせる。移動後の点C´の座標を求める。手順４：四角形ABPC´の面積を求める。
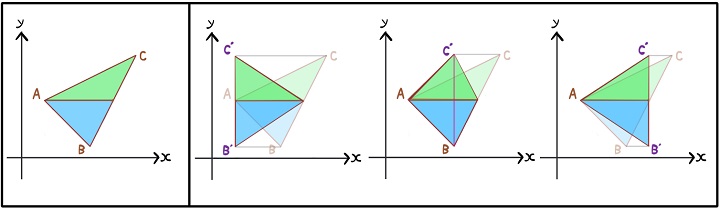（もちろんずらし方は無限に存在しますが、計算しやすい代表的な例をあげています）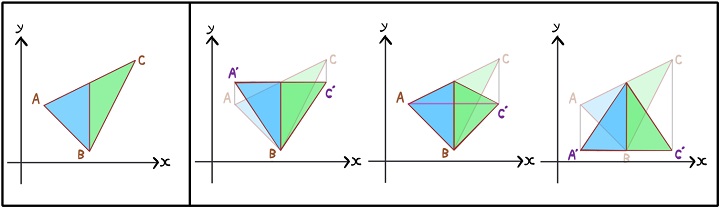
等積変形をグラフ上で利用するバリエーションの練習問題
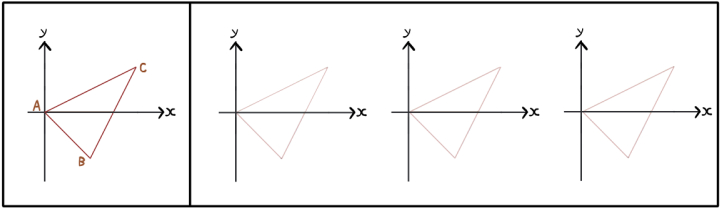
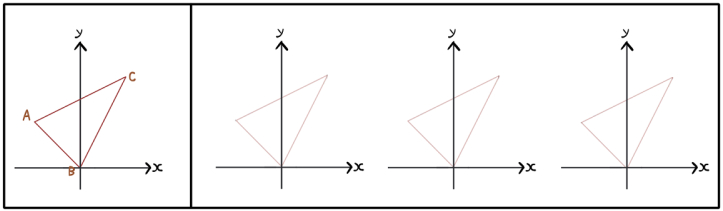これをこのように３パターン変形させる練習をしてください。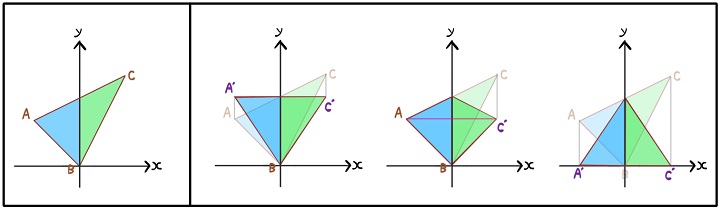
次にこちらのパターンを練習します。
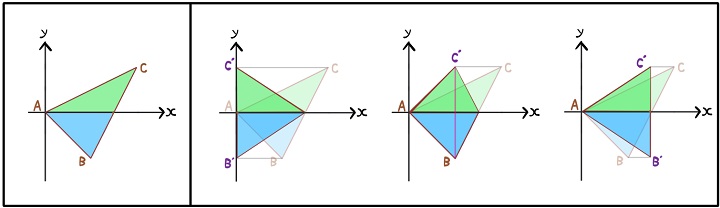
ここまでの２パターンが変形しやすい問題でした。
まずはこの２パターンに慣れましょう。
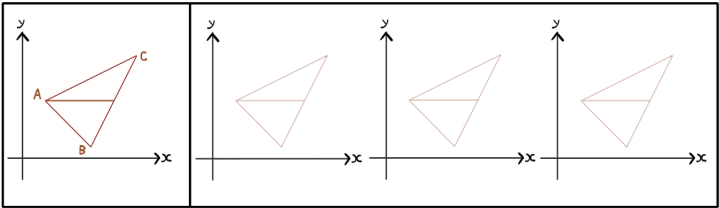
つづいて左右に分けるパターンです。
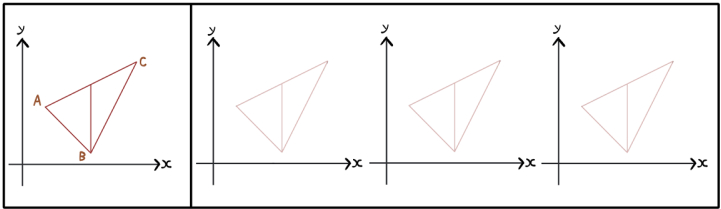
練習問題&解き方のまとめプリント
１：等積変形の練習用プリント（練習したい分をコピーして使ってください）
２：等積変形の解答プリント
３：等積変形を利用し座標平面上の三角形を求める手順まとめプリント
