




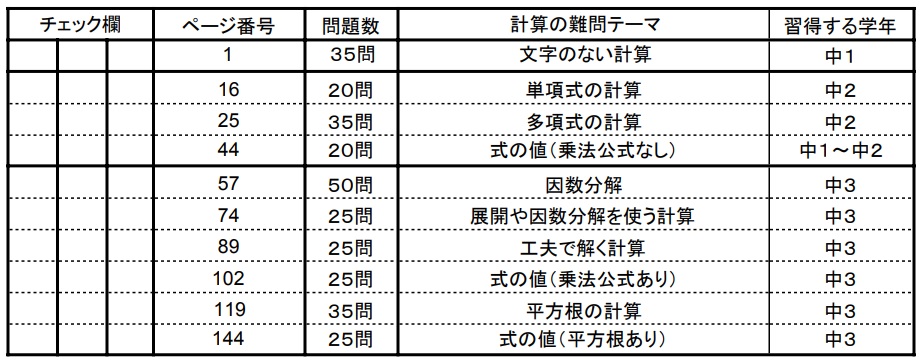
- 中1文字のない計算(正負の数の計算問題・四則演算)
- 中2単項式の計算(単項式の乗除)
- 中2多項式の計算問題の難問
- 中1中2式の値(乗法公式なし)
- 中3因数分解の難問
- 中3展開や因数分解を使う計算(多項式の計算)
- 中3工夫で解く計算問題
- 中3式の値(乗法公式あり)
- 中3平方根の計算問題の難問
- 中3式の値(平方根あり)










高校入試の計算問題の難問シリーズ|学年別&テーマ別


▶学習ページはこちら
高校入試対策のために中1数学の範囲で習得しておくべき計算問題の難問は『正負の数の四則演算』です。中1の範囲と言えど、難関の入試になるほど、この分野からも難しい問題が出題されています。

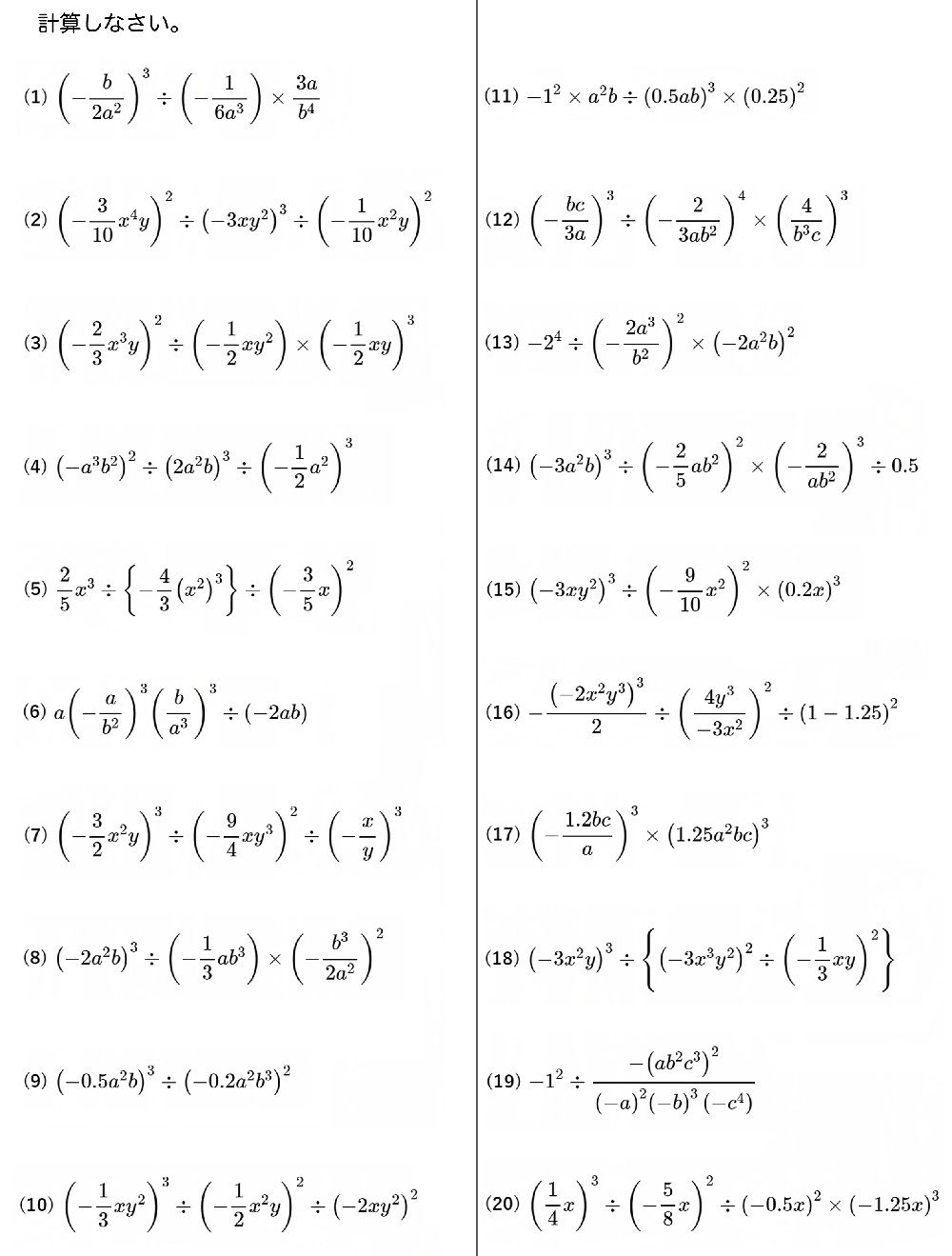
中学2年生で学習する単項式の乗除の難問です。指数法則をふんだんに使いますので、問題が難しくサッパリ解けないと感じたら、まずは単項式の乗除の基礎レベルの問題と、指数法則の基本をまずは鍛えることをおすすめします。


式の値を求める問題は、与えられた条件式をどう利用するか?という応用問題です。中2までに学習する計算力を使って、どのように解答にたどり着くかを習得する分野だと思ってください。有名題だけど知らないと難問となるパターンも掲載しています。


この分野は『このパターンを解いたことがないと気が付きにくい』という問題が多いです。なので、わからないと感じたらすぐに解説を見て、そのあと反復することを重視したほうがいいでしょう。


中3で学習する式の値の問題で、根号のないものをまとめました。乗法公式を学習してからは、式変形のバリエーションが増えます。いきなりここを学習しようとする方は、まずは中2の「式の値」で応用力を付けておくことをおすすめします。
高校入試の計算問題難問をちゃんとマスターするために


- 問題集を最後まで仕上げ、解き方を「理解する」ことが勉強だと思っている。
解き方を理解できた状態というのは、勉強する前の準備が整ったにすぎません。
ここで終わってしまって、反復復習をしないなら、最初から手をつけないほうが良い、ぐらいに思っておくといいでしょう。
これだと、解説を見た時は理解できていたのに、再現しようすると難しいということが起こりやすいです。
身についていない問題にチェックを入れて復習しましょう。
- スラスラ解けるようになっていないのに復習をやめる。「スラスラ解ける」の基準があますぎる。
スラスラ解ける状態になるまで繰り返してね、と伝えるだけでは、ほぼ100パーセント伝わっていないことにある時気が付きました。「ただ解ける状態」と「スラスラ解ける状態」の間には、何倍もの実力差があります。
スラスラというのは、掛け算の九九ドリルを解くときのように、手が追い付かない感覚になっている状態のことを指します。
テスト勉強の時は解けていたけれど、テスト本番では緊張して頭が真っ白になる、という場合はこの状態でのストックが足りないと思ってください。

最もやってはいけない勉強法は、『いろいろな問題集に手をつけて反復しない勉強法』です。

それよりも、今すぐ手元の愛用テキストを反復することに集中してください。
なぜなら反復している時間こそ勉強時間だからです。
反復することで徐々に解き方を自分のものにすることができ、そうなって初めて試験中に道具として使いこなすことができます。
高校入試の計算問題の難問対策として準備しておきたい指数法則


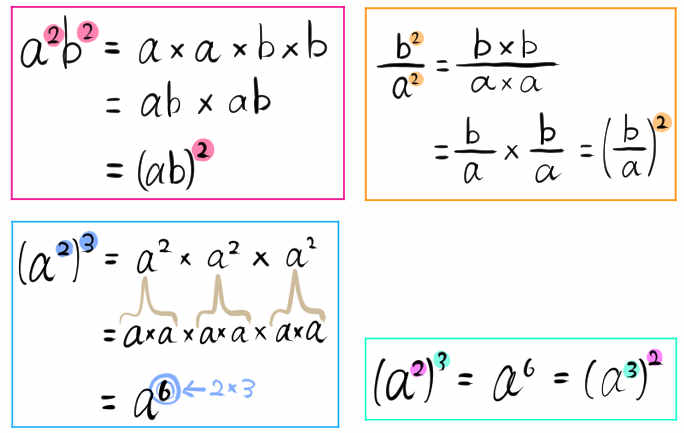

計算しなさい。
\(\dfrac{\left\{ \left( 1+\sqrt{3}\right) ^{50}\right\} ^{2}\left( 2-\sqrt{3}\right) ^{50}}{2^{50}}\)
(立命館高校)



一度理解できたら、慣れるまで手を動かしましょう。
計算や式変形でまだ慣れない部分があれば、スラスラ解けるようになるまで、手を動かして練習することをおすすめします。(この点は、方程式の文章題の練習方法とは異なります。)
































(各高校の出題傾向によって多少違いますので、過去問のチェックはしておいてください)