

- 2点から等距離にある直線の式の求め方2通り
- 2点から等距離にある直線の式の公式3つ
参考:3点から等距離にある点の座標の求め方3通り
参考:3点を頂点とする三角形の面積を求める公式|原点を通る場合通らない場合
参考:線分の垂直二等分線の方程式の求め方2通りと公式
2点から等距離にある直線の式の求め方2通り


2点\(A(1,2)\),\(B(3,4)\)から等距離にある直線の方程式を求めよ。

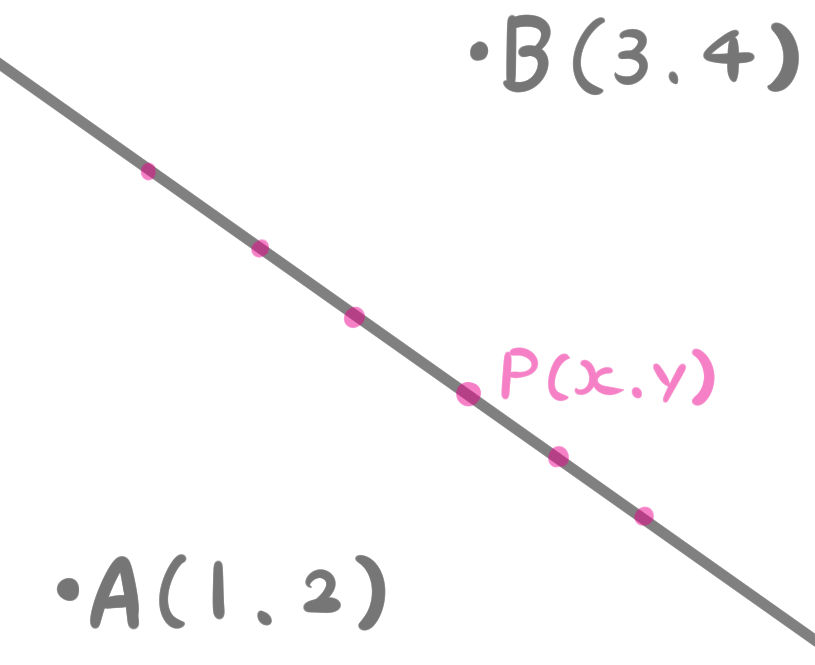


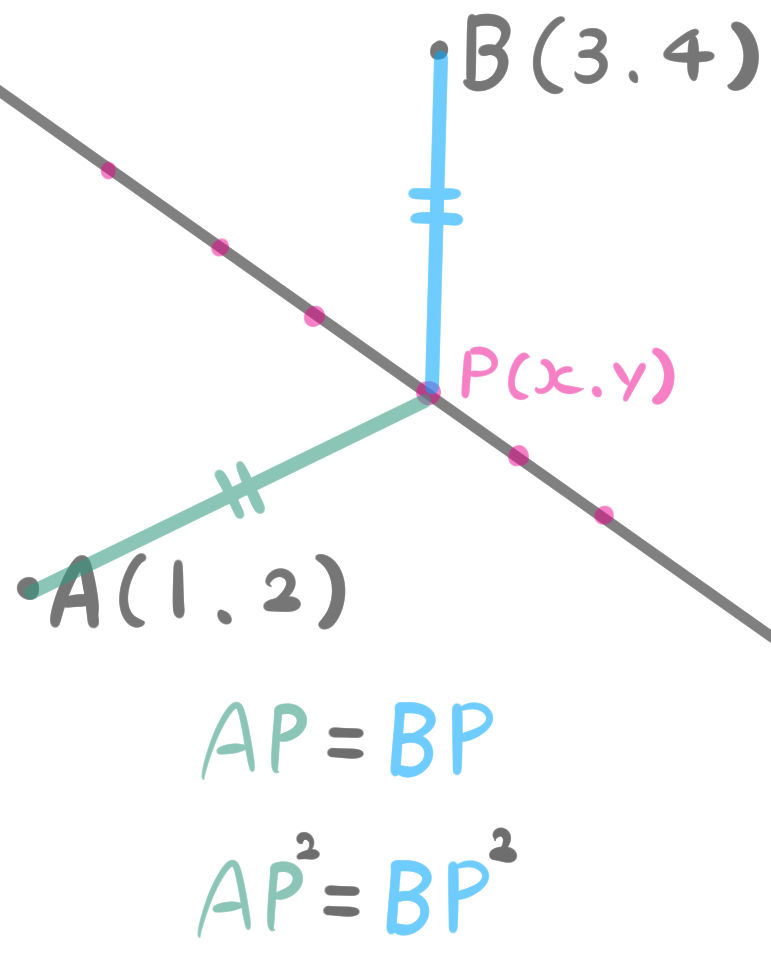







「2点A、Bから同じ距離にある直線」とは、別の言い方をすると「線分ABの垂直二等分線」ということになります。

2点から等距離にある直線の式の公式3つ


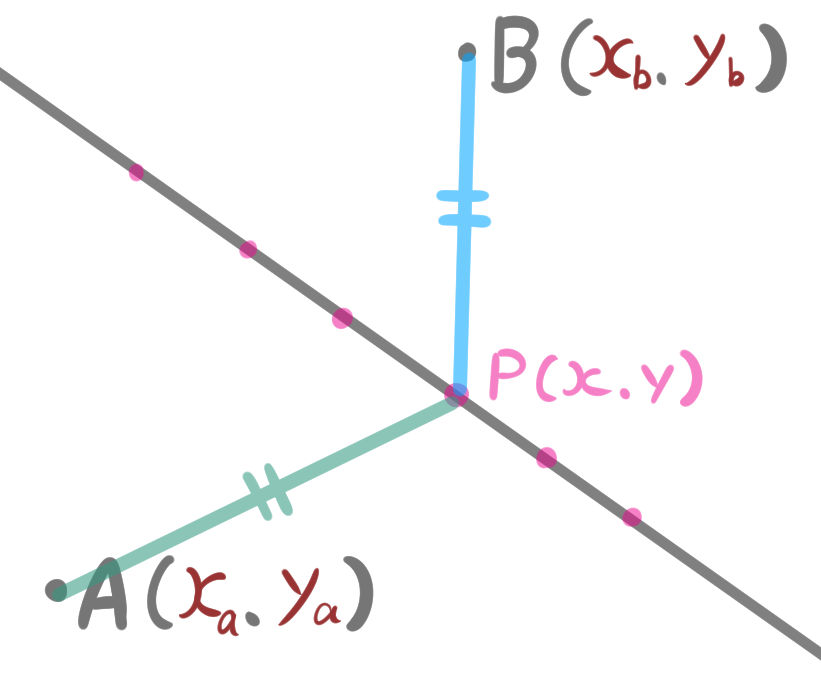


しかし次のように変換するとスッキリします。

このように書き変えるといいでしょう。
ただし、差を求める部分(x座標の差、y座標の差)は、引く順番をそろえる必要があります。(次のように)
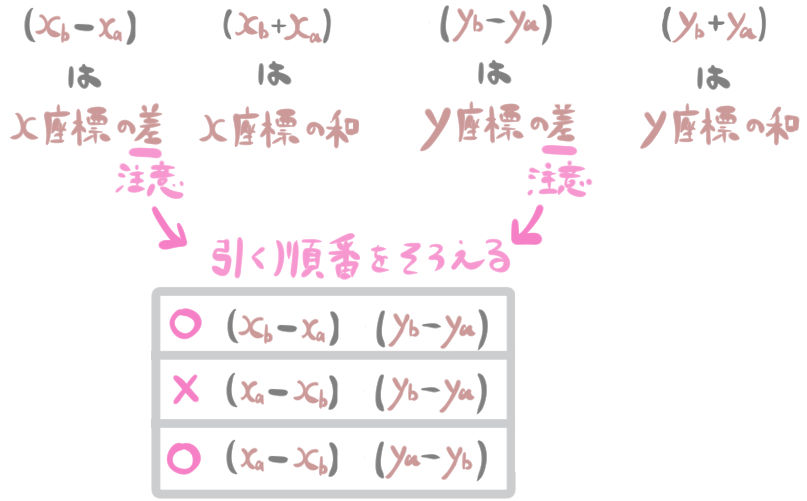
このように、x座標の差を求める時に
点Bのx座標-点Aのx座標
というようにしたなら、y座標の差は
点Bのy座標-点Aのy座標
をしなければいけません。
(点Aのy座標-点Bのy座標をしてはいけません。)
逆に、x座標の差を求める時に
点Aのx座標-点Bのx座標
というようにしたなら、y座標の差は
点Aのy座標-点Bのy座標
をしなければいけません。
(点Bのy座標-点Aのy座標をしてはいけません。)



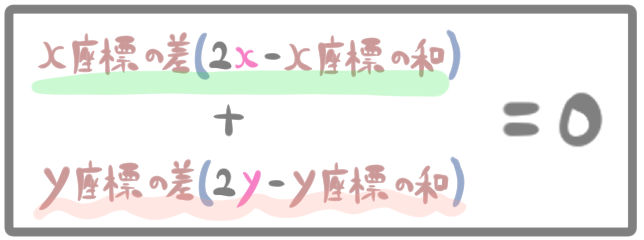

一次関数の基本形で表した公式です。



2点から等距離にある直線の傾きと切片
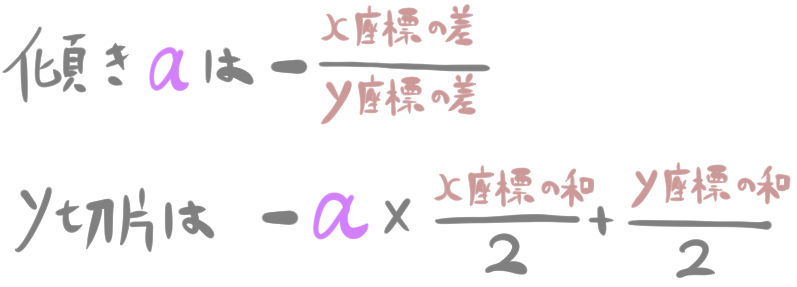
2点から等距離にある直線の公式



x座標の中点←(2点のx座標の和÷2)
y座標の中点←(2点のy座標の和÷2)


「2点A、Bから等距離にある直線の傾き」とはすなわち「直線ABと垂直な傾き」でもあります。
【ポイント】2直線が垂直に交わる時、その2直線の傾きの積は常に\(-1\)となる。

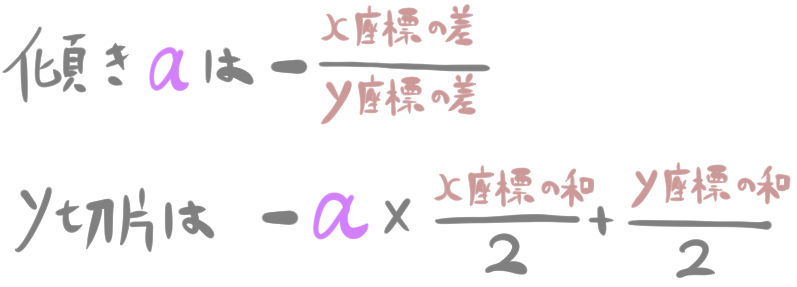


手順2:その直線が2点A、Bの中点を通ることを利用して、x座標の中点の値を変数xに代入し、y座標の中点の値を変数yに代入して、y切片bを求める。

参考:3点から等距離にある点の座標の求め方3通り
参考:3点を頂点とする三角形の面積を求める公式|原点を通る場合通らない場合
参考:線分の垂直二等分線の方程式の求め方2通りと公式


























\(x\),\(y\)は求める直線上にある変数であり、常にAPとBPの距離が等しいという問題の条件を満たします。
なので、\(y=-x+5\)は求める直線の式を表しているということです。