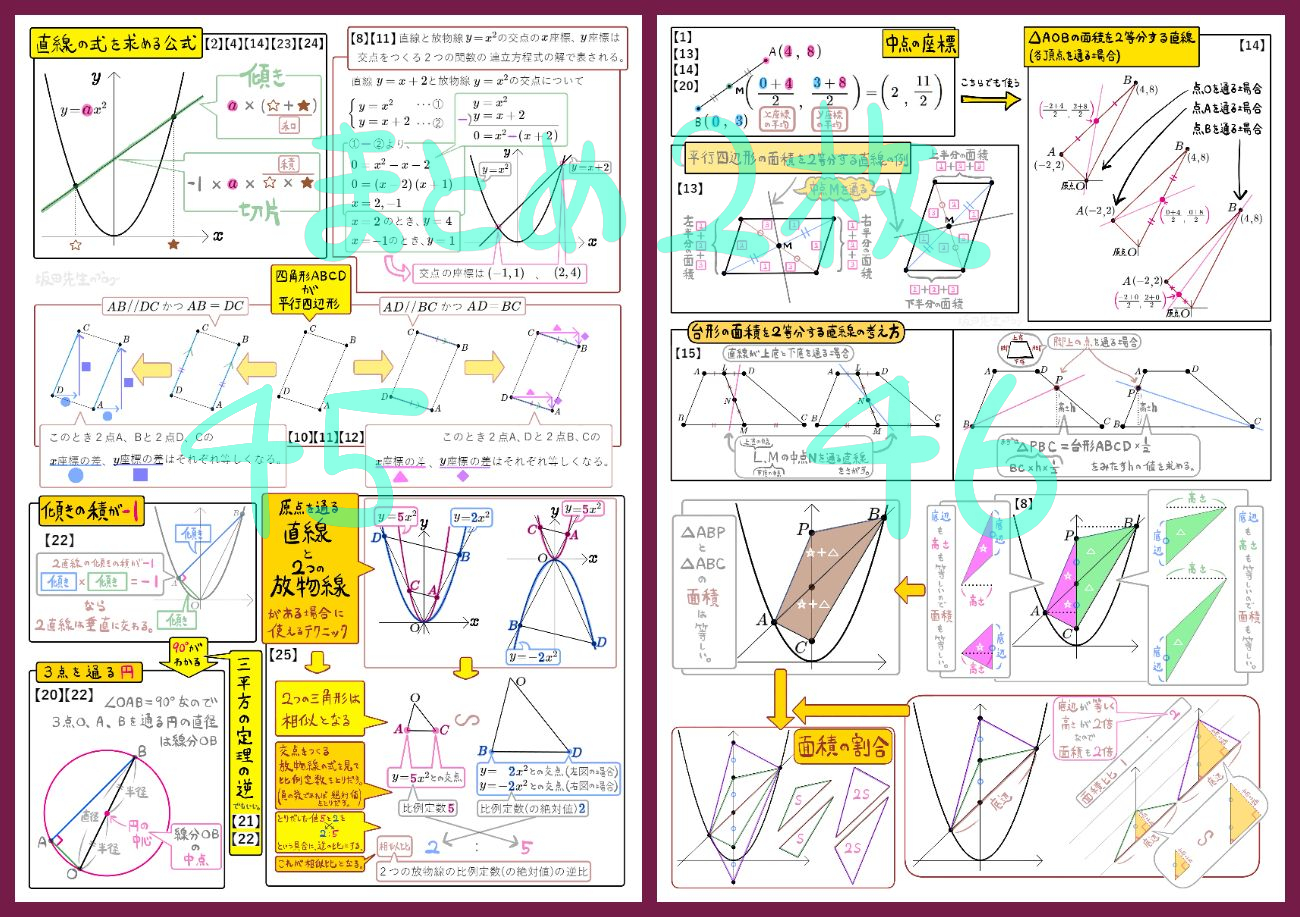
- 高校入試『関数の応用問題』を解く道具の基本セットが身に付きます。
- 計算を短縮できるテクニック集が身に付きます。(後半に一覧あり)












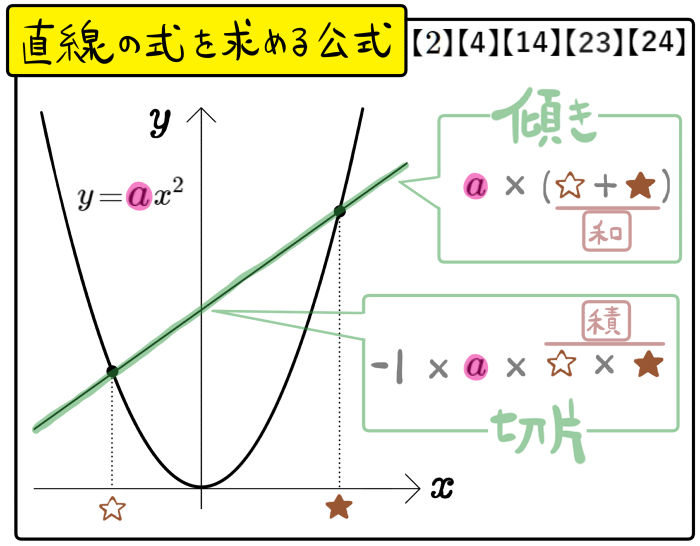
- 2次関数の問題|定期テスト対策用の標準以上のレベル
中学数学の2次関数の定期テストで90点以上を目指す方用の問題です。(教科書やワークの問題をまだ対策していないという方は、そちらを優先することをおすすめします) - 2次関数の難問・応用問題|中学数学~高校入試
定期テストで満点を目指す方用の難問です。当然、高校入試の難問対策も兼ねています。(相似、円周角の定理、三平方の定理といったテーマを除外した問題です。) - 2次関数の標準~難問|融合問題など高校入試対策用
高校入試の2次関数について、標準から難問レベルまで対策するための土台作りとなります。(相似、面積比、円周角の定理、三平方の定理など、2次関数以降に学習するテーマとの融合問題になっています。) - 【復習用】2次関数の難問対策の土台:公式&テクニック集まとめ
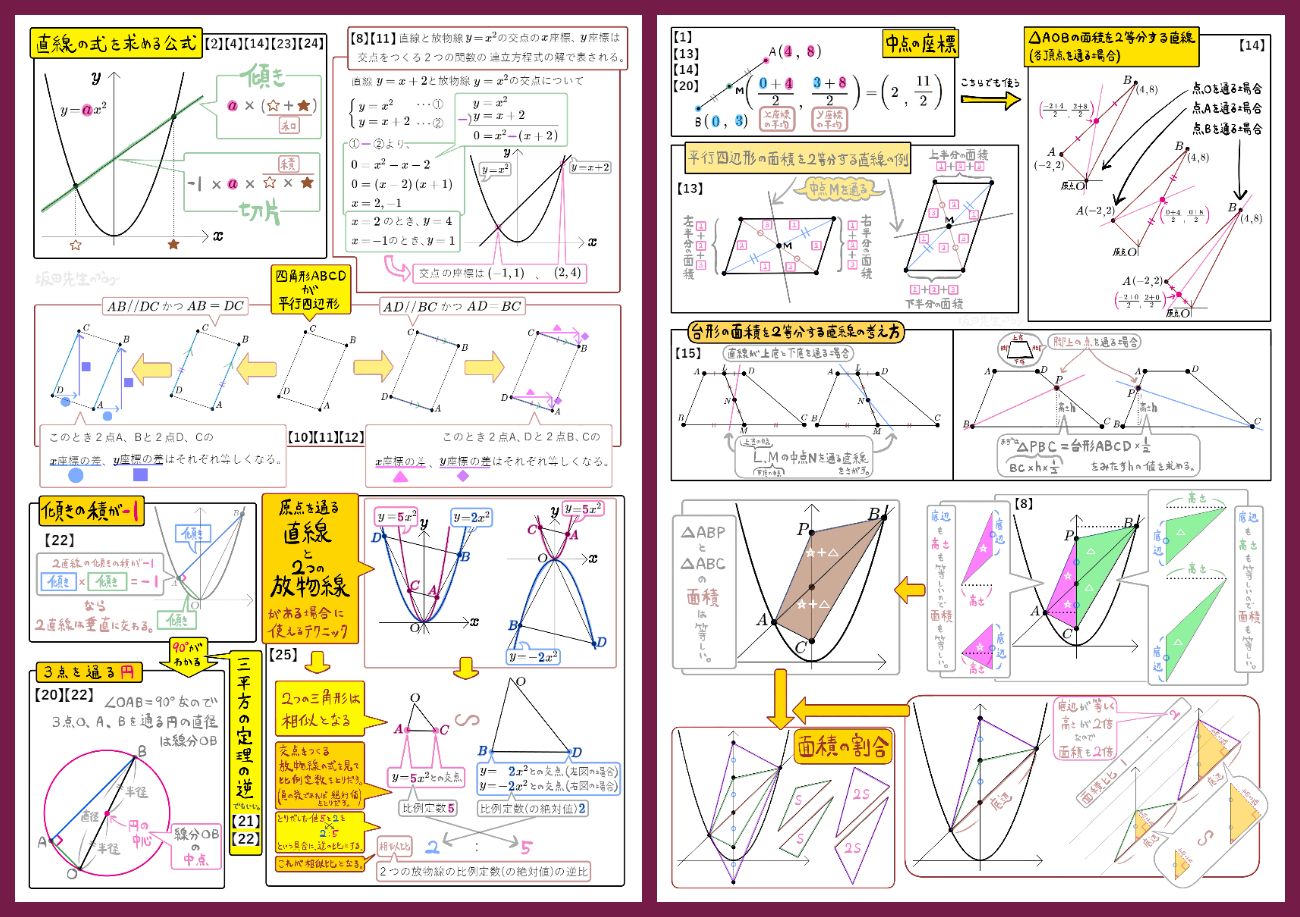
これもプリントアウト版に含まれています。今回の学習で取り扱った「2次関数に関連する公式&テクニック集(まとめ2枚分)」について、一つひとつ復習していきます。









2次関数の問題|定期テスト対策用の標準以上のレベル



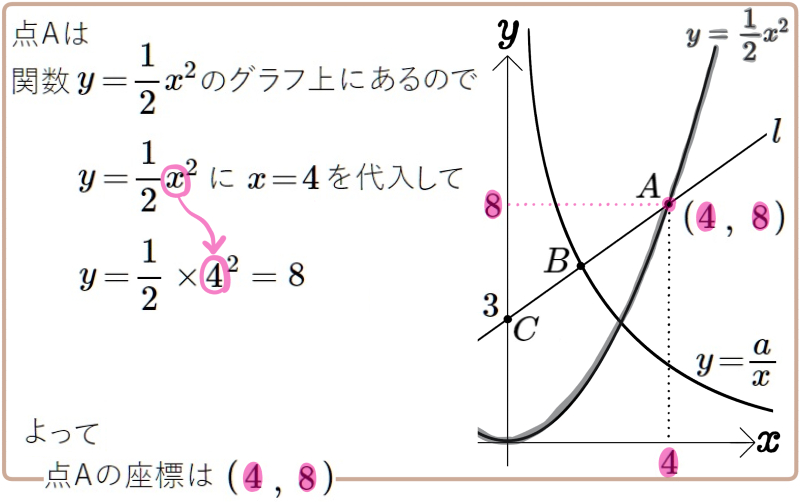
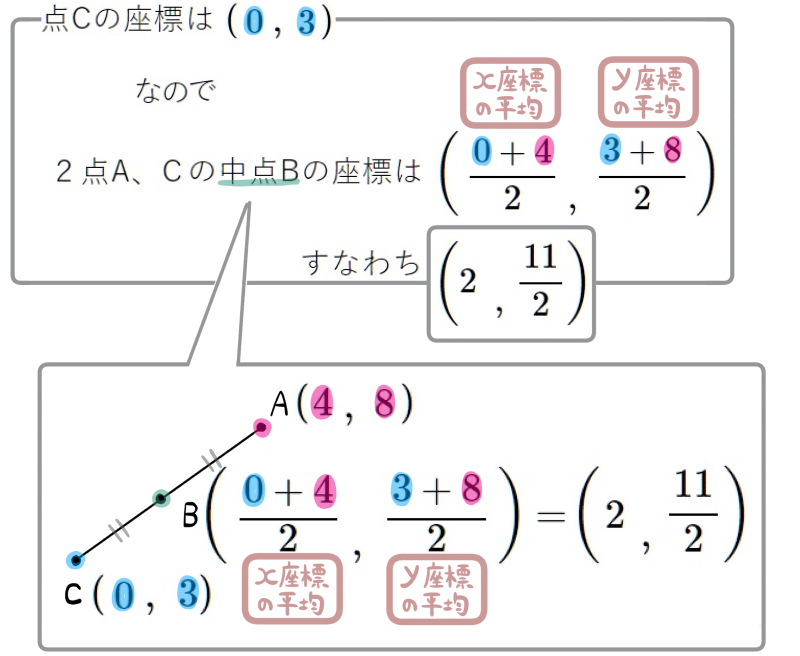
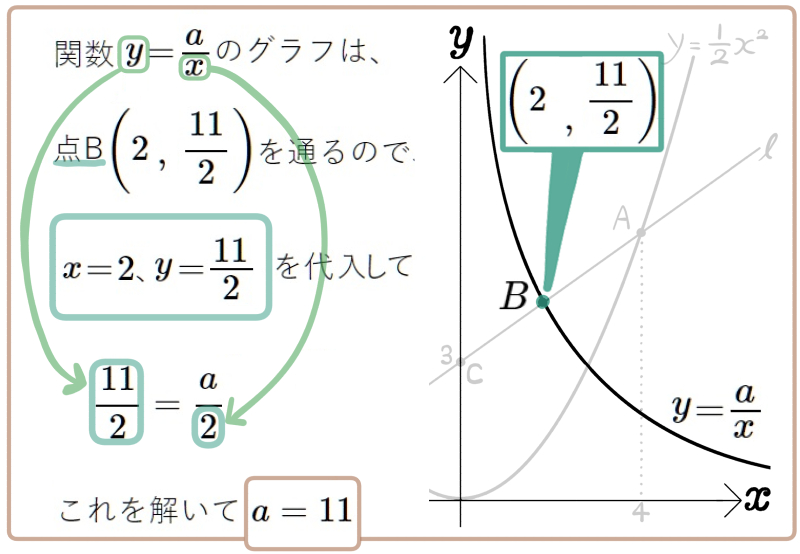
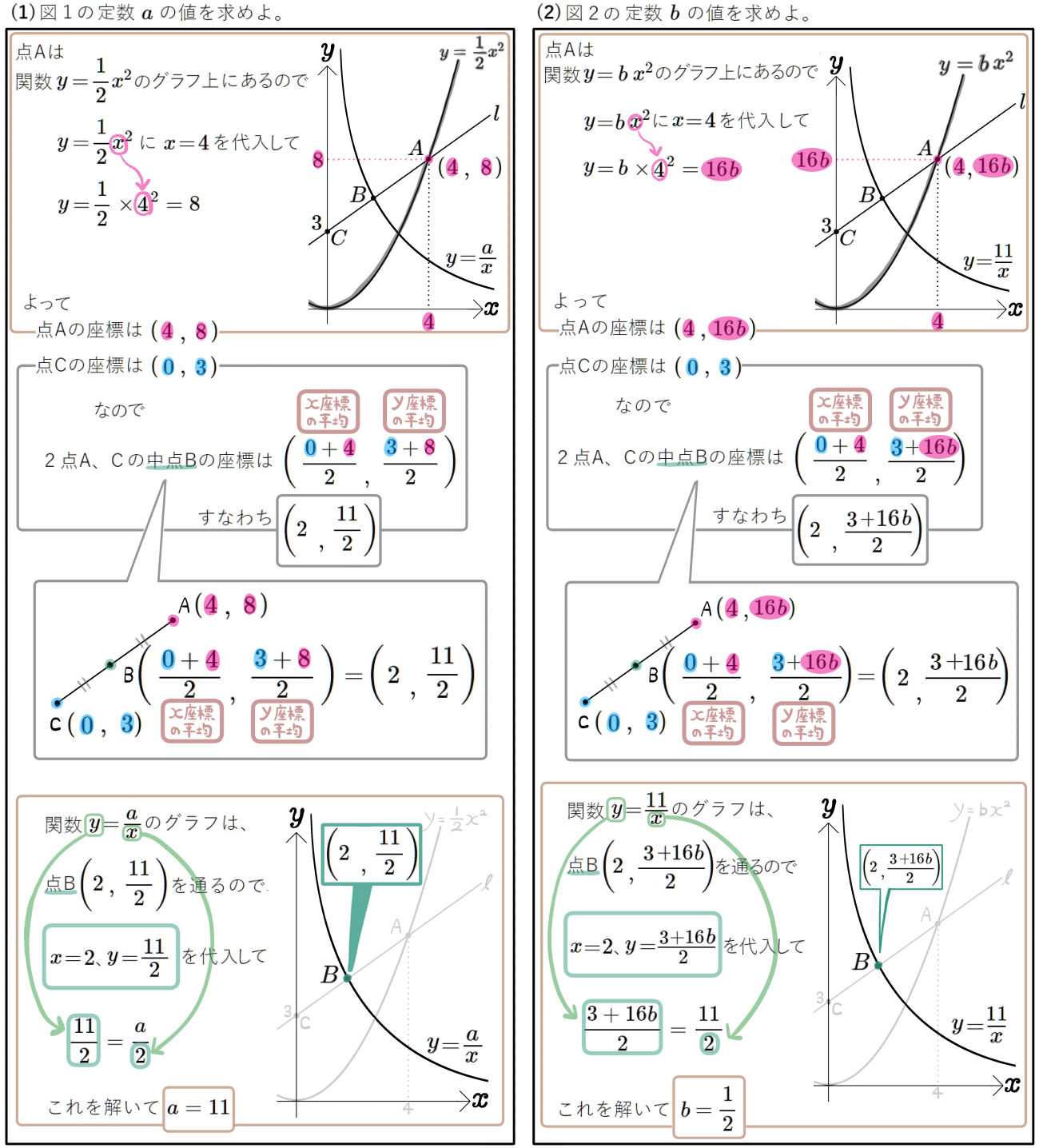
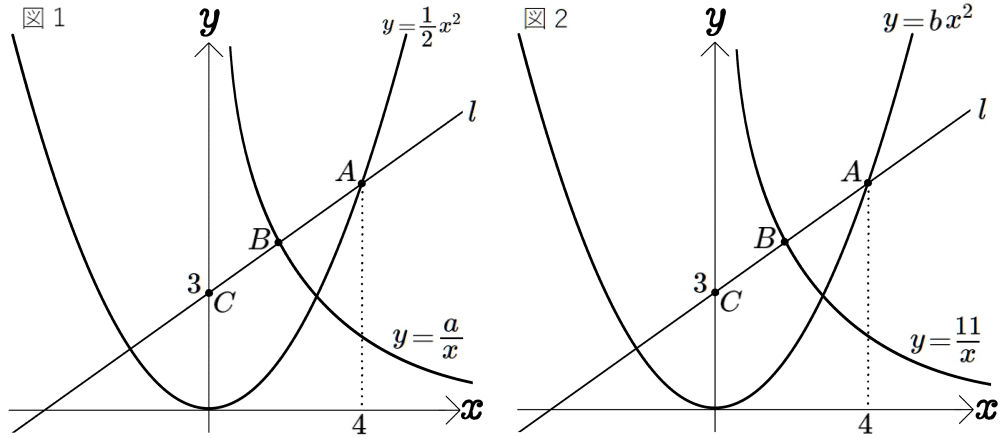 図1図2はともに点Bが、2点A、Cの中点であり、点Aの \(x\)座標は4、点Cの \(y\)座標は3となっている。
図1図2はともに点Bが、2点A、Cの中点であり、点Aの \(x\)座標は4、点Cの \(y\)座標は3となっている。
このとき、次の問いに答えよ。
(1) 図1の定数\(a\) の値を求めよ。

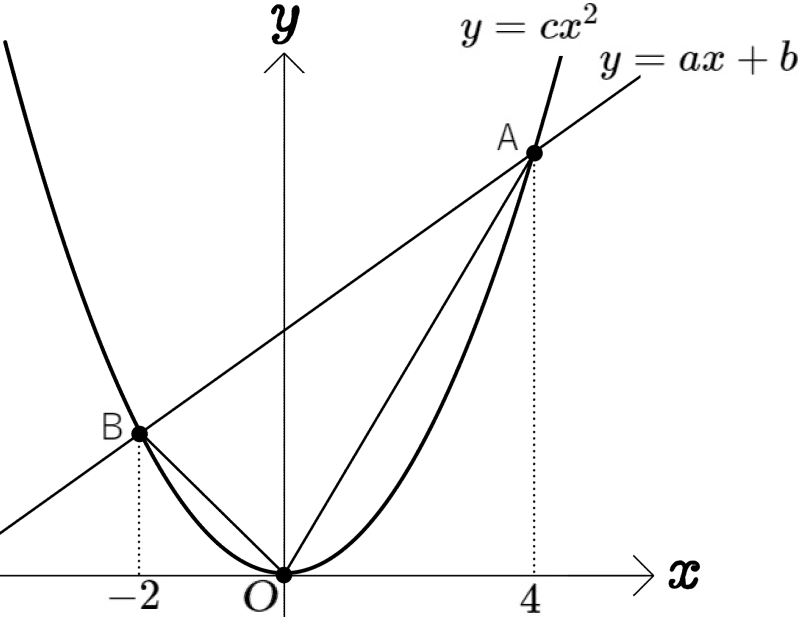 図のように、放物線 \(y=cx^{2}\) 、直線 \(y=ax+b\) があり、その交点Aの \(x\)座標は \(4\) 、交点Bの \(x\)座標は\(-2\) である。△OABの面積が\(18\) のとき、次の問いに答えよ。(\(a\)、\(b\)、\(c\)は定数とする。)
図のように、放物線 \(y=cx^{2}\) 、直線 \(y=ax+b\) があり、その交点Aの \(x\)座標は \(4\) 、交点Bの \(x\)座標は\(-2\) である。△OABの面積が\(18\) のとき、次の問いに答えよ。(\(a\)、\(b\)、\(c\)は定数とする。)
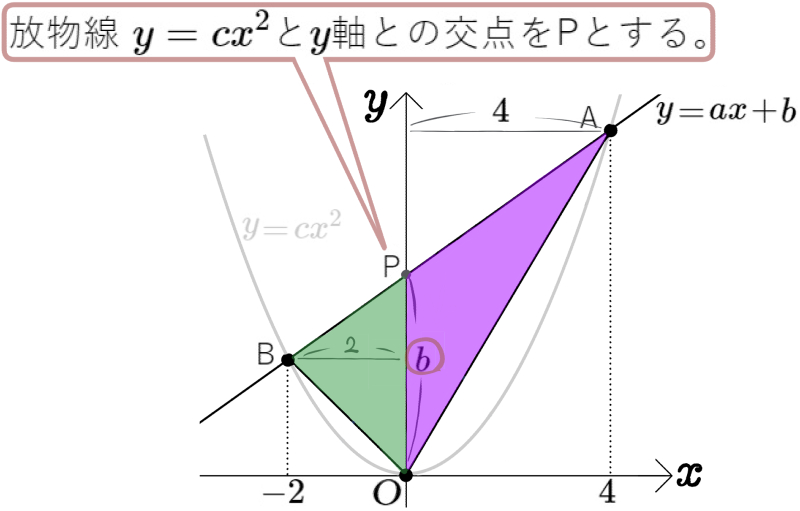
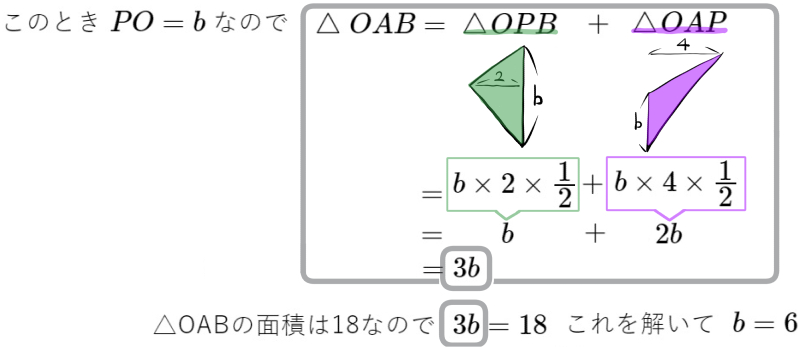
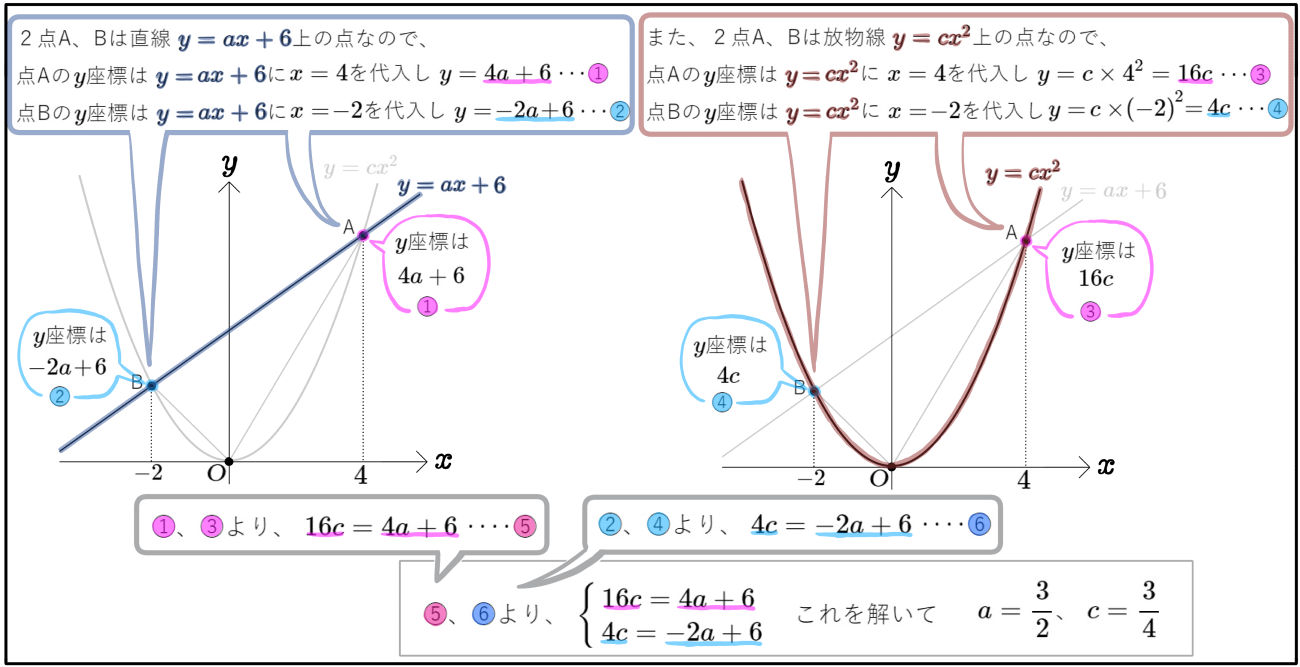
(1) \(b\) の値を求めよ。
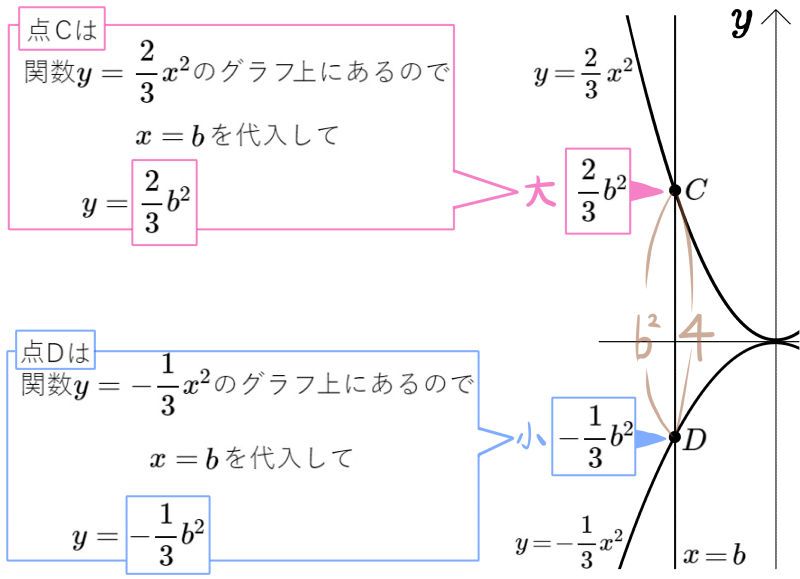
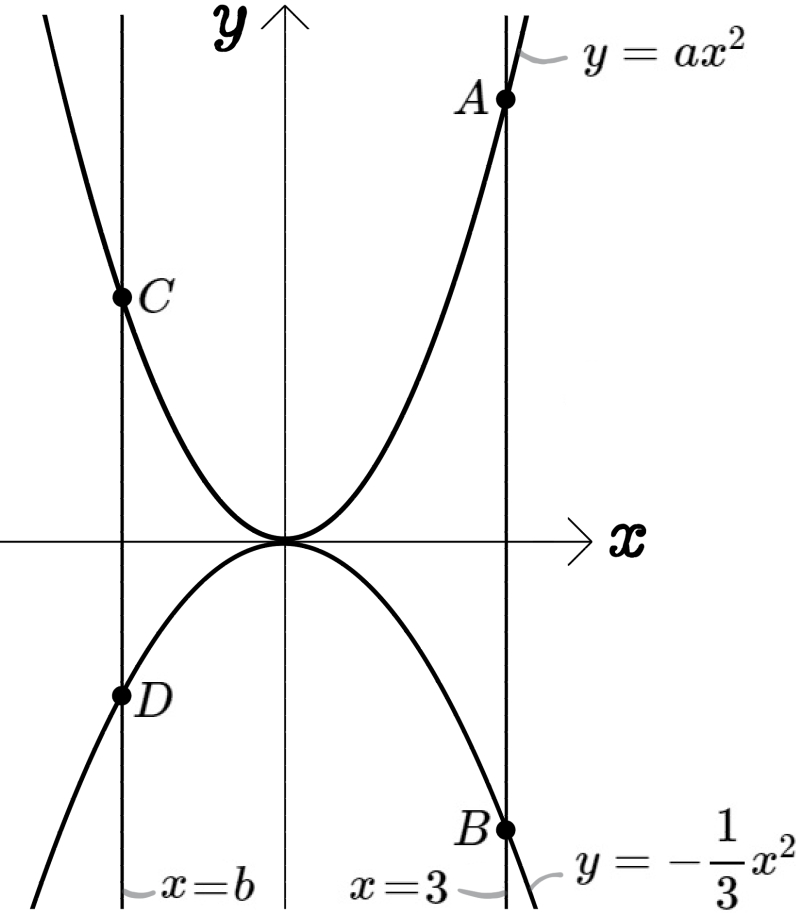 図のように、放物線 \(y=ax^{2}(a>0)\) 、放物線 \(y=-\dfrac{1}{3}x^{2}\) 、直線 \(x=3\) 、直線 \(x=b(b<0)\) がある。(\(a\)、\(b\)は定数とする。)
図のように、放物線 \(y=ax^{2}(a>0)\) 、放物線 \(y=-\dfrac{1}{3}x^{2}\) 、直線 \(x=3\) 、直線 \(x=b(b<0)\) がある。(\(a\)、\(b\)は定数とする。)
放物線と直線との各交点A、B、C、Dを図のように定めるものとする。
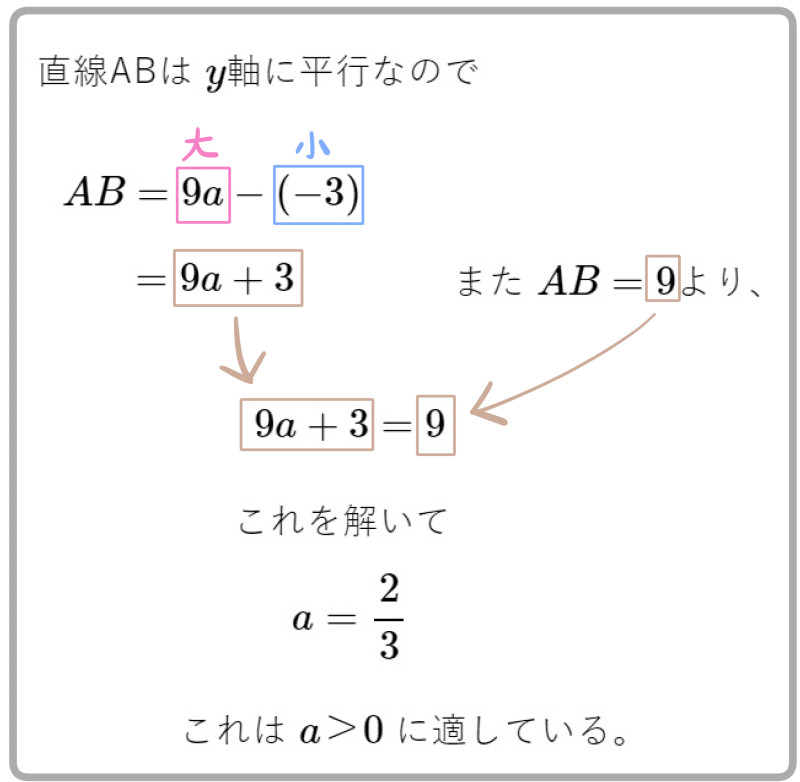
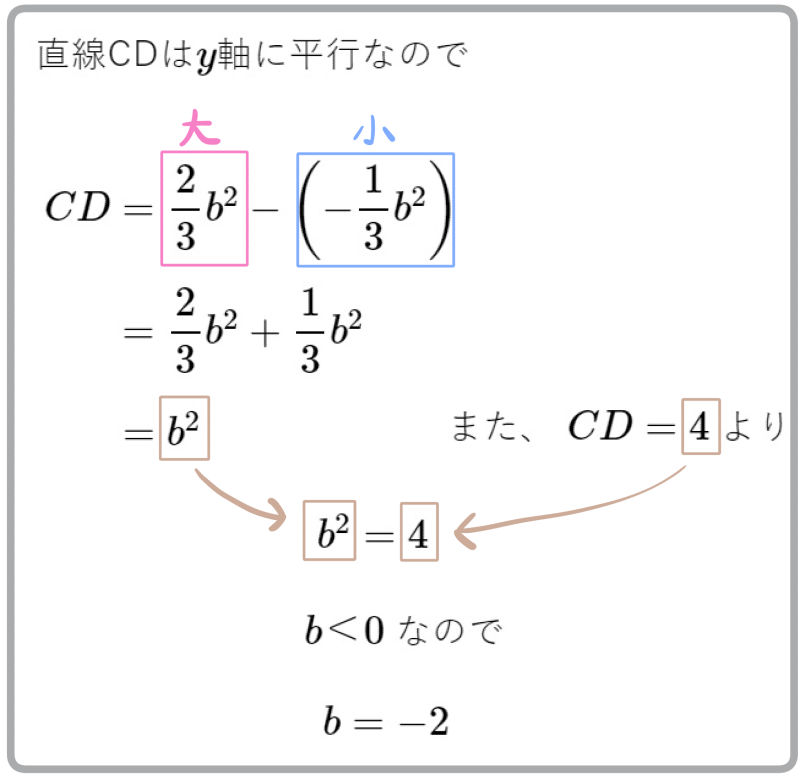
\(AB=9\) 、 \(CD=4\) であるとき次の問いに答えよ。
(1) \(a\) の値を求めよ。
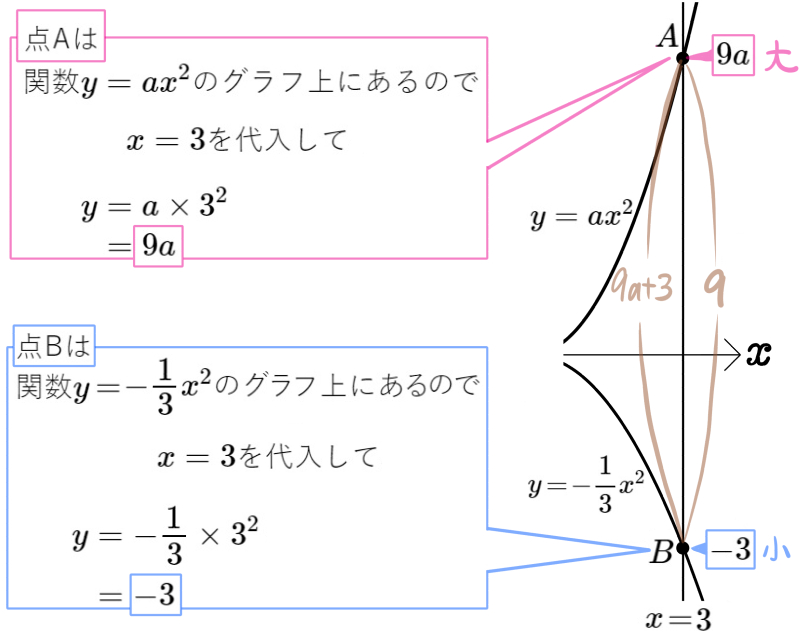
また、y軸に平行な直線の式の表し方を忘れていた方は、直線 \(x=b\)のところで「何これ?」と思ったかもしれません。そんな場合はまず答えを見て、bの値を代入した式を作ってから、もう一度問題を読んでください。
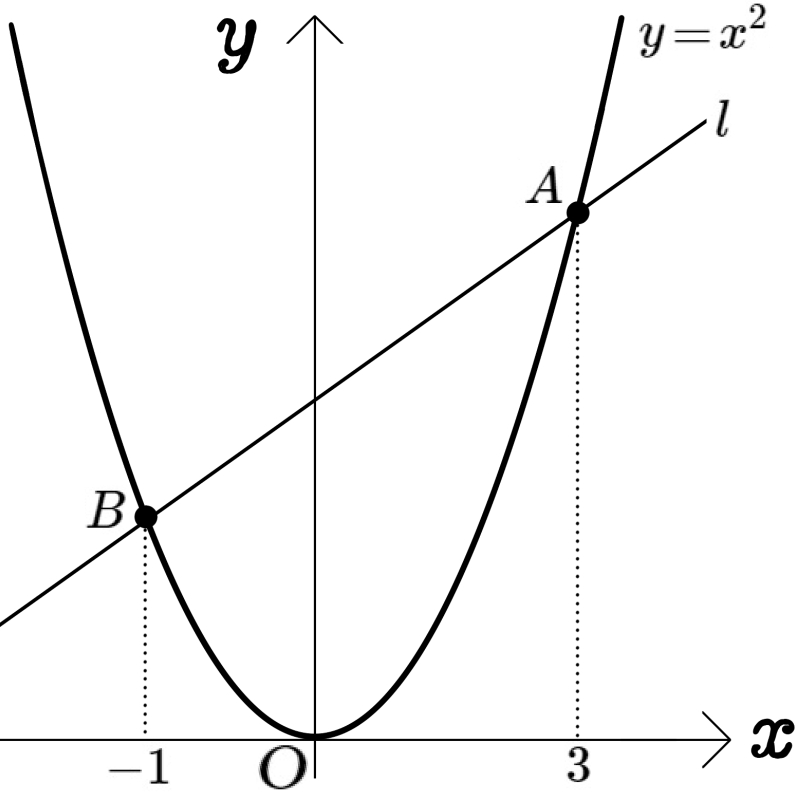 図のように、放物線 \(y=x^{2}\) 、直線 \(l\)があり、その交点をA、Bとする。2点A、Bの \(x\)座標はそれぞれ\(3\)、\(-1\)である。また、放物線\(y=x^{2}\)上に点Pを、直線 \(l\)上に点Qをとり、2点P、Qの \(x\)座標はともに \(t\)であるとする。このとき次の問いに答えよ。
図のように、放物線 \(y=x^{2}\) 、直線 \(l\)があり、その交点をA、Bとする。2点A、Bの \(x\)座標はそれぞれ\(3\)、\(-1\)である。また、放物線\(y=x^{2}\)上に点Pを、直線 \(l\)上に点Qをとり、2点P、Qの \(x\)座標はともに \(t\)であるとする。このとき次の問いに答えよ。
(1)2点P、Qの座標をそれぞれ \(t\)を用いて表せ。
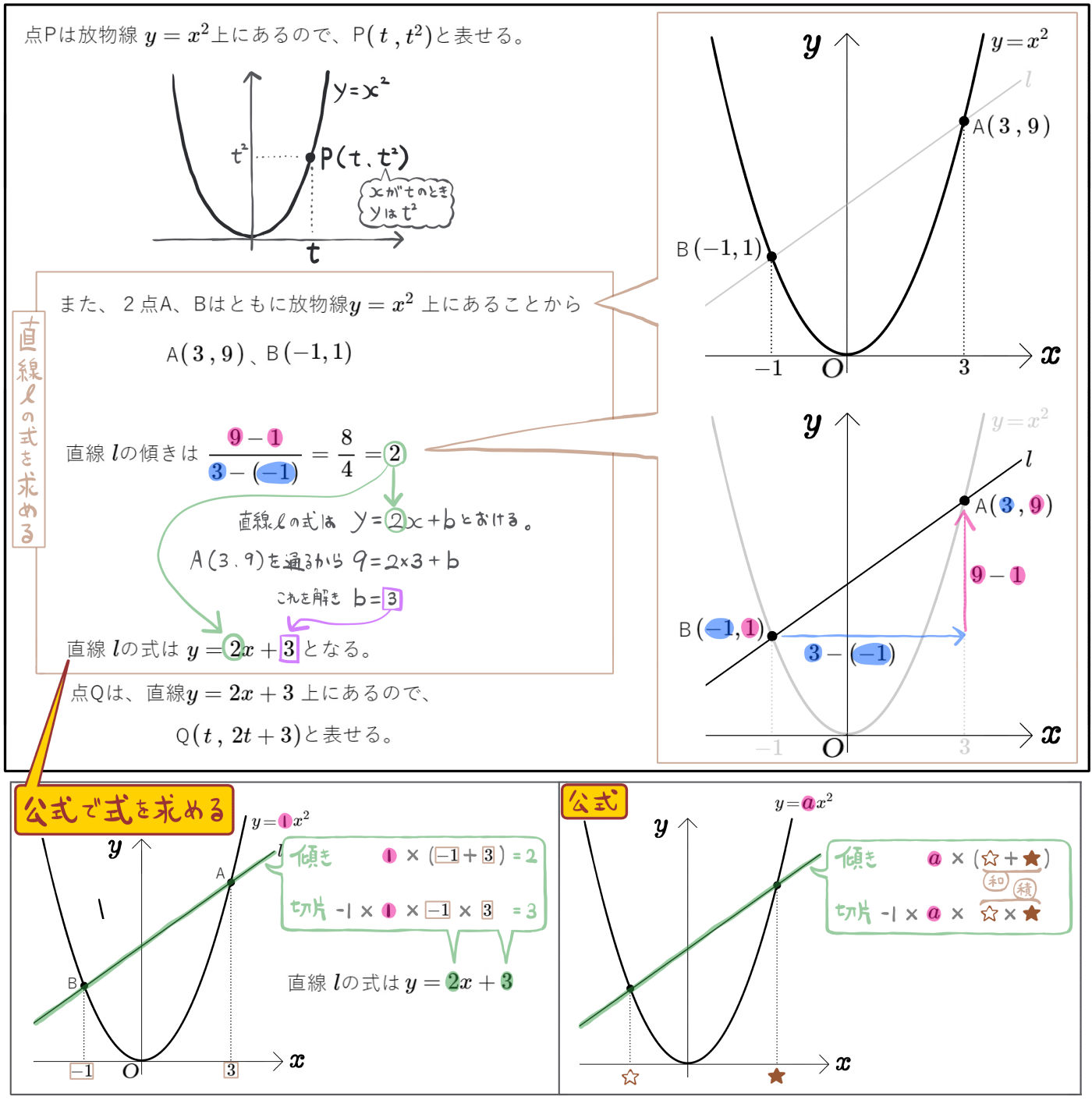 このように、別解として、直線 \(l\)の式を求める際に公式を使う方法もあります。
このように、別解として、直線 \(l\)の式を求める際に公式を使う方法もあります。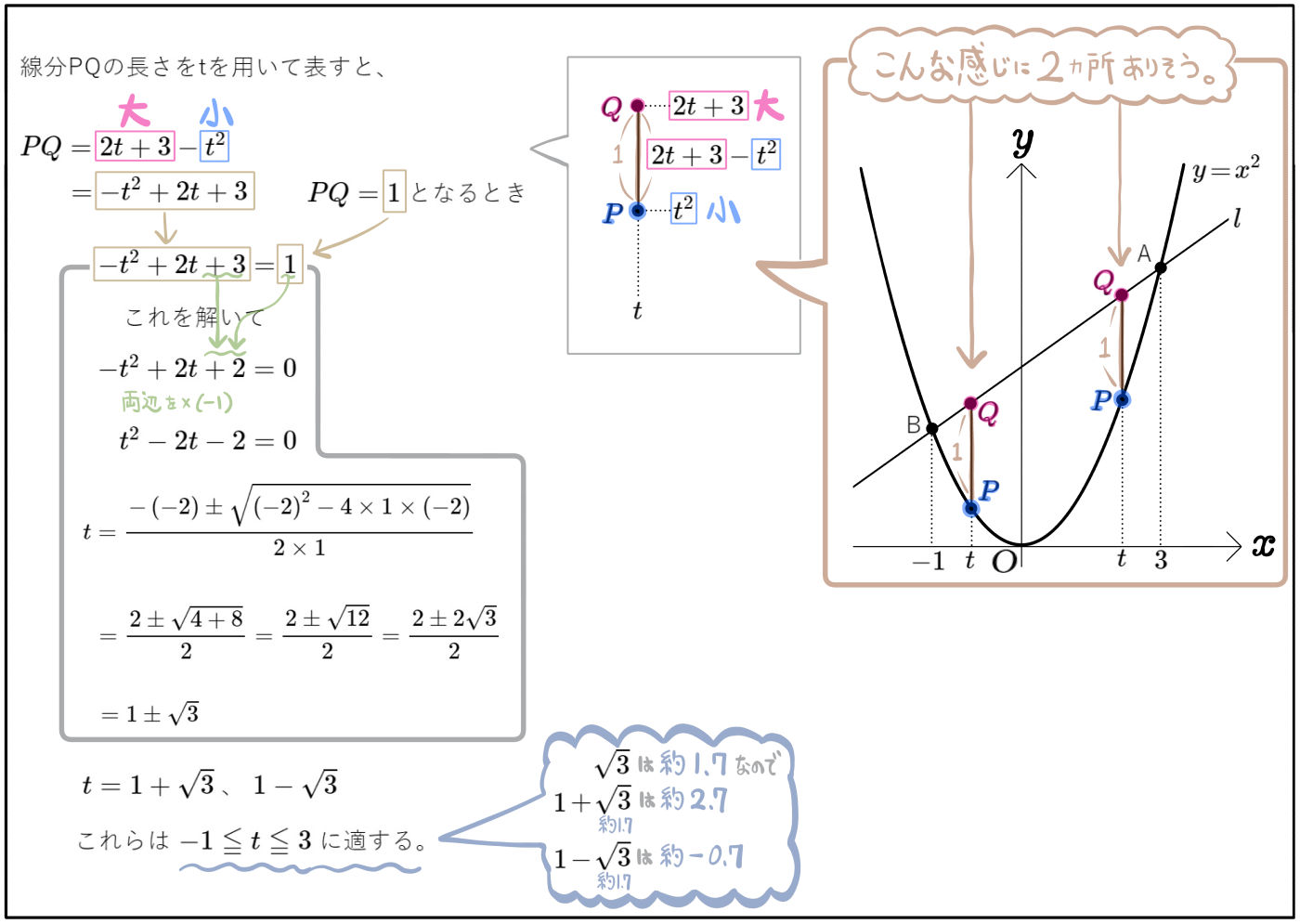
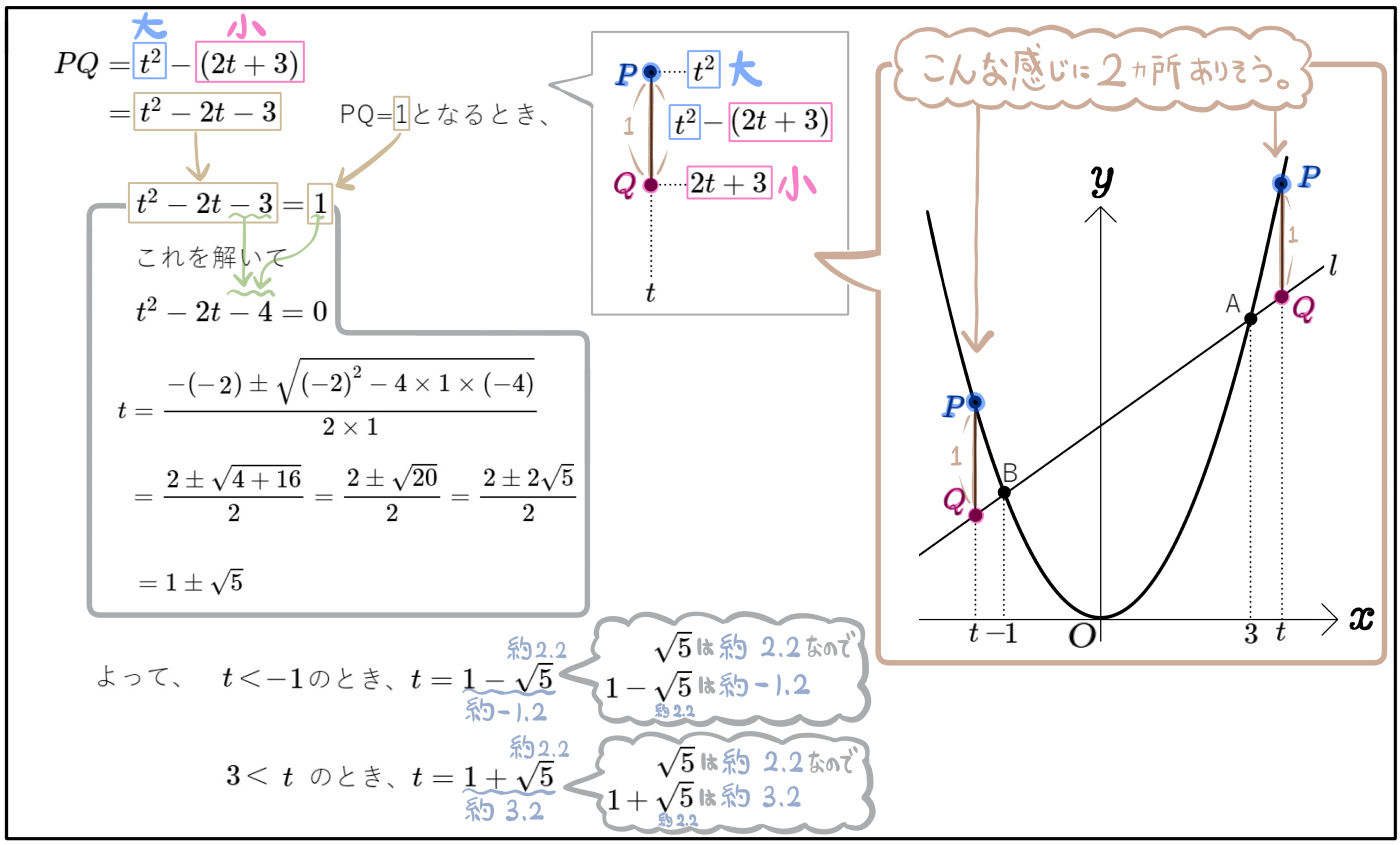
また、(2)(3)の最後に登場したテクニック(\(\sqrt{3}\)や\(\sqrt{5}\)などの近似値を覚えておいて、それを利用して値の大きさをチェックする方法)も知っておいてください。
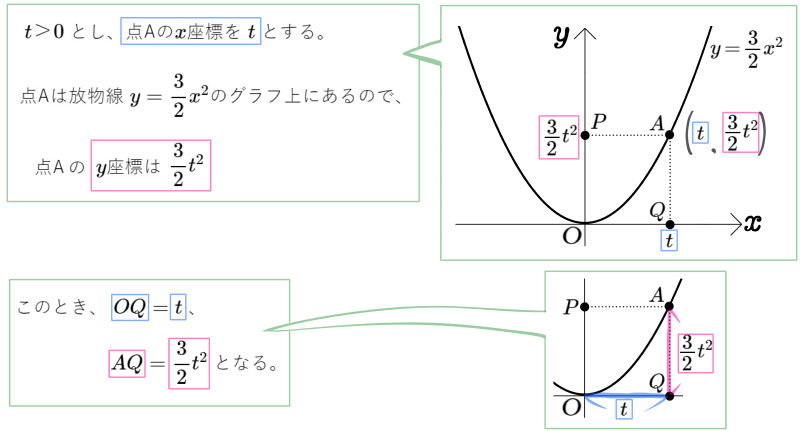
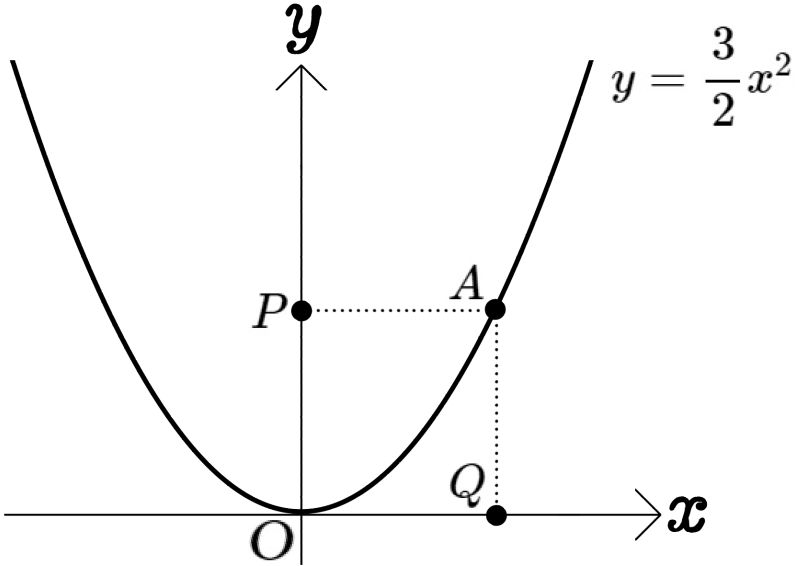 図のように、放物線 \(y=\dfrac{3}{2}x^{2}\)のグラフ上に点Aがある。点Aから\(x\)軸、\(y\)軸に垂線を引き、その交点をそれぞれQ、Pとする。
図のように、放物線 \(y=\dfrac{3}{2}x^{2}\)のグラフ上に点Aがある。点Aから\(x\)軸、\(y\)軸に垂線を引き、その交点をそれぞれQ、Pとする。
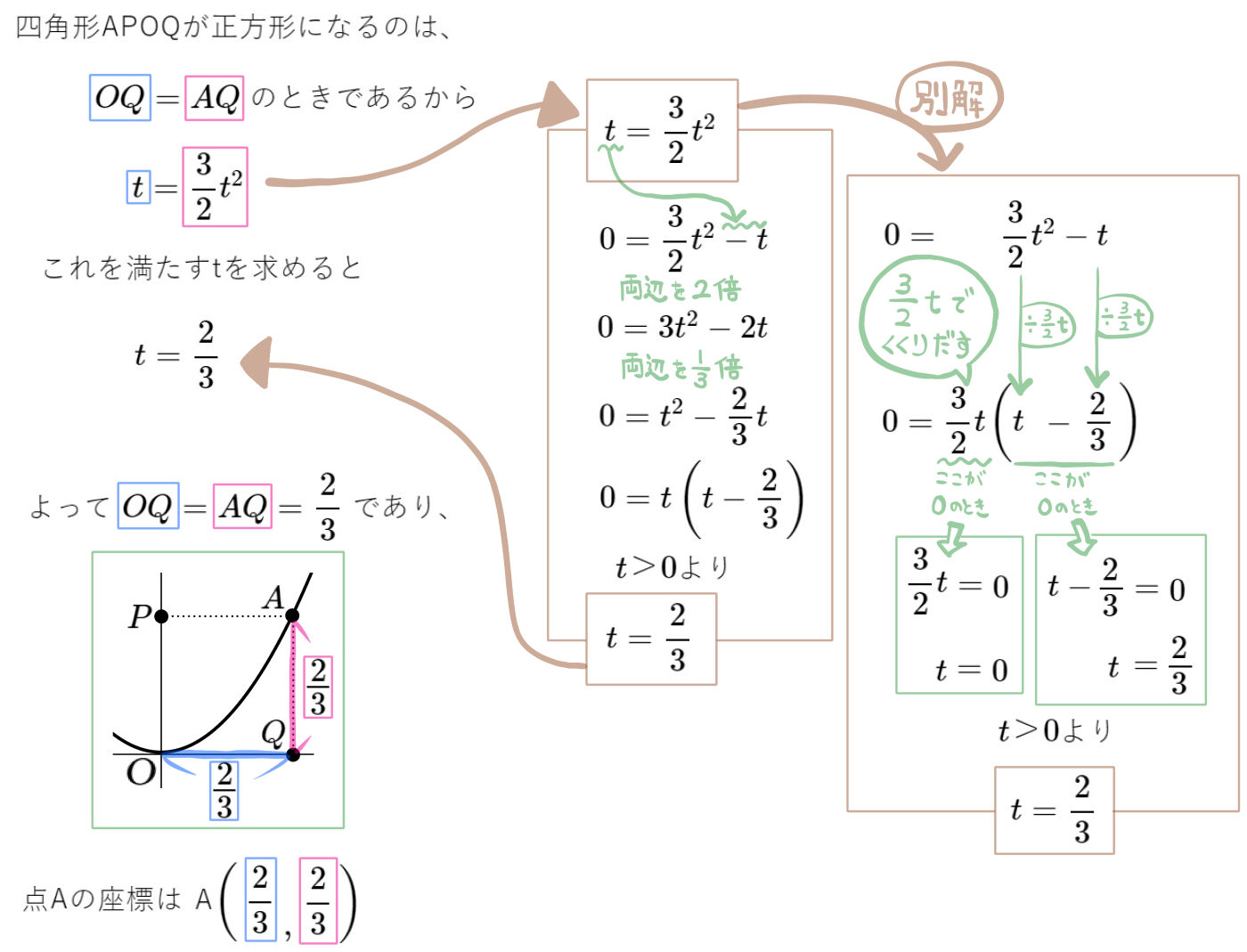
四角形APOQが正方形となるときの点Aの座標を求めよ。ただし、点Aの\(x\)座標は正とする。
\dfrac{2}{3} ,& \dfrac{2}{3}
\end{pmatrix}\)
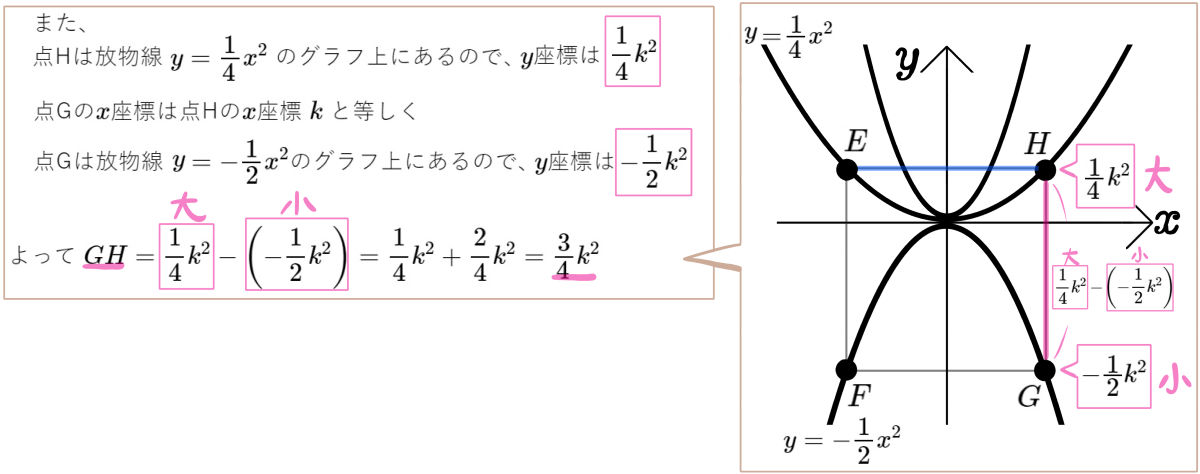
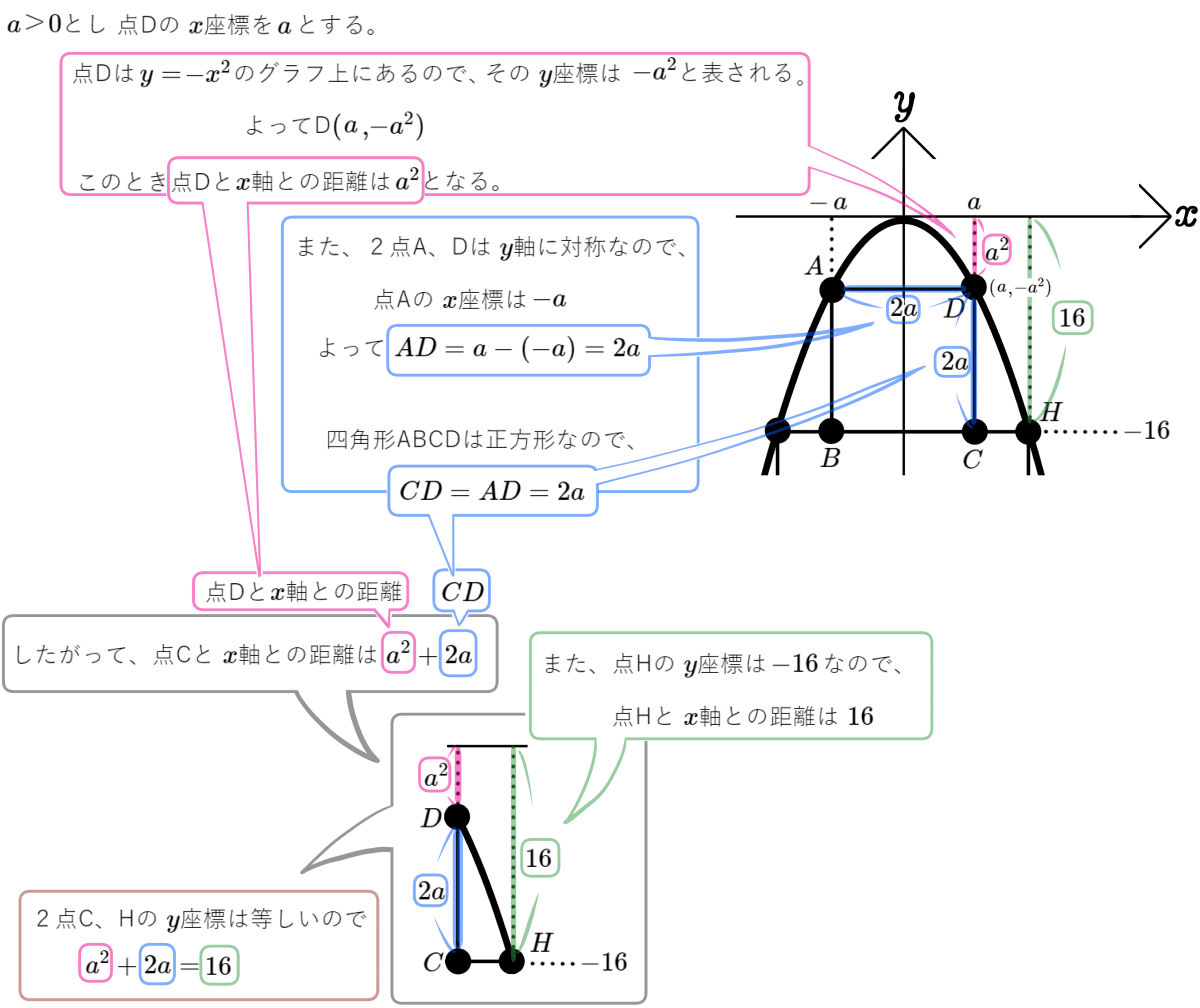
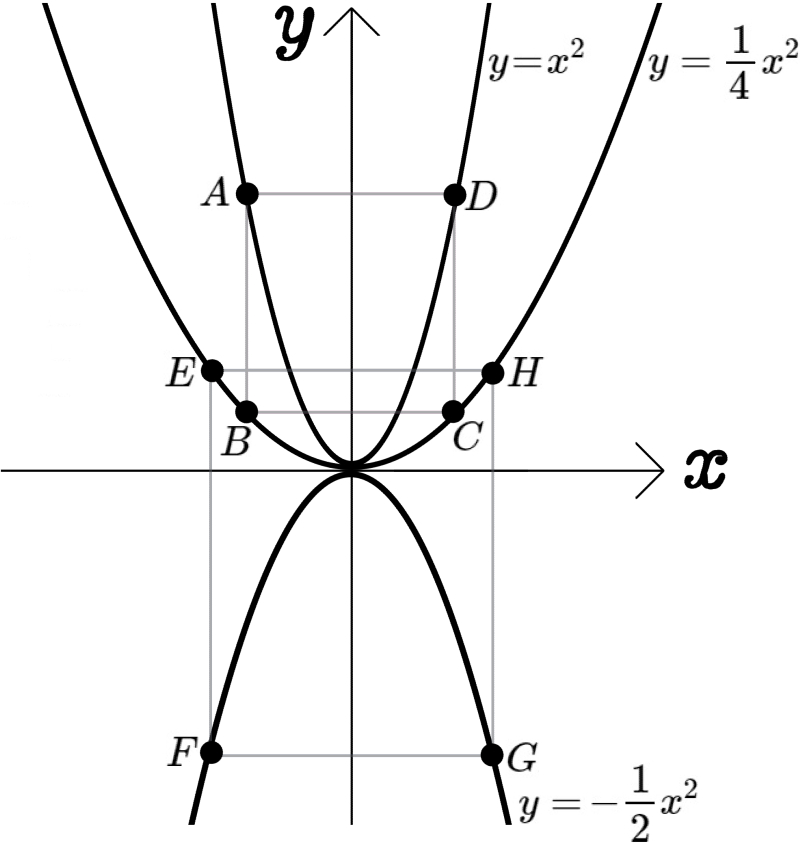 図のように、放物線 \(y=x^{2}\) 上に2点A、D、放物線\(y=\dfrac{1}{4}x^{2}\)上に4点B、C、E、H、放物線 \(y=-\dfrac{1}{2}x^{2}\) 上に2点F、Gがある。
図のように、放物線 \(y=x^{2}\) 上に2点A、D、放物線\(y=\dfrac{1}{4}x^{2}\)上に4点B、C、E、H、放物線 \(y=-\dfrac{1}{2}x^{2}\) 上に2点F、Gがある。
四角形ABCDと四角形EFGHの辺は座標軸に平行である。点Aと点Eの\(x\)座標は負であるものとして、次の問いに答えよ。
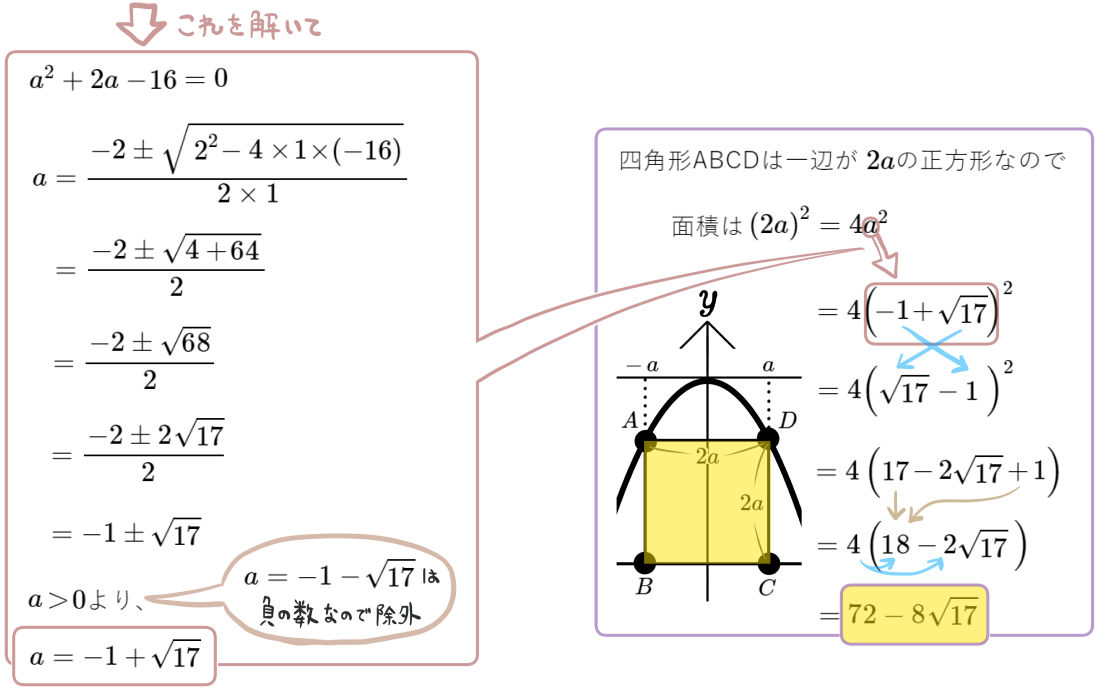
(1)点Aの\(x\)座標が \(-1\)のとき、四角形ABCDの面積を求めよ。

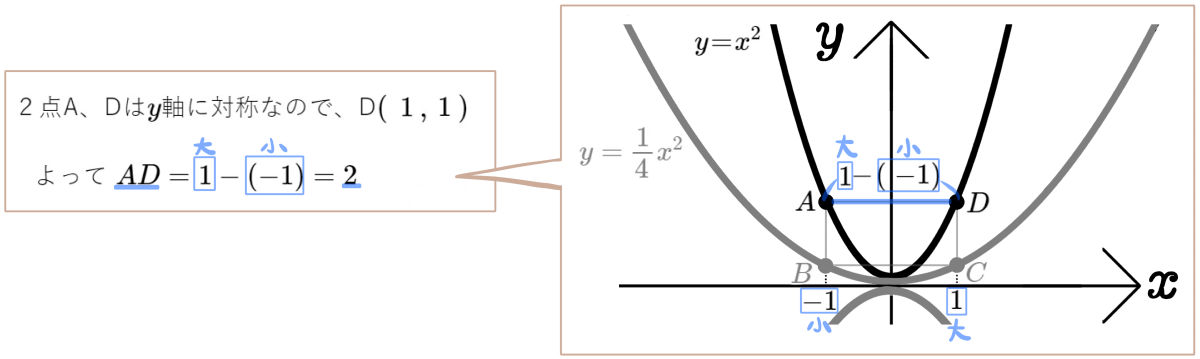

-\dfrac{8}{3} ,& \dfrac{64}{9}
\end{pmatrix}\)

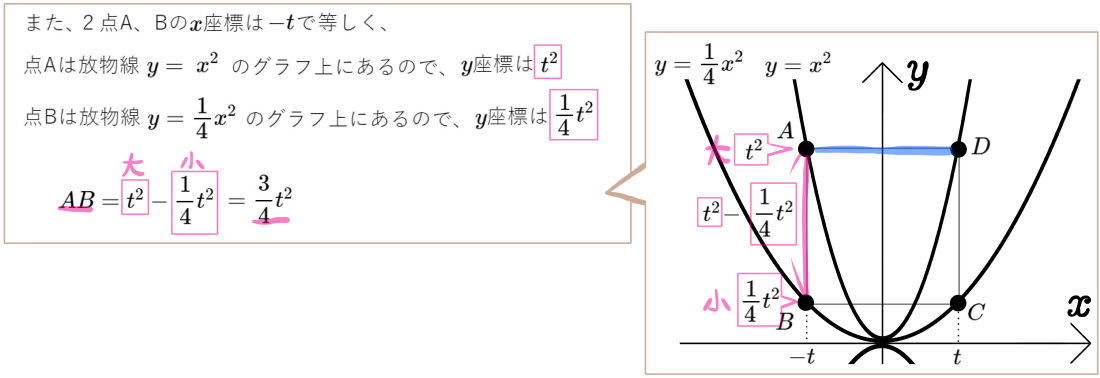


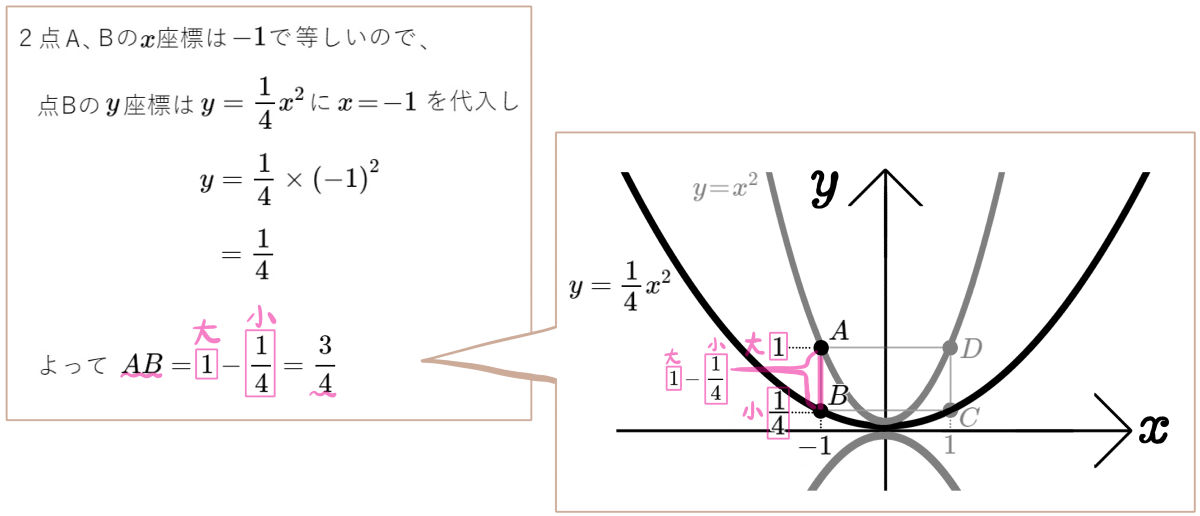
\dfrac{8}{3} ,& \dfrac{16}{9}
\end{pmatrix}\)


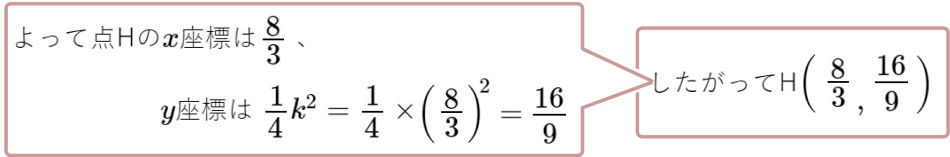
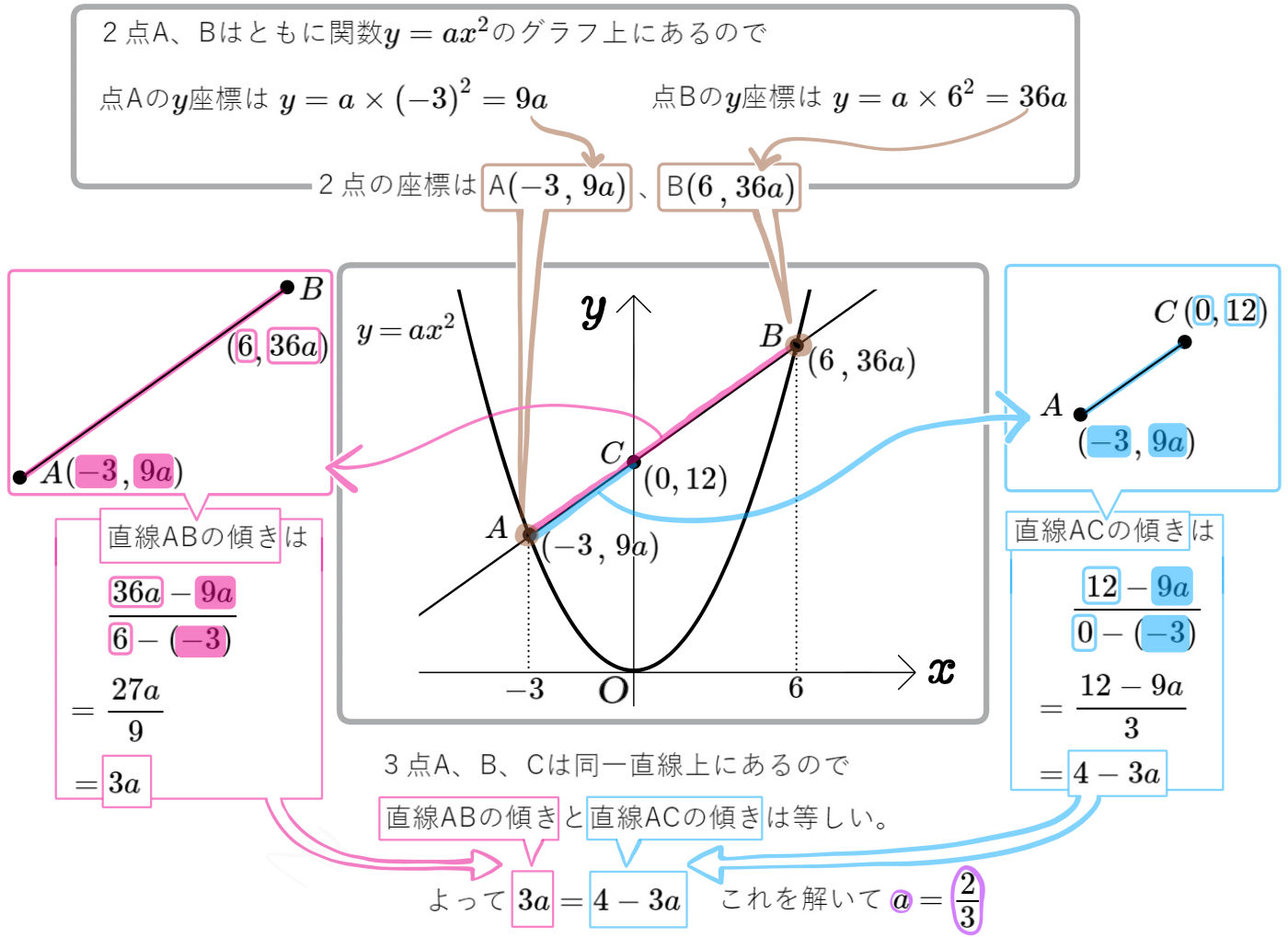
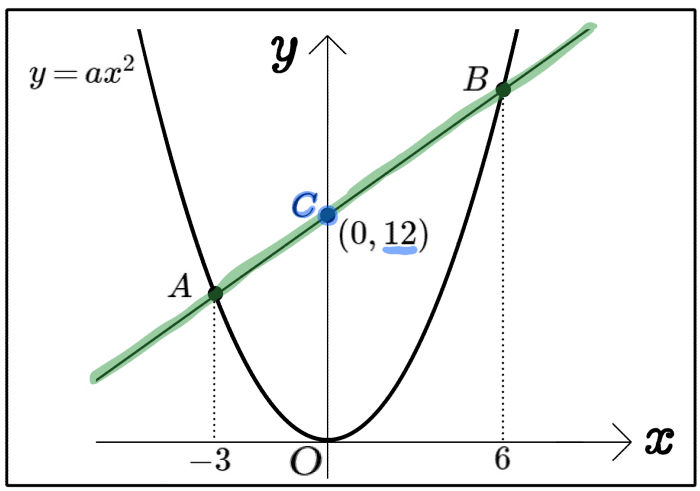
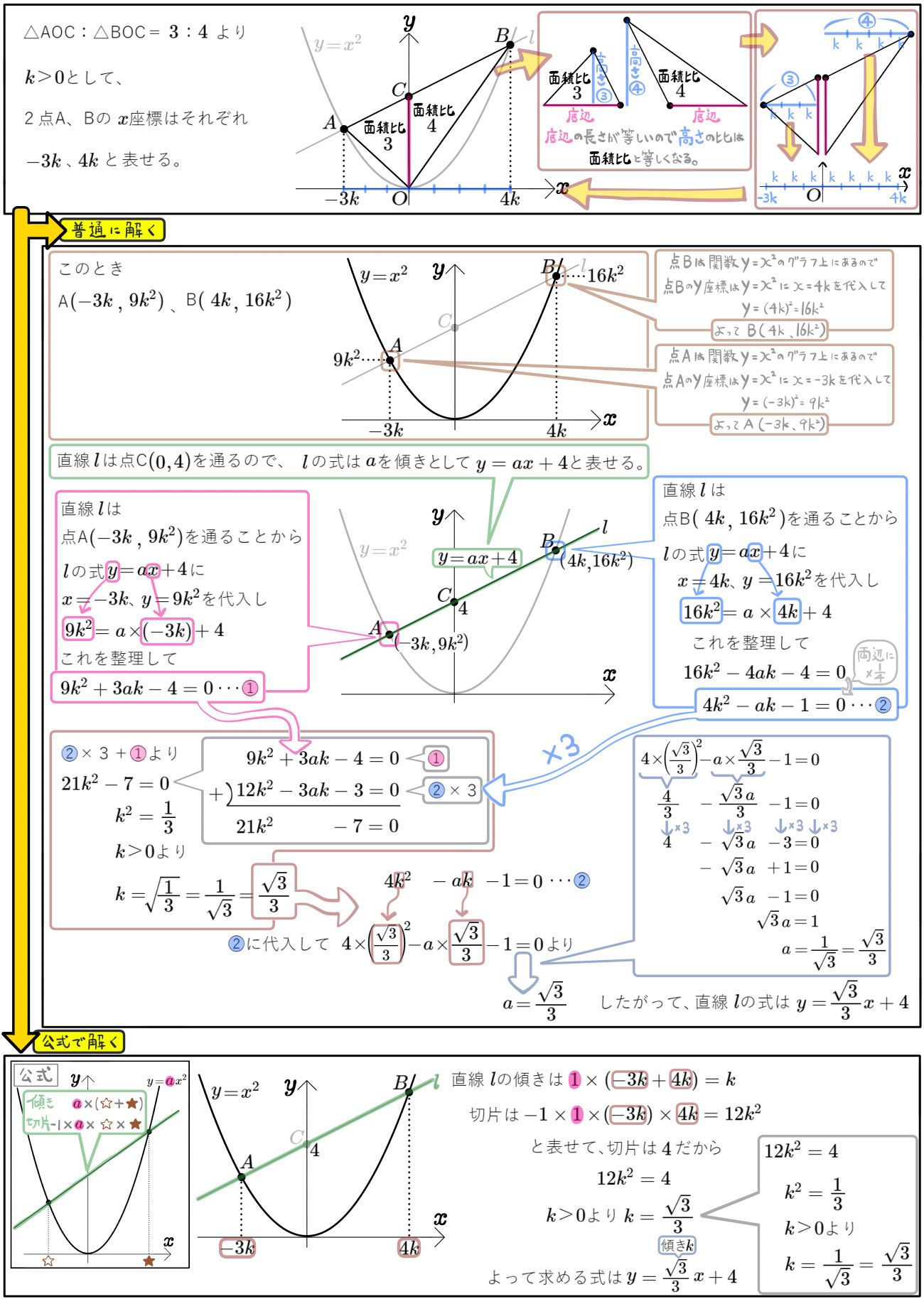
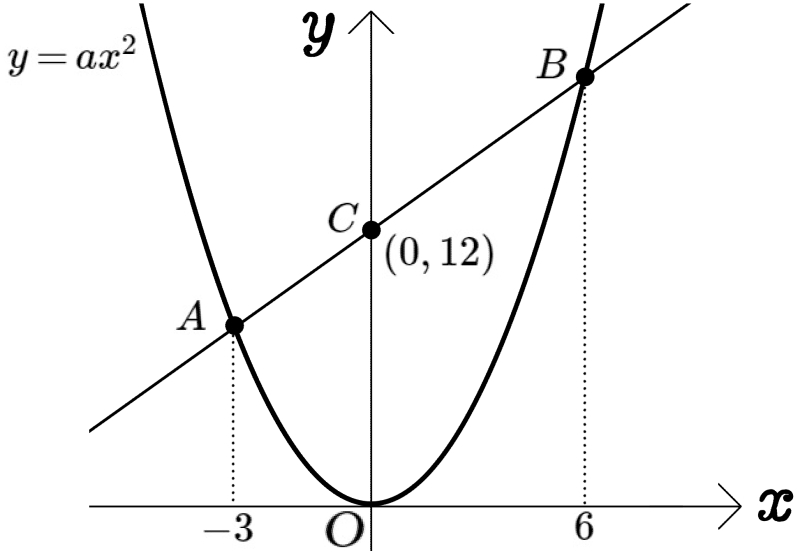 図にある曲線は、関数\(y=ax^{2}\)のグラフで、そのグラフ上にある2点A、Bの\(x\)座標は、それぞれ \(-3\)、 \(6\)である。
図にある曲線は、関数\(y=ax^{2}\)のグラフで、そのグラフ上にある2点A、Bの\(x\)座標は、それぞれ \(-3\)、 \(6\)である。
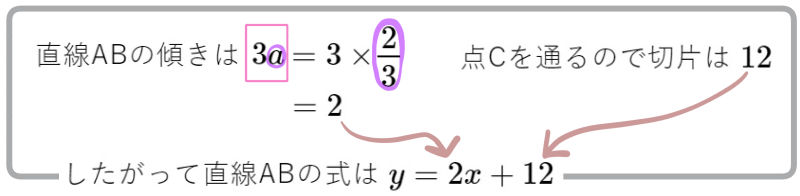
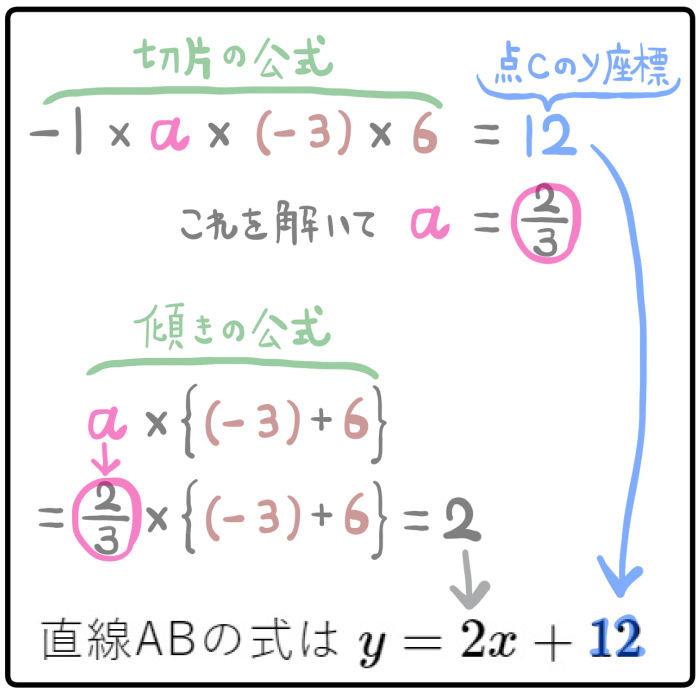
また、直線ABが \(y\)軸と点C( 0 , 12 )で交わるとき、 定数\(a\) の値と直線ABの式を求めよ。
2次関数の難問・応用問題|中学数学~高校入試


ただしその中には、一般的な難易度の定期テストには基本的には出題されない問題も含まれています。
もちろん学校のテスト難易度や、先生の出題傾向によっては出題の可能性はあります。
ただ、定期テスト対策として利用される場合は、基本的にはひとまず除外して学習を進めることをおすすめします。
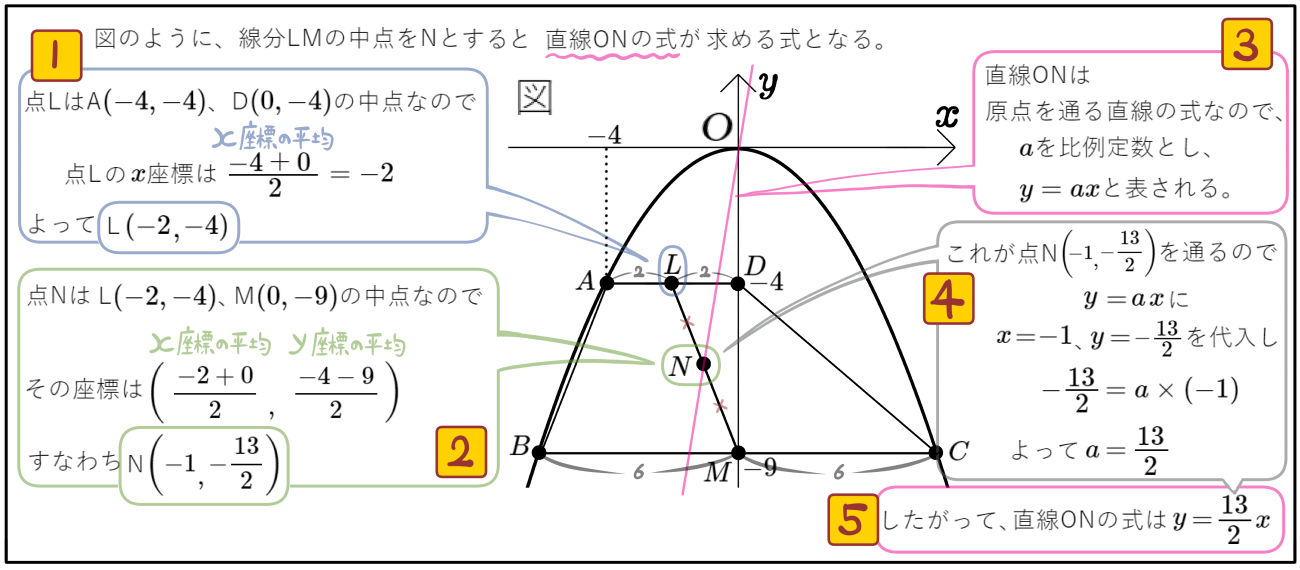
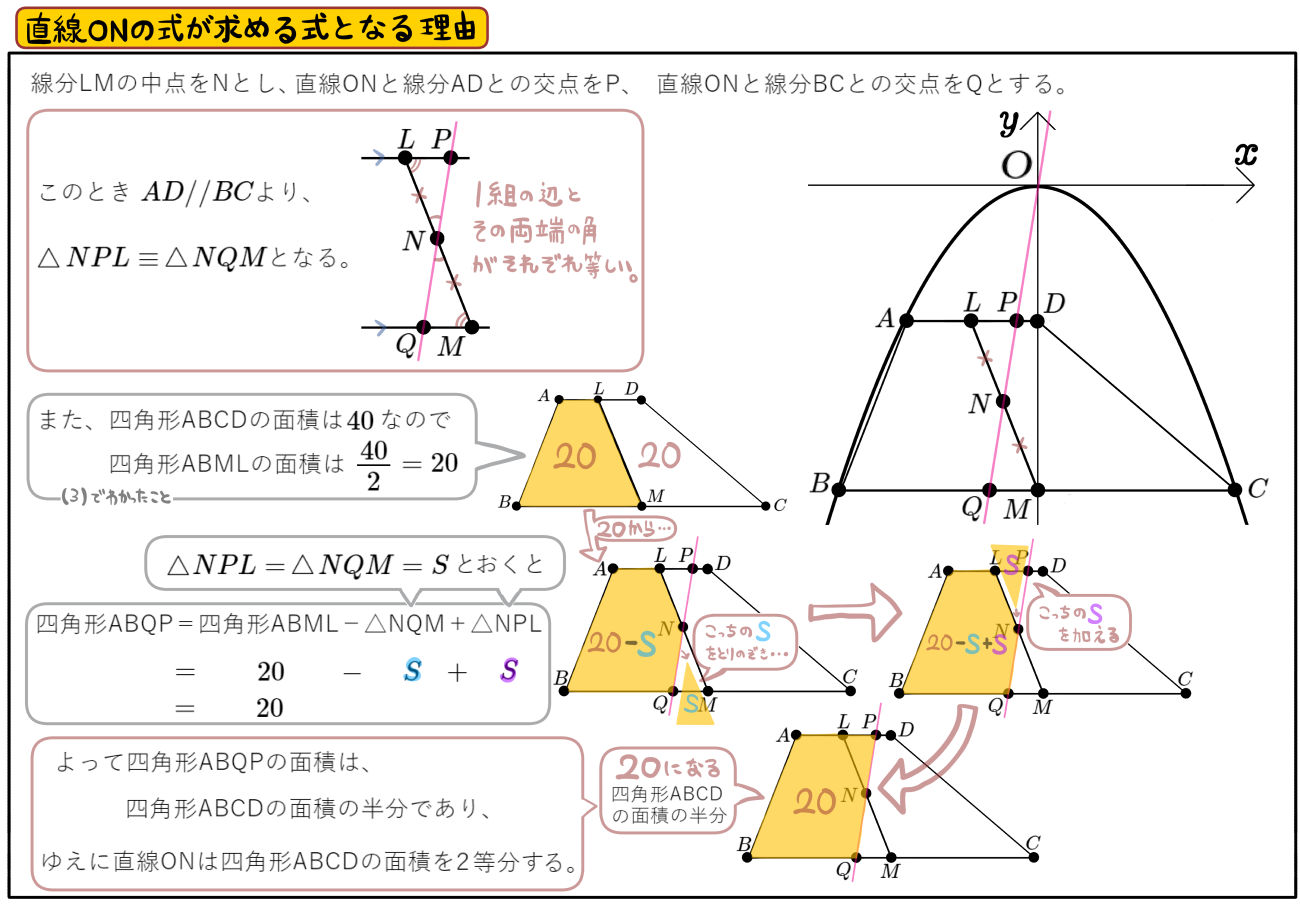
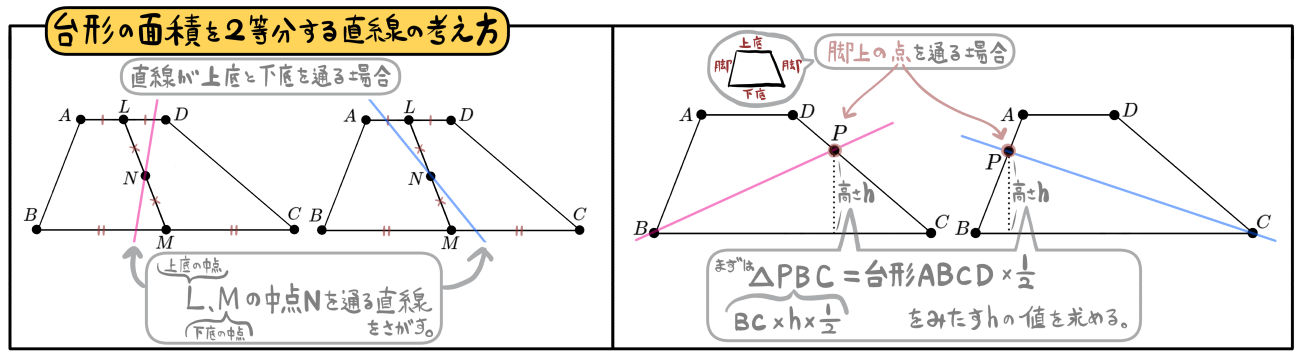
【15】の(4)では、この左側にまとめてある「2点L、Mの中点Nを通る直線」についてあつかっています。これについてはまず出題されません。
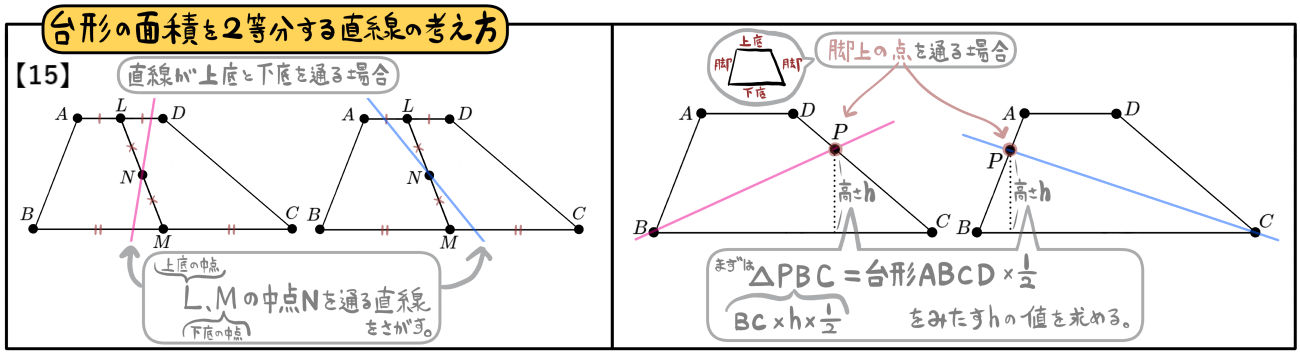
【8】の(3)と【11】にて使用しています。
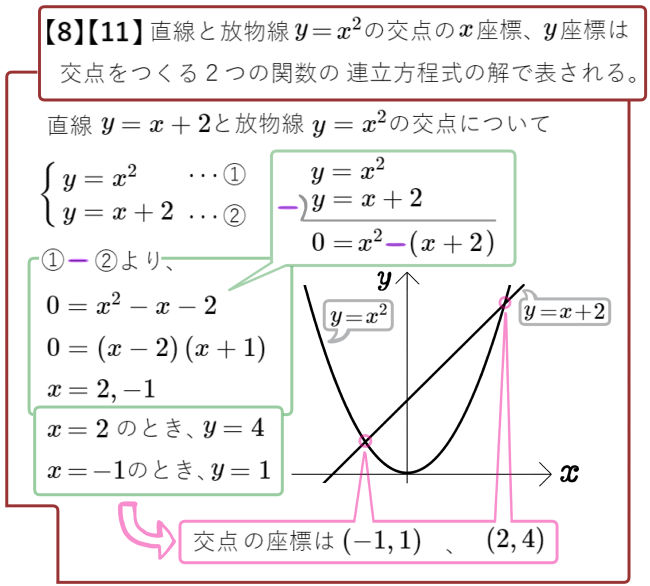
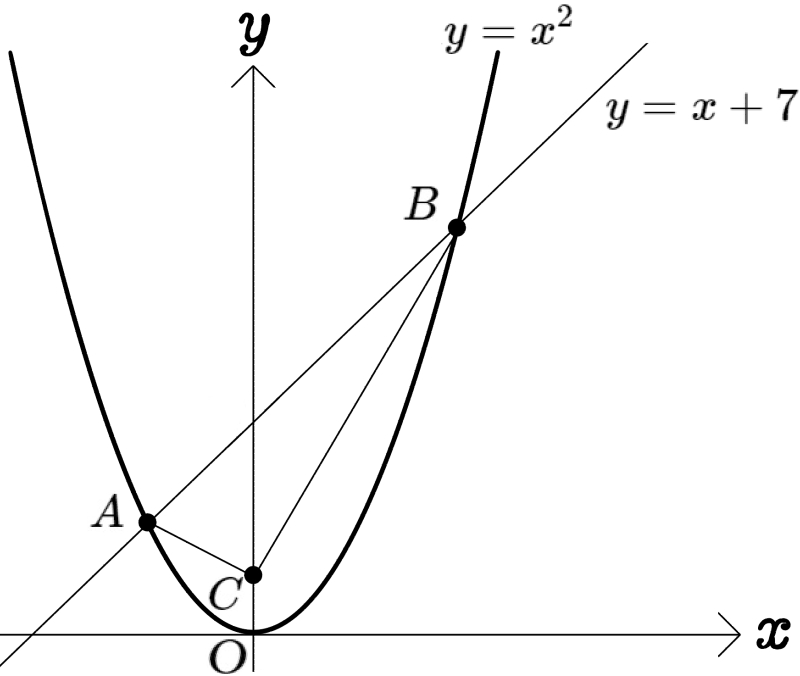 図のように、放物線\(y=x^{2}\)と直線 \(y=x+7\)の交点をA、Bとする。点Cの座標を( 0 , 2 )とする。このとき、△ABC=△ABPとなる点Pについて考える。次の問いに答えよ。
図のように、放物線\(y=x^{2}\)と直線 \(y=x+7\)の交点をA、Bとする。点Cの座標を( 0 , 2 )とする。このとき、△ABC=△ABPとなる点Pについて考える。次の問いに答えよ。
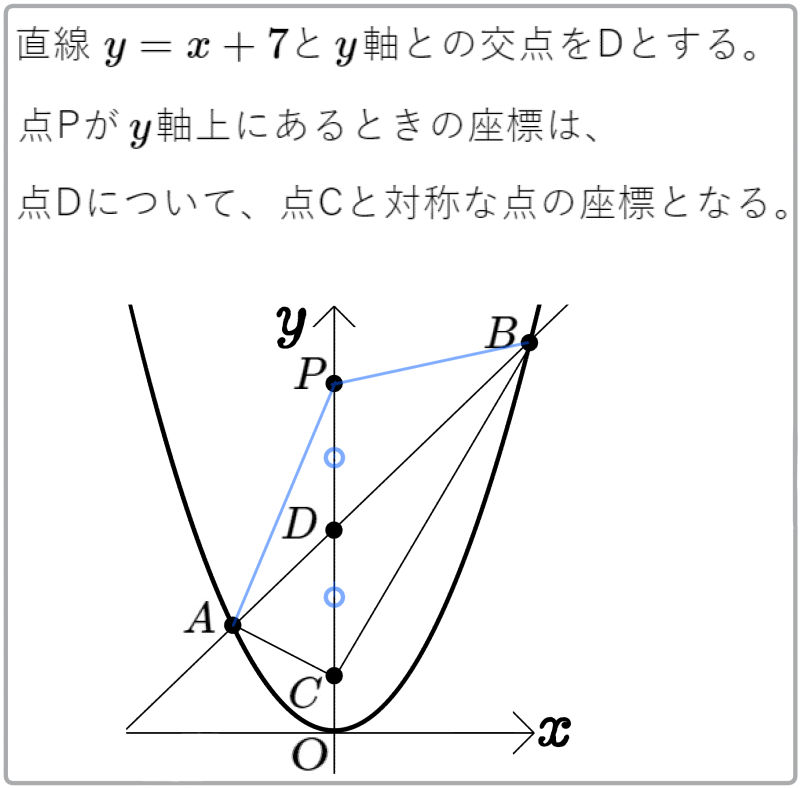
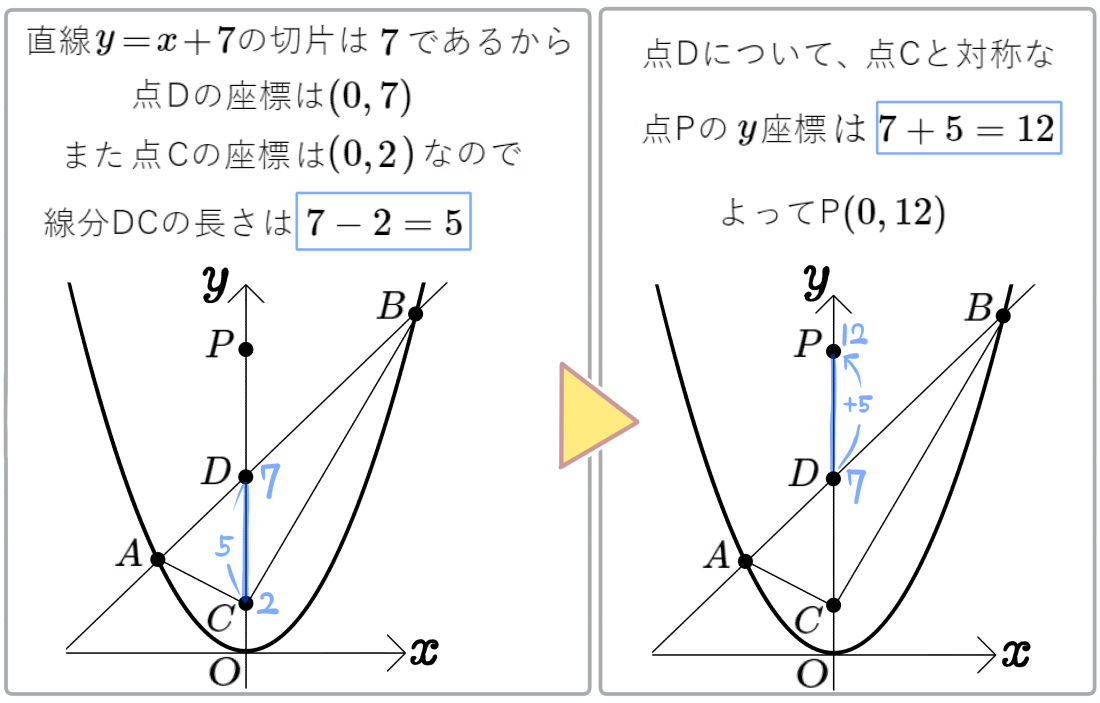
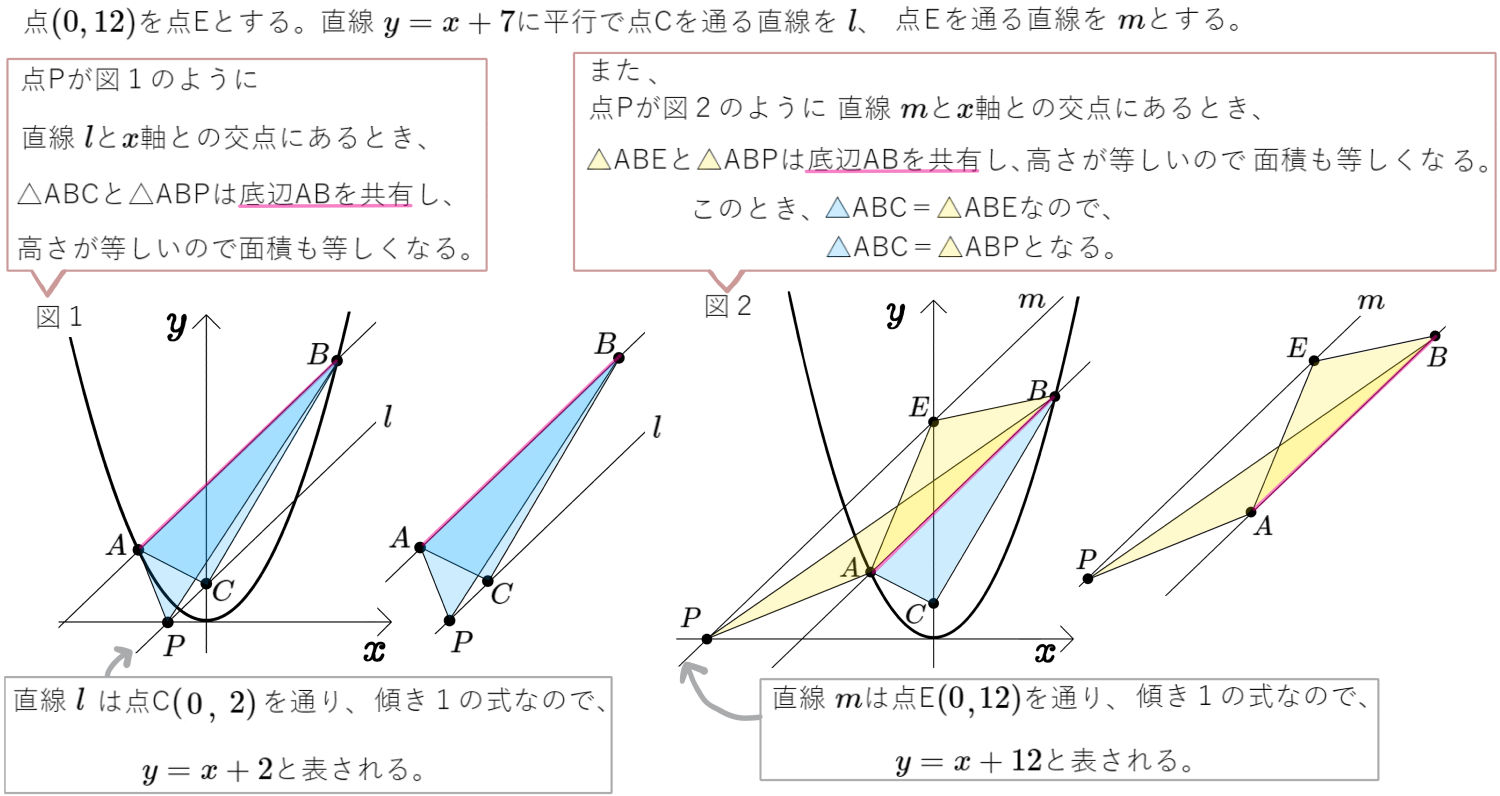
(1)点Pが点Cとは異なる\(y\)軸上にあるとき、点Pの座標を求めよ。

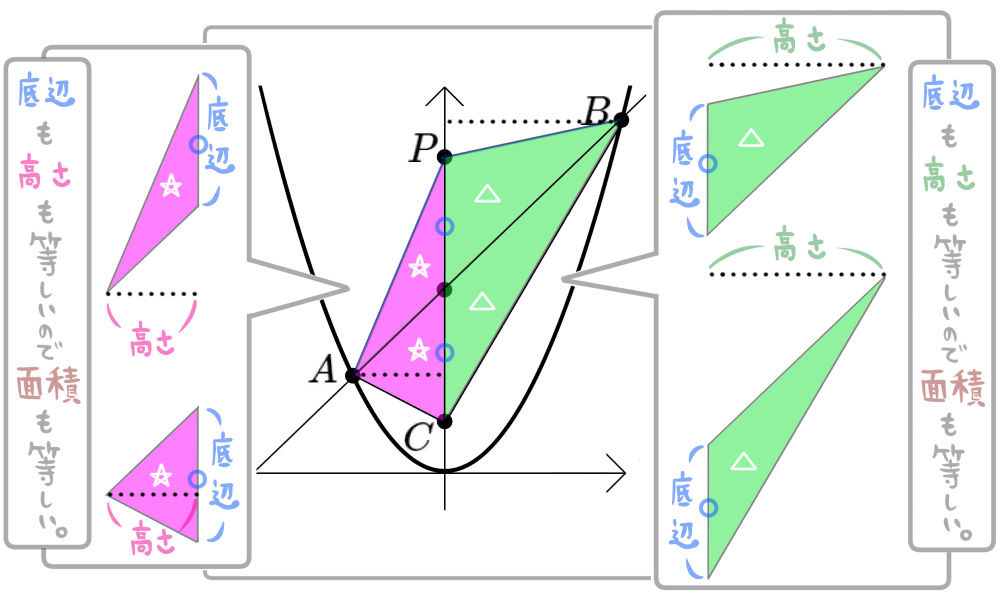

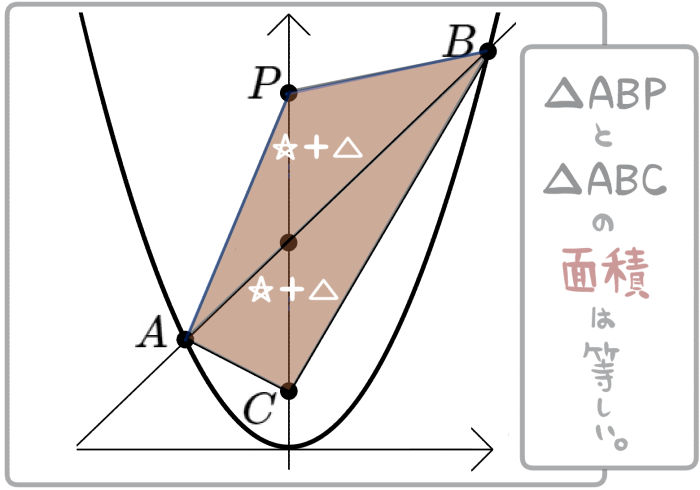

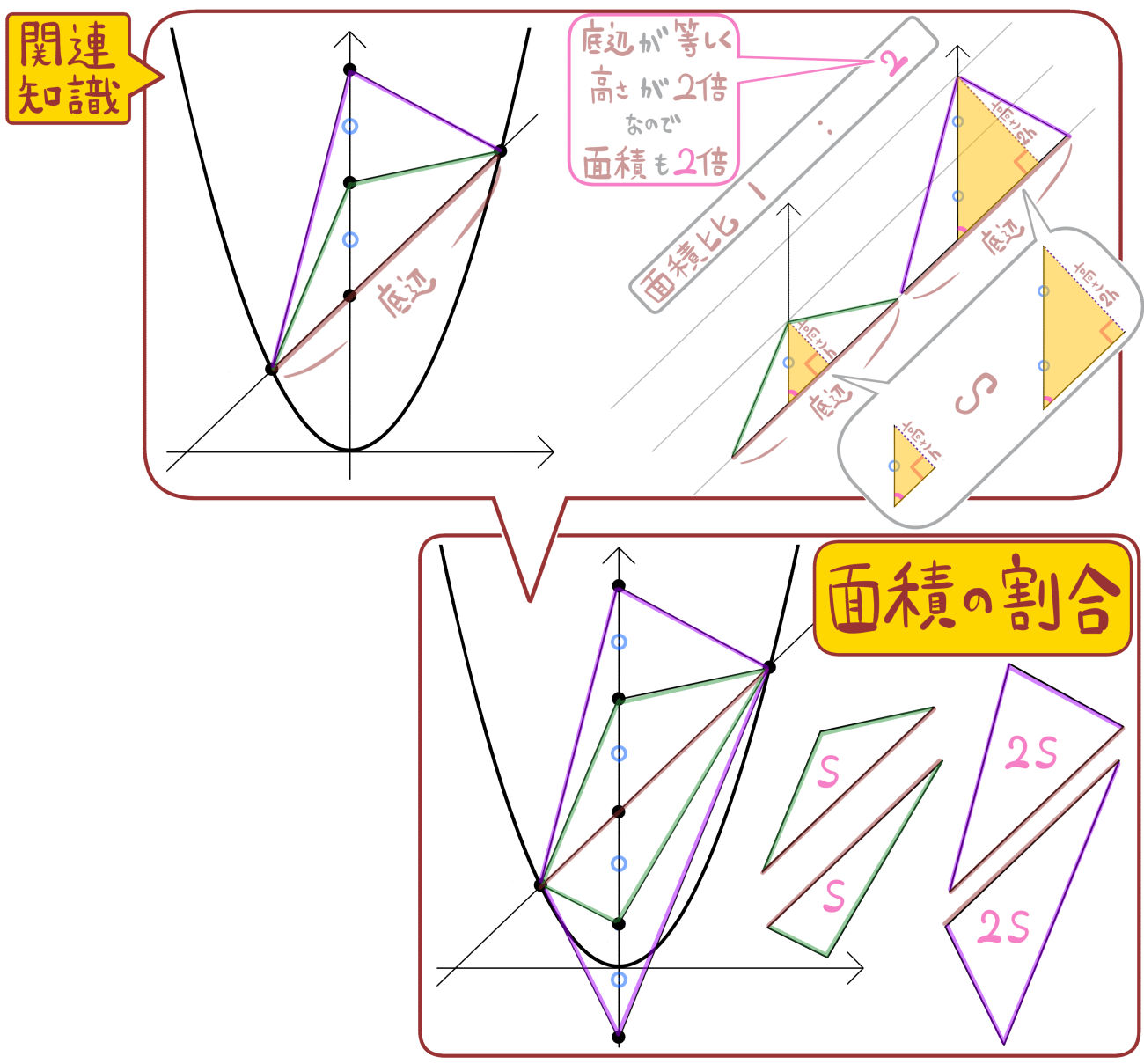
ちなみにこのテーマの問題でよく使う知識も紹介しておきます。


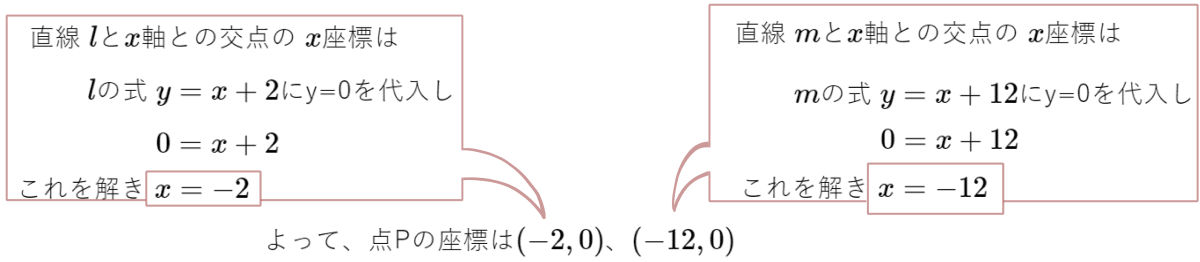
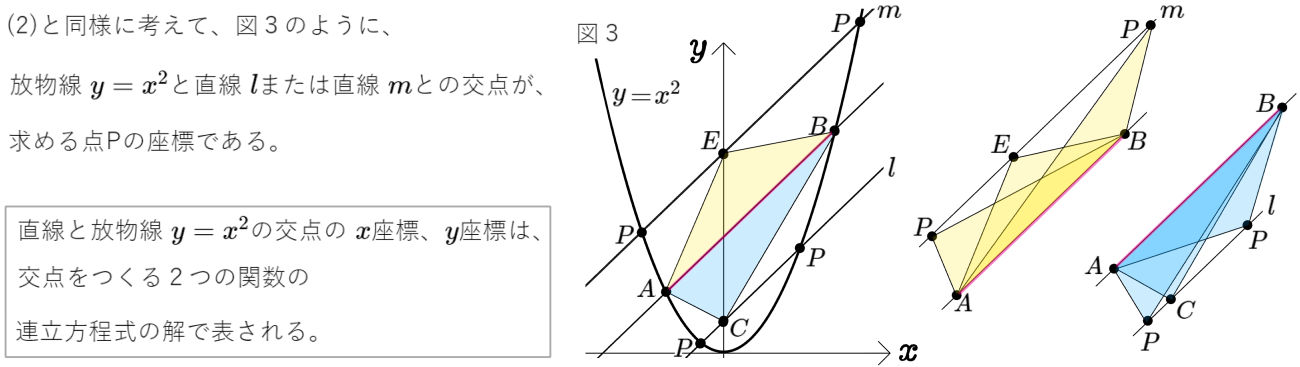
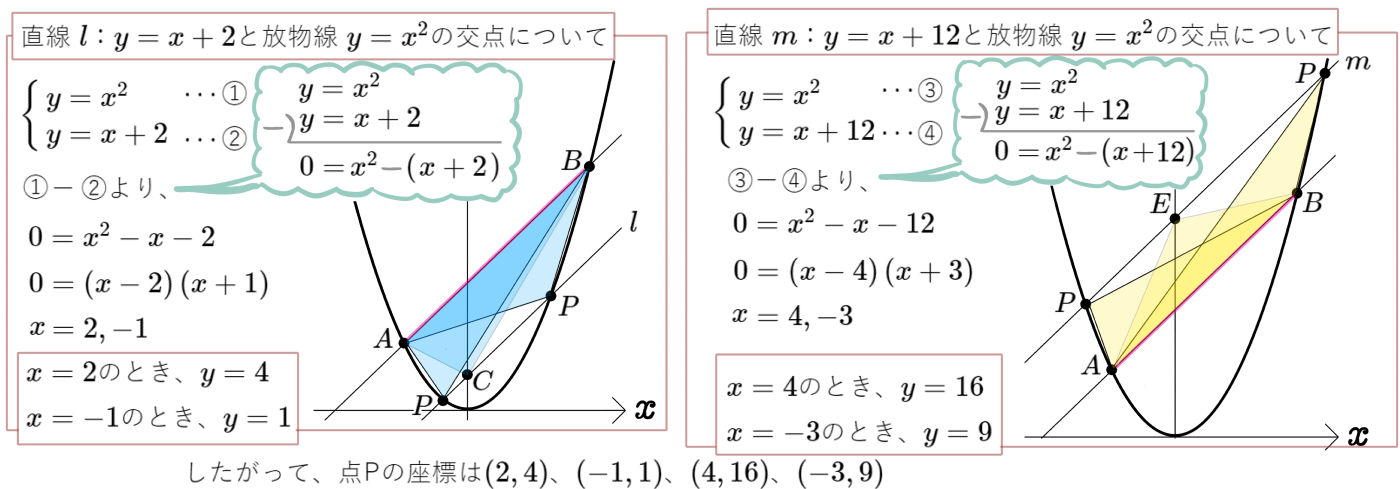
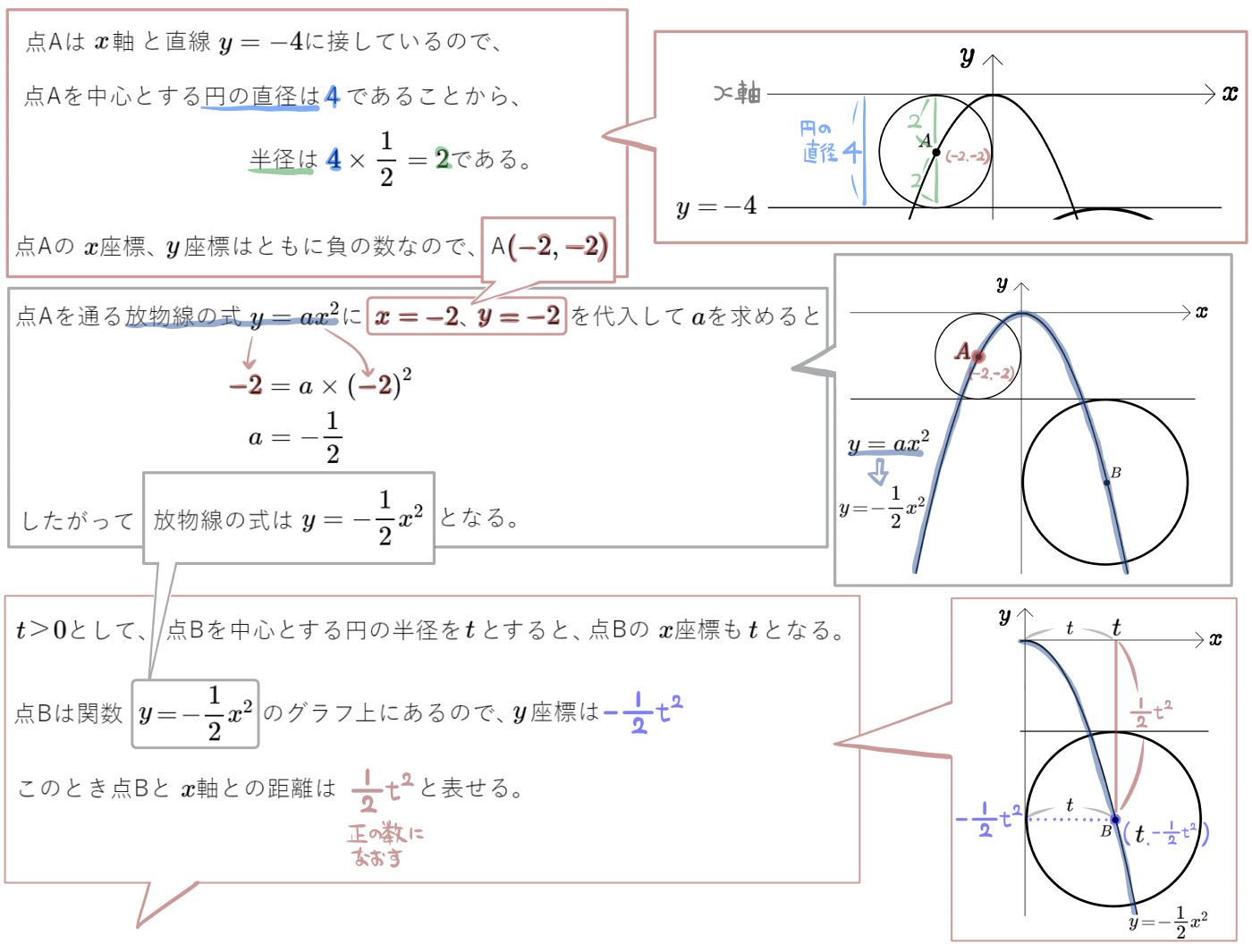
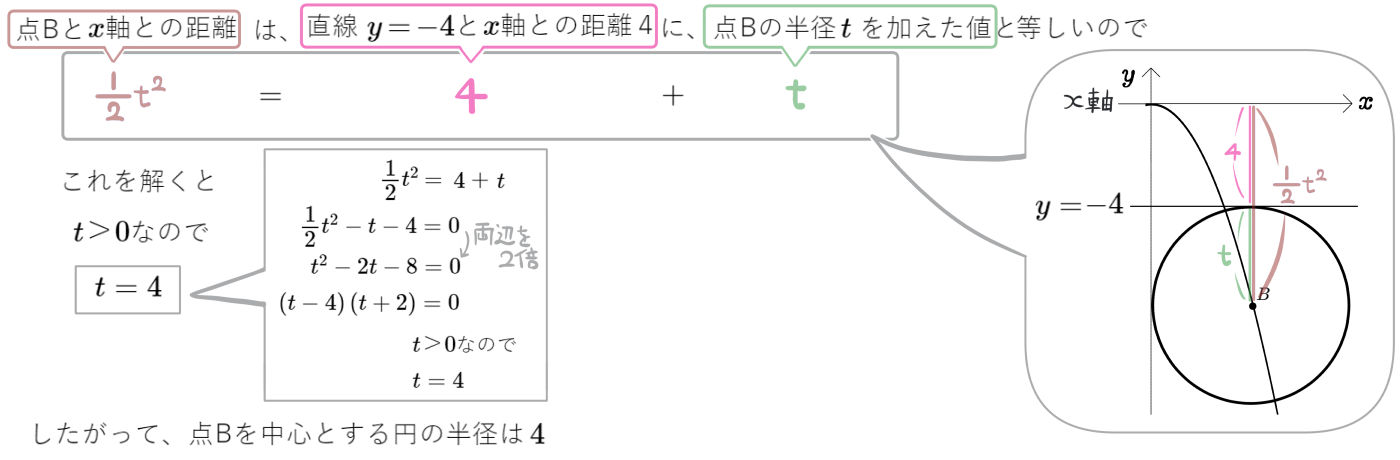
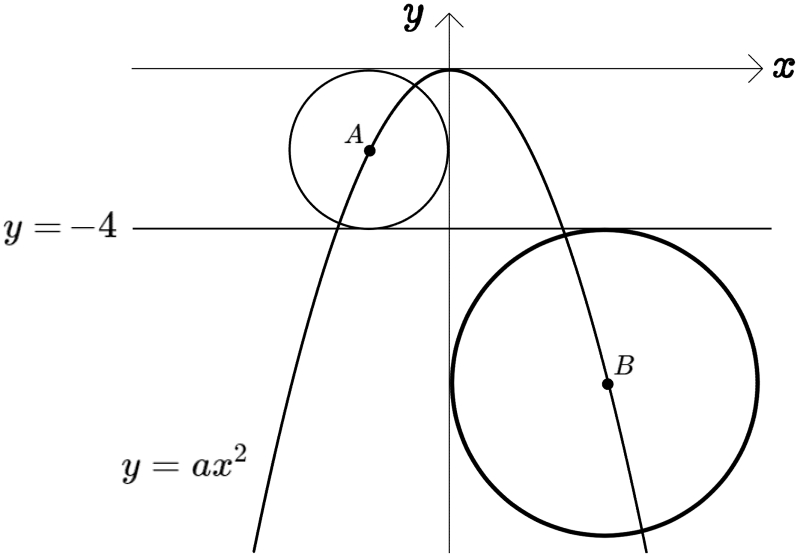 図のように、放物線 \(y=ax^{2}\) のグラフ上に2点A、Bをそれぞれ中心とする2つの円があり、2つの円はともに\(y\)軸と直線 \(y=-4\) に接している。このとき点Bを中心とする円の半径を求めよ。
図のように、放物線 \(y=ax^{2}\) のグラフ上に2点A、Bをそれぞれ中心とする2つの円があり、2つの円はともに\(y\)軸と直線 \(y=-4\) に接している。このとき点Bを中心とする円の半径を求めよ。
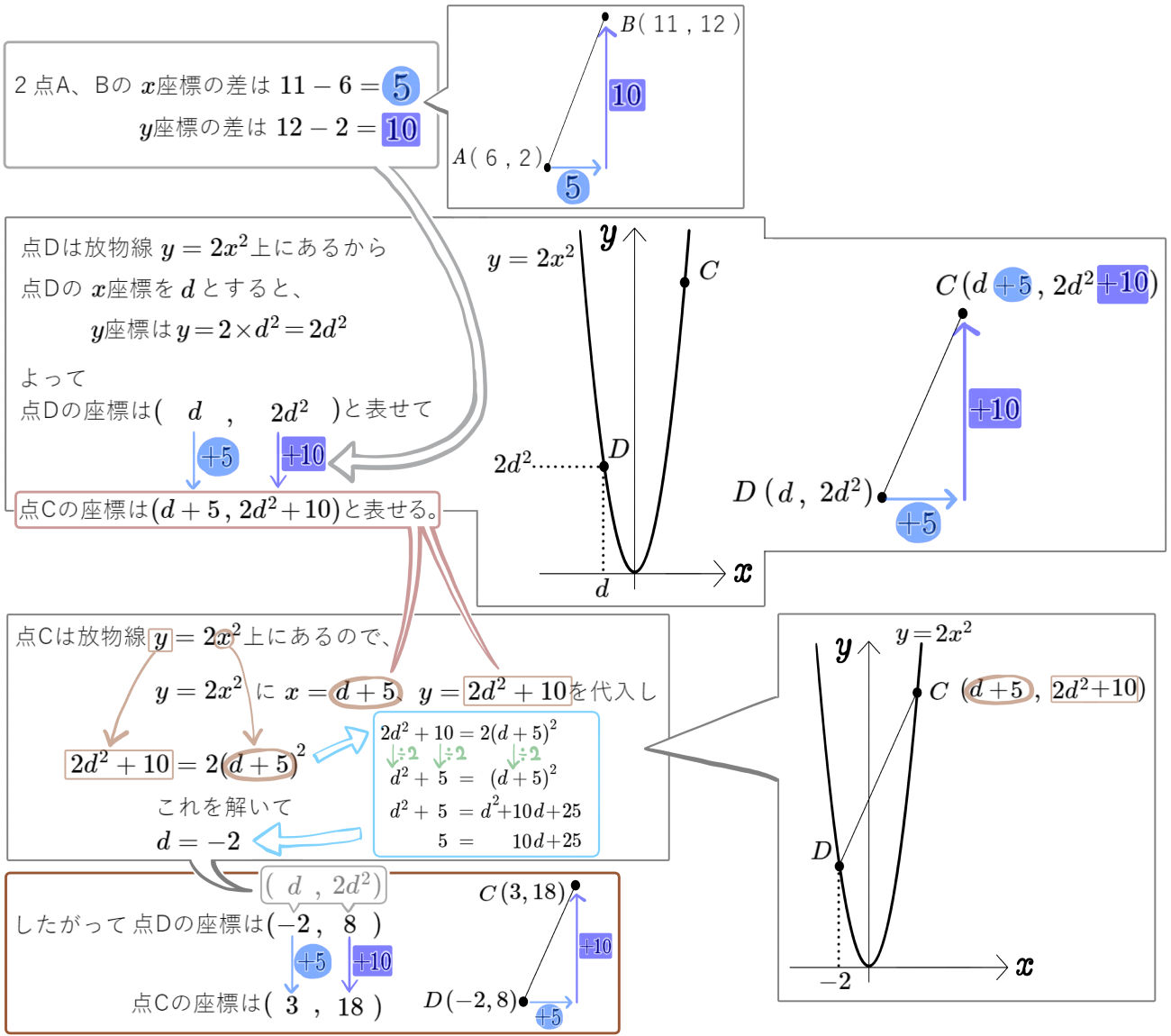
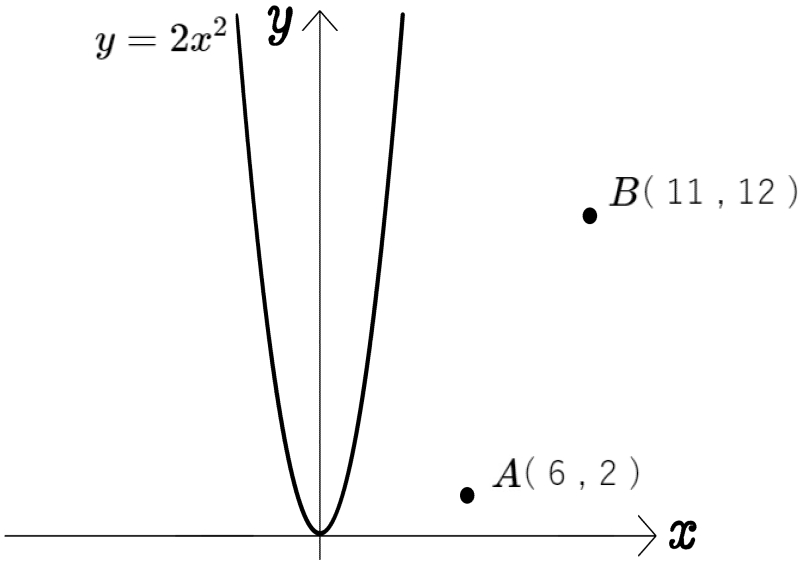 図のように、放物線 \(y=2x^{2}\)と2点A( 6 , 2 )、B( 11 , 12 )がある。
図のように、放物線 \(y=2x^{2}\)と2点A( 6 , 2 )、B( 11 , 12 )がある。
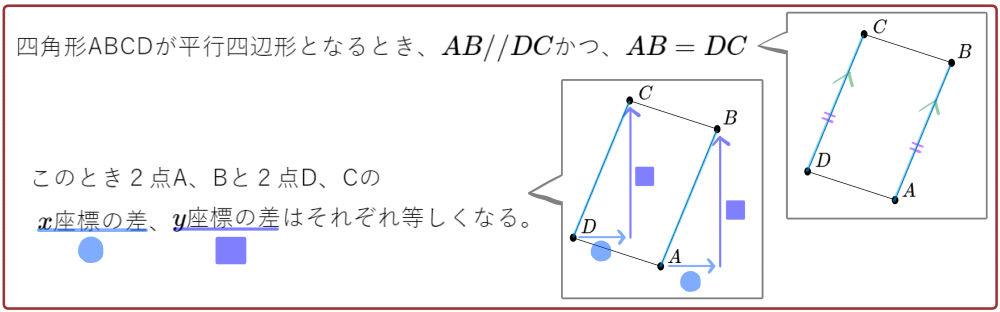
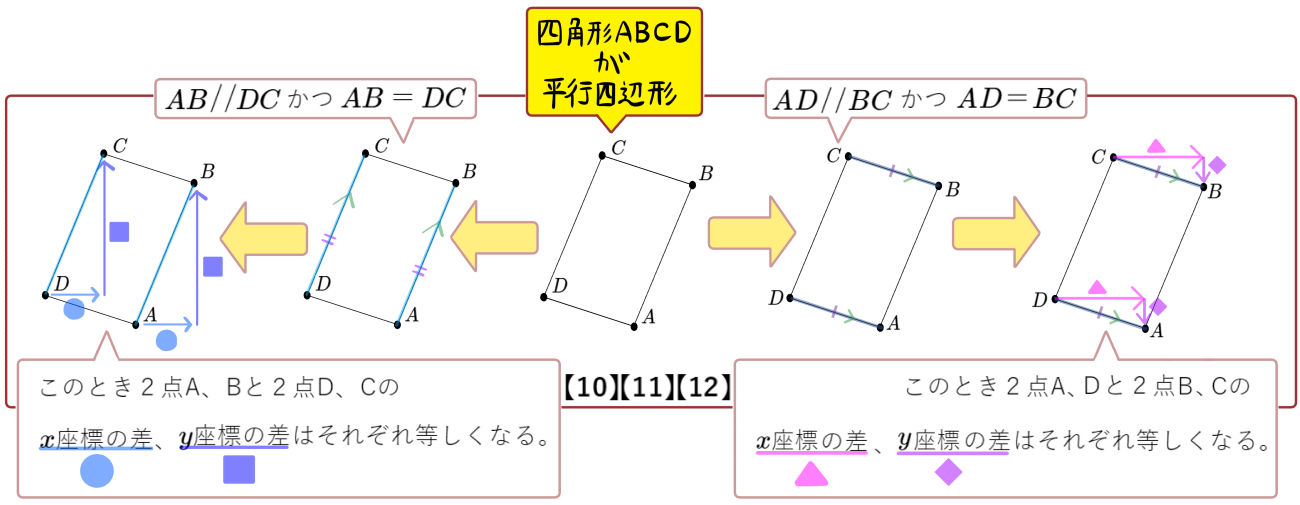
四角形ABCDが平行四辺形となるように、放物線 \(y=2x^{2}\)に2点C、Dをとるとき、2点C、Dの座標をそれぞれ求めよ。

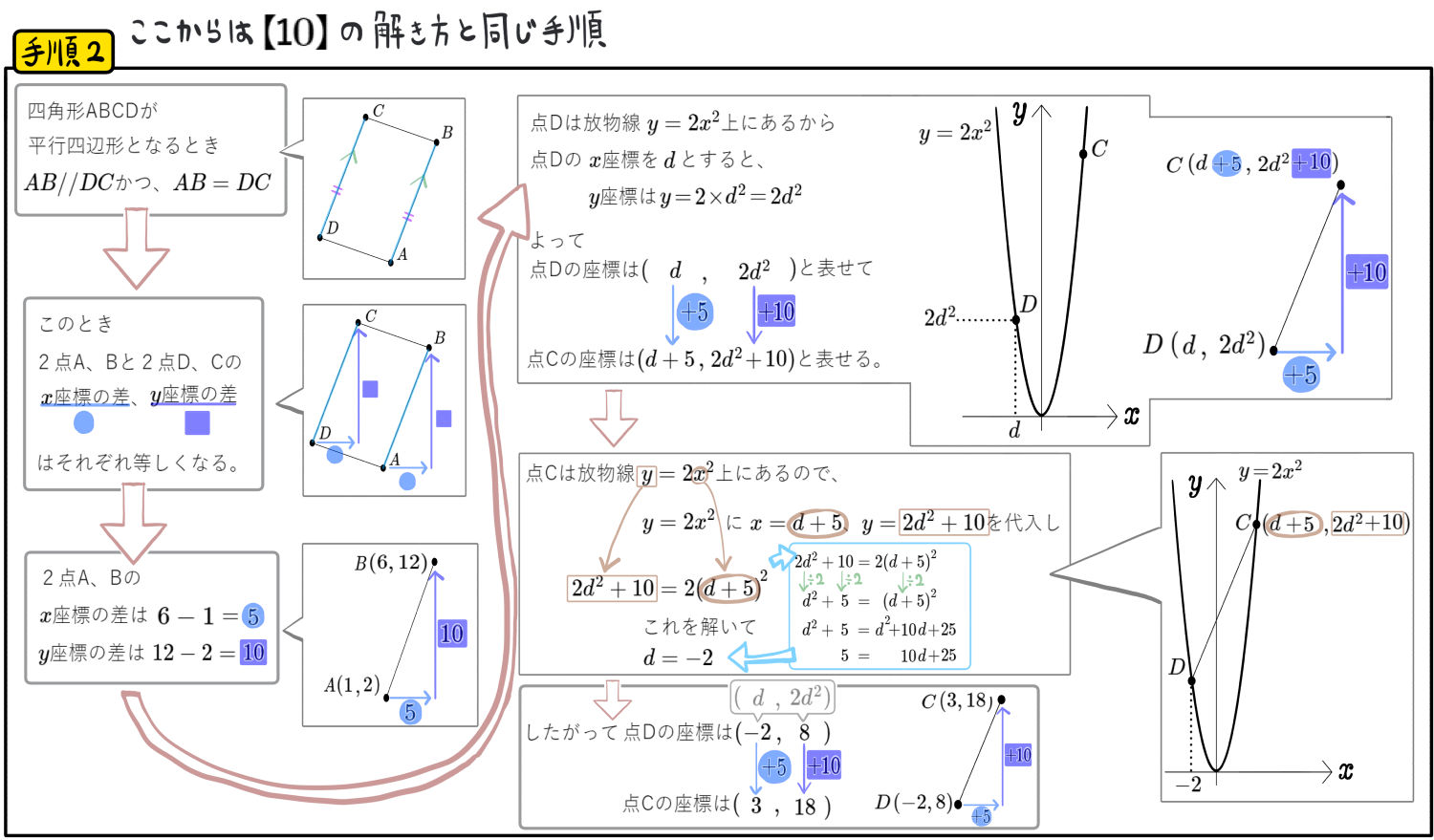
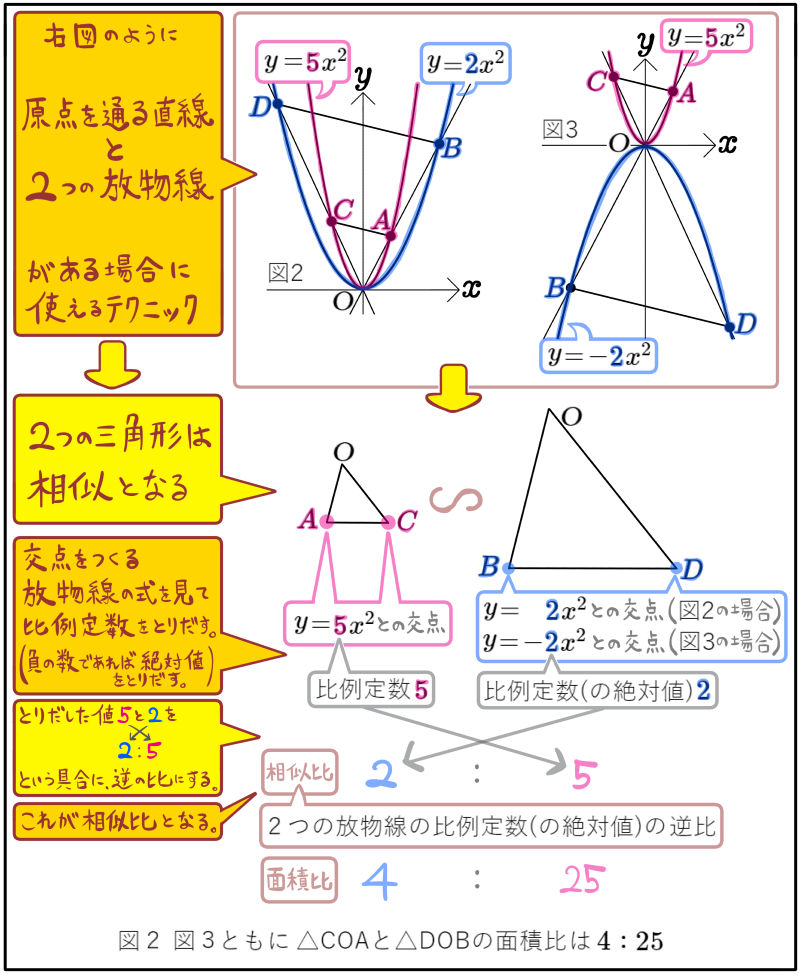
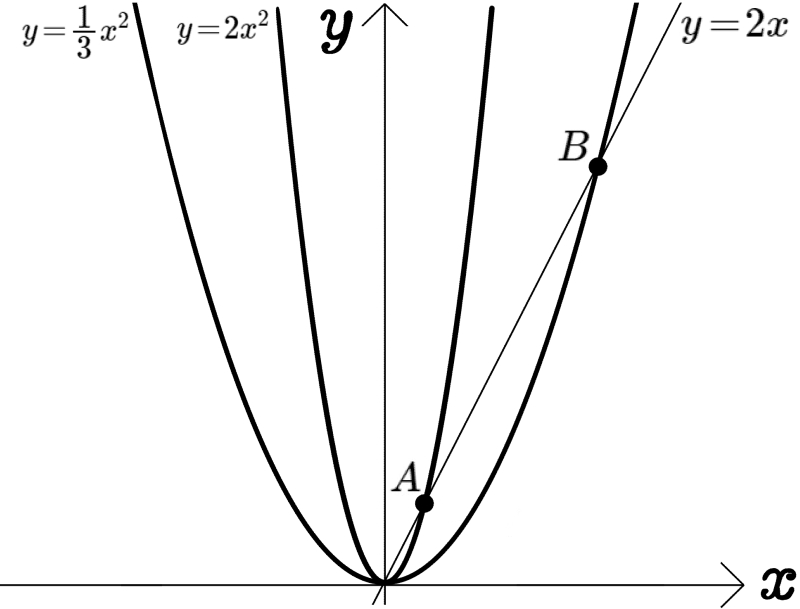 図のように、直線\(y=2x\)に対し、放物線\(y=2x^{2}\)、 放物線\(y=\dfrac{1}{3}x^{2}\) との原点を除く交点をそれぞれA、Bとする。四角形ABCDが平行四辺形となるように、放物線\(y=2x^{2}\)上に2点C、Dをとるとき、2点の座標をそれぞれ求めよ。
図のように、直線\(y=2x\)に対し、放物線\(y=2x^{2}\)、 放物線\(y=\dfrac{1}{3}x^{2}\) との原点を除く交点をそれぞれA、Bとする。四角形ABCDが平行四辺形となるように、放物線\(y=2x^{2}\)上に2点C、Dをとるとき、2点の座標をそれぞれ求めよ。





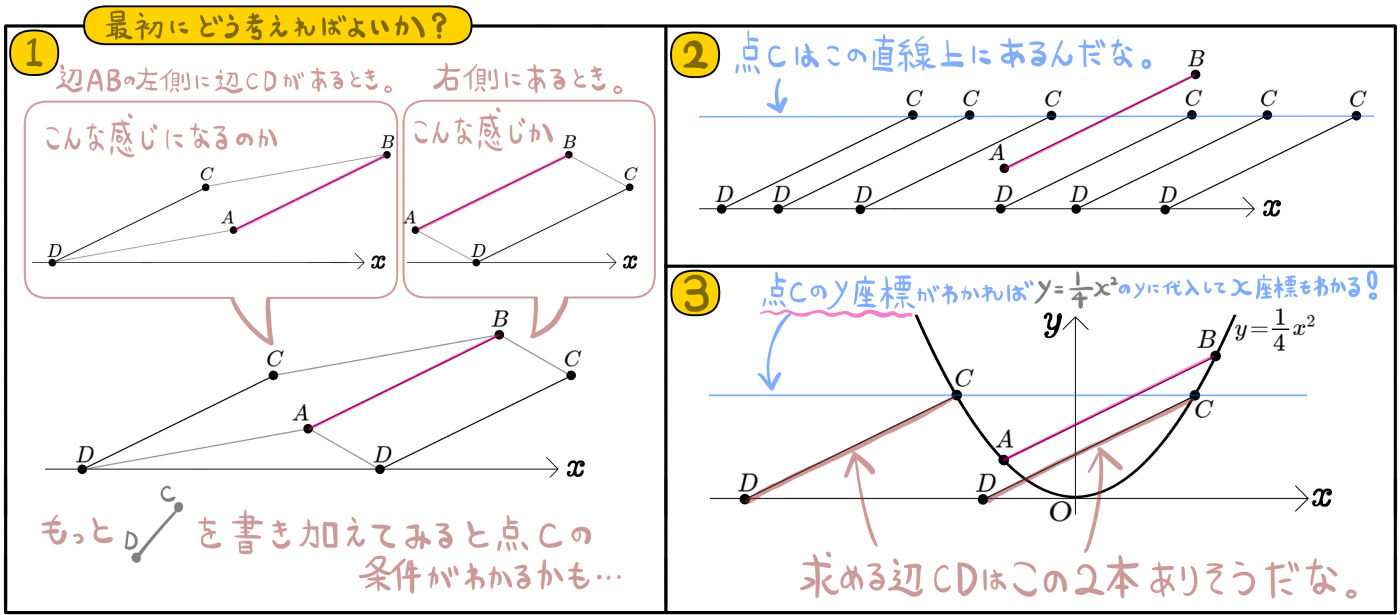
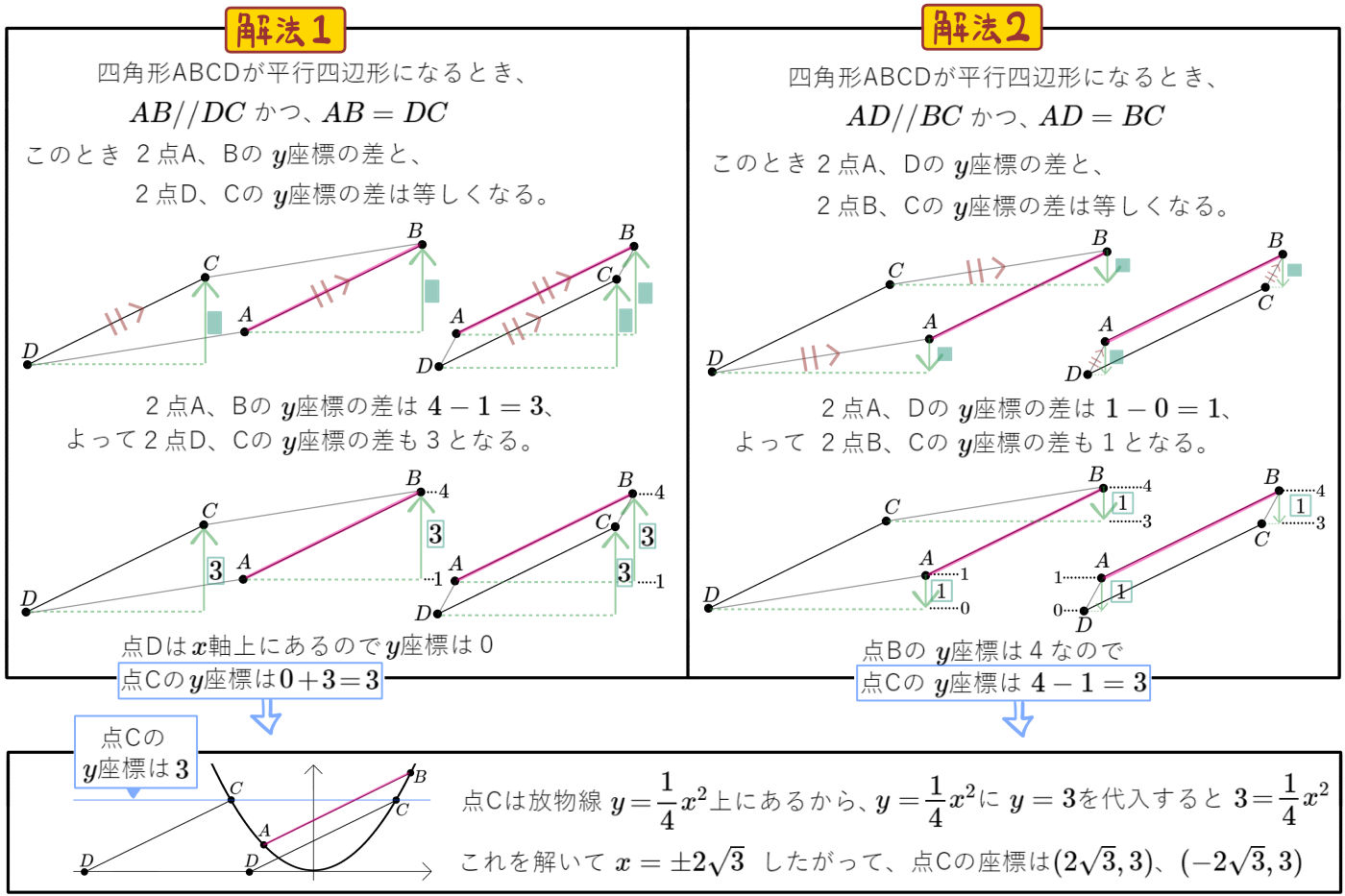
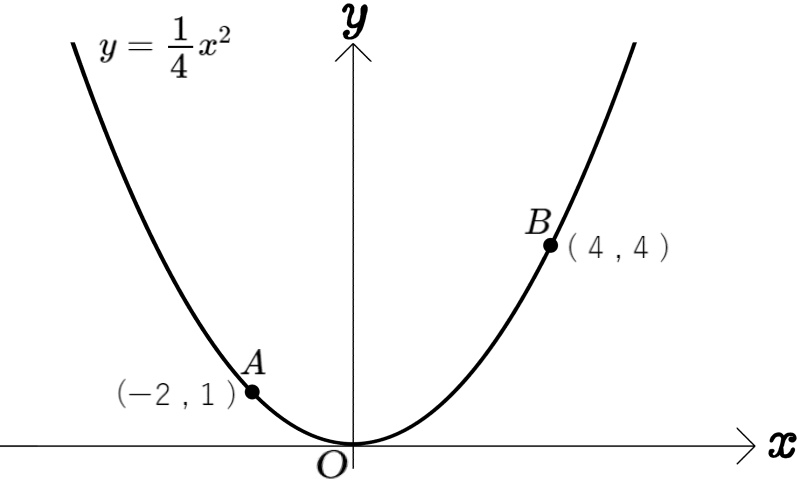 図のように、放物線\(y=\dfrac{1}{4}x^{2}\)のグラフ上に2点A、Bがあり、2点の座標は、\(A( -2 , 1 )\)、\(B( 4 , 4 )\)である。放物線\(y=\dfrac{1}{4}x^{2}\)上に3点A、B、Oと異なる点Cをとり、点Cを通り直線ABに平行な直線と\(x\)軸との交点をDとする。
図のように、放物線\(y=\dfrac{1}{4}x^{2}\)のグラフ上に2点A、Bがあり、2点の座標は、\(A( -2 , 1 )\)、\(B( 4 , 4 )\)である。放物線\(y=\dfrac{1}{4}x^{2}\)上に3点A、B、Oと異なる点Cをとり、点Cを通り直線ABに平行な直線と\(x\)軸との交点をDとする。
このとき四角形ABCDが平行四辺形となるような点Cの座標をすべて求めよ。




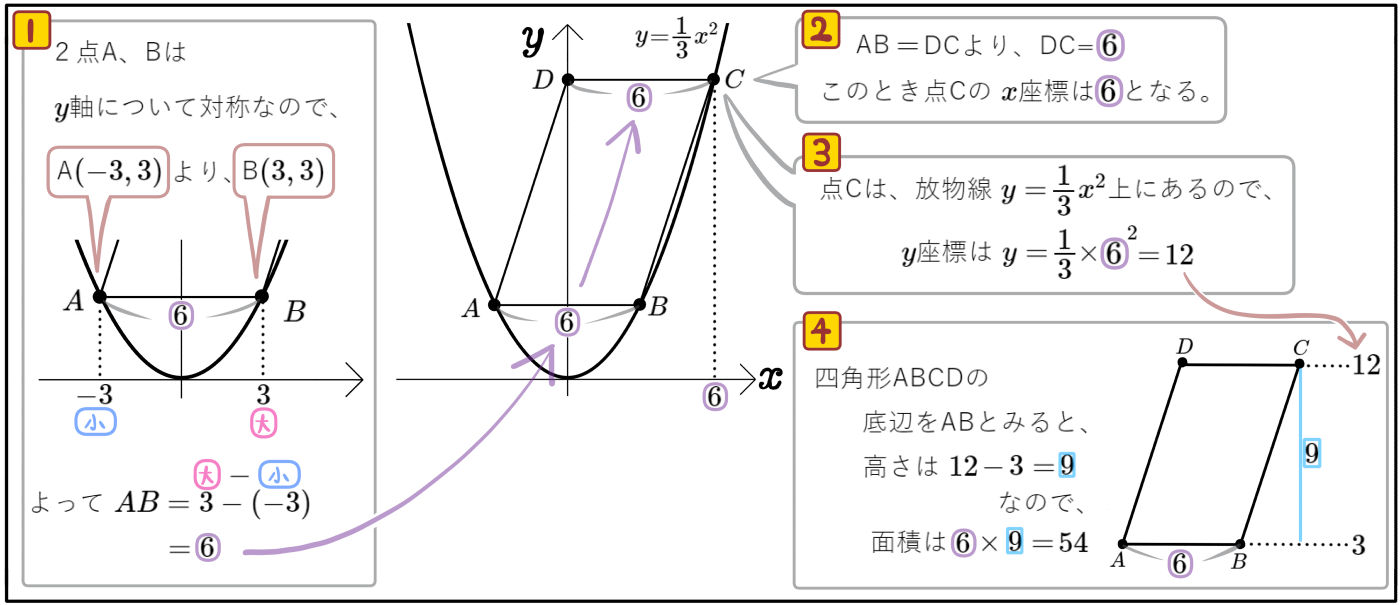
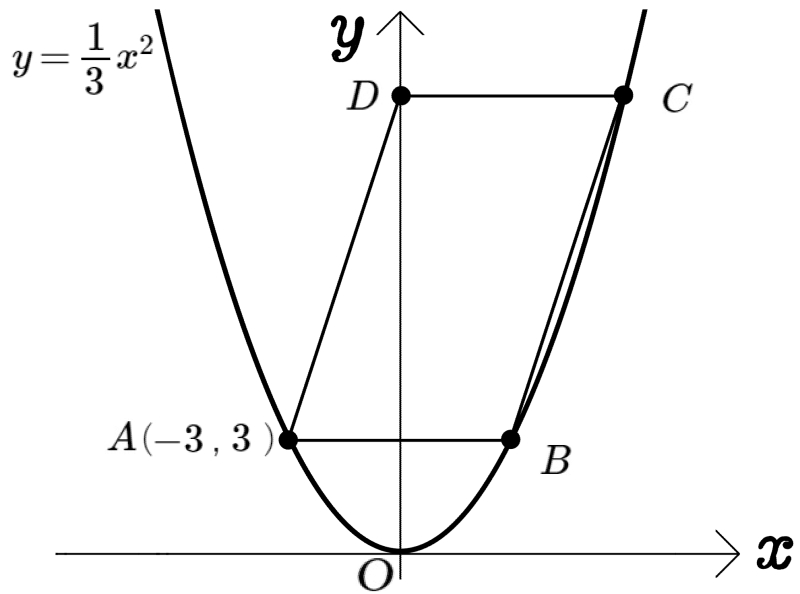 図のように、放物線\(y=\dfrac{1}{3}x^{2}\)上に3点A、B、Cがあり、\(y\)軸上に点Dがある。
図のように、放物線\(y=\dfrac{1}{3}x^{2}\)上に3点A、B、Cがあり、\(y\)軸上に点Dがある。
点Aの座標が\(( -3 , 3 )\)、線分ABは \(x\)軸と平行であり、四角形ABCDが平行四辺形であるとき、次の問いに答えよ。
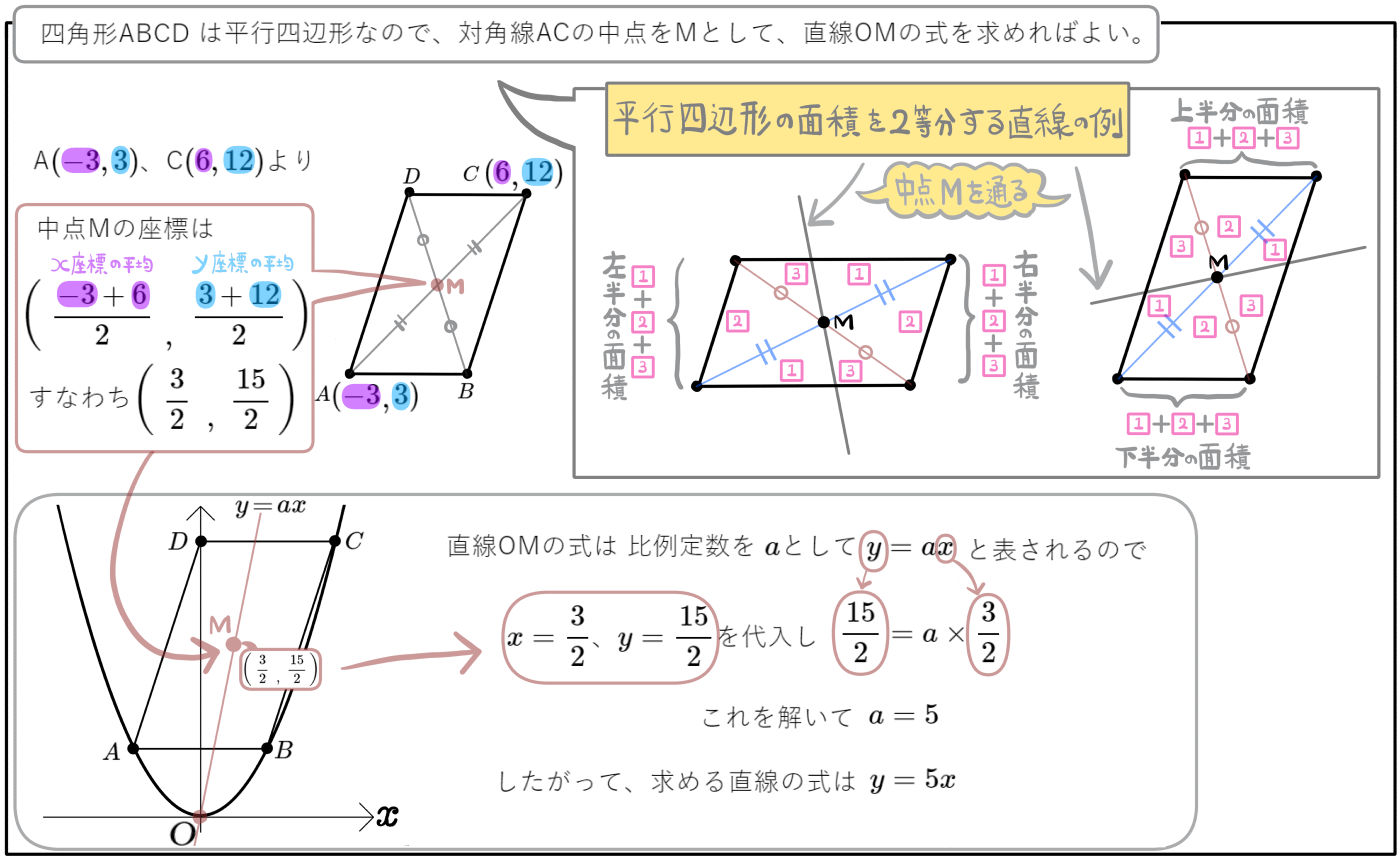
(1)四角形ABCDの面積を求めよ。


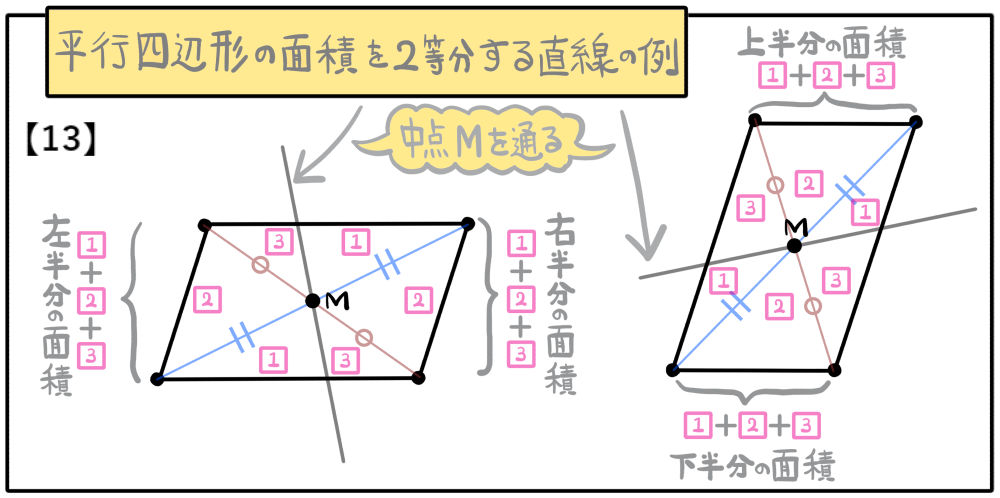
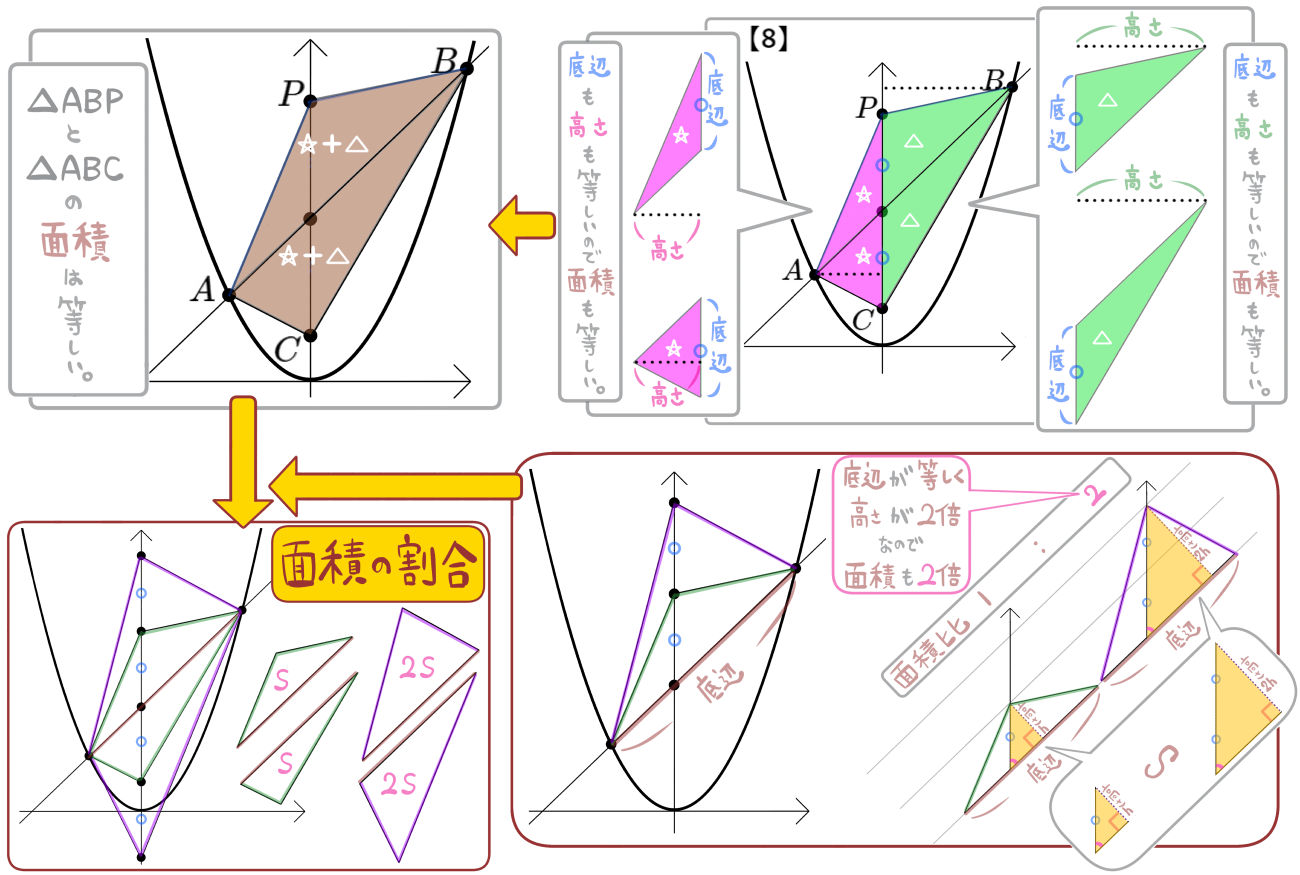
上下に別れた図形もともに1、2、3を合計した面積になり、上下の面積は等しくなります。

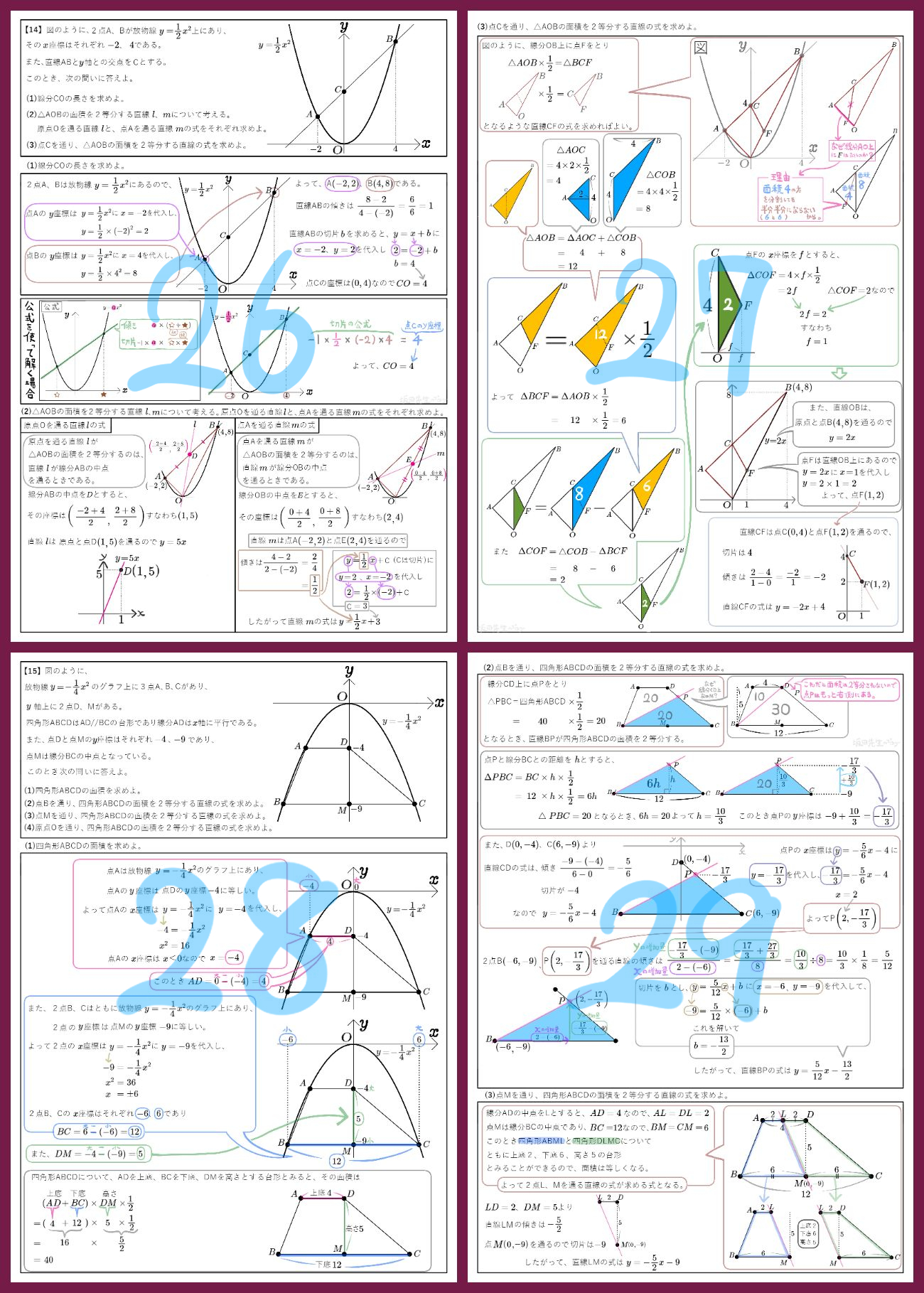
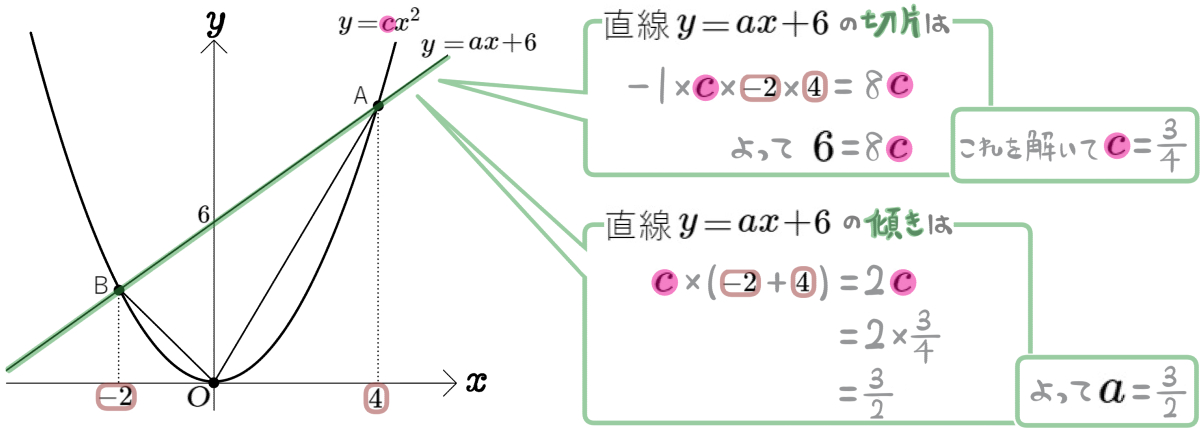
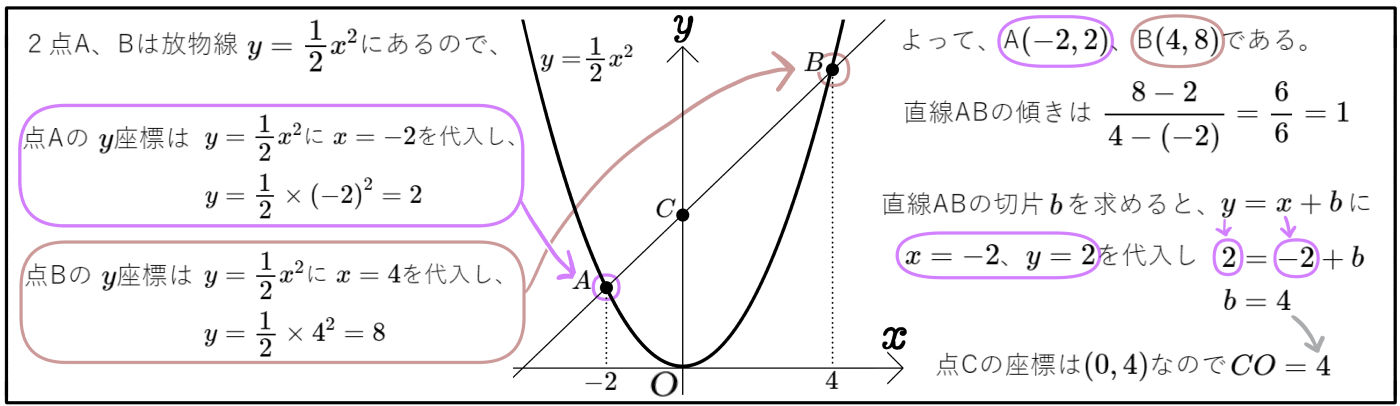
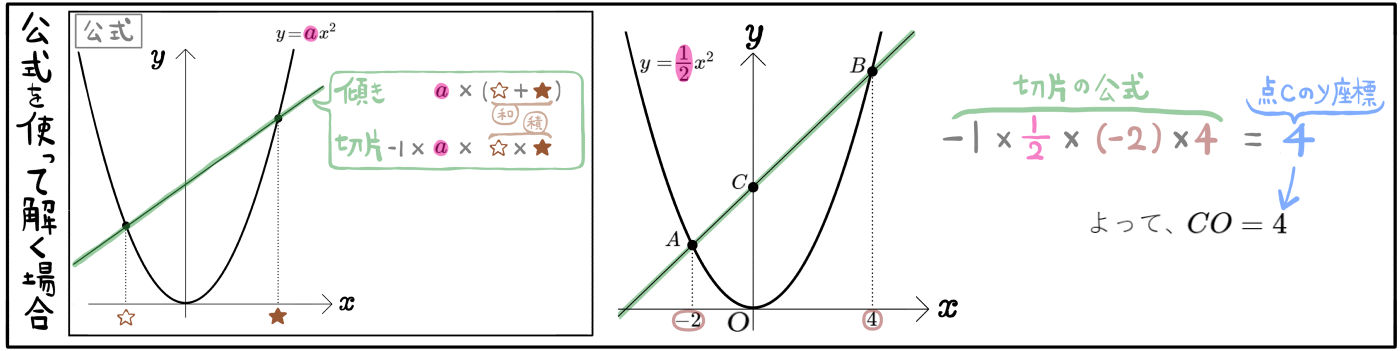
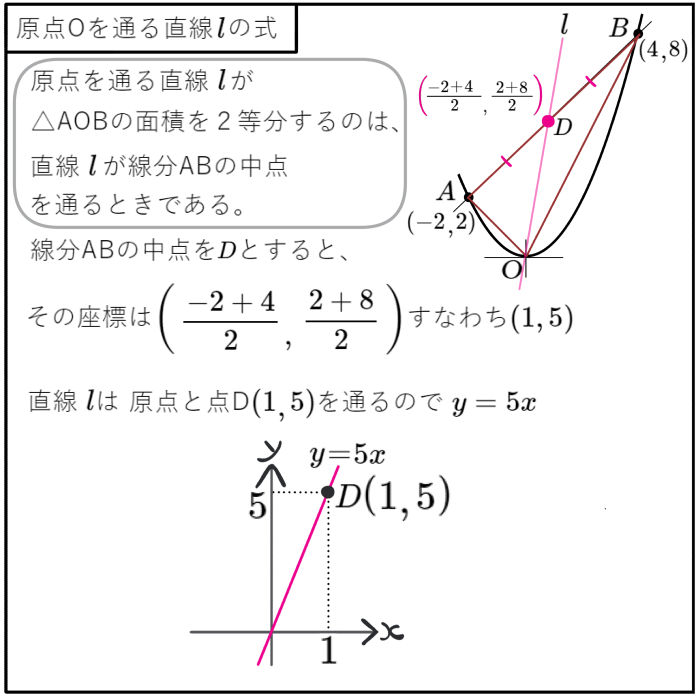
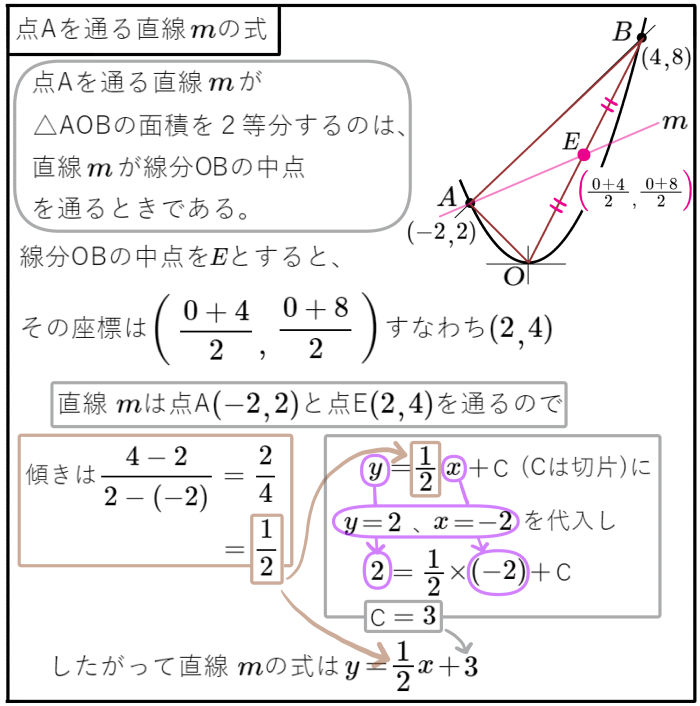
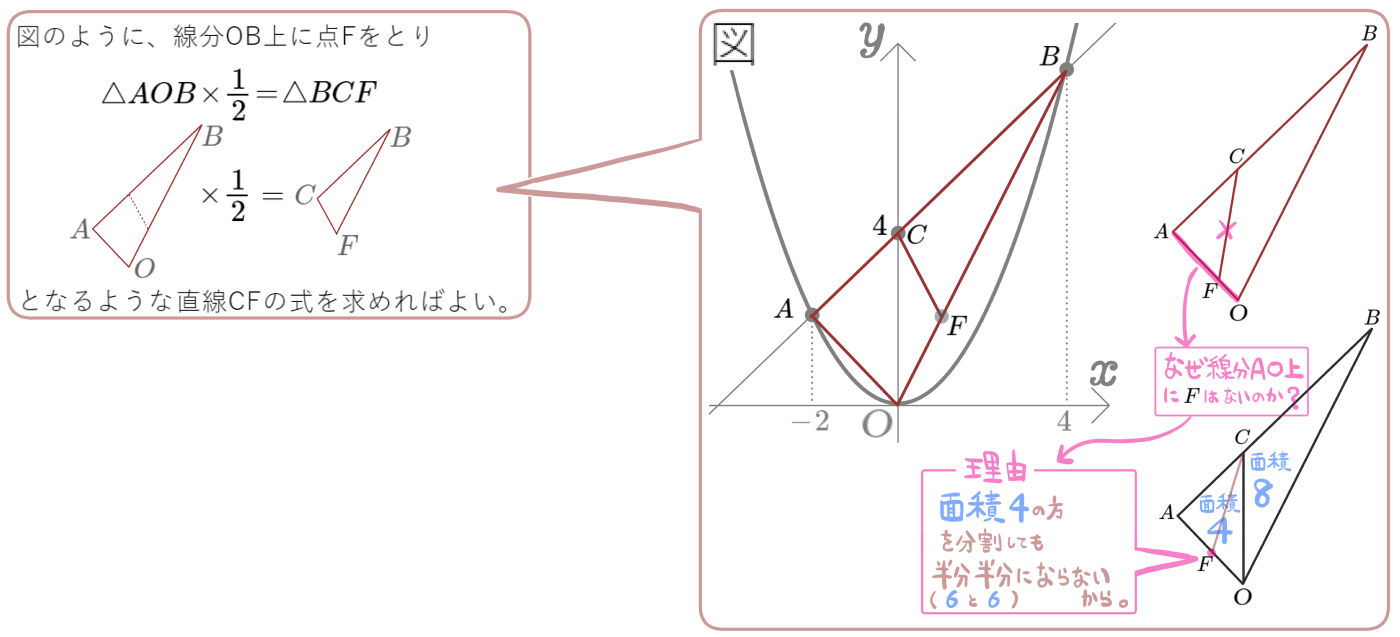
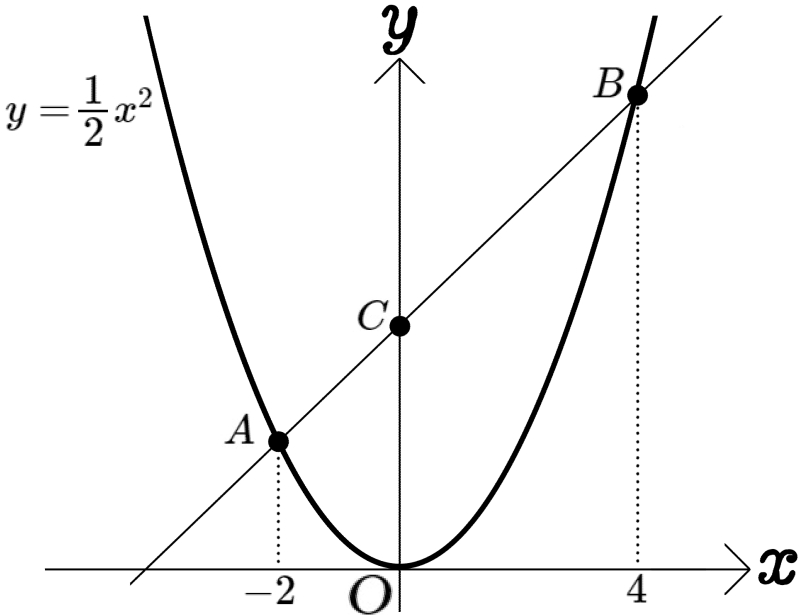 図のように、2点A、Bが放物線\(y=\dfrac{1}{2}x^{2}\)上にあり、その \(x\)座標はそれぞれ \(-2\)、 \(4\)である。また、直線ABと\(y\)軸との交点をCとする。このとき、次の問いに答えよ。
図のように、2点A、Bが放物線\(y=\dfrac{1}{2}x^{2}\)上にあり、その \(x\)座標はそれぞれ \(-2\)、 \(4\)である。また、直線ABと\(y\)軸との交点をCとする。このとき、次の問いに答えよ。
(1)線分COの長さを求めよ。
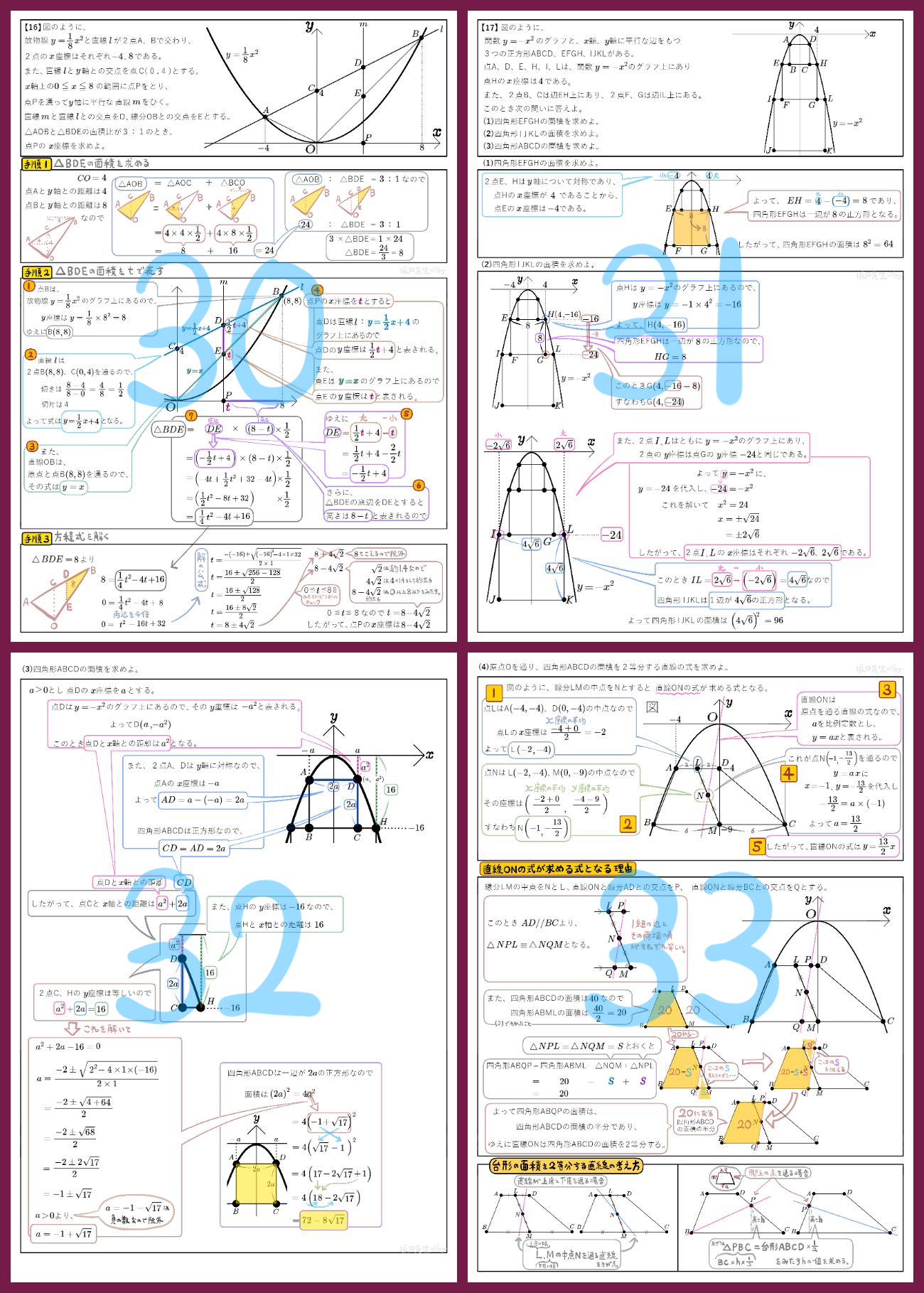
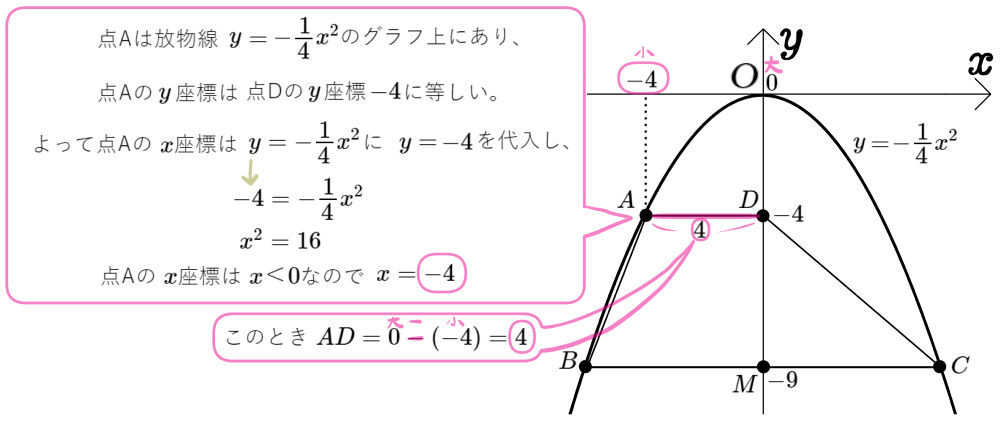
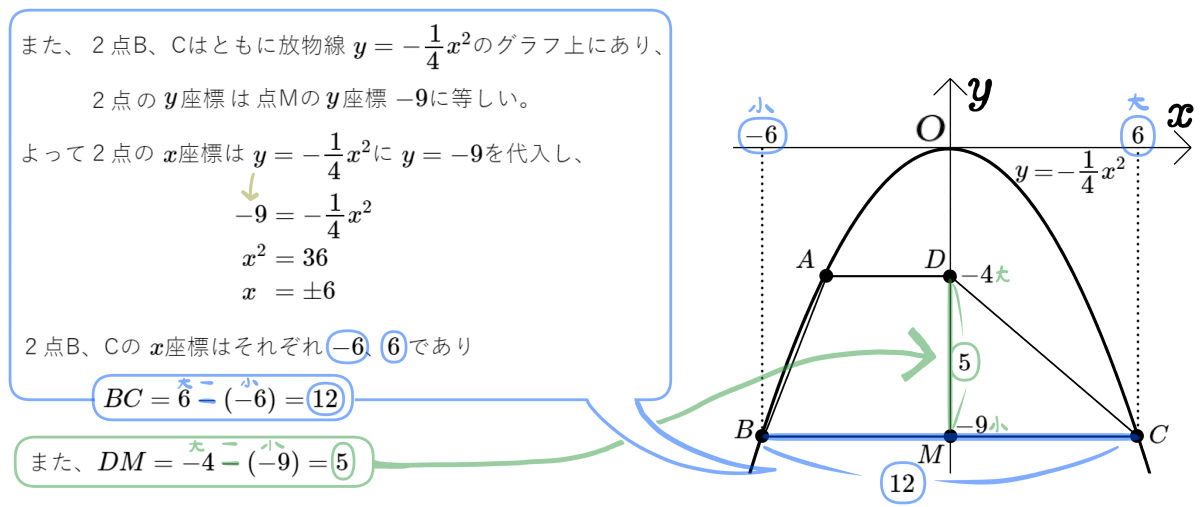
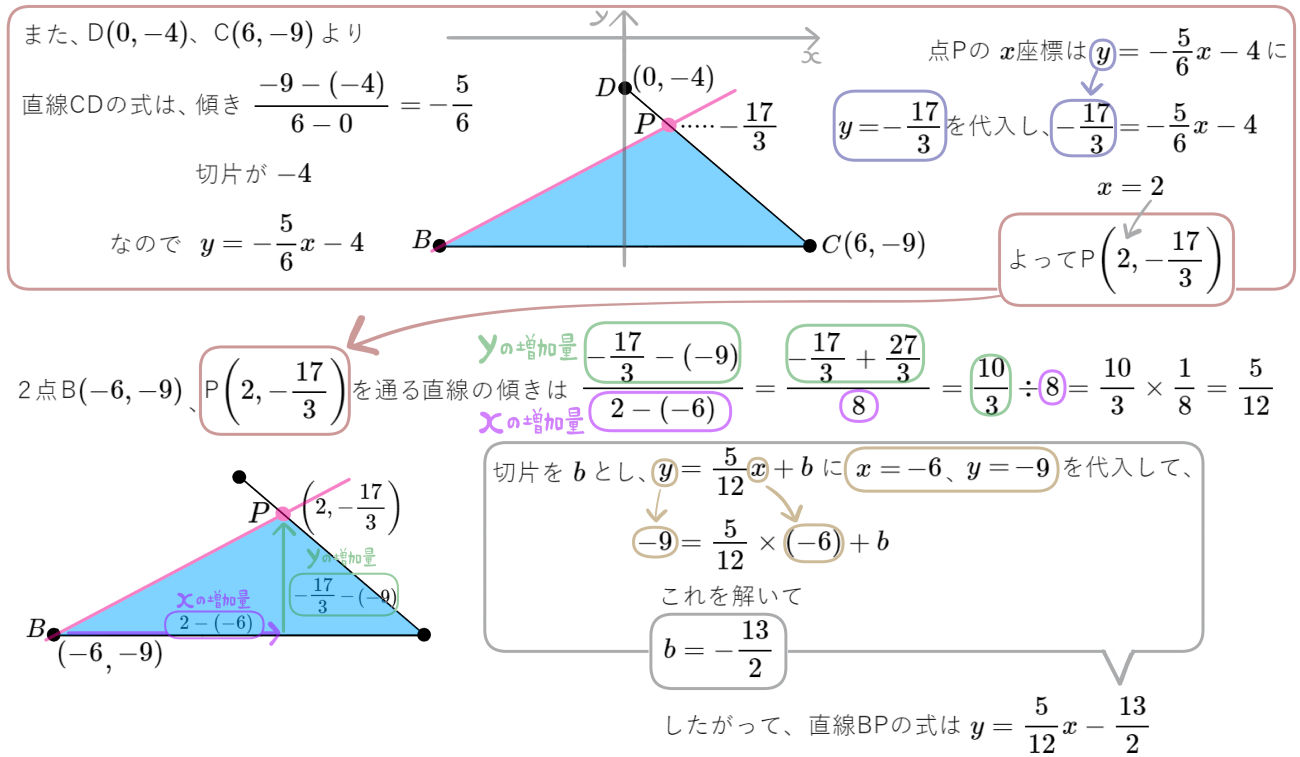
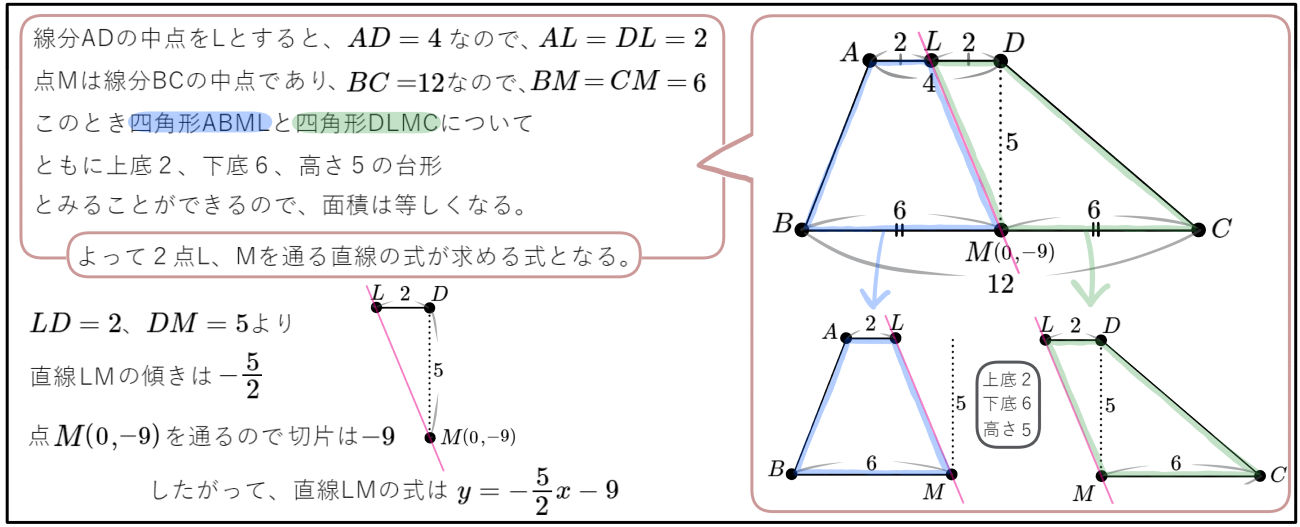
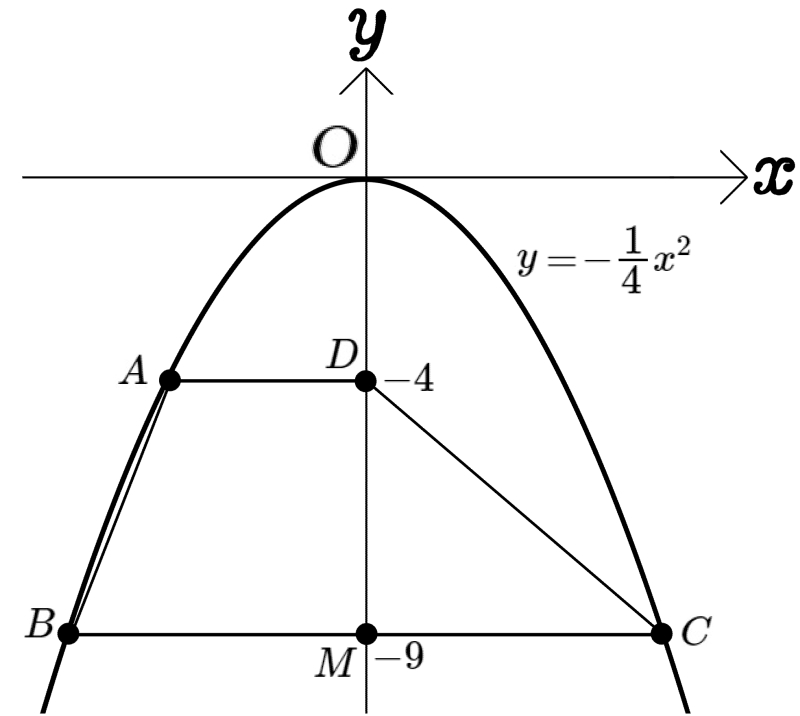 図のように、放物線\(y=-\dfrac{1}{4}x^{2}\)のグラフ上に3点A、B、Cがあり、\(y\)軸上に2点D、Mがある。四角形ABCDはAD//BCの台形であり線分ADは\(x\)軸に平行である。点Dと点Mの\(y\)座標はそれぞれ\(-4\)、\(-9\)であり、点Mは線分BCの中点となっている。このとき次の問いに答えよ。
図のように、放物線\(y=-\dfrac{1}{4}x^{2}\)のグラフ上に3点A、B、Cがあり、\(y\)軸上に2点D、Mがある。四角形ABCDはAD//BCの台形であり線分ADは\(x\)軸に平行である。点Dと点Mの\(y\)座標はそれぞれ\(-4\)、\(-9\)であり、点Mは線分BCの中点となっている。このとき次の問いに答えよ。
(1)四角形ABCDの面積を求めよ。






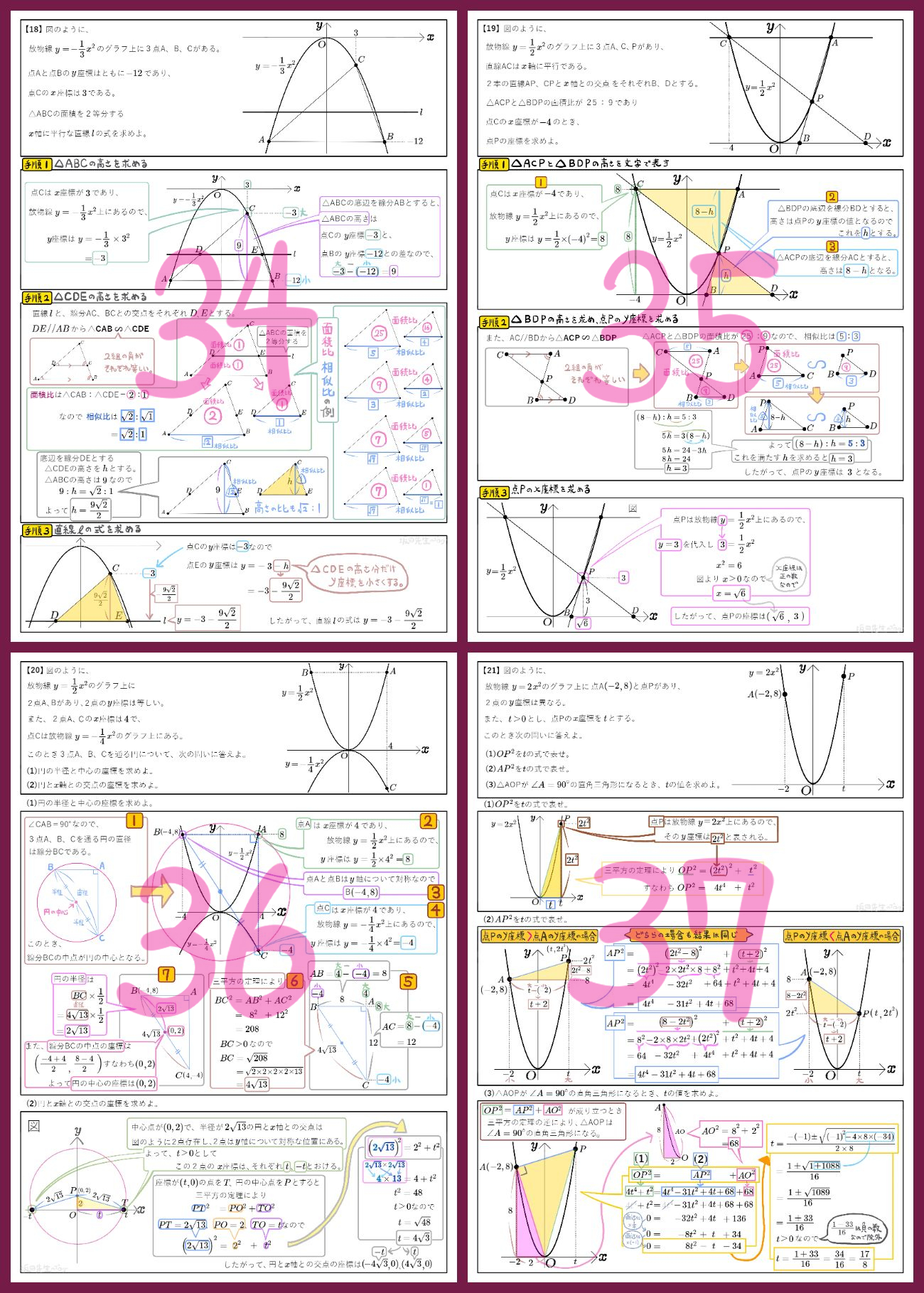
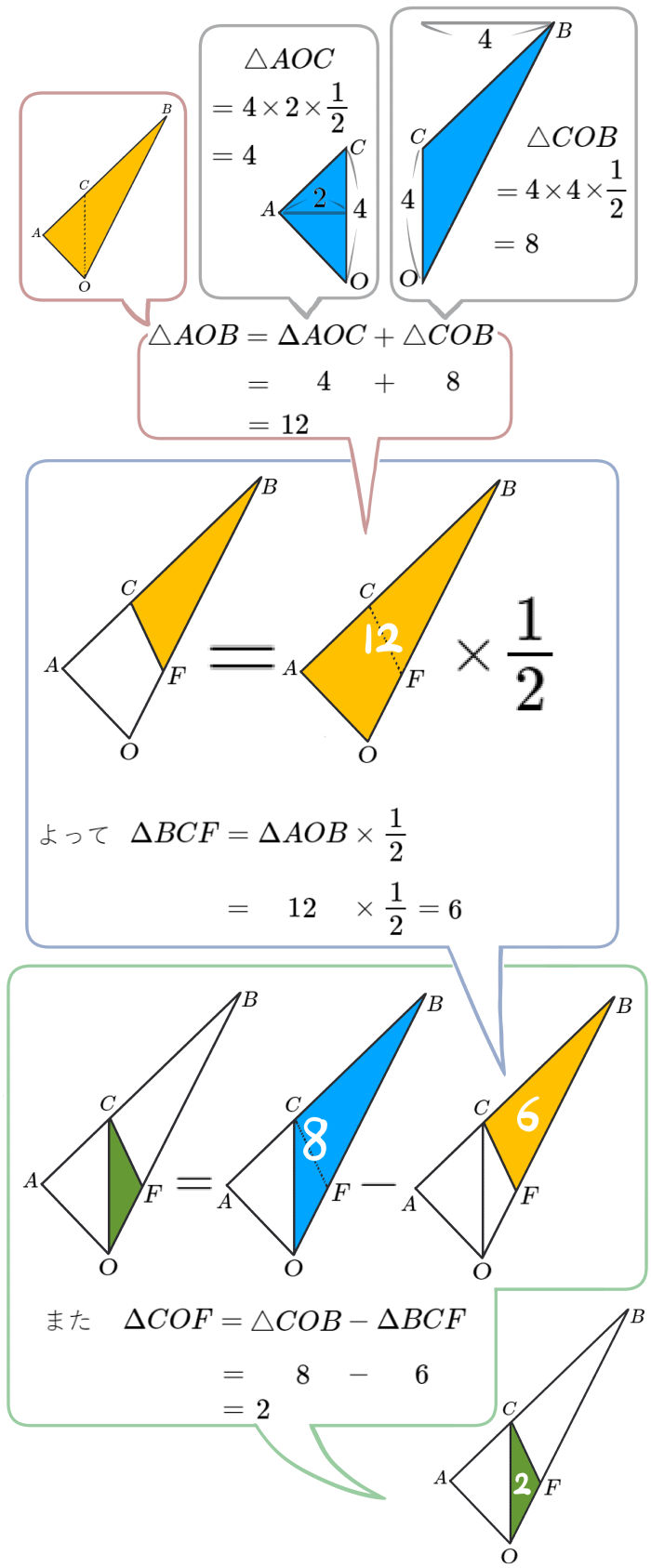
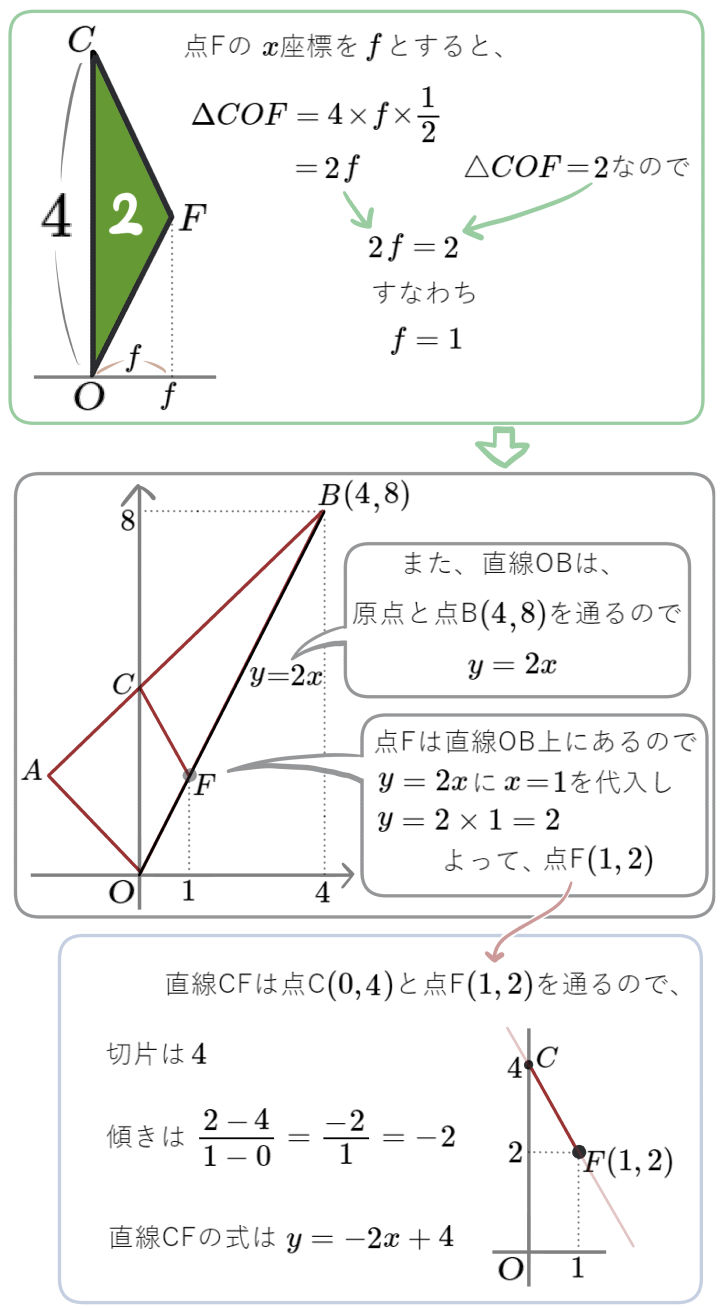
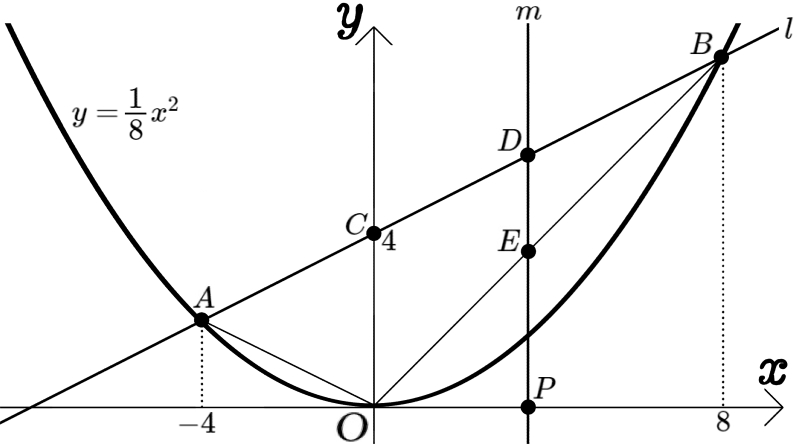 図のように、放物線\(y=\dfrac{1}{8}x^{2}\)と直線 \(l\)が2点A、Bで交わり、2点の \(x\)座標はそれぞれ\(-4\)、\(8\)である。また、直線 \(l\)と\(y\)軸との交点を点\(C( 0 , 4 )\)とする。\(x\)軸上の\(0\leqq x\leqq 8\) の範囲に点Pをとり、点Pを通って\(y\)軸に平行な直線 \(m\)をひく。
図のように、放物線\(y=\dfrac{1}{8}x^{2}\)と直線 \(l\)が2点A、Bで交わり、2点の \(x\)座標はそれぞれ\(-4\)、\(8\)である。また、直線 \(l\)と\(y\)軸との交点を点\(C( 0 , 4 )\)とする。\(x\)軸上の\(0\leqq x\leqq 8\) の範囲に点Pをとり、点Pを通って\(y\)軸に平行な直線 \(m\)をひく。
直線 \(m\)と直線 \(l\)との交点をD、直線 \(m\)と線分OBとの交点をEとする。
△AOBと△BDEの面積比が3:1のとき、点Pの \(x\)座標を求めよ。
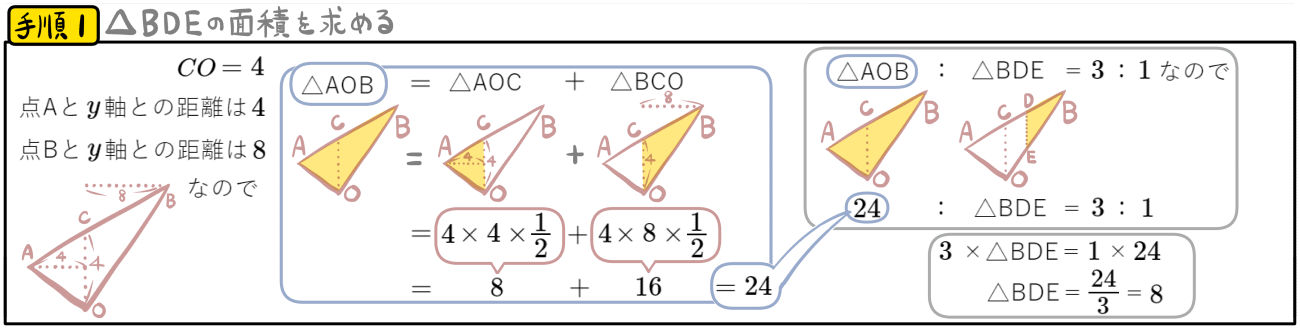
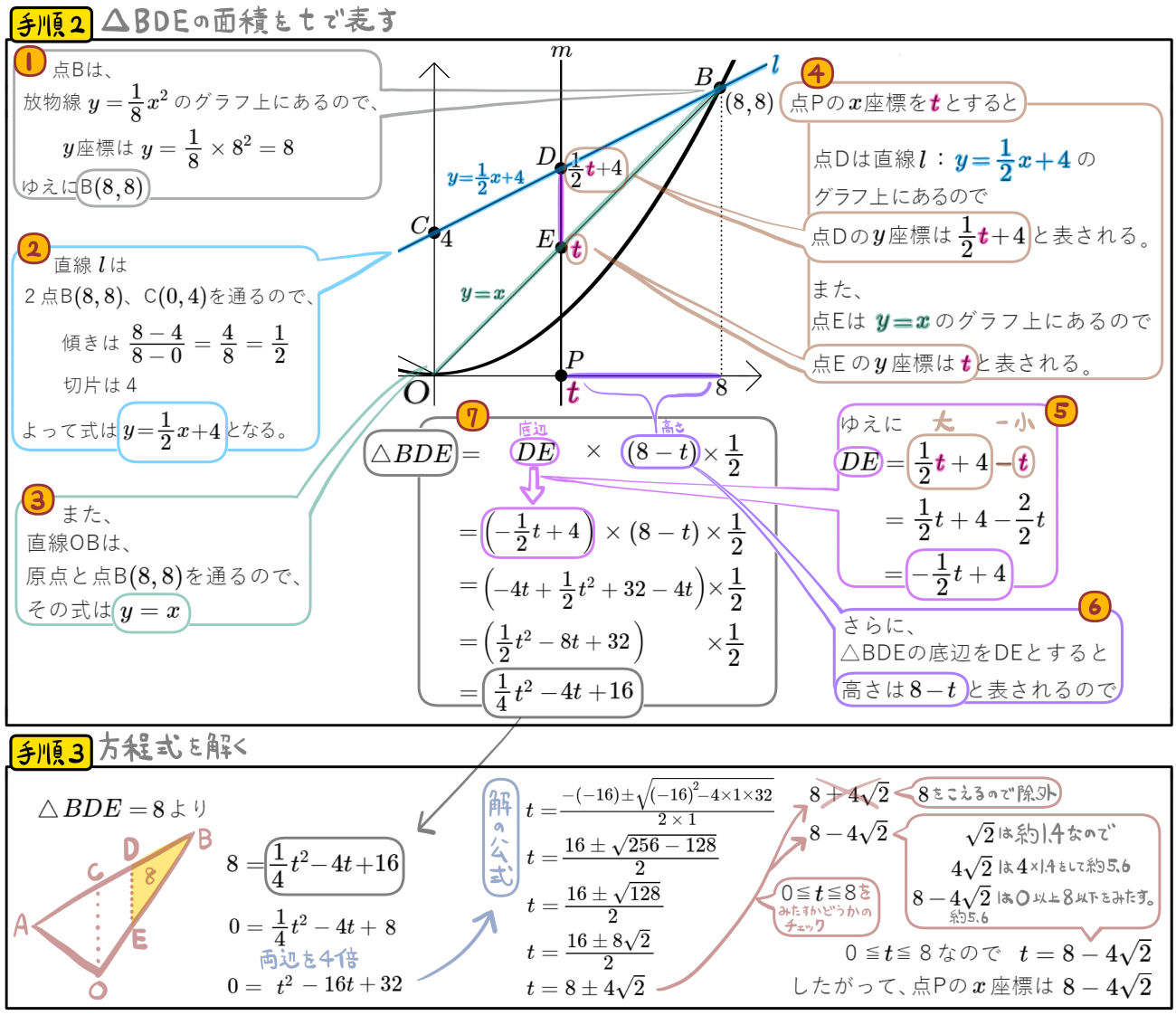
問題にある条件から、まず△AOBの面積は求めることができそうだ。さらに△AOBと△BDEの面積比が3:1なので、△BDEの面積も求めることができる。じゃあ、その面積になるために、点Pの\(x\)座標が何であればいいかを考えればいいわけだ。
【さらにここまで発想できるとベリーグッド】
点Pの\(x\)座標を文字tでおいて、△BDEの面積をtを使った式で表すことができれば、△BDEの面積はわかっているわけだから、方程式を作ってtを求めることができそうだ。
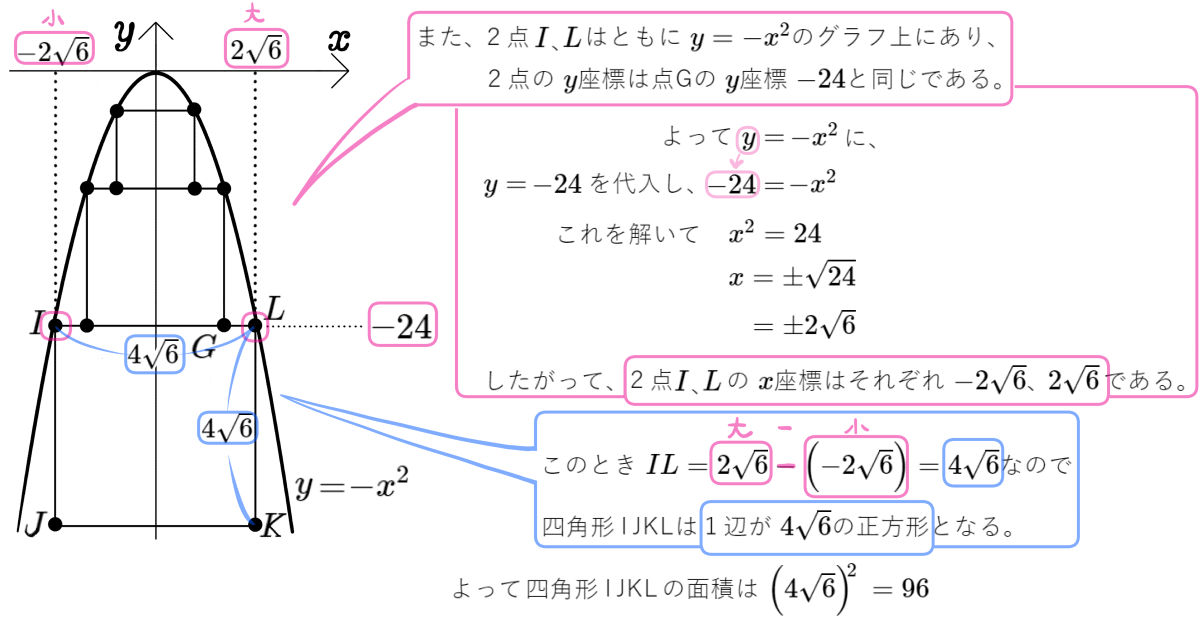
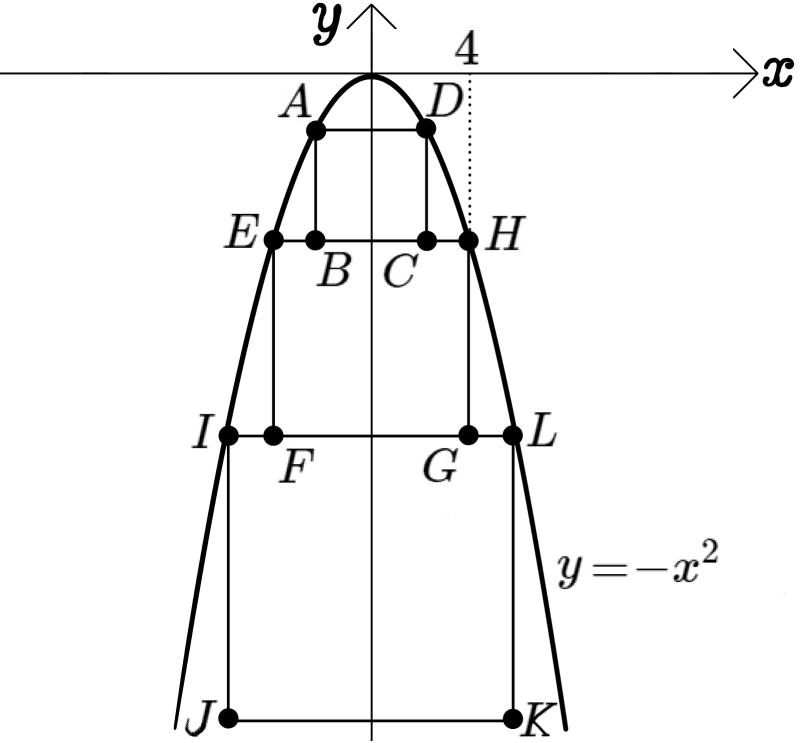 図のように、関数 \(y=-x^{2}\)のグラフと、\(x\)軸、\(y\)軸に平行な辺をもつ3つの正方形ABCD、EFGH、IJKLがある。
図のように、関数 \(y=-x^{2}\)のグラフと、\(x\)軸、\(y\)軸に平行な辺をもつ3つの正方形ABCD、EFGH、IJKLがある。
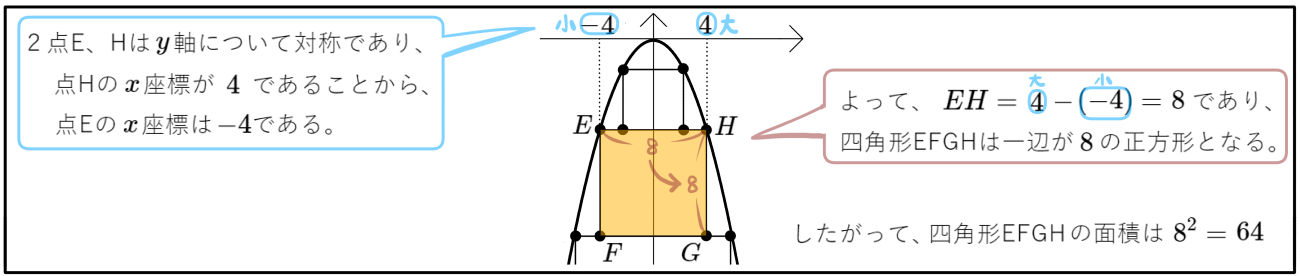
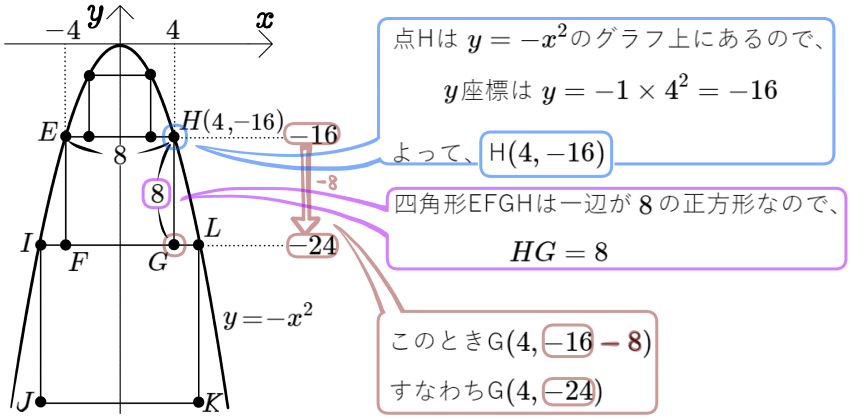
点A、D、E、H、I、Lは、関数 \(y=-x^{2}\)のグラフ上にあり、点Hの \(x\)座標は \(4\)である。また、2点B、Cは辺EH上にあり、2点F、Gは辺IL上にある。
このとき次の問いに答えよ。
(1)四角形EFGHの面積を求めよ。
2次関数の標準~難問|融合問題など高校入試対策用



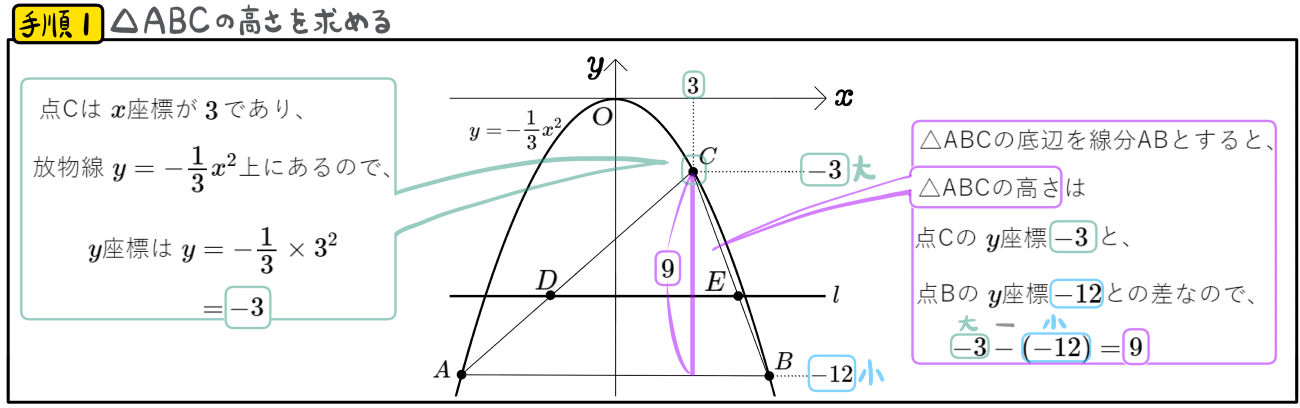
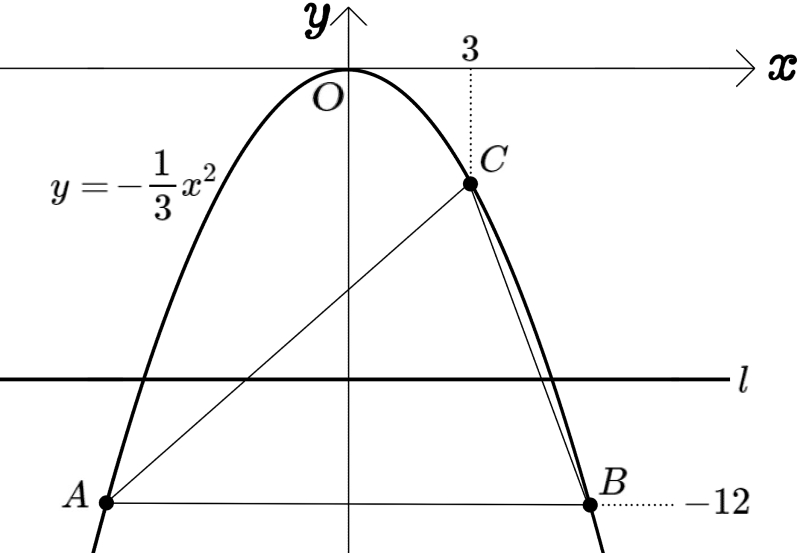 図のように、放物線\(y=-\dfrac{1}{3}x^{2}\)のグラフ上に3点A、B、Cがある。
図のように、放物線\(y=-\dfrac{1}{3}x^{2}\)のグラフ上に3点A、B、Cがある。
点Aと点Bの \(y\)座標はともに \(-12\)であり、点Cの \(x\)座標は \(3\)である。
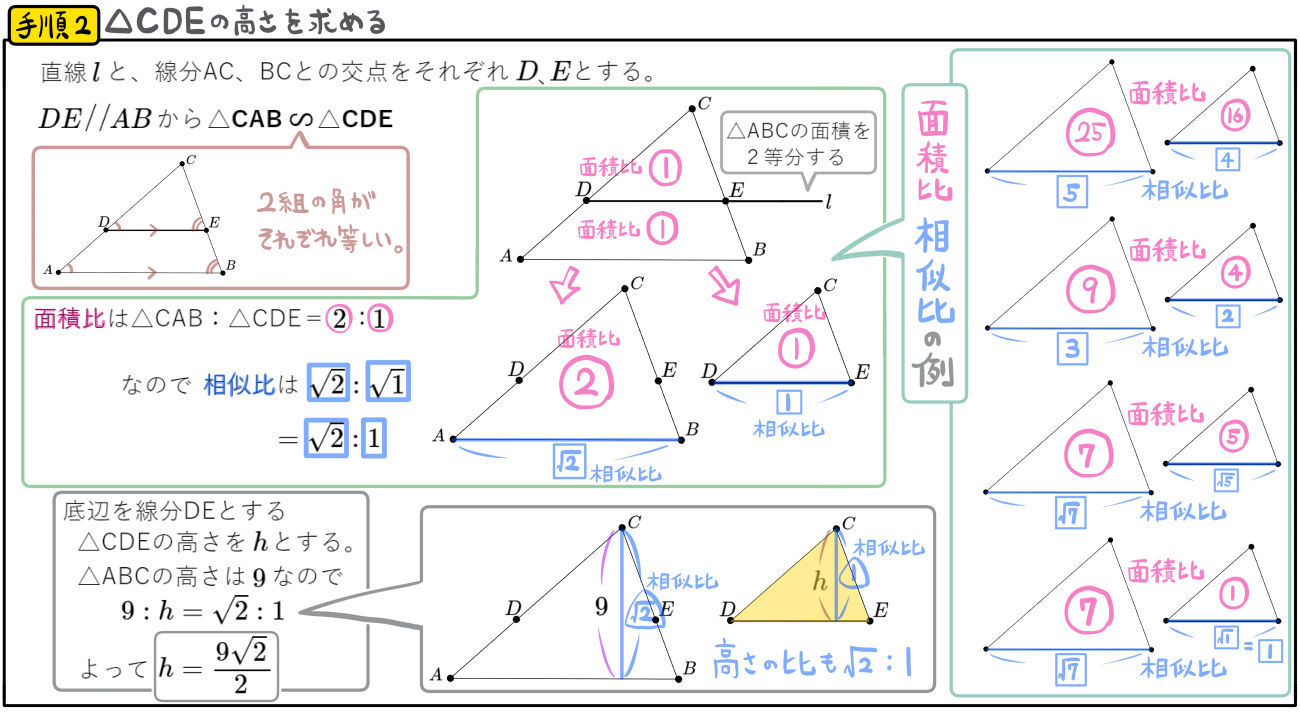
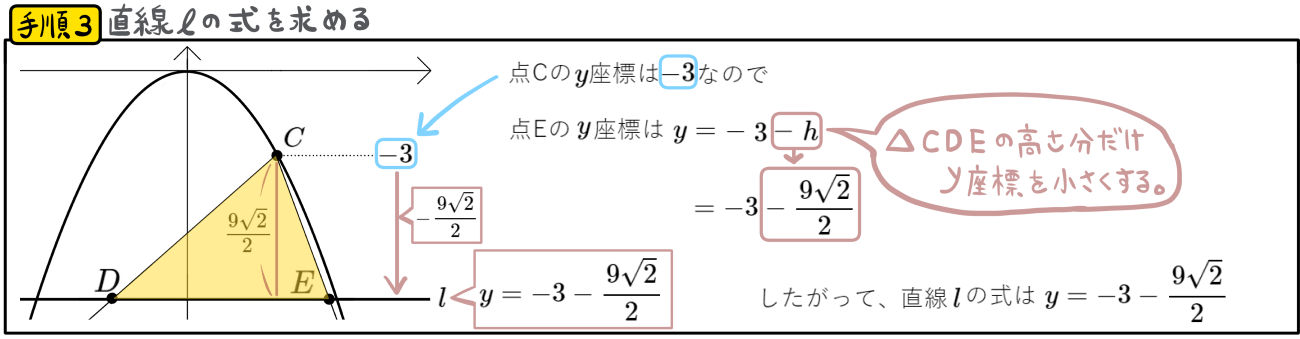
△ABCの面積を2等分する\(x\)軸に平行な直線 \(l\)の式を求めよ。
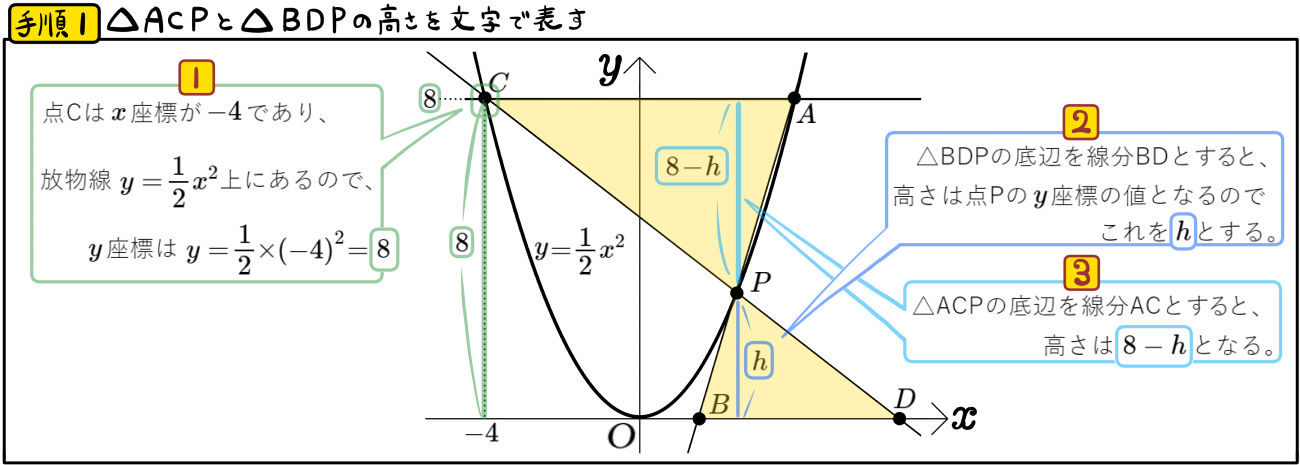
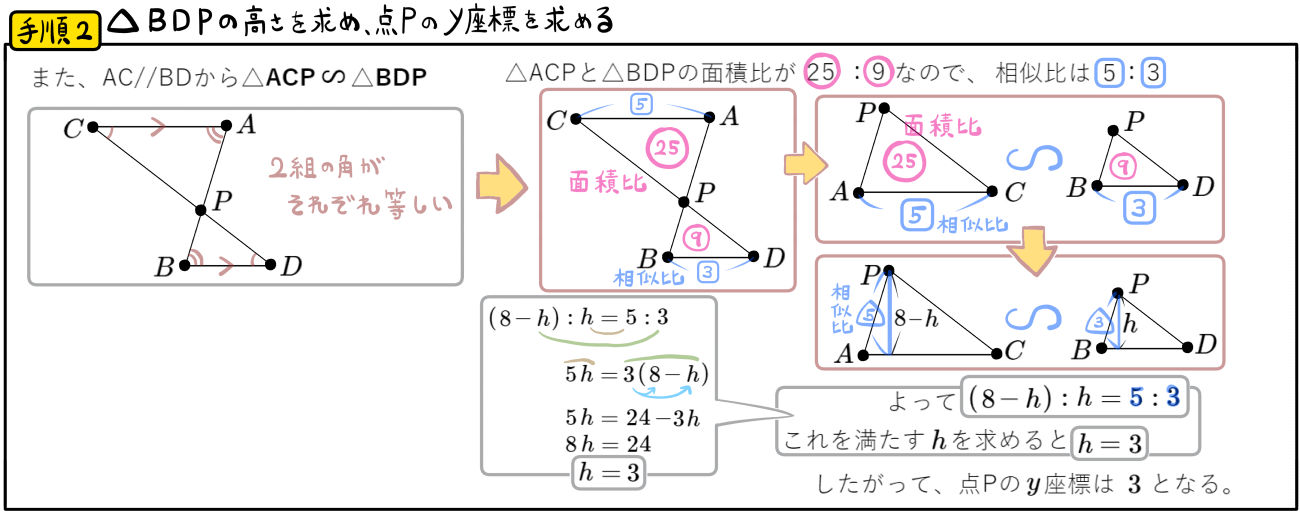
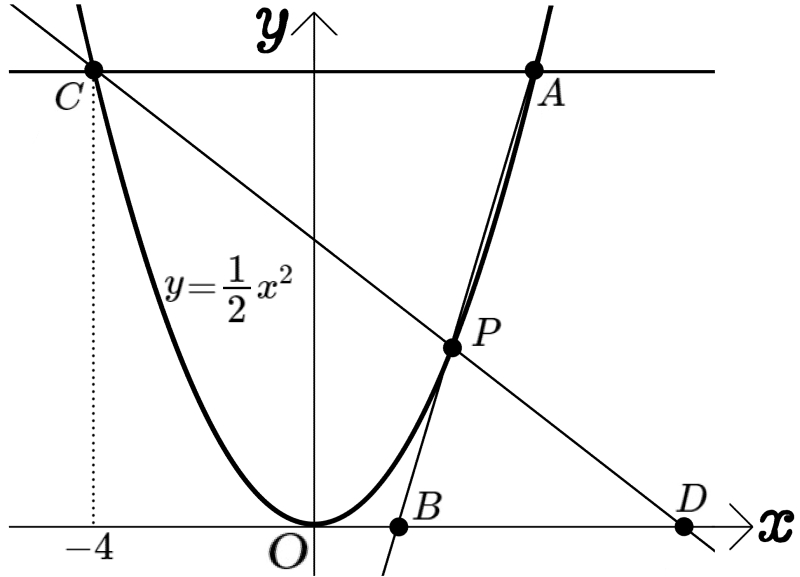 図のように、放物線 \(y=\dfrac{1}{2}x^{2}\)のグラフ上に3点A、C、Pがあり、直線ACは \(x\)軸に平行である。
図のように、放物線 \(y=\dfrac{1}{2}x^{2}\)のグラフ上に3点A、C、Pがあり、直線ACは \(x\)軸に平行である。
2本の直線AP、CPと \(x\)軸との交点をそれぞれB、Dとする。
△ACPと△BDPの面積比が25:9であり点Cの \(x\)座標が \(-4\)のとき、点Pの座標を求めよ。

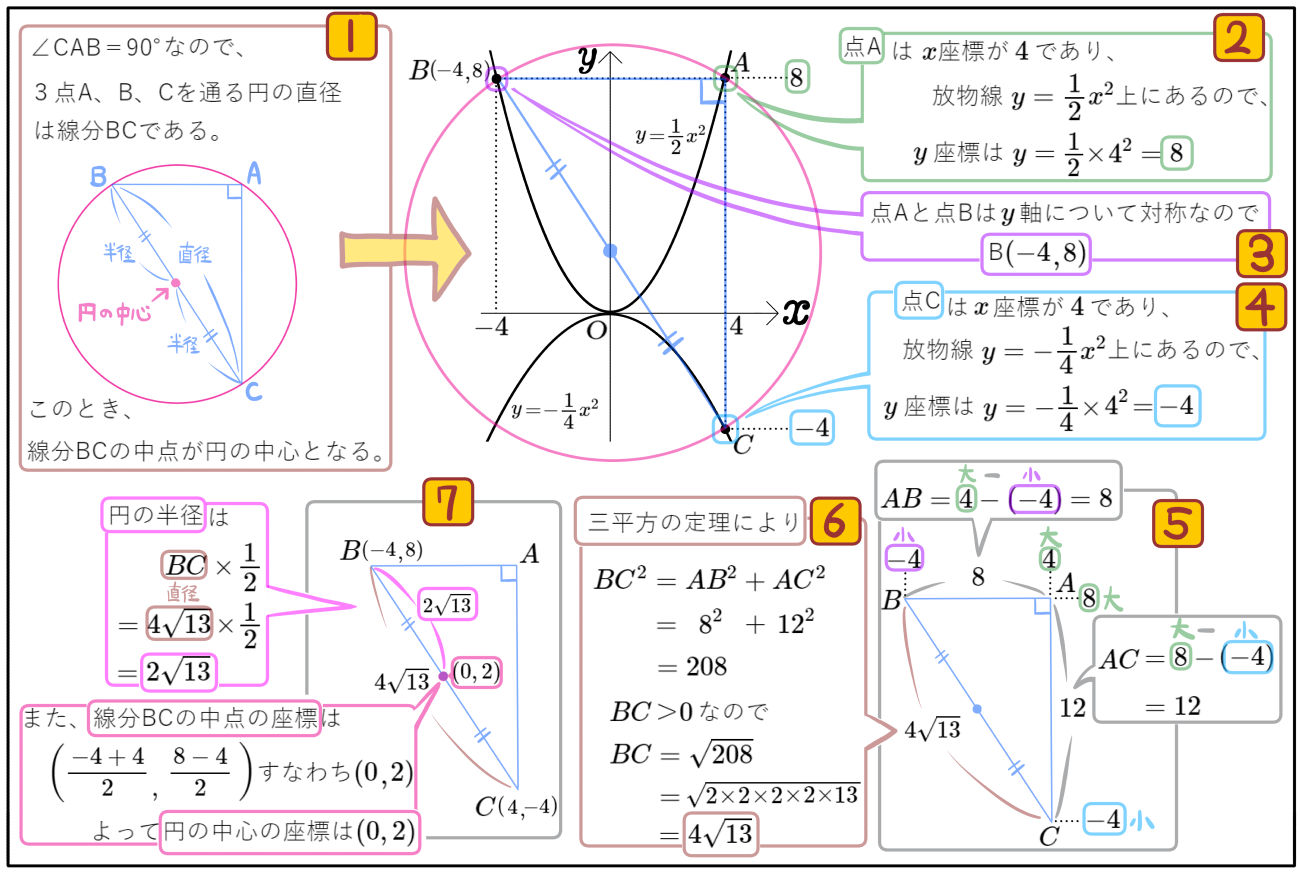
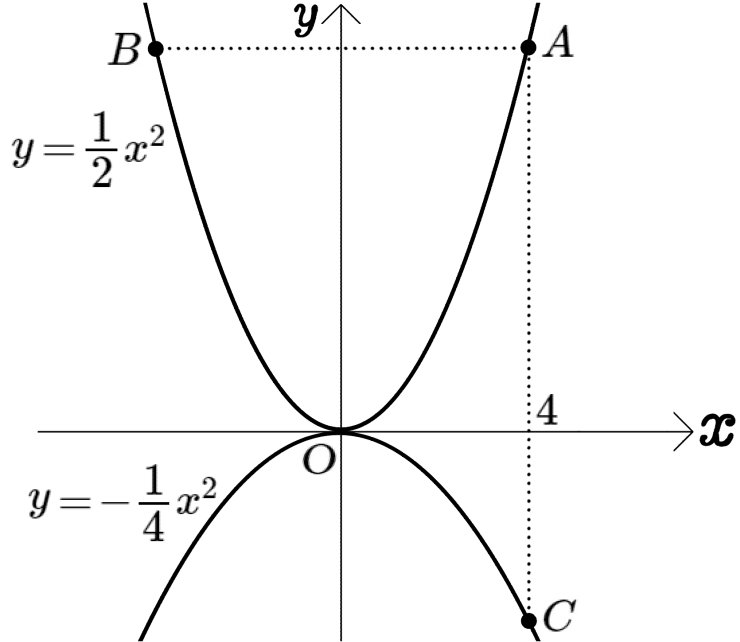 図のように、放物線 \(y=\dfrac{1}{2}x^{2}\)のグラフ上に2点A、Bがあり、2点の\(y\)座標は等しい。
図のように、放物線 \(y=\dfrac{1}{2}x^{2}\)のグラフ上に2点A、Bがあり、2点の\(y\)座標は等しい。
また、2点A、Cの\(x\)座標は4で、点Cは放物線 \(y=-\dfrac{1}{4}x^{2}\)のグラフ上にある。
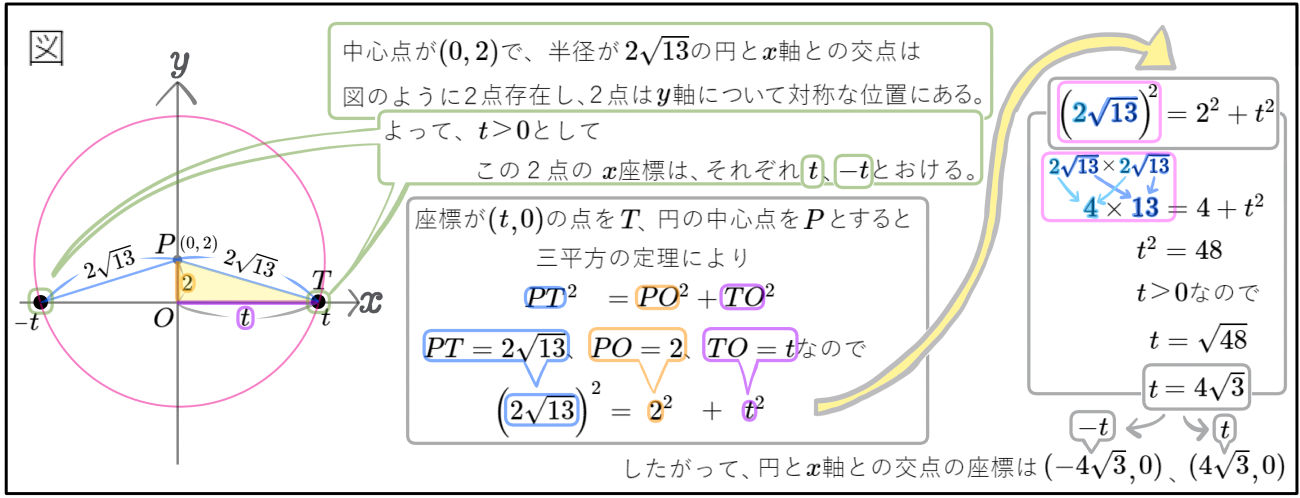
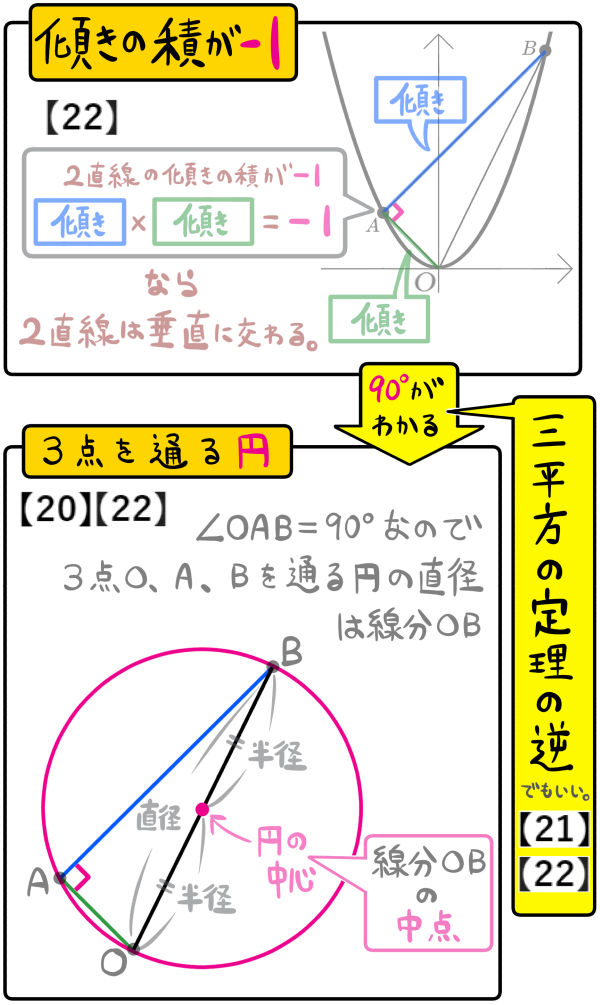
このとき3点A、B、Cを通る円について、次の問いに答えよ。
(1)円の半径と中心の座標を求めよ。
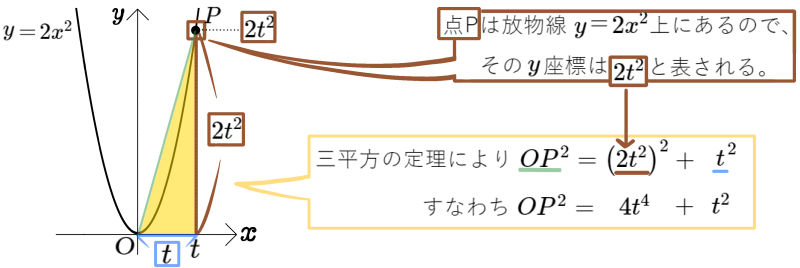
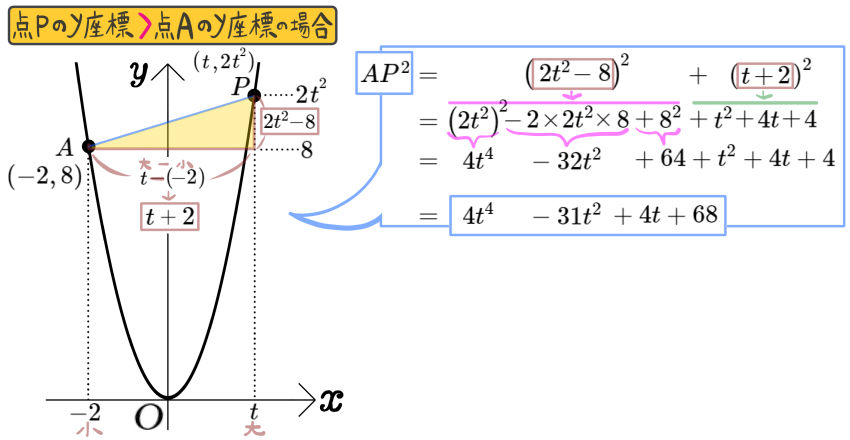
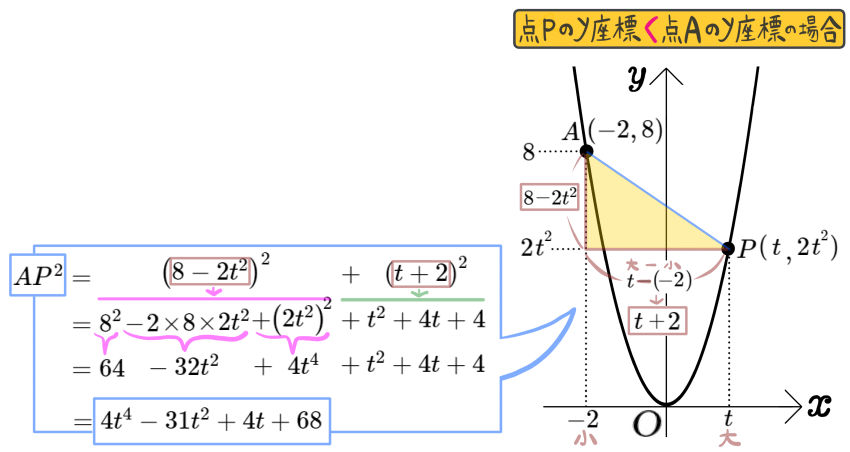
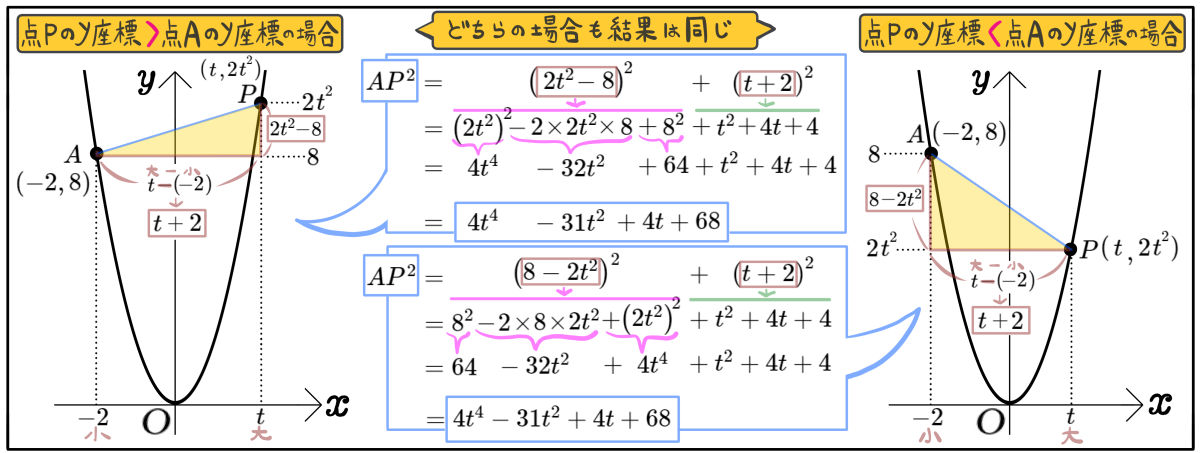
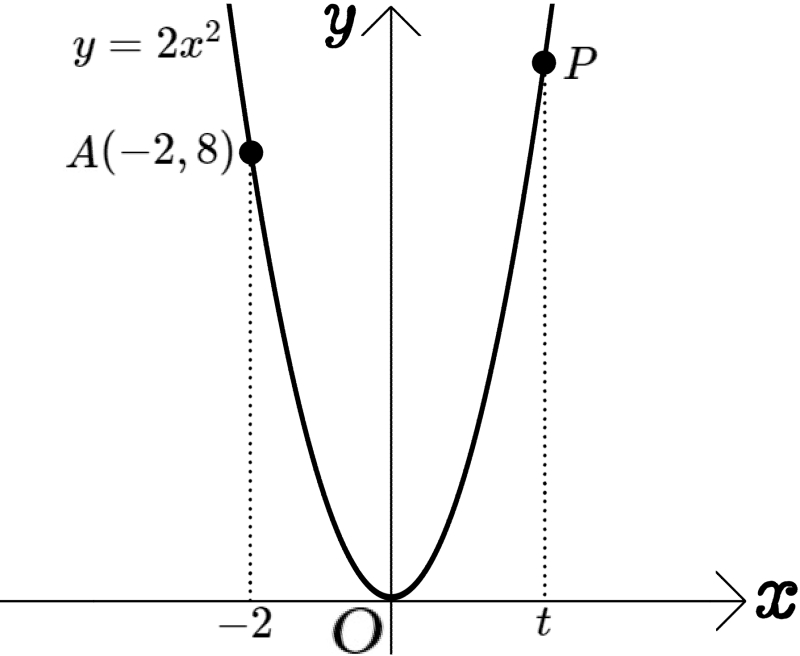 図のように、放物線 \(y=2x^{2}\)のグラフ上に点A\(( -2 , 8 )\)と点Pがあり、2点の\(y\)座標は異なる。
図のように、放物線 \(y=2x^{2}\)のグラフ上に点A\(( -2 , 8 )\)と点Pがあり、2点の\(y\)座標は異なる。
また、 \(t>0\)とし、点Pの\(x\)座標を \(t\)とする。
このとき次の問いに答えよ。
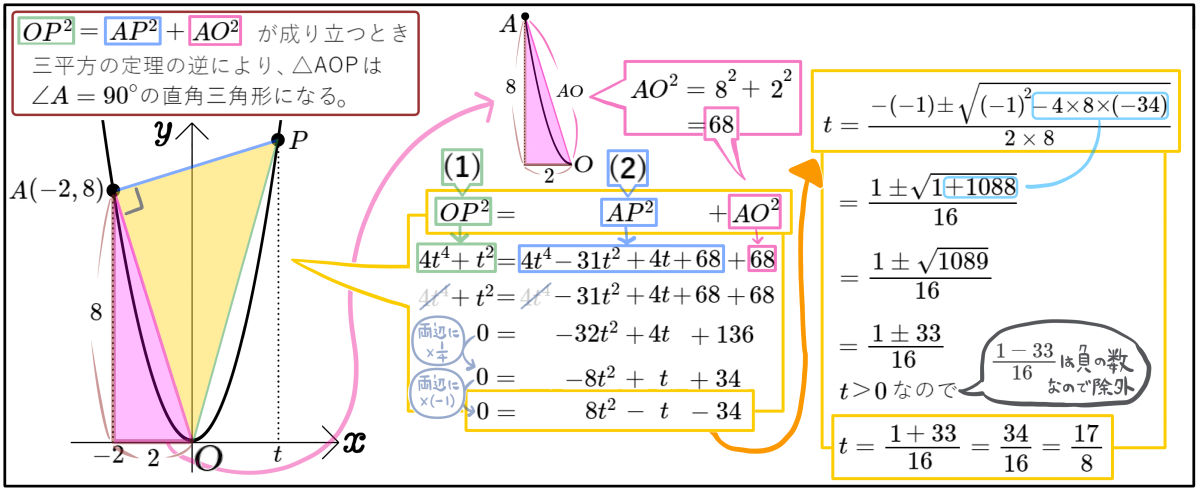
(1)\(OP^{2}\)を\(t\)の式で表せ。
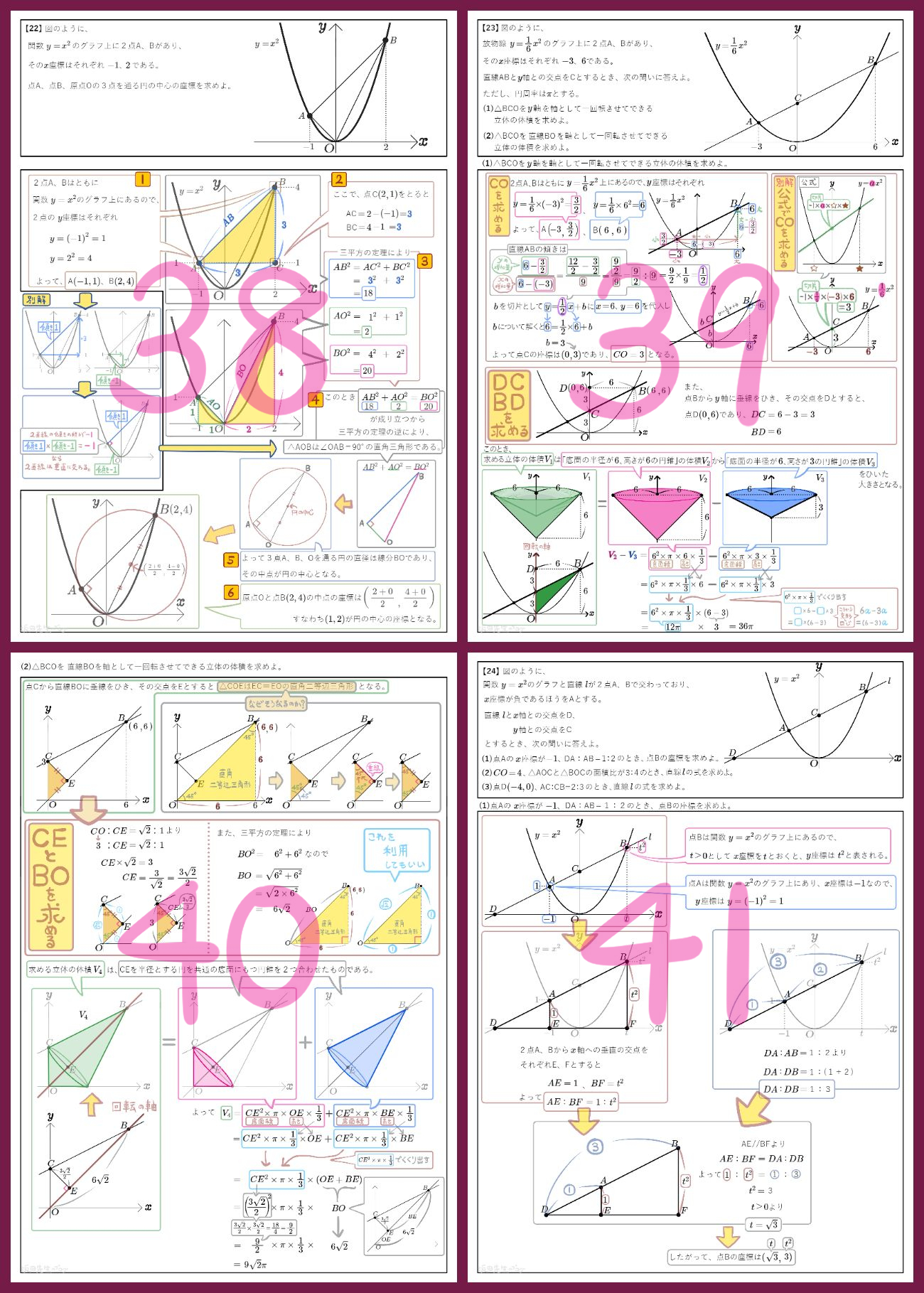
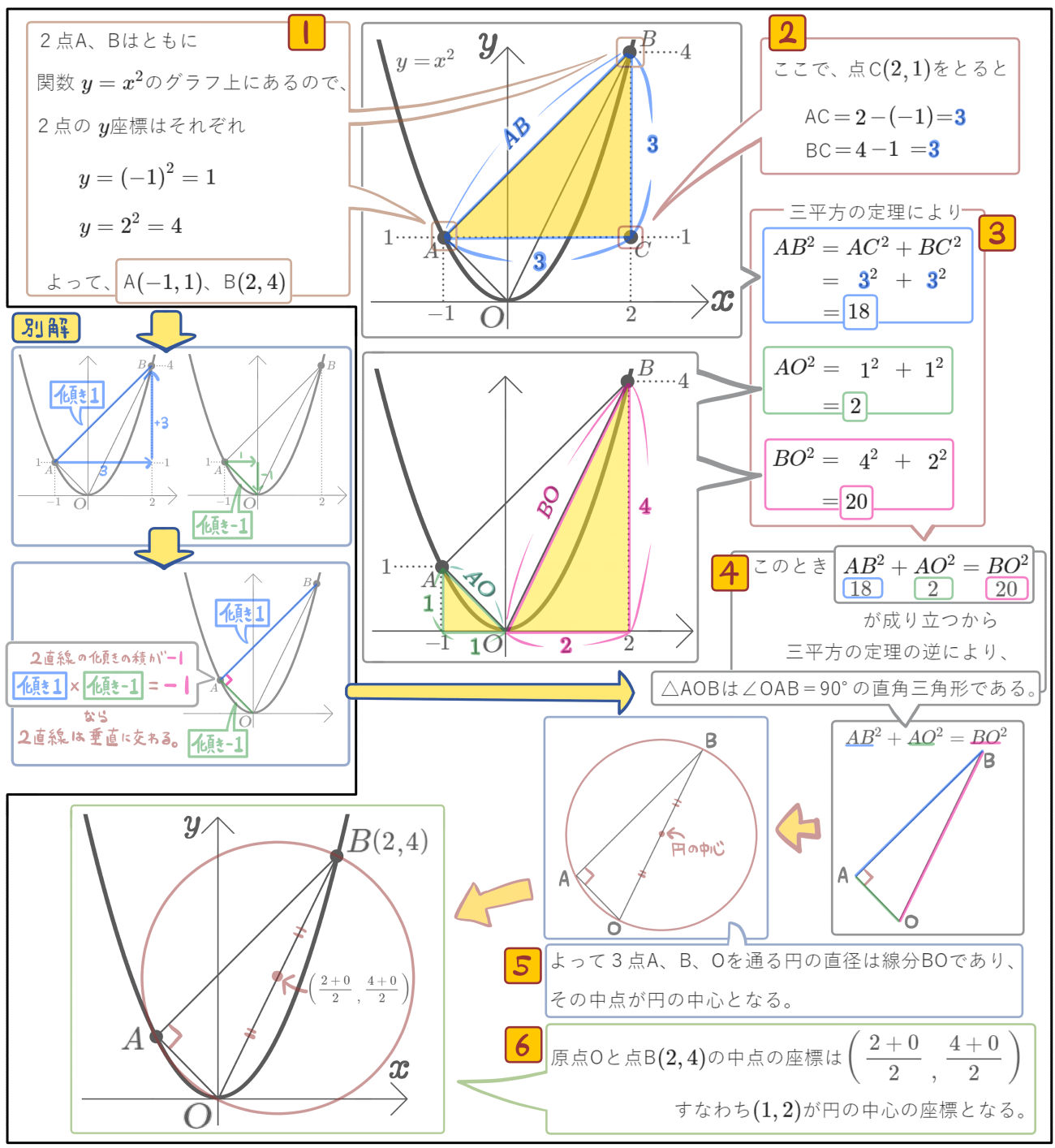
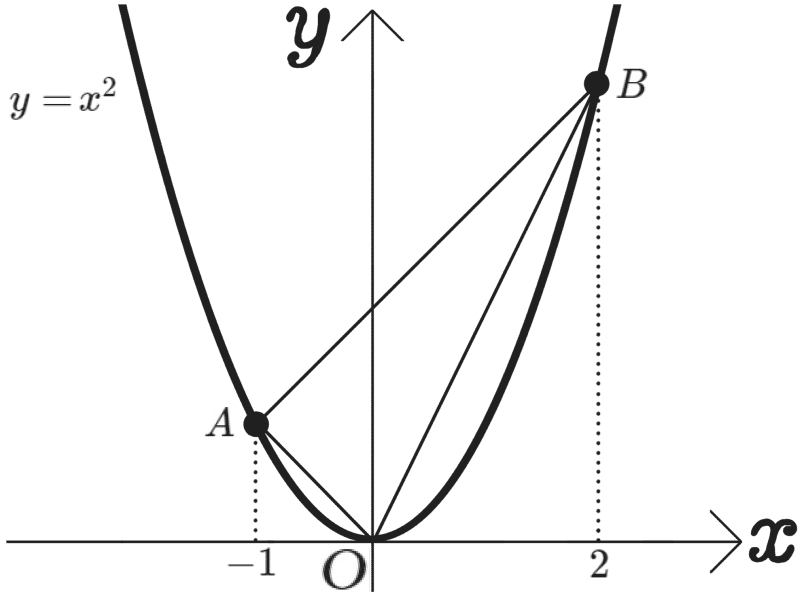 図のように、関数 \(y=x^{2}\)のグラフ上に2点A、Bがあり、その\(x\)座標はそれぞれ \(-1\)、\(2\)である。
図のように、関数 \(y=x^{2}\)のグラフ上に2点A、Bがあり、その\(x\)座標はそれぞれ \(-1\)、\(2\)である。
点A、点B、原点Oの3点を通る円の中心の座標を求めよ。
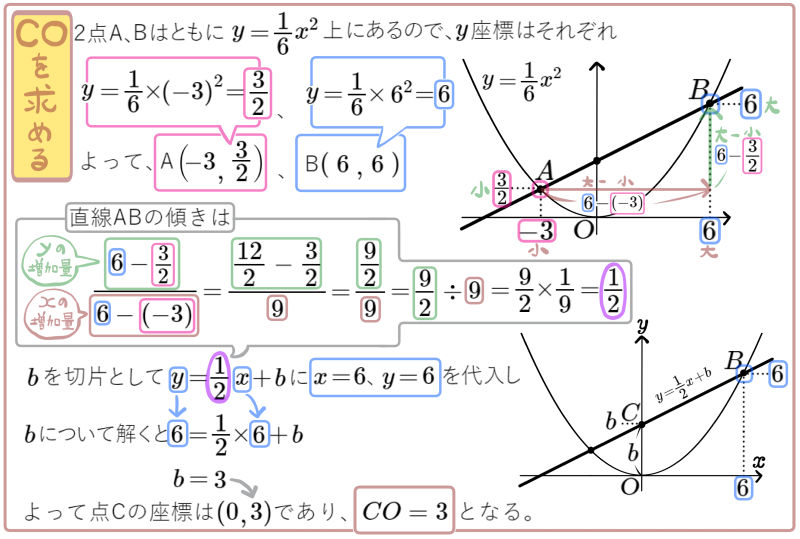
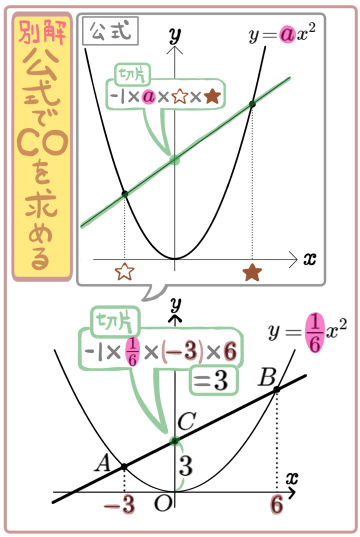
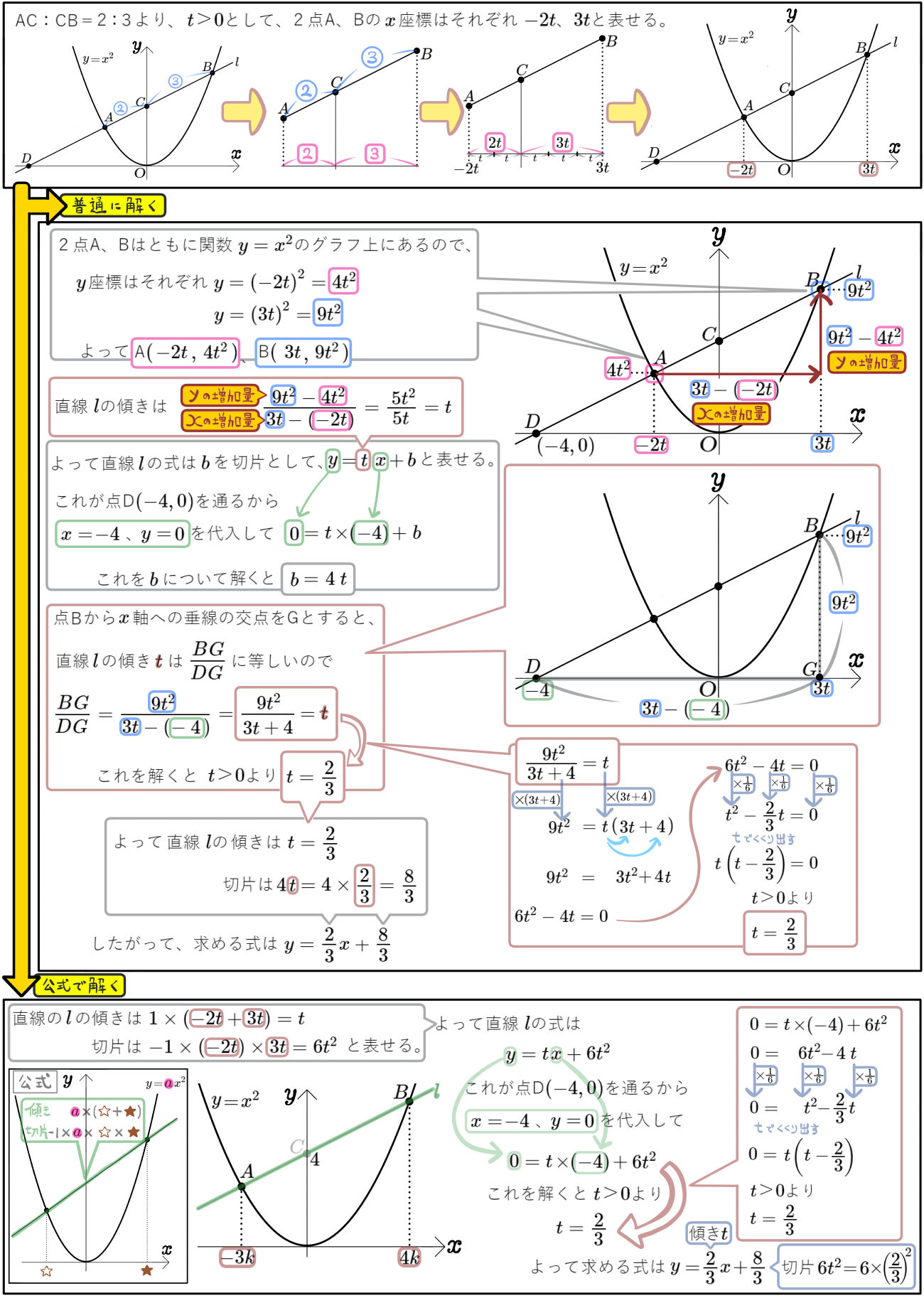
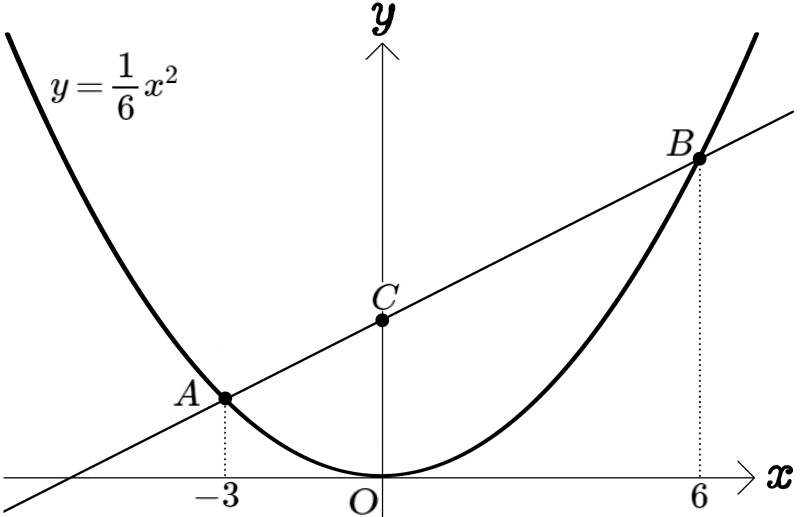 図のように、放物線 \(y=\dfrac{1}{6}x^{2}\)のグラフ上に2点A、Bがあり、その\(x\)座標はそれぞれ \(-3\)、\(6\)である。
図のように、放物線 \(y=\dfrac{1}{6}x^{2}\)のグラフ上に2点A、Bがあり、その\(x\)座標はそれぞれ \(-3\)、\(6\)である。
直線ABと\(y\)軸との交点をCとするとき、次の問いに答えよ。
ただし円周率は\(\pi \)とする。
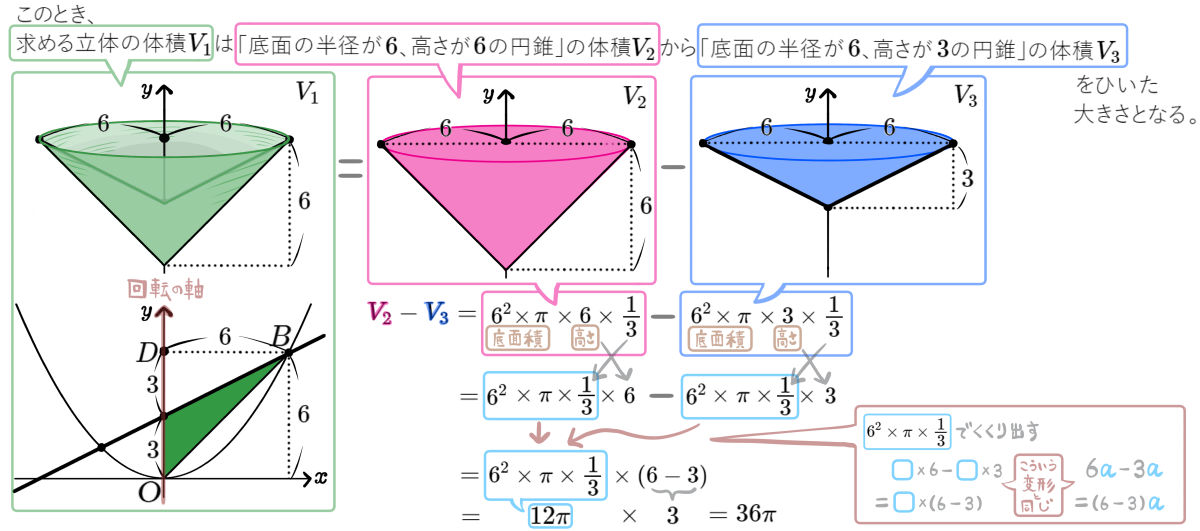
(1)△BCOを \(y\)軸を軸として一回転させてできる立体の体積を求めよ。

 つぎに線分DCと線分BDの長さを求めます。
つぎに線分DCと線分BDの長さを求めます。

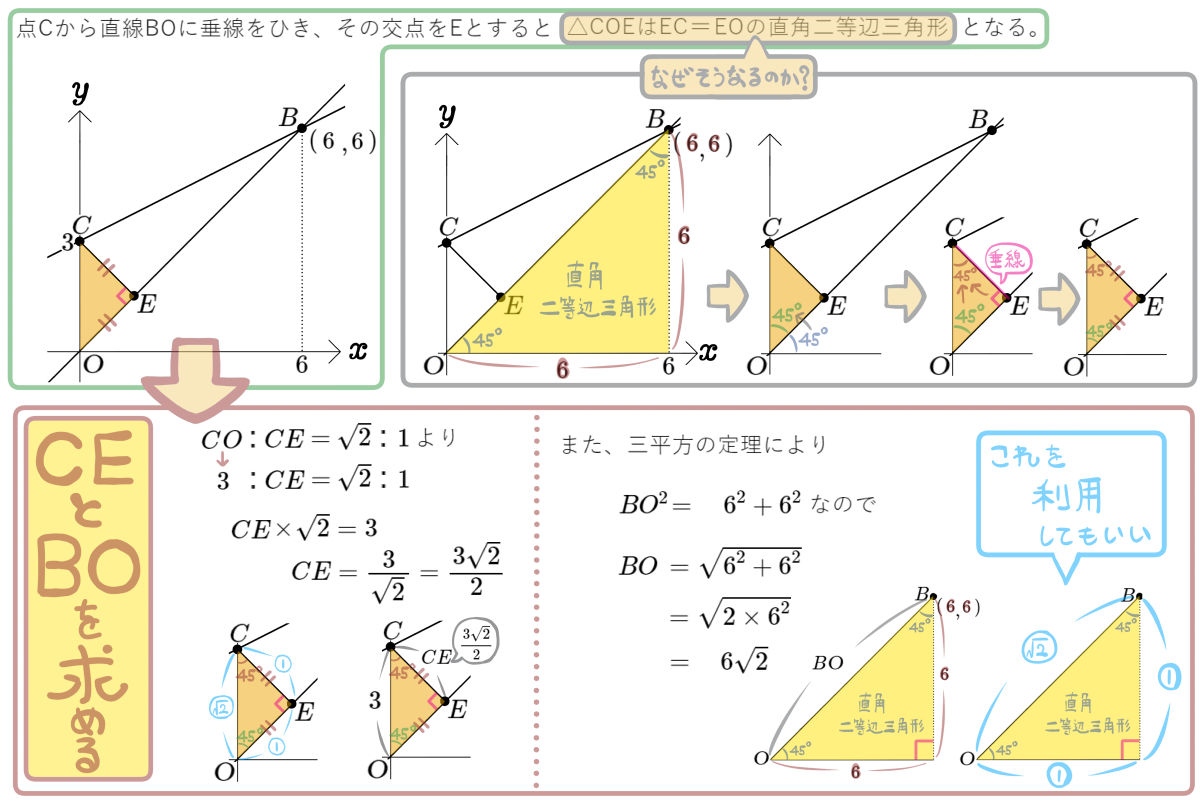
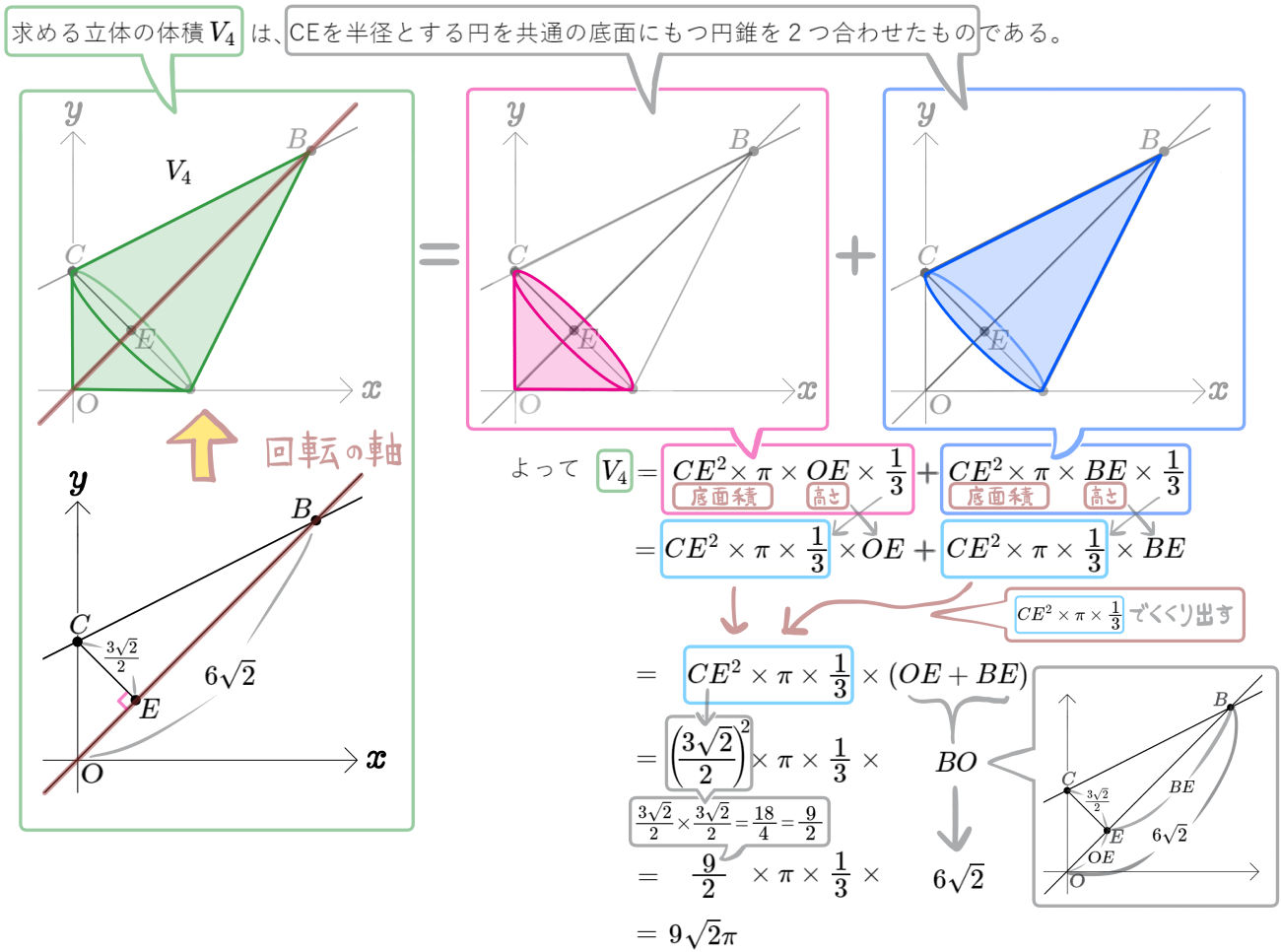
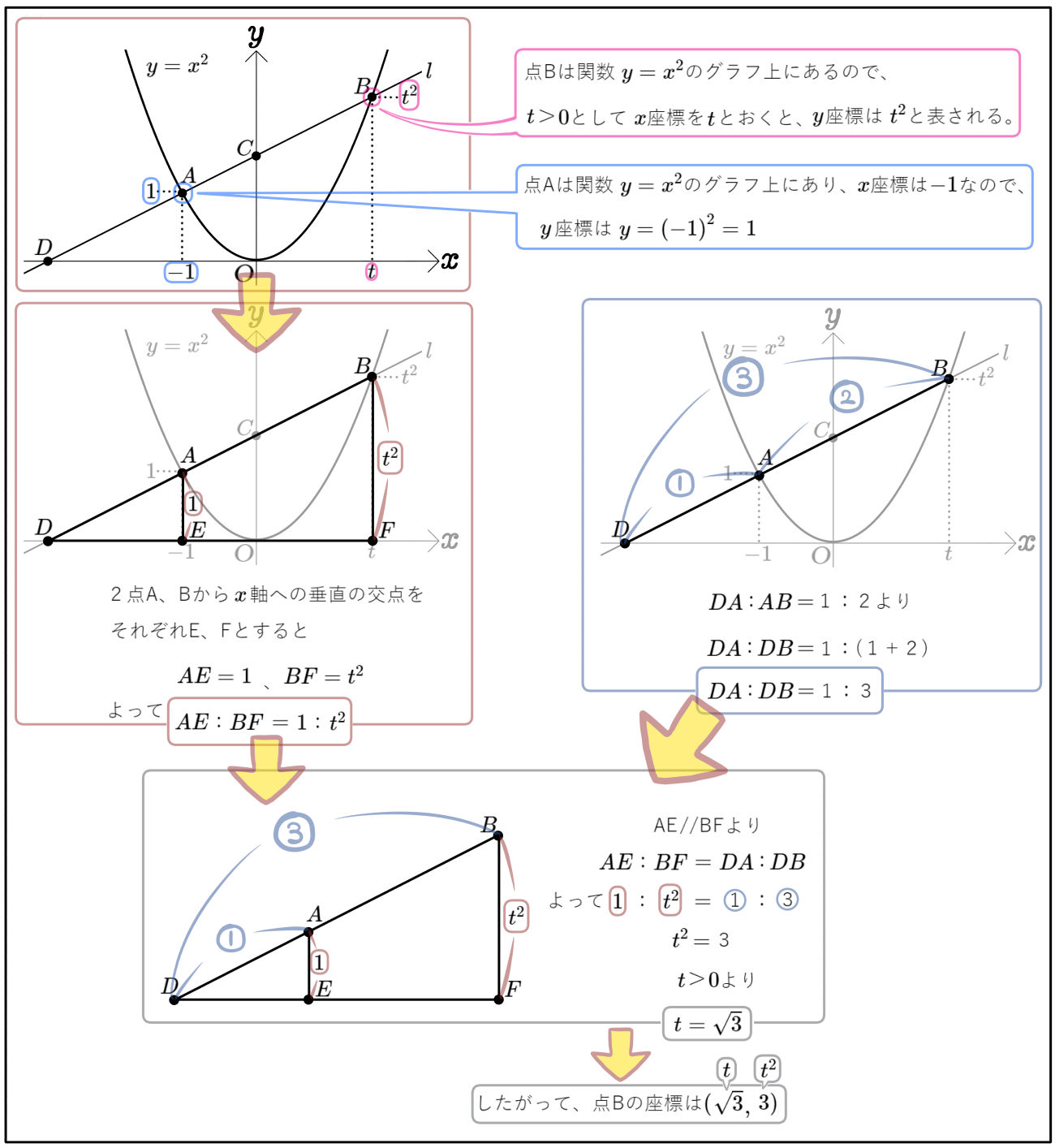
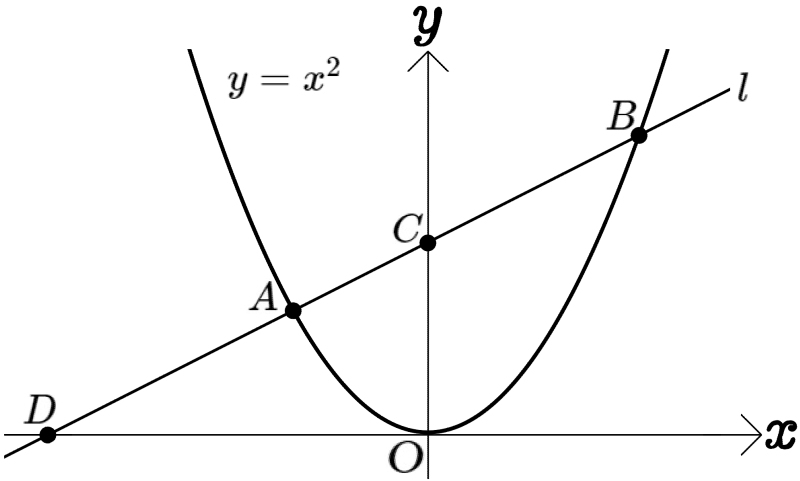 図のように、関数 \(y=x^{2}\)のグラフと直線 \(l\)が2点A、Bで交わっており、\(x\)座標が負であるほうをAとする。
図のように、関数 \(y=x^{2}\)のグラフと直線 \(l\)が2点A、Bで交わっており、\(x\)座標が負であるほうをAとする。
直線 \(l\)と\(x\)軸との交点をD、\(y\)軸との交点をCとするとき、次の問いに答えよ。
(1)点Aの \(x\)座標が \(-1\)、DA:AB=1:2のとき、点Bの座標を求めよ。
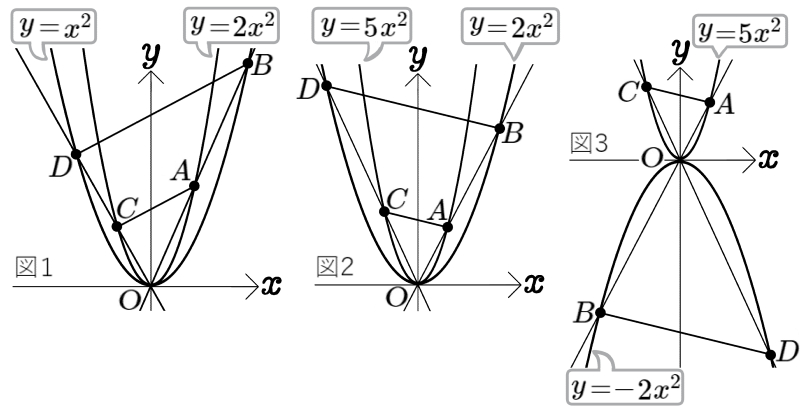
次の問いに答えよ。
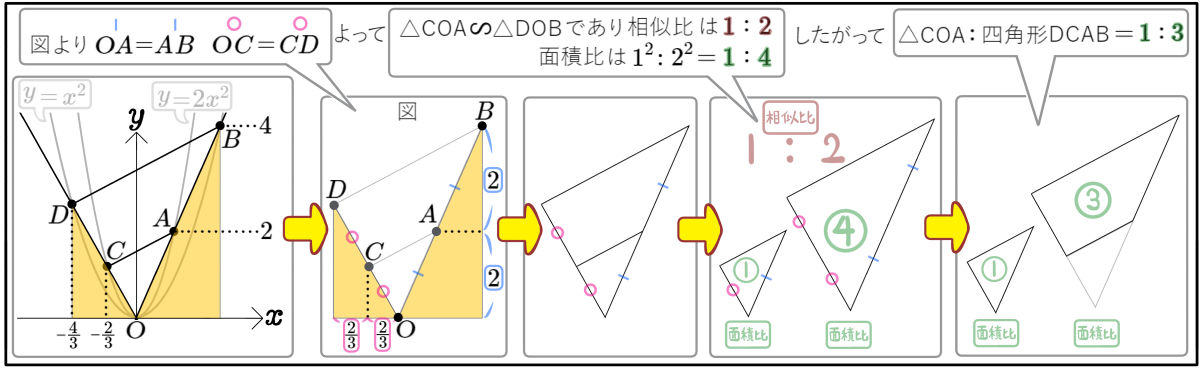
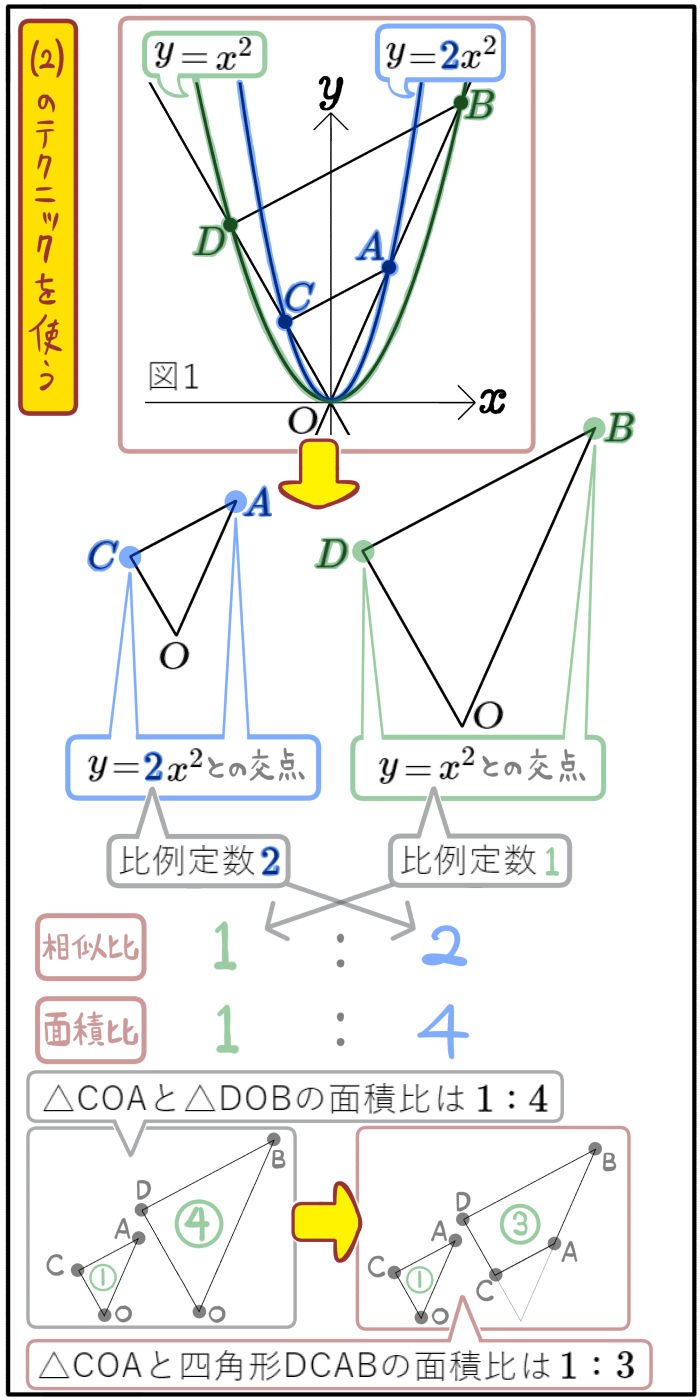
(1)図1のように、放物線 \(y=2x^{2}\)のグラフ上に2点A、Cがあり、放物線 \(y=x^{2}\)のグラフ上に2点B、Dがある。
2点A、Bの \(y\)座標がそれぞれ2、4、2点C、Dの \(x\)座標がそれぞれ \(-\dfrac{2}{3}\)、\(-\dfrac{4}{3}\)のとき、△COAと四角形DCABの面積について、最も簡単な整数の比で表せ。
【復習用】2次関数の難問対策の土台:公式&テクニック集まとめ




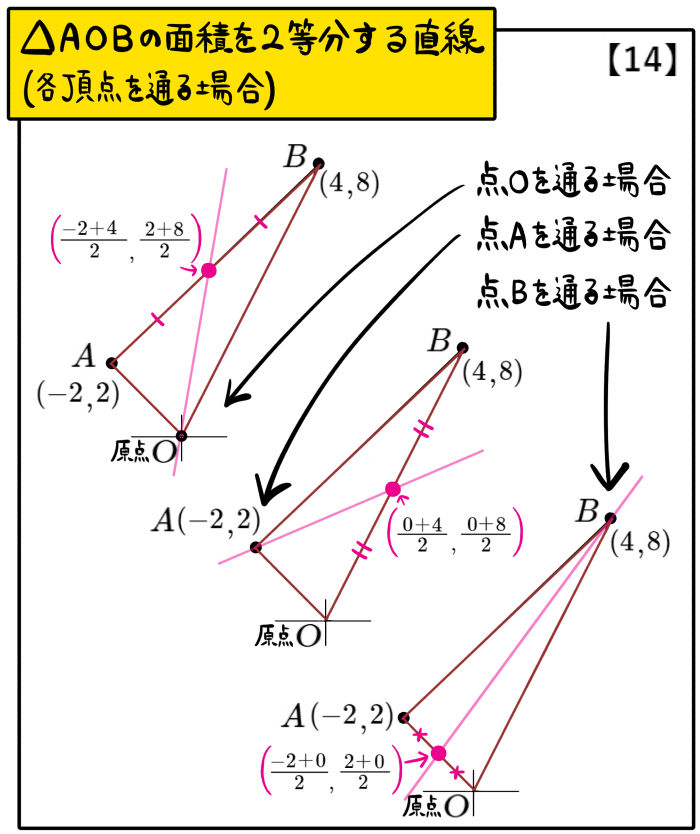
また、【16】は2等分ではありませんが、2つの三角形の面積比がテーマとなっています。












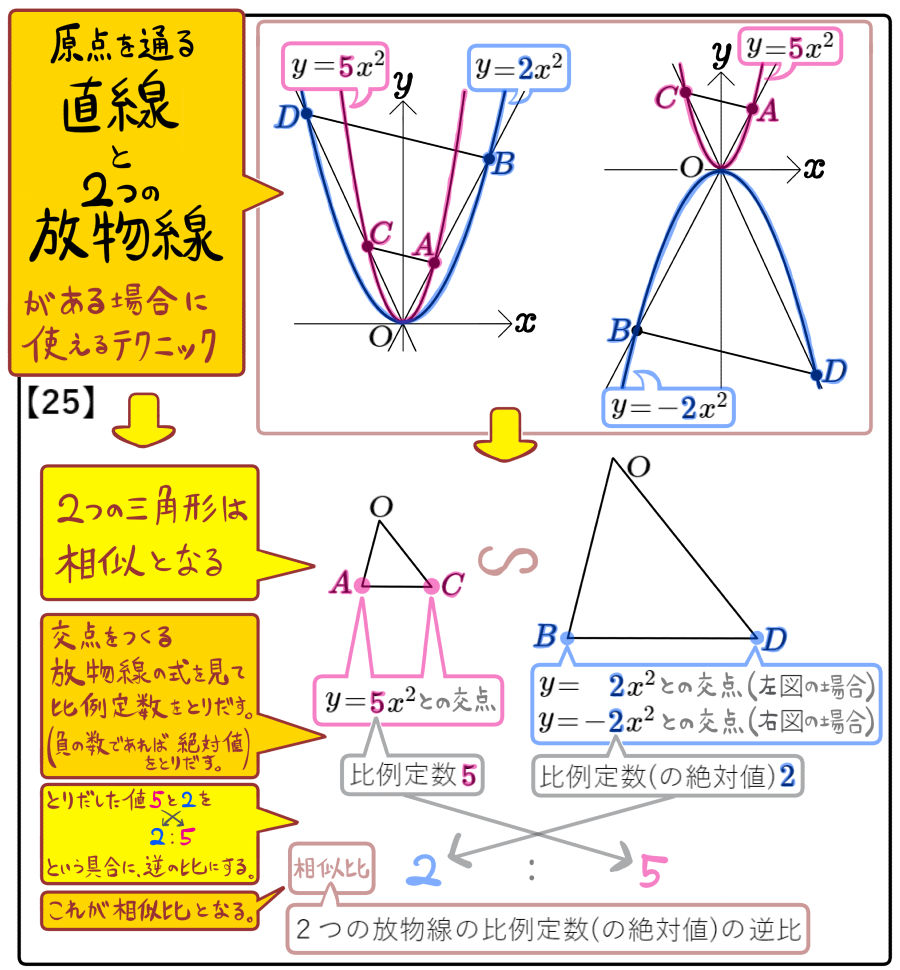
2次関数の応用・難問対策プリントの全内容




2:流れがわかりやすく、復習の時間を短縮してくれる。

その全ページがこちら↓です。