- 展開の応用問題(難問)同符号異符号に着目するパターン
- 様々なパターンの展開の難問
- 係数を求める展開の応用問題｜３項の式と３項の式の乗法
- 係数を求める展開の応用問題｜表にできないパターン
展開の応用問題(難問)同符号異符号に着目するパターン
(1) \(\left( 1+2a-3b\right) \left( 1-2a+3b\right) \) を展開せよ。
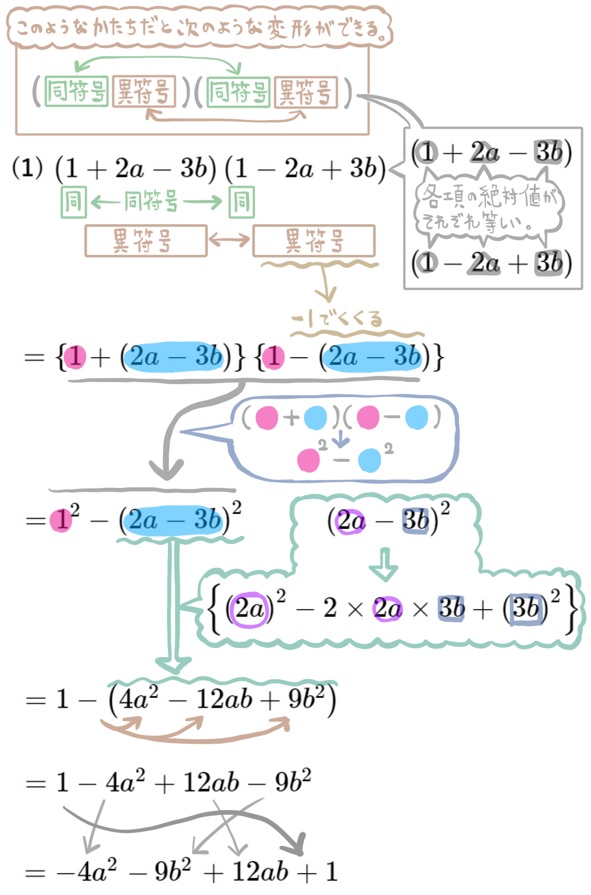
解説の部分にある通りのかたちにすることで (1)から(6)までは、同じような式変形が可能です。積となるそれぞれの式をチェックして、各項の絶対値の部分が同じであれば、このパターンかもと疑うとよいでしょう。←この説明の意味がわからなくても大丈夫です。とりあえず(1)から(6)までの解説の部分(特に同符号・異符号と書かれたあたりの式変形)をそれぞれ見比べてみてください。
(2) \(\left( 1-2a+3b\right) \left( 1+2a+3b\right) \)を展開せよ。
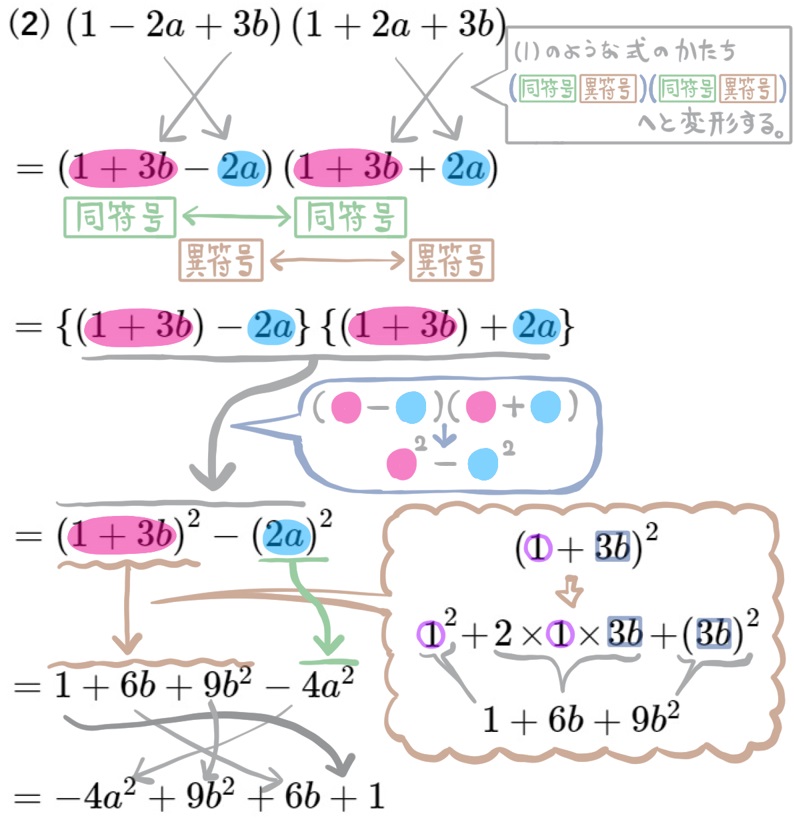
左の方にある\(1+3b\) の部分と、右の方にある\(1+3b\) の部分は、\(1\)も\(3b\)もそれぞれ同符号ですよね。それに対して、左の方にある\(-2a\) の部分と、右の方にある\(+2a\) の部分は、異符号になっています。
(同符号 異符号) (同符号 異符号)
と書いてあるのはそういう意味です。
そのような並びになるように、最初の変形をしています。
(3) \(\left( a-b+c-d\right) \left( a+b+c-d\right) \) を展開せよ。
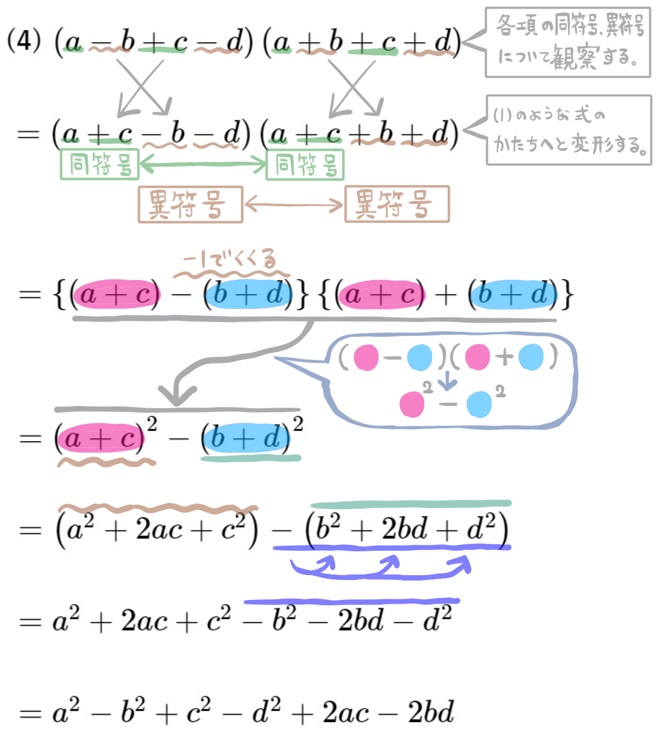
左の方にある\(-b\) の部分と、右の方にある\(+b\) の部分は、異符号になっています。それ以外の、\(a\) 、\(c\) 、\(-d\) の部分は左の方と右の方を見比べてみると、それぞれ同符号ですね。
(4) \(\left( a-b+c-d\right) \left( a+b+c+d\right) \) を展開せよ。
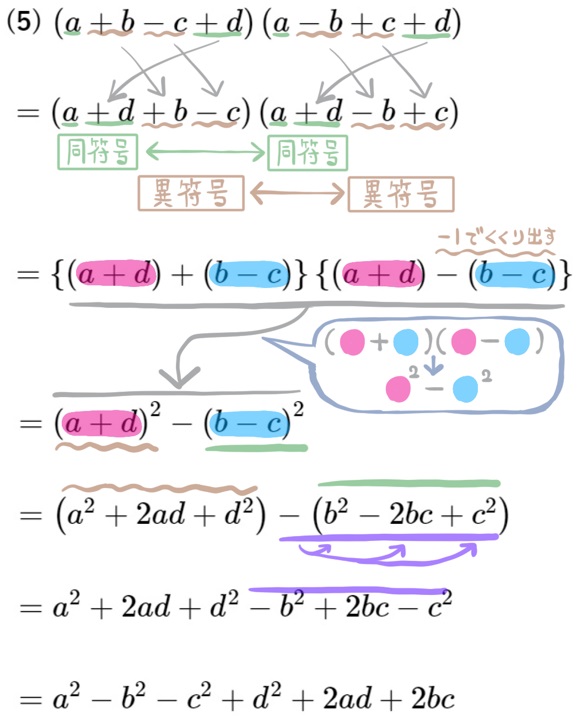
(5) \(\left( a+b-c+d\right) \left( a-b+c+d\right) \) を展開せよ。
(6) 次の式を簡単にせよ。
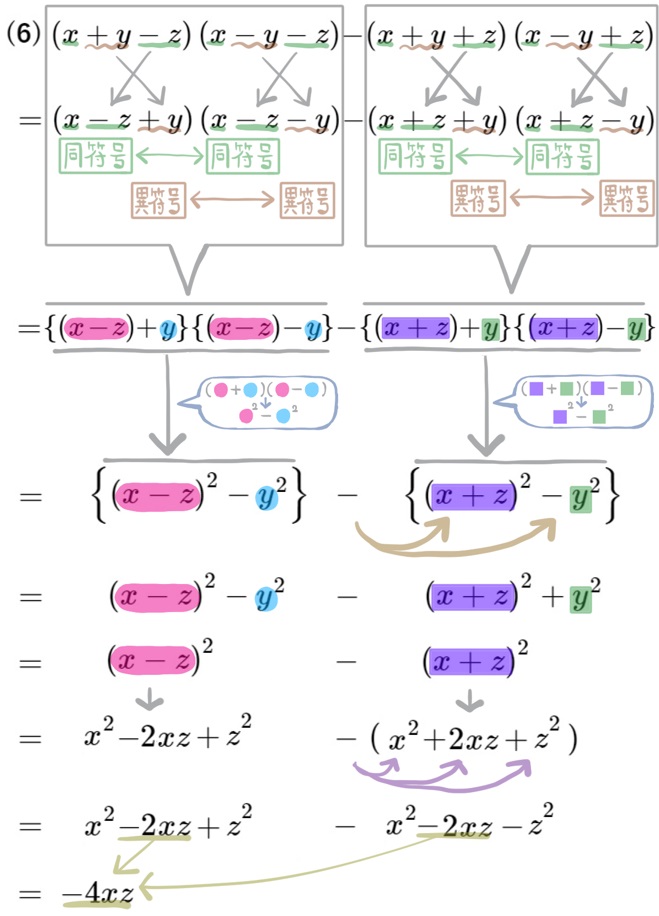
これまで(2)～(5)を解くときに最初に行っていた、「同符号異符号の組み合わせ探し」を左右の項で別々におこない、並び替える操作が必要になります。（言葉にするとややこしいですが、解説を見れば一目瞭然です）
様々なパターンの展開の難問
(7) \(\left( x-2\right) ^{2}\left( x+2\right) ^{2}\left( x^{2}+4\right) ^{2}\) を展開せよ。
最初の変形の際、指数法則でまとめるとその後が楽になります。
(8) \(\left( 3a+\dfrac{1}{3}b\right) ^{2}\left( 3a-\dfrac{1}{3}b\right) ^{2}\) を展開せよ。
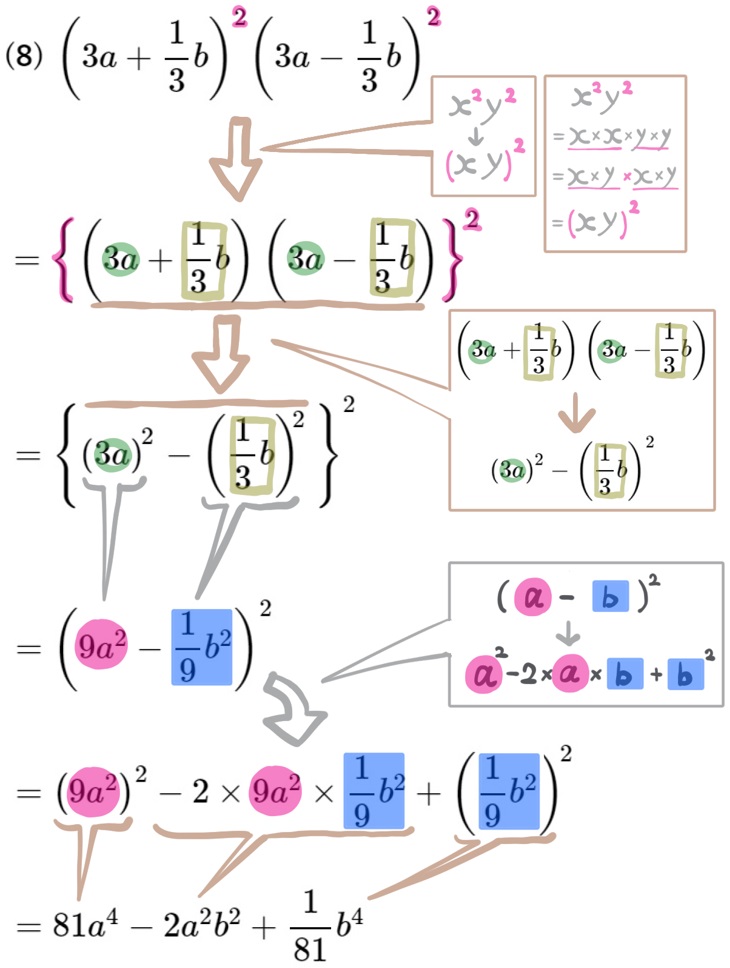
これも先程の問題と同じ要領で変形していきます。
(9) \({\small \left( -2x+3y\right) \left( -2x-3y\right) \left( -4x^{2}-9y^{2}\right)} \) を展開せよ。
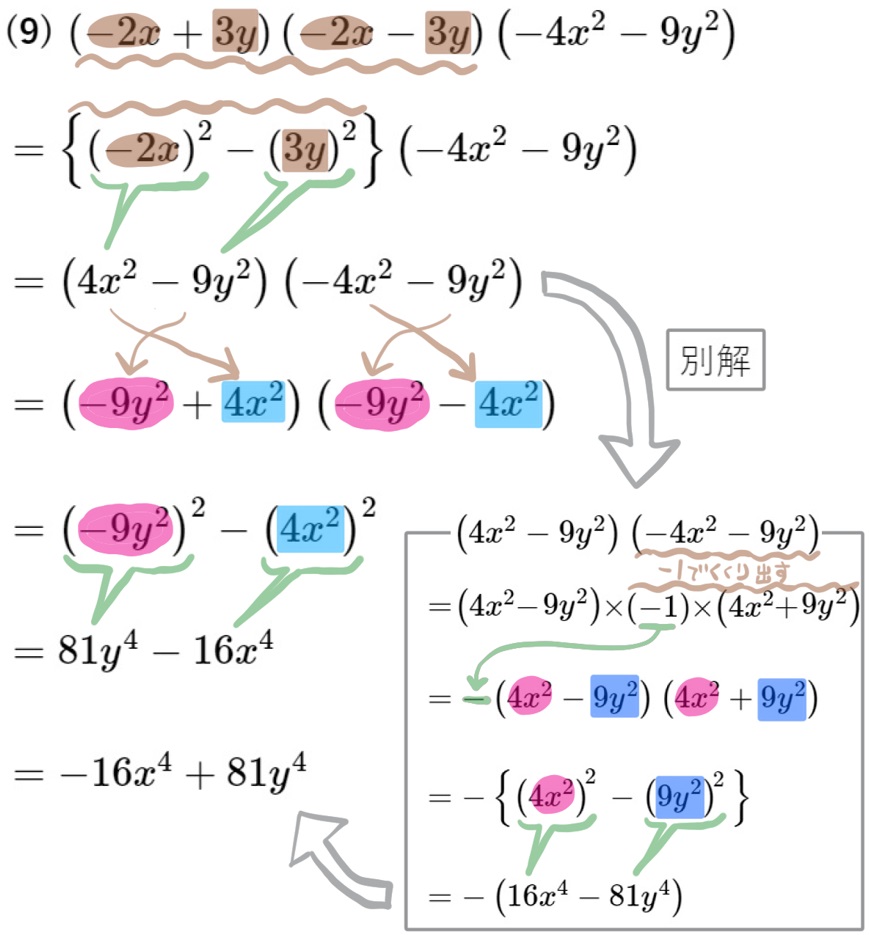
後半、指数の部分がややこしく見えるかもしれませんが、乗法公式による展開をそのまま使っています。
(10) \(\left( b+a\right) \left( a-b\right) \left( a-c\right) \left( c+a\right) \) を展開せよ。
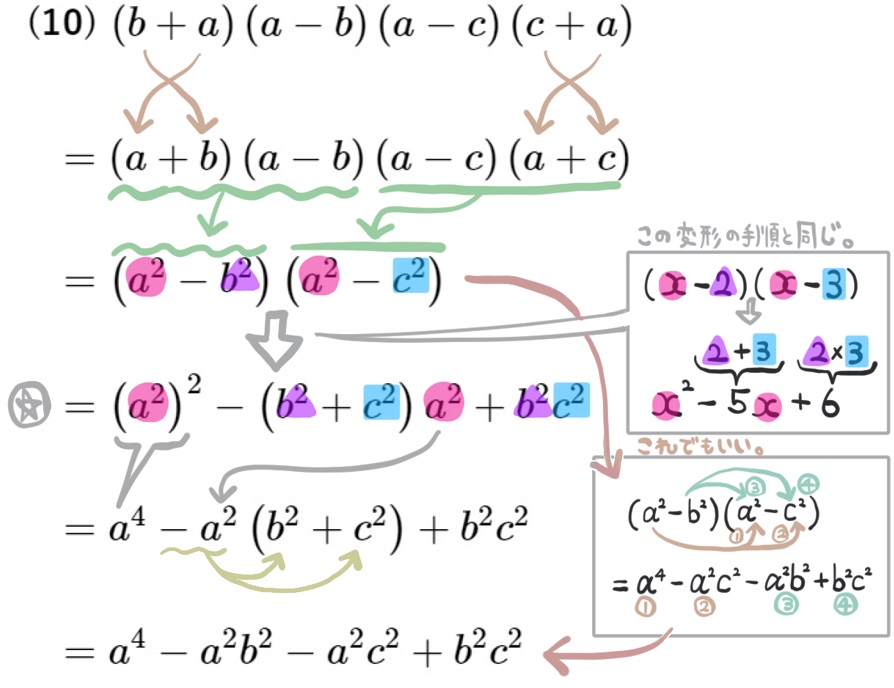
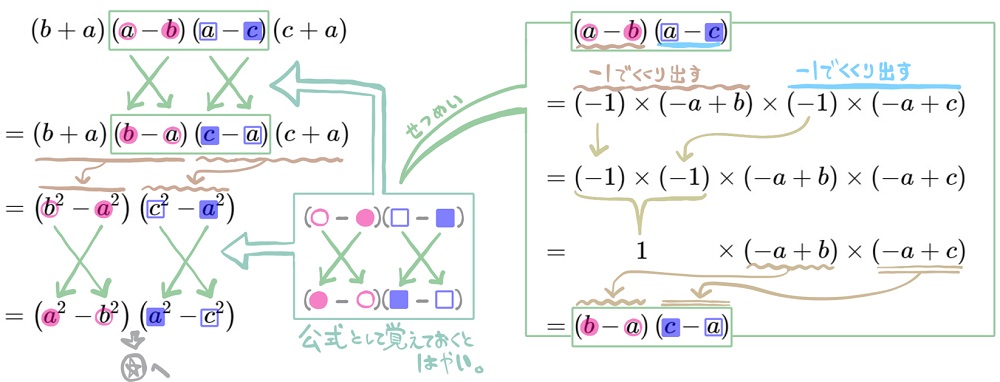「解説」の星マークのところに続きます。別解(おまけ)では、かなり回りくどい式変形をしていますが、問題によっては、知っていると便利な場合があります。難関私立を受験される中学生は知っておいても良いでしょう。
(11) \(a\left( b+c\right) \left( a-b-c\right) \) を展開せよ。
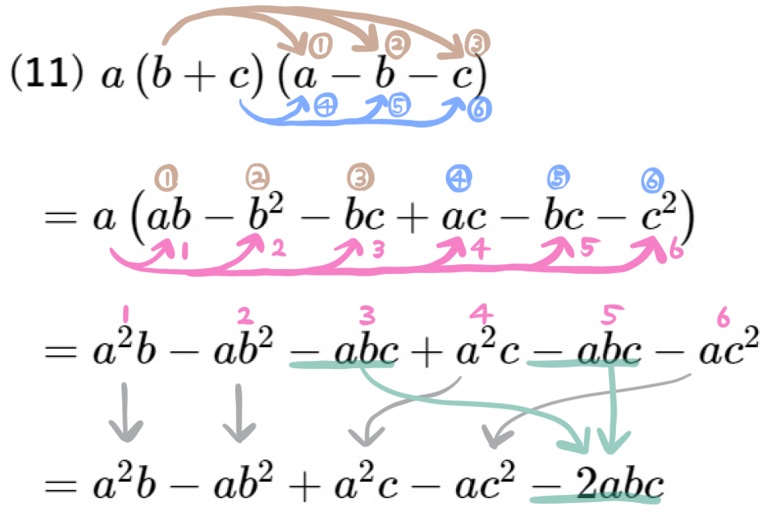
\(\left( b+c\right) \left( a-b-c\right) \)の部分がそこまで複雑な形ではないので、解説では、まずその部分だけ展開をしてから、それにaをかける方法をとっています。
別解では、\(b+c=X\) と置き換えられるよう変形しています。
(12) \(\left( b+3a\right) \left\{ \left( 3a\right) ^{2}+b^{2}\right\} \left( 6a-2b\right) \) を展開せよ。
\(6a-2b\) をとりあえず2でくくり出してみようとすることが重要です。その結果の式を眺めながら考えると、突破口を見つけ出しやすいです。
次の式を簡単にせよ。
(13) \({\small \left( -a-2b+3c\right) ^{2}-\left( a+2b\right) \left( a+2b-6c\right)} \)
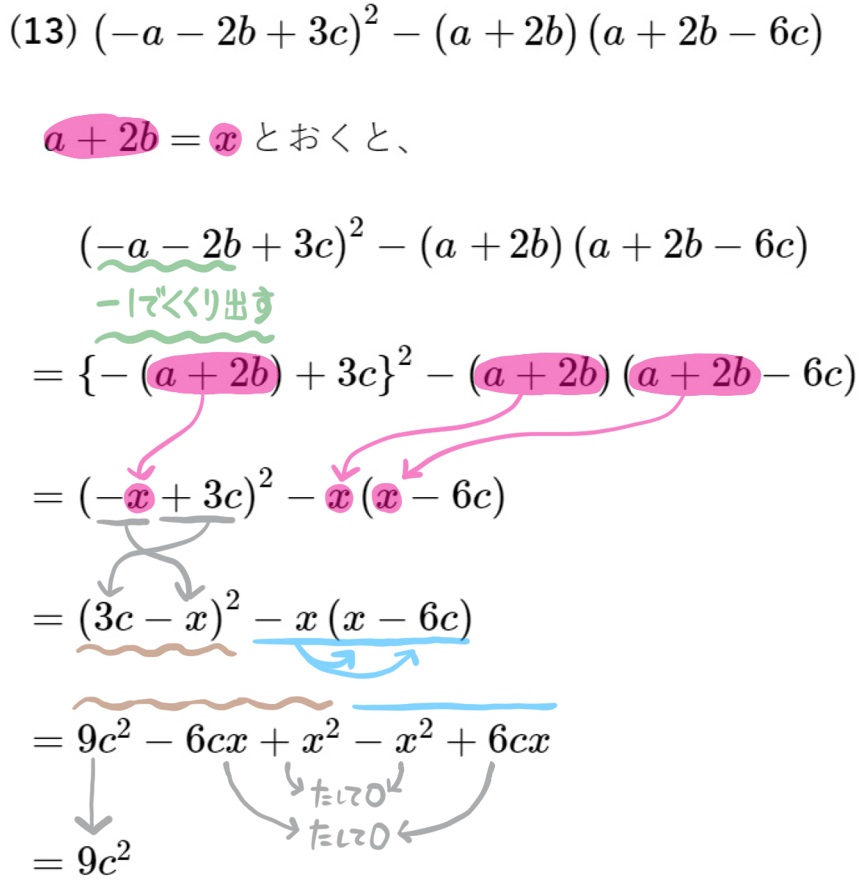
\(a+2b\) の部分が２カ所あるので、それに似た\(-a-2b\)の部分を変形し、\(a+2b\)を作り出せないかと発想します。もし\(a+2b\)を作り出せたなら、その部分をなにかしらの文字に置き換えてみよう、という次の手が浮かぶとさらに良いでしょう。
(14) \(-\left( 1+a^{2}b^{2}\right) \left( ab^{2}+b\right) \left( a-a^{2}b\right) \) を展開せよ。
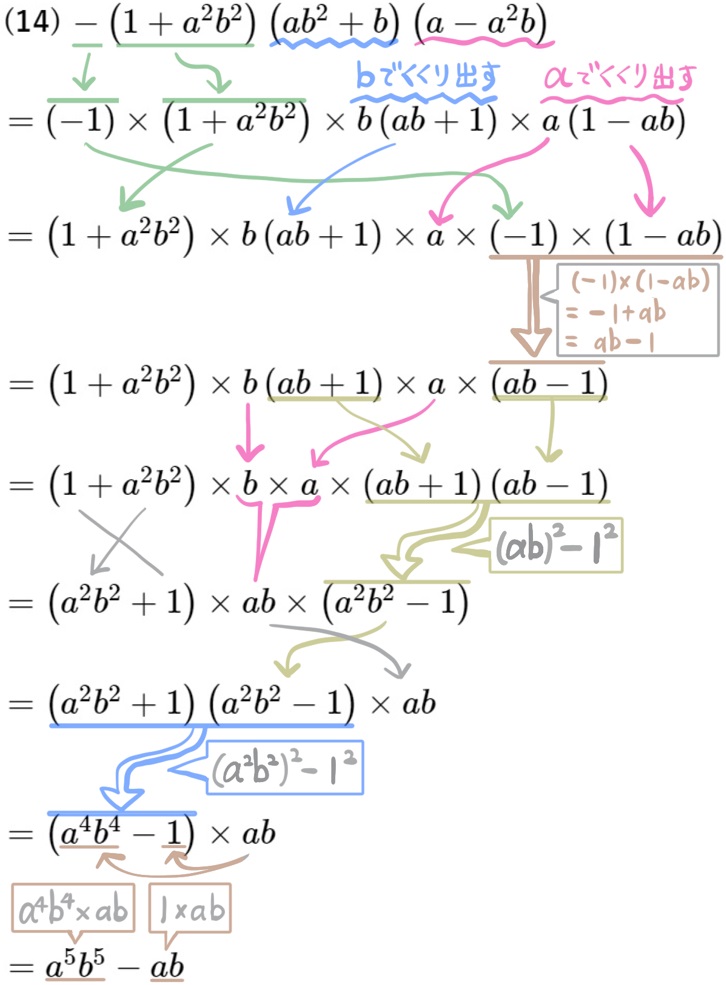
同じ形を作り出すために、最初の工程として、共通因数でくくり出すということをしています。難問です。
係数を求める展開の応用問題｜３項の式と３項の式の乗法
(15) \(\left( 3x^{2}+5x+1\right) \left( x^{2}+2x+2\right) \) を展開したときの \(x^{3}\) の係数を求めよ。
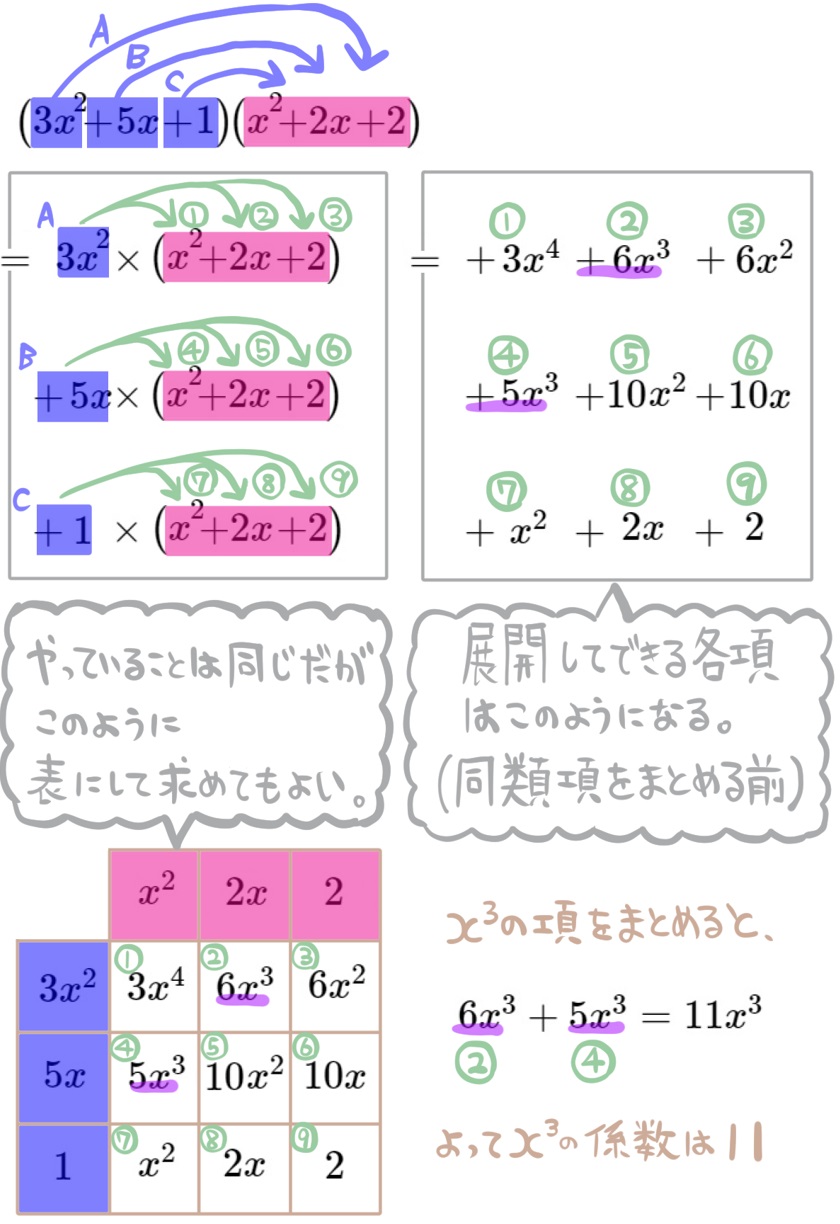
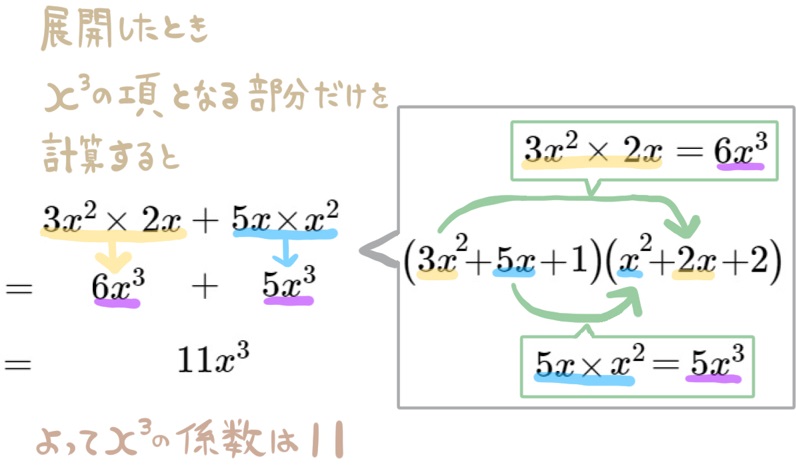
項が３つある多項式と多項式の乗法は、展開したときに９つの項が表れます。解法にあるように、表にして考えると整理しやすいです。
(16) \(\left( 3x^{2}+2x+1\right) \left( x^{2}-ax+2b\right) \) を展開すると \(3x^{4}+cx^{3}-12x^{2}-7x+d\) となる。
このとき \(c\) 、\(d\) の値をそれぞれ求めよ。ただし、\(a\) 、\(b\) 、\(c\) 、\(d\) は定数である。
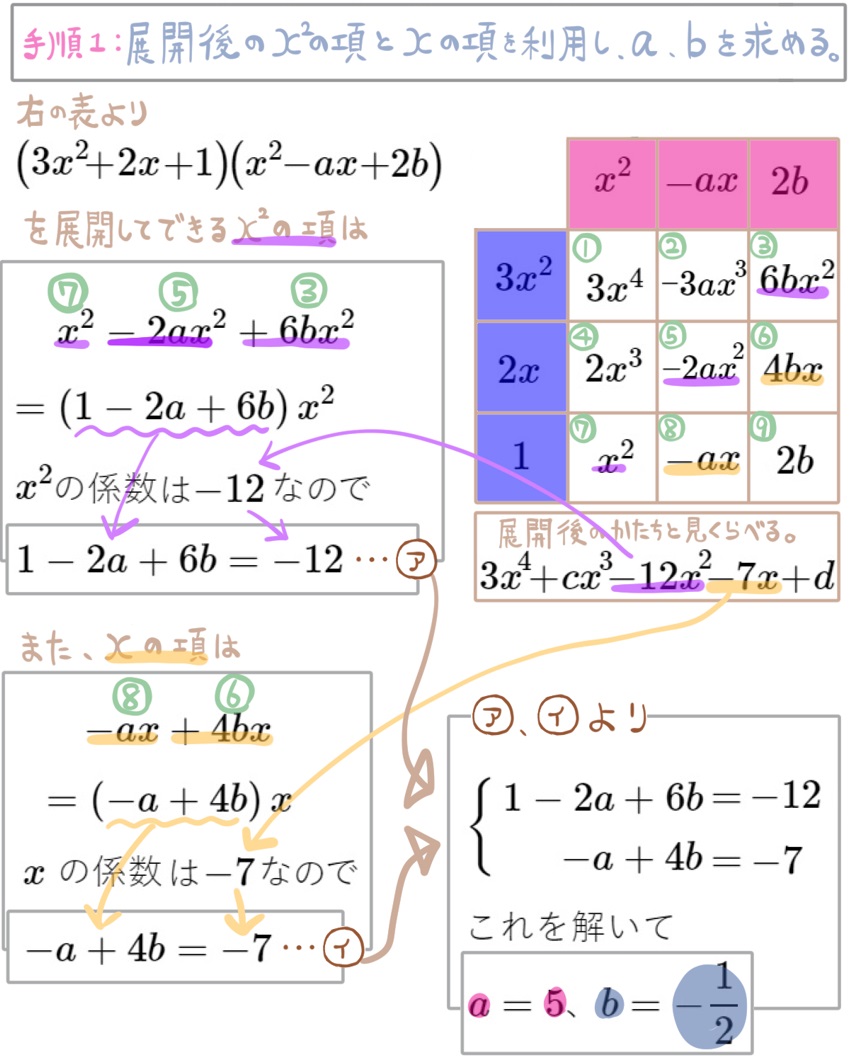
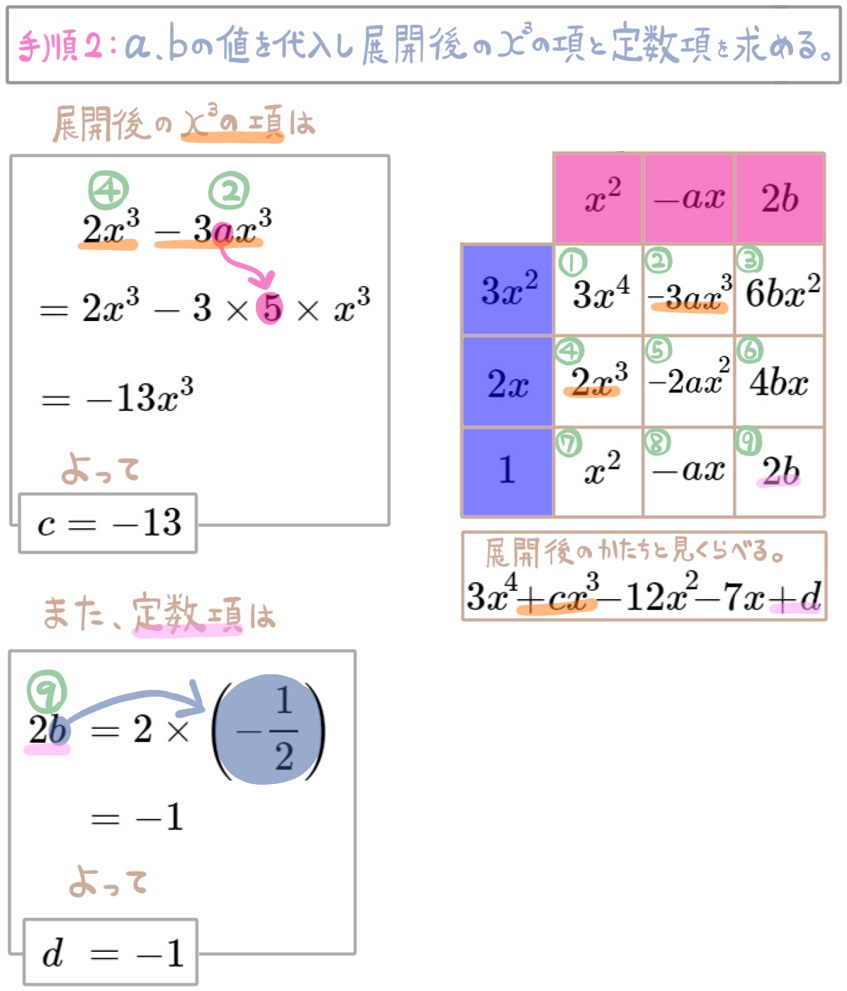
展開してできる項を把握しやすいよう、解説にあるように、表にして考えていきます。
係数を求める展開の応用問題｜表にできないパターン
(17) \(\left( 1+x\right) \left( 2+2x\right) \left( 3+3x\right) \) を展開したときの \(x\) の係数を求めよ。
（解説にある説明図を見てください。）
展開後にできる各項を求めるために「掛け合わされる３つの式の各項から、それぞれ項を１つずつ選んで掛け合わせてゆく」ということをします。
この方法により、展開後は全部で２×２×２=８つの項ができるということがわかります。(ただし同類項を整理する前の項の数としてですが)
ただしこの問題の解説では③までの３通りしか計算していません。
なぜなら「掛け合わされる３つの式の各項から、それぞれ項を１つずつ選んで掛け合わせてゆく」ことで、\(x\)の項ができる部分だけを計算したかったからです。
次の(18)では、与えられた式は同じまま、「\(x^{2}\) の係数を求めよ」と、問いだけを変更しています。
その解説部分と見比べてみてください。同じく３通り計算していますが、書け合わせるために選んだ項が、この問題の場合と異なっています。
(18) \(\left( 1+x\right) \left( 2+2x\right) \left( 3+3x\right) \) を展開したときの \(x^{2}\) の係数を求めよ。
「それぞれの式から項を一つずつ選び、それらを掛け合わせた結果、\(x^{2}\)の項ができるようにする。」←これをしたいがために、①から③までの３通りの計算をしていると思って解説を見てください。
(19) \(\left( 1+x\right) \left( 2+2x\right) \left( 3+3x+3x^{2}\right) \) を展開したときの \(x^{2}\) の係数を求めよ。
「あれ？全部\(6x^{2}\)が登場していない？」と思って、その部分だけを覚えないでください。途中の計算部分の意味がわかりやすいように式を作った結果、たまたまそうなってしまいました。すみません。
次の問題はそのようにはなっておらず、かなり実践的です。
(20) \({\small \left( 1+x\right) \left( 1+x+x^{2}\right) \left( 1+2x+3x^{2}\right)} \) を展開したときの \(x^{2}\) の係数を求めよ。
それぞれの式から項を一つずつ選び、それらを掛け合わせた結果、\(x^{2}\)の項ができるようにする。①から⑤までの計算式はその視点で作られたものだということがわかれば、とりあえず理解はOKです。
次はそれをスラスラ再現する練習をして完成です。慣れるまでは、解説の図を見ながら何度も口頭で説明するのが効率的です。
※この内容は特典として追加しています。
