



割合について中学数学~高校入試の文章題|基本~標準レベル
仕入れ値が200円の商品Aと仕入れ値が300円の商品Bがある。
商品Bを商品Aより5個多く仕入れた。
商品Aには仕入れ値の40%の利益を見込んで定価を付け、商品Bには仕入れ値の2割の利益を見込んで定価を付けて販売した。
その結果、商品A、Bともに定価で完売し、全体の利益が2400円になった。
仕入れた商品AとBの個数をそれぞれ求めよ。
仕入れた商品Aの個数は15個
仕入れた商品Bの個数は20個
商品Aの個数をa、商品Bの個数をbとおいて考えます。

売り上げ-仕入れ総額=利益
なので、上のような方程式になります。
また、商品Bの仕入れた数bは商品Aの仕入れた数aよりも5個多いので
a+5=b
となります。
この二つを連立方程式で解いて
a=15
b=20となり
仕入れた商品Aの個数は15個
仕入れた商品Bの個数は20個
となります。
※中学数学の定期テスト(公立)では、少し難しい問題に部類する難易度かと思います。
正方形の土地の縦の長さを4m長くし、横の長さを25%短くしたところ、その土地の面積が240㎡になった。もとの土地の面積を求めなさい。



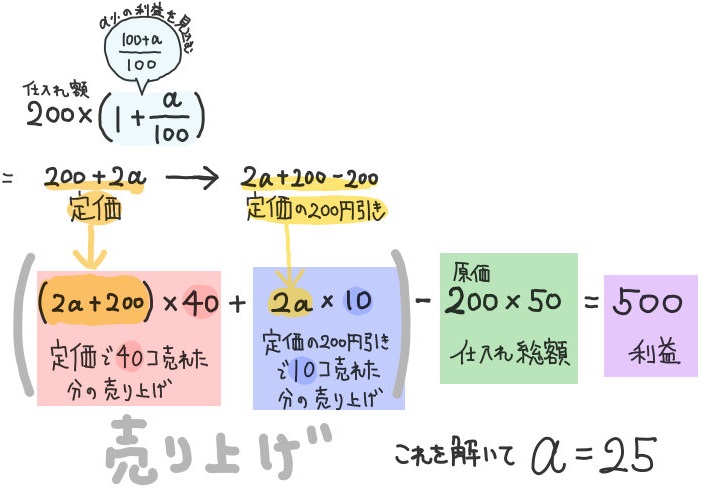
原価200円の品物を50個仕入れ、a%の利益を見込んで定価をつけて販売した。10個が売れ残ったので、定価の200円引きで販売したところ完売し、利益は500円であった。
aの値を求めよ。また、最初に見込んでいた利益を求めよ。


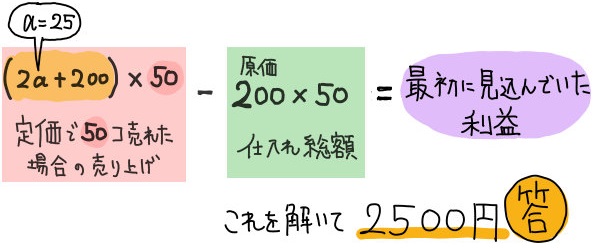
【最初に見込んでいた利益について】
aの値が25なので、25%の利益を見込んで定価を付けたことになります。
なので、仕入れ総額の10000円に対し25%の利益となります。
よって最初に見込んでいた利益は \(10000\times \dfrac{25}{100}=2500\)円となります。
売り上げ-仕入れ総額=利益
という公式を利用した場合は以下の計算になります。(別解)
 志望校にもよりますが、標準から難問の部類に入る練習問題です。
志望校にもよりますが、標準から難問の部類に入る練習問題です。
ある工場で、先月は製品Aと製品Bを合わせて49個つくった。今月は製品Aの数を先月の20%増やし、製品Bの数を25%減らしてつくったところ、製品Aと製品Bの総数は先月よりも1個減少した。
今月つくった製品Aと製品Bの数をそれぞれ求めよ。
今月つくった製品Aの数は30個
今月つくった製品Bの数は18個



xが15
yが24
だと判明しましたが、これは先月つくった製品Aと製品Bの数なので、答えではありません。
ここからさらに計算して今月つくった製品Aと製品Bの数を求めます。
今月つくった製品Aの数は \(25\times \dfrac{120}{100}=30\) 個
今月つくった製品Bの数は \(48-30=18\) 個
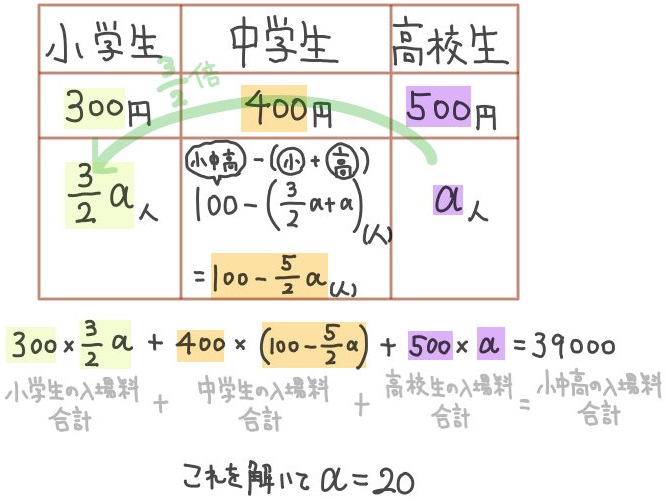
美術館への入場料が、小学生は一人300円、中学生は一人400円、高校生は一人500円である。
ある一日の入場者数は、小学生、中学生、高校生合わせて100人であり、それらの入場料の合計は39000円であった。
その一日の小学生の入場者数は高校生の入場者数の \(\dfrac{3}{2}\) 倍であった。
小学生、中学生、高校生それぞれの入場者数を求めよ。

小学生は小学生の入場者数は高校生の入場者数の \(\dfrac{3}{2}\) 倍なので、小学生の入場者数は\(\dfrac{3}{2}a\) とおけます。
また、その日の入場者数は、小学生、中学生、高校生合わせて100人だったので、中学生の入場者数は
100-(小学生の入場者数+高校生の入場者数)
となります。
そこから入場料についての方程式を完成させると次のようになります。
aの値が20ということは高校生の入場者数が20人であったということです。
その\(\dfrac{3}{2}\) 倍が小学生の入場者数なので、小学生の入場者数は30人ということになります。
小学生と高校生の入場者数の合計は50人ですので、残りの50人が中学生の入場者数になります。


割合について中学数学~高校入試の文章題|難問
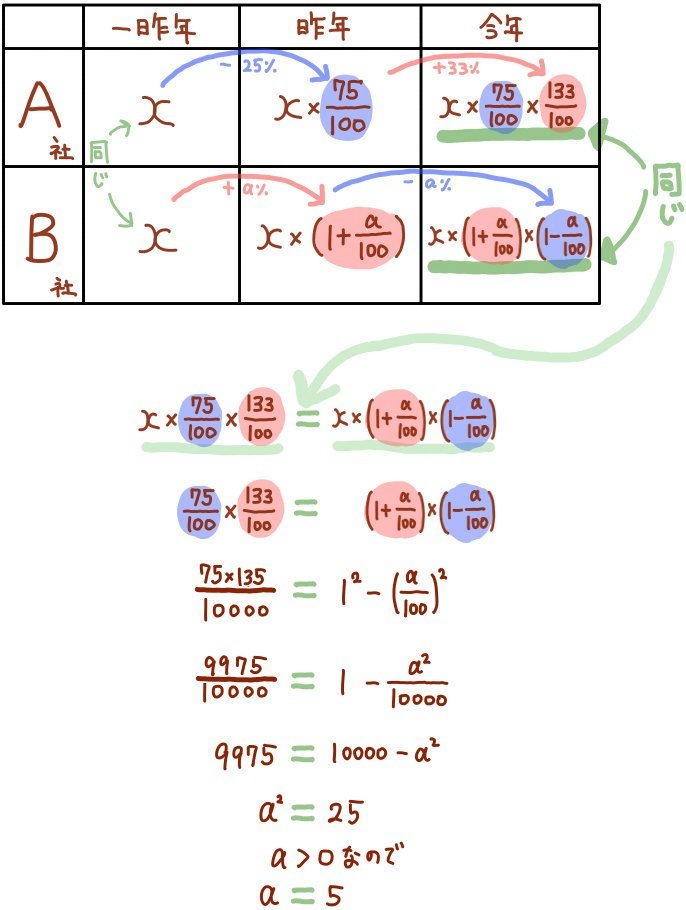
A社とB社は同じ商品を生産している。
A社の昨年の生産量は一昨年の生産量から25%減少し、今年の生産量は去年の生産量から33%増加した。
B社の昨年の生産量は一昨年の生産量からa%増加し、今年の生産量は去年の生産量からa%減少した。
両社の一昨年の生産量は等しい。
また、両社の今年の生産量も等しい。
aの値を求めよ。
ただし生産量は0ではなく、a>0とする。


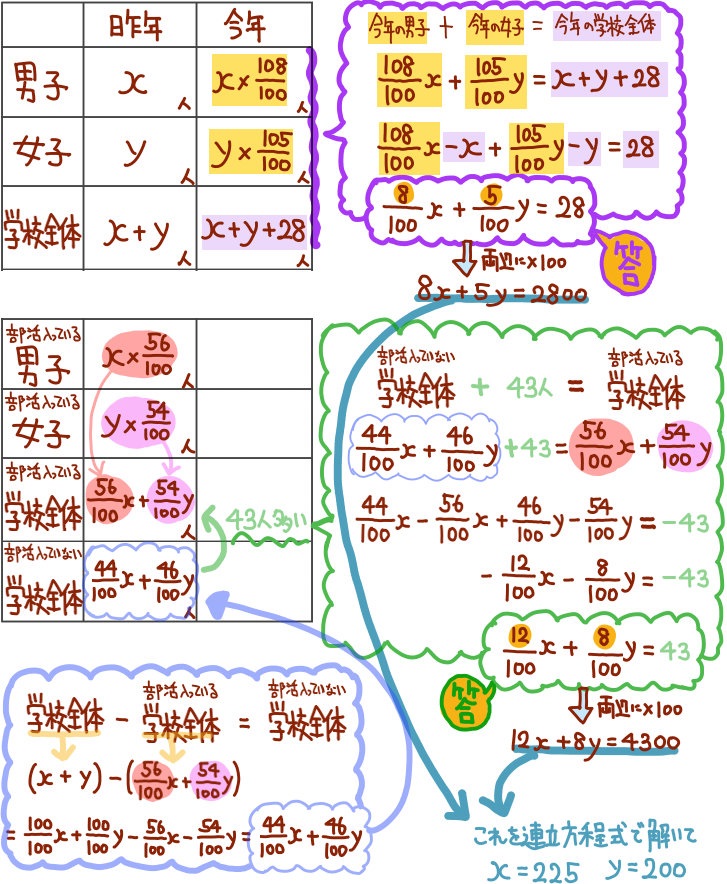
ある中学校では、今年度は昨年度に比べて男子が8%増え、女子が5%増えて学校全体で生徒数が28人増えた。
また、昨年度は男子の56%と女子の54%部活動に入っており、学校全体で部活動に入っている生徒の方が、部活動に入っていない生徒より43人多かった。
このとき、昨年度の男子生徒数をx人、昨年度の女子生徒数をy人として、人数についての連立方程式を作ると
\(\begin{cases}\dfrac{ア}{100}x+\dfrac{イ}{100}y=28\\
\dfrac{ウエ}{100}x+\dfrac{オ}{100}y=43\end{cases}\)
となる。
ア~オを求めよ。
また、今年度の男子生徒数と女子生徒数を求めよ。

その結果
アは8
イは5
ウエは12
エは8
となります。









































