







速さや道のりに関する連立方程式の文章題|基礎~標準
家から駅まで2800mの道のりをはじめは分速80mで歩き、途中から分速200mで走ったところ、家を出てから23分後に駅に着いた。
(1)歩いた道のりを\(x\)m、走った道のりを\(y\)mとして、\(x\)と\(y\)を求める連立方程式を作れ。


(2)歩いた時間を\(x\)分、走った時間を\(y\)分として、\(x\)と\(y\)を求める連立方程式を作れ。



池の周囲に道路がある。
AとBの2人が、この路上の同じ地点を同時に出発して、互いに反対方向に走ると、出発してから2分後に出会う。
同じ方向に走ると、AがBを1周引き離すのに出発してから16分かかる。
Bの速さを分速210mとする。
Aの速さと、池の周りの道路1周分の長さを求めよ。
 池を一周するタイプの、速さや道のりに関する文章題は、中学数学の定期テストで出題された場合、少し難しめの問題となります。
池を一周するタイプの、速さや道のりに関する文章題は、中学数学の定期テストで出題された場合、少し難しめの問題となります。
高校入試で見た場合、標準レベル~やや難問の類問題です。(もちろん志望校にもよりますが)
(立命館高校)
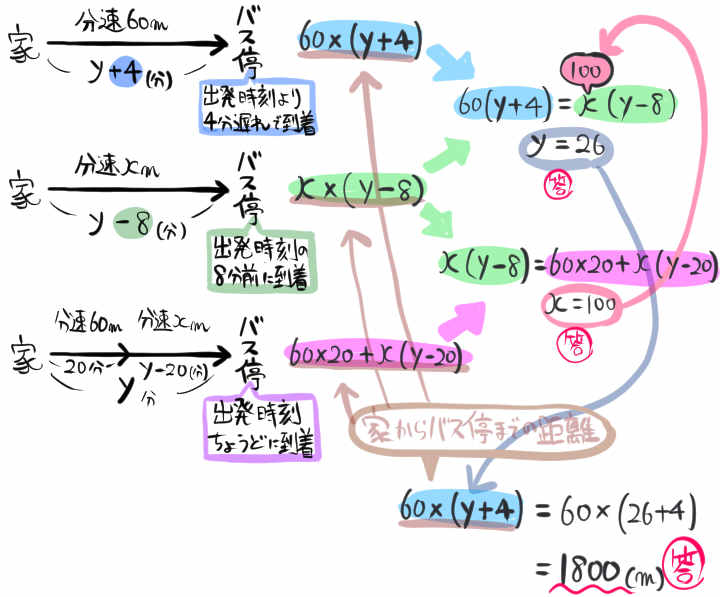
ある日、A君が家からバス停まで分速60mで歩いたところ、バスの出発時刻に4分遅れてバス停に着いた。
翌日、同じ時刻に家を出て分速xmで走ったところ、バスの出発時刻の8分前にバス停に着いた。
さらにその翌日、同じ時刻に家を出て分速60mで20分歩いてから分速xmで走ると、バスの出発時刻ちょうどにバス停に着いた。
A君が家を出てからy分後にバスが出発するとして、xとyの値を求めよ。
また、家からバス停までの距離も求めよ。
(愛光高校)
P地点とQ地点を行き来するための道として、Aコース、Bコースという2本の道がある。
ある時、太郎君と花子さんがP地点を同時刻に出発し、Q地点へ向かった。
太郎君はAコースを時速4㎞の速さで歩き、花子さんはBコースを時速5㎞の速さで歩いたところ、太郎君は花子さんより24分遅れてQ地点に到着した。
次に2人は同時にQ地点を出発してP地点へ向かった。
この時は花子さんはAコースを時速5㎞の速さで歩き、太郎君がBコースを時速4㎞の速さで歩いた。
すると、花子さんは太郎君より51分早くP地点に到着した。
Aコースの道のりを \(x\) ㎞、Bコースの道のりを \(y\) ㎞として、連立方程式をつくり、 \(x\) と\(y\) を求めよ。
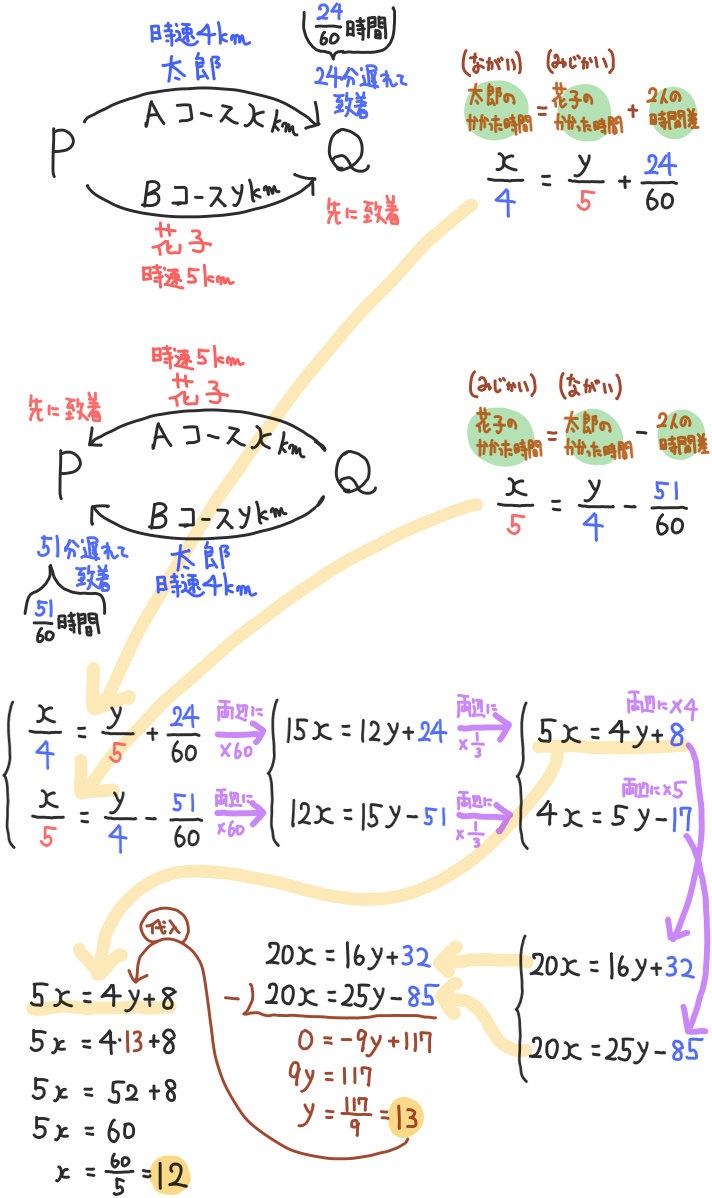

~~P地点からQ地点へ向かう場合~~
太郎君のほうが24分遅れて到着したので、花子さんよりも、太郎君が到着するまでの時間のほうが長かったことになります。
その時間差は24分なので
太郎のかかった時間=花子のかかった時間+24
という方程式ができます。
~~Q地点からP地点へ向かう場合~~
今度も太郎君のほうが51分遅れて到着したので、花子さんよりも、太郎君が到着するまでの時間のほうが長かったということですね。
その時間差は51分なので
太郎のかかった時間=花子のかかった時間+51分
という方程式ができます。
ただし、解説図では
花子のかかった時間=太郎のかかった時間-51分
という式を採用しています。

(明訓高校)
20㎞離れているP地点とQ地点との間を往復した。
行きは、P地点から30分間歩いた後、27分間車に乗り、Q地点に到着した。
帰りは、Q地点から1時間歩いた後、車に乗って、P地点に到着した。
車に乗った時間の比は、行きと帰りとではそれぞれ9:8であった。
歩く速さ時速\(x\)㎞、車の速さ時速\(y\)㎞として、連立方程式をつくり、\(x\)と\(y\)の値をそれぞれ求めよ。
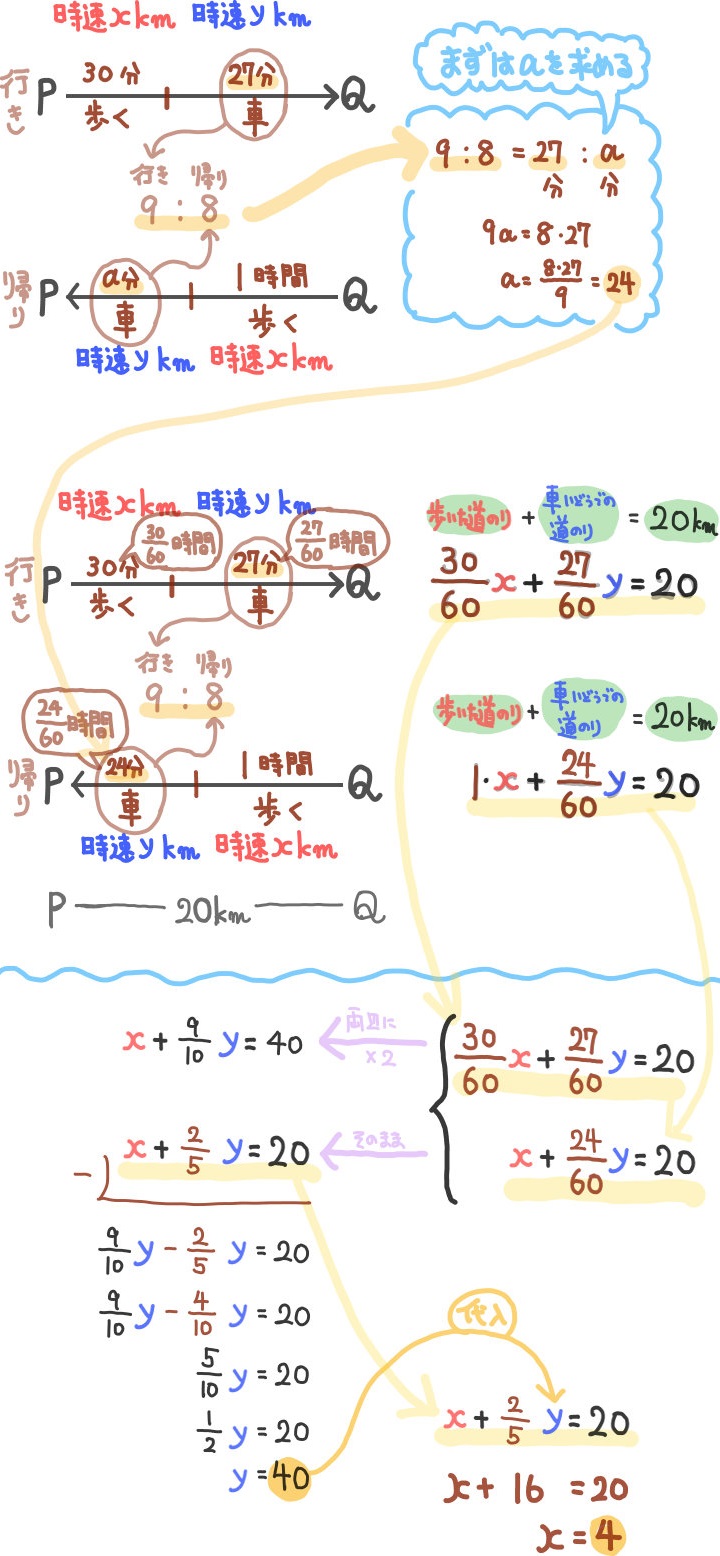

行きと帰りについて、速さや時間、道のりなどを書き込みます。
すると、帰りについての車での所要時間が不明であることがわかります。
それに対するヒントが、車での移動にかかった時間の比です。
行きと帰りとでは車での移動にかかった時間の比は9:8となっています。
それをもとに、まずは帰りの車移動にかかった時間を計算します。

次に、それぞれの時間の表記が『分』による表現となっています。
それに対して速さは時速での表記になっていますので、『分』を『時間』での表記に変えます。


あとは、行きと帰りについて、それぞれ、道のりについての方程式を作ります。
その連立方程式を解いて、xとyを求めて完了です。
(明訓高校)

速さや道のりに関する文章題の難問|中学数学~高校入試
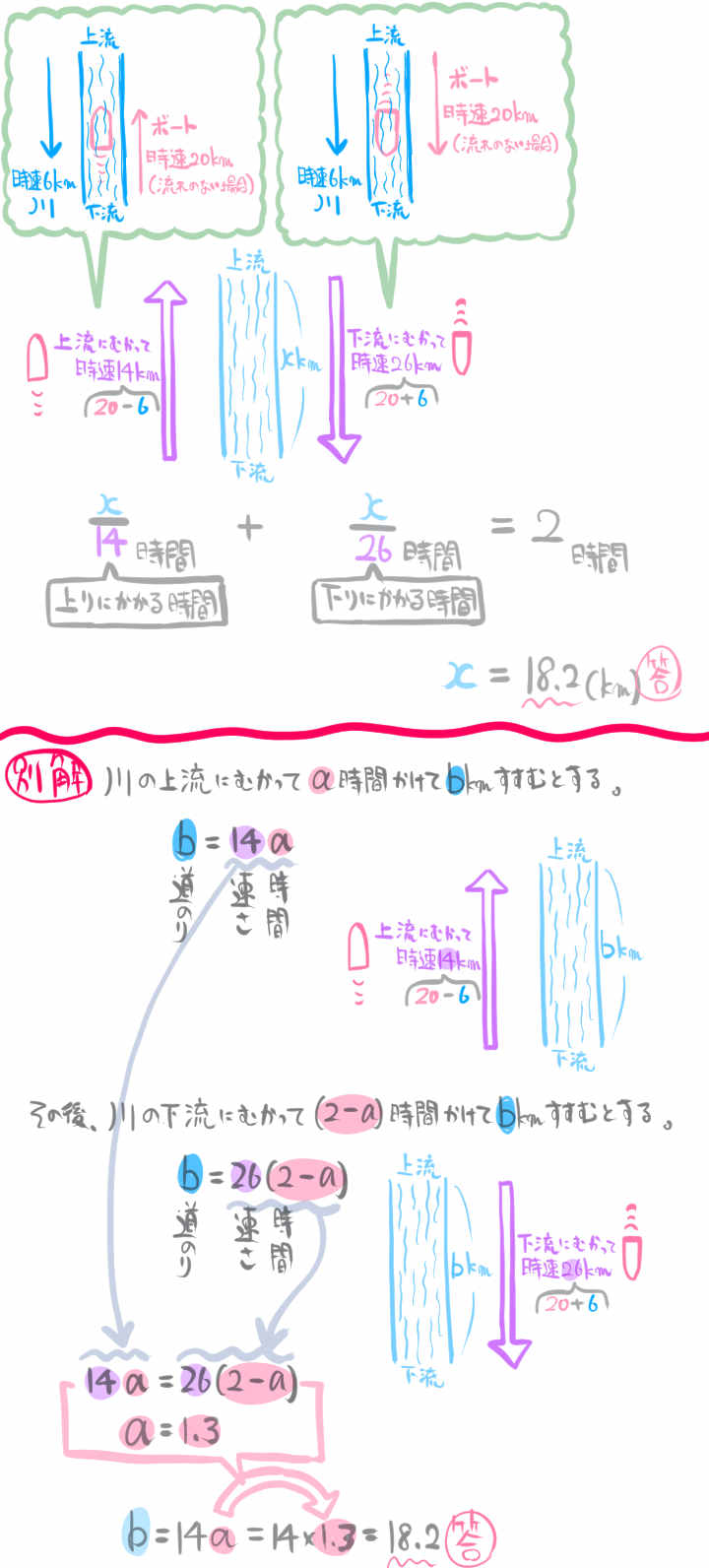
流れのない水面上を時速20㎞で走行できるボートがある。
今、このボートが時速6㎞の流れがある川の上流に向かって出発し、ある地点でエンジンをかけたまま引き返して2時間で出発地点に戻ってくる。
この場合、出発地点から何㎞の地点まで行くことができるかを求めなさい。
(立命館高校)
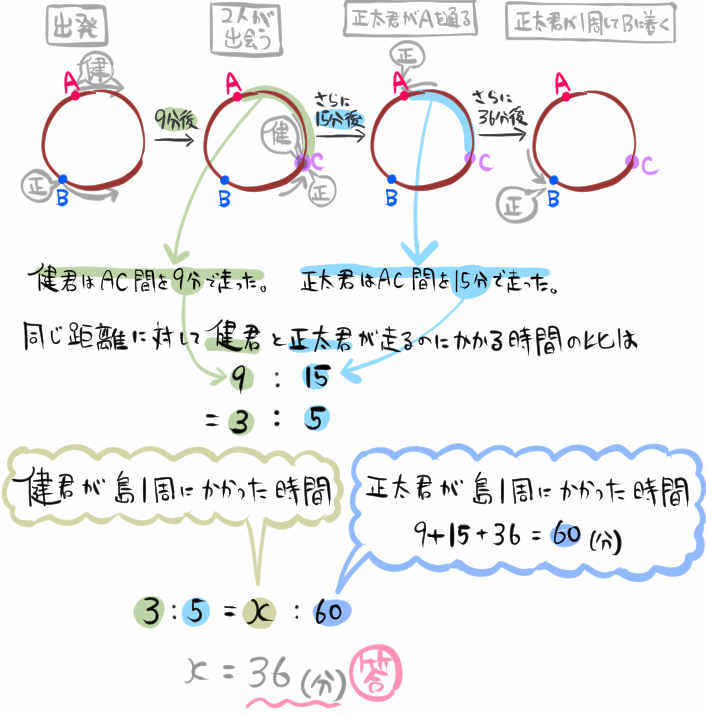
健君と正太君が、ある島を1周する道路をお互い逆向きに周回した。
健君は地点Aを右回りに、正太君は地点Bを左回りに同時に出発して一定の速さで走った。
出発してから9分後に2人は出会い、またその15分後に正太君は地点Aを通り、さらにその36分後に正太君は島をちょうど1周して地点Bに着いた。
このとき健君は島をちょうど1周するのに何分かかったのかを求めよ。
(西大和学園高校)
出発してから9分後に健君と正太君が出会った場所を地点Cとします。
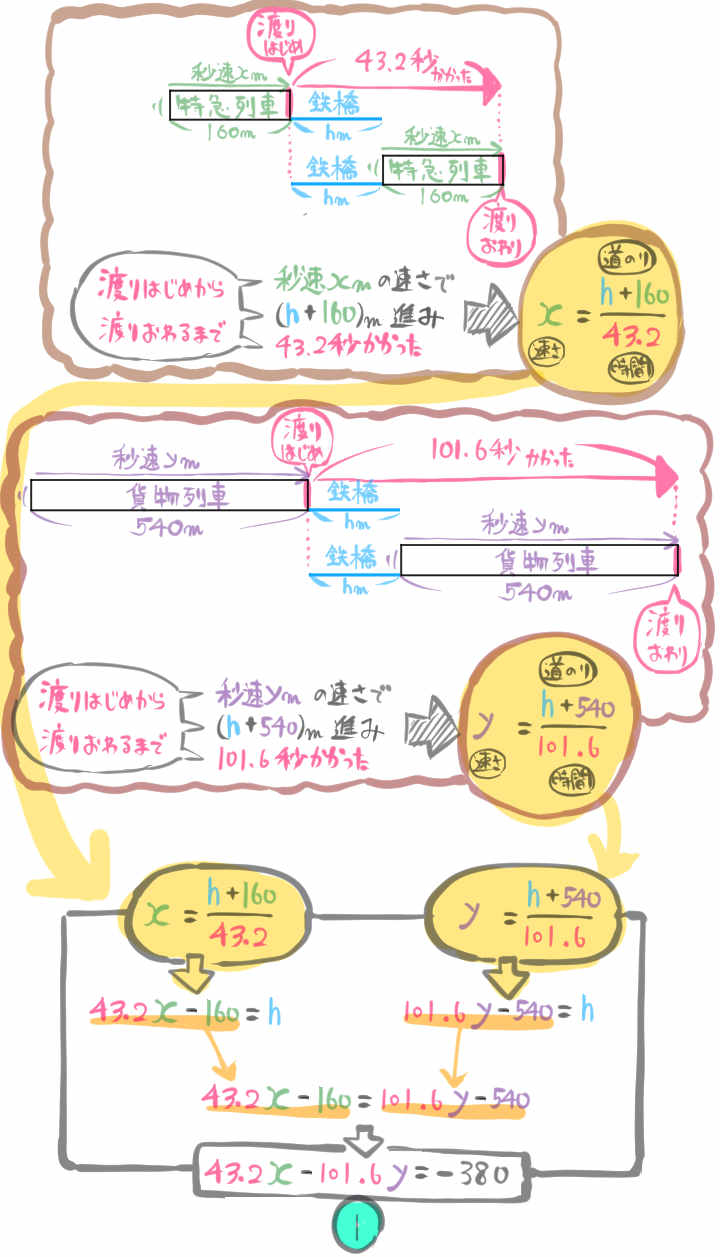
長さが160mの特急列車と、長さが540mの貨物列車がある。
1つの鉄橋を渡りきるのにかかる時間は
特急列車が43.2秒であり、貨物列車は101.6秒である。
また、この特急列車と貨物列車がすれ違うのに \(\dfrac{28}{3}\) 秒かかる。
この特急列車と貨物列車の速さはそれぞれ秒速何mか。
(ラ・サール高校)

『1つの鉄橋を渡りきるのにかかる時間は、特急列車が43.2秒であり、貨物列車は101.6秒である。』
という条件から、次の方程式を作ります。

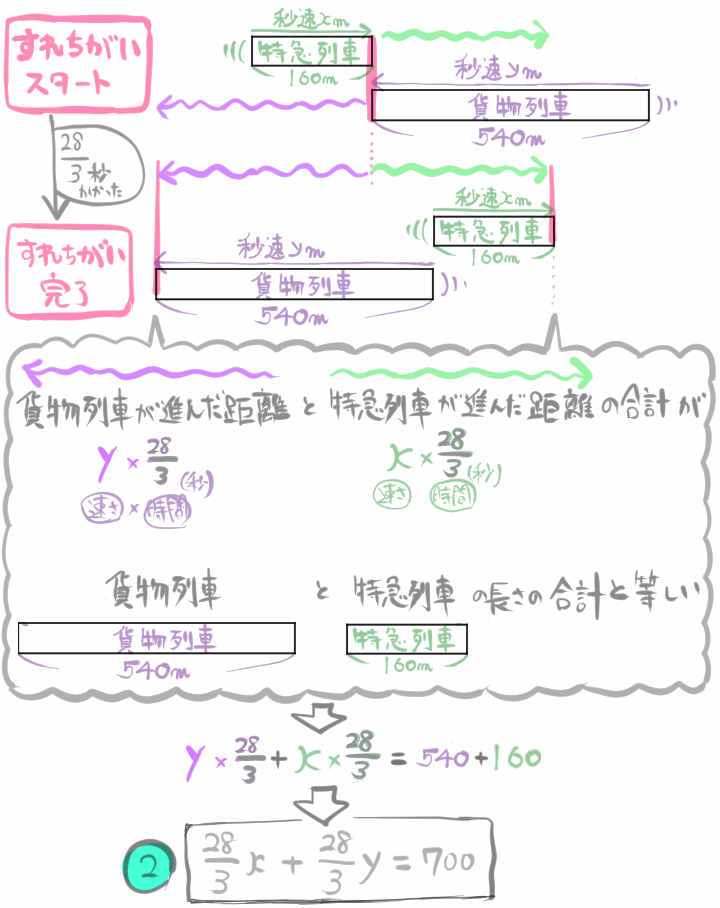

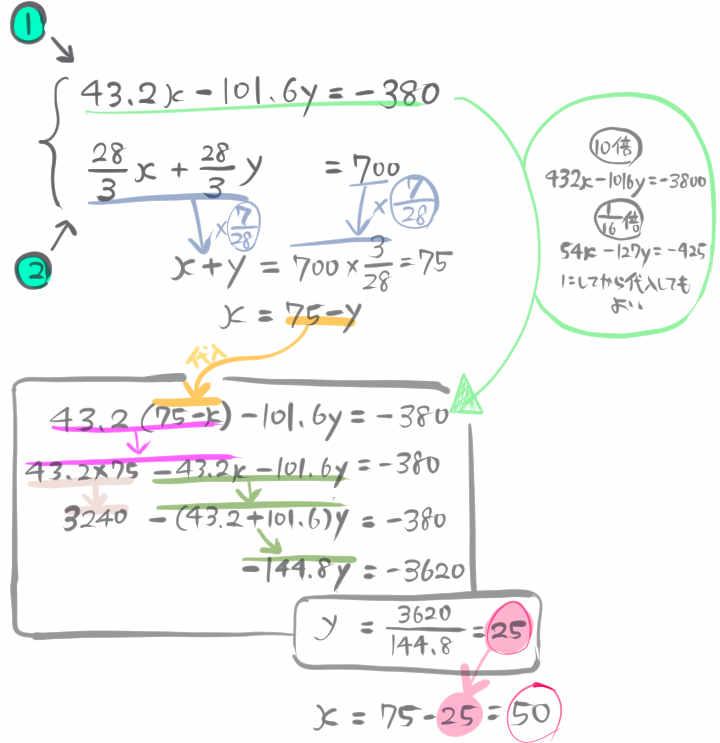
『列車が橋を渡る』という問題の場合、列車の長さと橋の長さを考慮する必要があります。また、『列車と列車がすれ違う』場合も、列車の長さを考慮しつつ、いかに方程式をつくればよいかを考える題材となっています。さいごの『連立方程式を計算する工程』は、なかなか歯ごたえがありますので、複雑な計算が苦手という方は、実際に手を動かして解いてみてください。
A地点からC地点の間に峠Bがある。
ある日、太郎君はA地点とC地点の間を往復した。
行きはA地点から峠Bまでx分かかって登り、峠BからC地点までy分かかって下り、その合計時間は32分であった。
帰りはC地点から峠Bまで登り、峠BからA地点まで下り、かかった時間は31分であった。
行きと帰りの登りの速さは等しく、行きと帰りの下りの速さも等しい。
登りの速さと下りの速さの比は3:4である。
xとyについての連立方程式を作り、xとyを求めよ。
また、A地点から峠Bまでの距離と、峠BからC地点までの距離の比を求めよ。
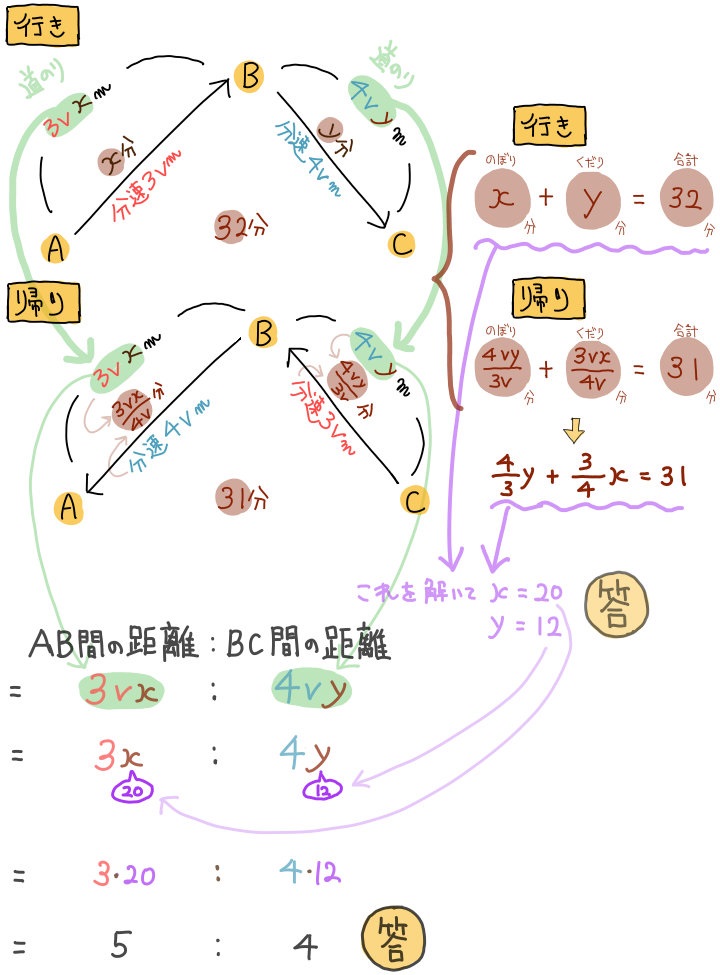
まず、行きの登りにかかった時間をx分とおき、下りにかかった時間をy分とおきます。
つまり行きにかかった時間の合計は32分なので
x+y=32
という式がつくれます。
また、登りの速さ:下りの速さ=3:4なので
登りの速さを分速\(3v\)m
下りの速さを分速\(4v\)m
とおきます。
これにより、AB間の道のりは3vxm、BC間の道のりは4vymと表現できます。
これをもとに、帰りの登り時間と下り時間を表現するとこうなります。
帰りの登り時間は \(\dfrac{4vy}{3v}\) 分
帰りの下り時間は \(\dfrac{3vx}{4v}\) 分
帰りの合計時間は31分なので
\(\dfrac{4vy}{3v}+\dfrac{3vx}{4v}=31\) となります。
約分をしてvを消去できるので
\(\dfrac{4}{3}y+\dfrac{3}{4}x=31\) となります。
これと、先程の
x+y=32
を連立方程式で解くと、xは20,yは12となります。

AからBの道のりは \(3vx\) mで、BからCの道のりは \(4vy\) mとなります。
ここのxとyに先程求めたものを代入すれば距離AB:BCの比が算出できます。
答えは5:4です。
公立中学の数学定期テストではなかなか出ないレベルの文章題です。
高校入試問題としては難問と言っていいでしょう。
ある公園の遊歩道のスタート地点に、太郎君と30人のグループがいる。
太郎君は分速60mの速さで歩く。
30人のグループは分速150mの速さで20m間隔で1人ずつ走り出す。
今、太郎君と30人のグループの先頭が同時に出発した。
スタート地点から100メートル離れた所にP地点がある。
太郎君がP地点を通過するまでに、30人のグループのうち何人がP地点を通過することができるか。(大濠高校)
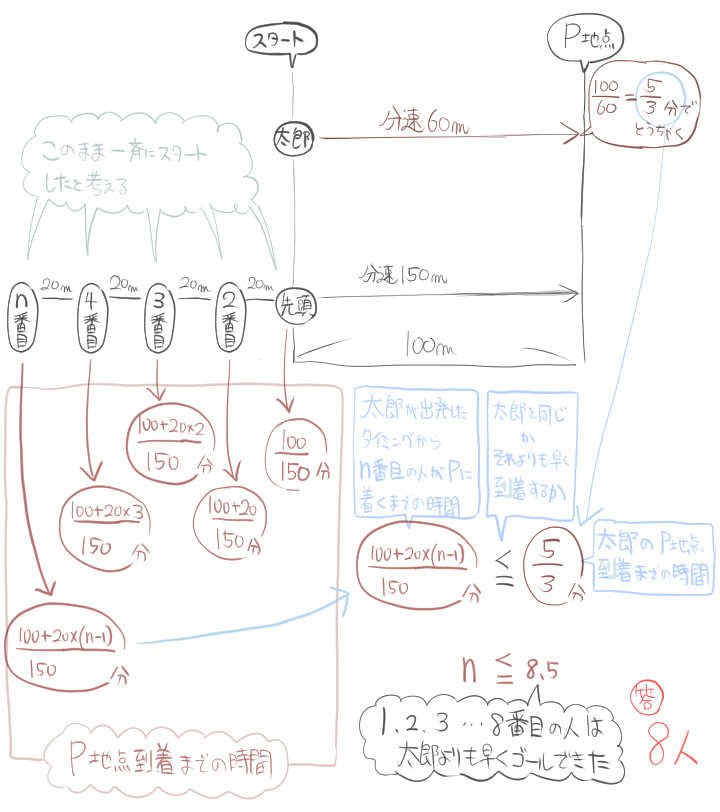
ここの解答方法では『30人のグループが20m間隔で最初からずらりと並んでいて全員が一斉にスタートした』として考えました。
3.2km離れた駅と学校の間を一定の速さで往復するバスがある。
ある生徒がこのバスと同時に駅を出発して分速80mの速さで歩いて学校へ向かった。
学校に到着するまでに2度バスとすれ違い、また1度だけバスに後ろから追い抜かれた(出発時は含めない)。
このとき、バスの速さを分速xmとしてxの範囲を求めよ。
ただしバスは学校と駅のどちらでもちょうど5分停車し、途中に停留所はないものとする。
(慶應義塾志木高校)
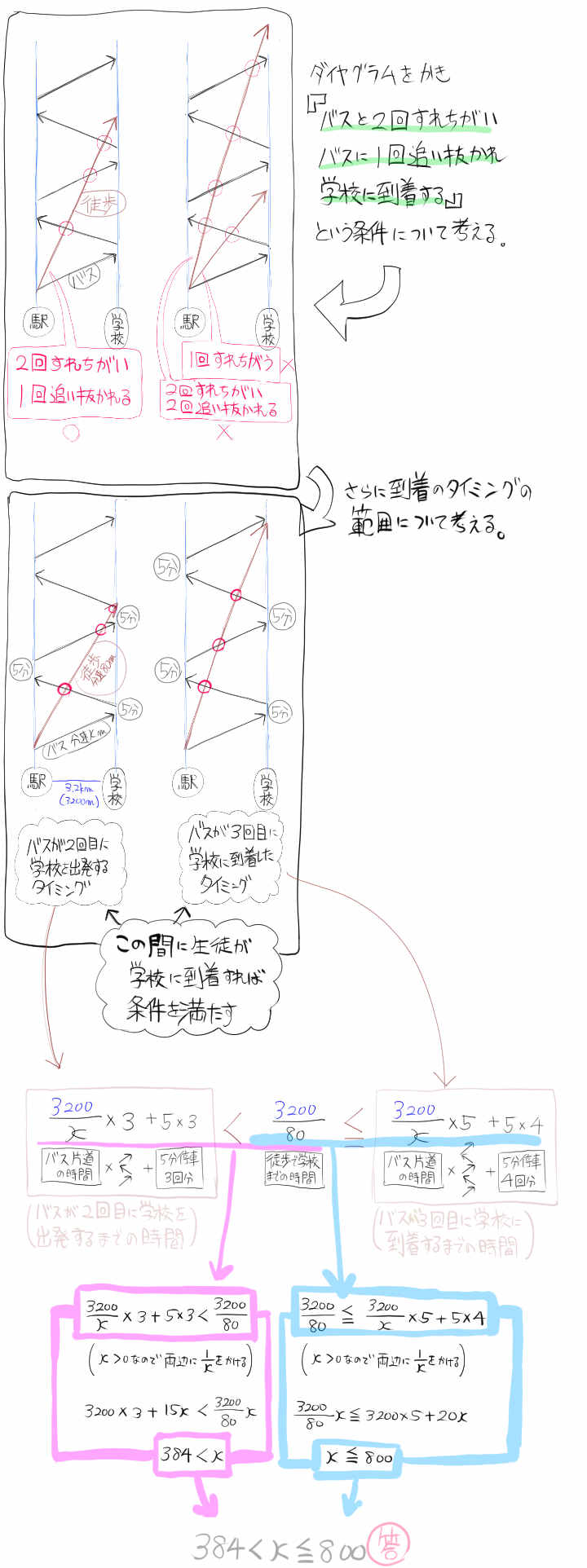
すれ違いや、追い越し、追い抜かれの回数を取り扱うこのような問題の場合、ダイヤグラムによって状況を整理だてて考えると、見通しが付きやすい場合があります。


































