- たすきがけによる因数分解のやり方をわかりやすく解説
- たすきがけの練習問題
- たすきがけを利用した因数分解の応用問題
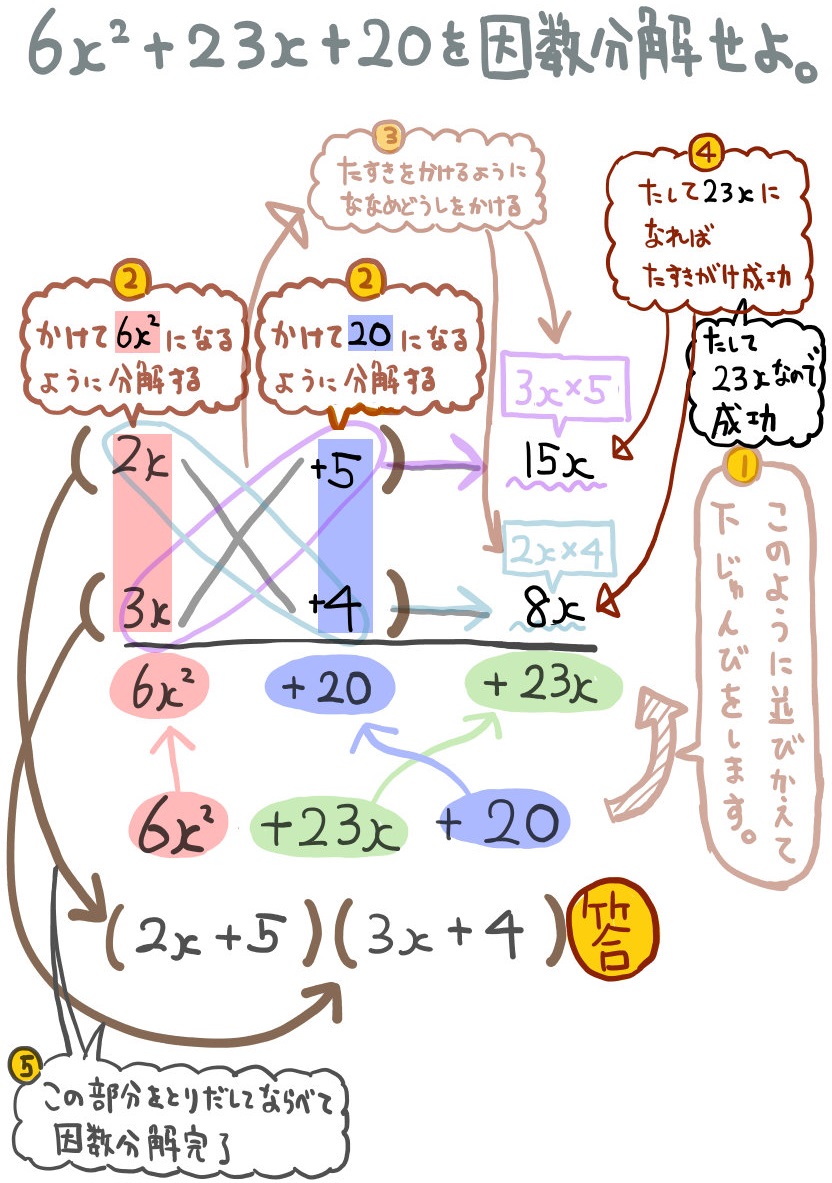
たすきがけによる因数分解のやり方をわかりやすく解説
\(6x^{2}+23x+20\) の式について \(6x^{2}+20+23x\) の順に並びかえます。
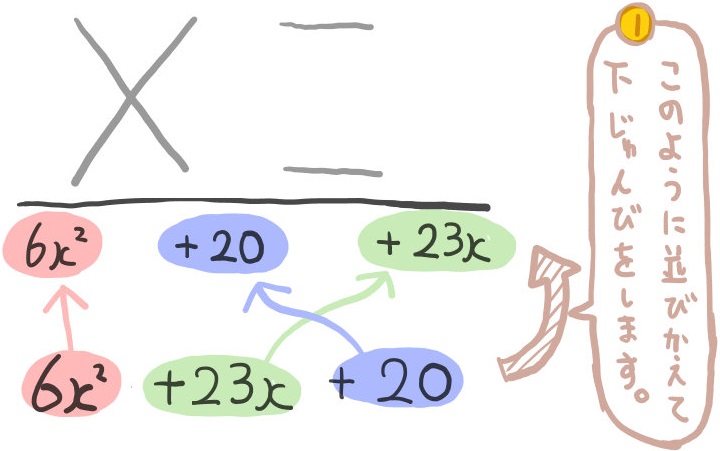また、上の図にあるような筆算の準備になる線を書いておきます。（これで下準備完了！）
\(6x^{2}+20+23x\) の中にある\(6x^{2}\)と２０について、因数分解します。
つまり、かけて\(6x^{2}\)になるように、○×○のかたちに分解します。
この説明図では、\(6x^{2}\)を２ｘと３ｘに分解しました。
２ｘと３ｘはかけて\(6x^{2}\)になりますよね。（こんな感じで分解します）
また、２０も、かけて２０になるよう、ふたつに分解します。
この説明図では、１０と２に分解していますね。（かけて２０になりますよね。）
さきほど分解した値について、たすきをかけるようにして斜めどうしの値を掛け算します。
たすきがけという呼び名がある理由はココですね。
斜めどうしを掛け算した結果を二つ書き込みましたね。
今度はこの２つを合計します。
この合計の値が、緑の部分になれば、たすきがけ成功です。
この例題の場合だと、２３ｘになれば成功です。
２３ｘじゃない！
たすきがけが上手くいかない場合
手順２：\(6x^{2}\)と２０を分解する
の工程で、まちがった分解の仕方をしていた、ということになります。
なので、分解のパターンをかえてみましょう。
その結果、ななめに掛け合わせた数値の結果も、１５ｘと８ｘというように違った結果になりました。
１５ｘと８ｘをたして２３ｘになったので、たすきがけが上手くいきましたね。
たすきがけが成功したら、因数分解を完了させます。
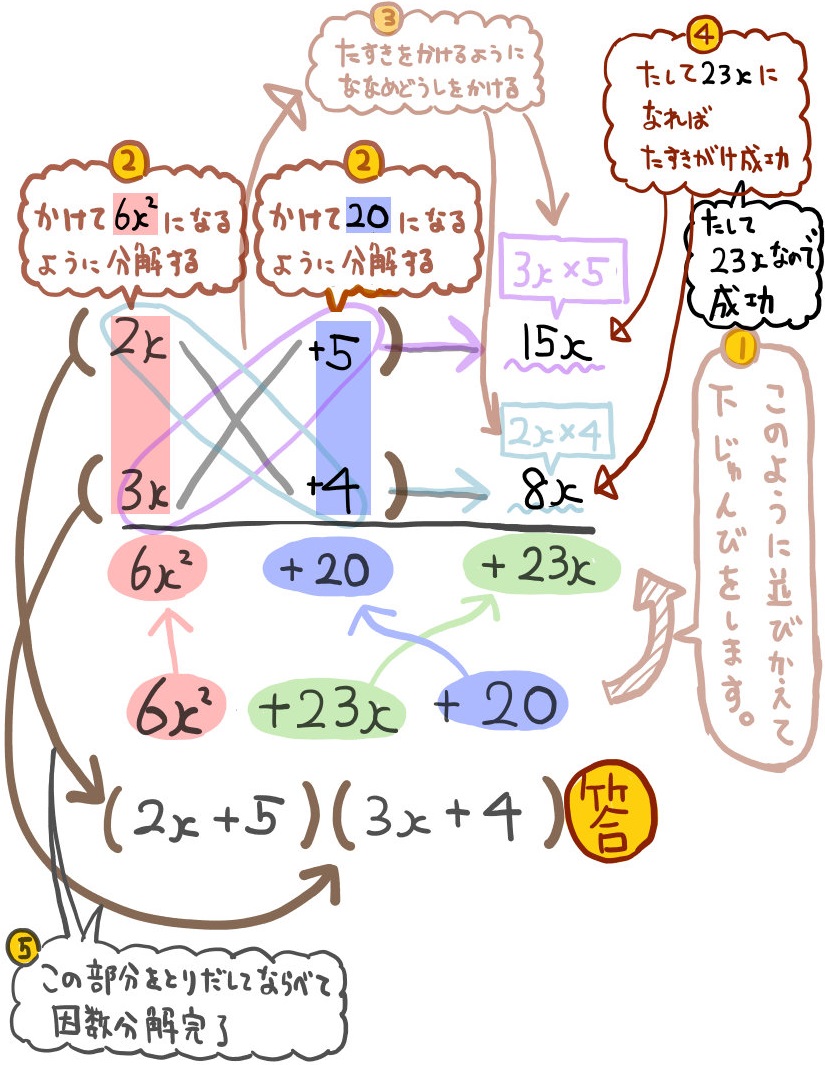
上の説明図にある通り取り出して、因数分解のかたちに並べて完成です。（完）
こちらの動画にて『たすきがけでなぜ因数分解ができるのか？』の理屈の部分と、たすきがけを利用した因数分解の応用問題も解説しています。
たすきがけの練習問題
たすきがけを利用した因数分解の応用問題
- \(x^{2}+\left( 2y-3\right) x-\left( 3y^{2}+y-2\right) \)
- \(x^{2}-2y^{2}-z^{2}+3yz-xy\)
- \(4x^{4}-37x^{2}y^{2}+9y^{4}\)
- \({\small a^{3}b-ab^{3}+b^{3}c-bc^{3}+c^{3}a-ca^{3}}\)
ｘとｙの二次式をたすきがけをするときは、この式の最初の形のように降べきの順に整理します。
『なんとかｘの二乗、なんとかｘ、なんとか』といった形ですね。
それからｘがついていない部分をたすきがけによって因数分解して、最後に式全体でたすきがけをします。
この練習問題のように、最初から降べきの順にきれいに整理されている場合はいいのですが、そうでない場合は、次数の低い文字について、降べきの順に揃えるといいでしょう。
（松山大学：改）
これも先程と同様の手順で因数分解する問題ですが、ｘについての降べきの順に揃える手間が加わっています。(広島女学院大学)
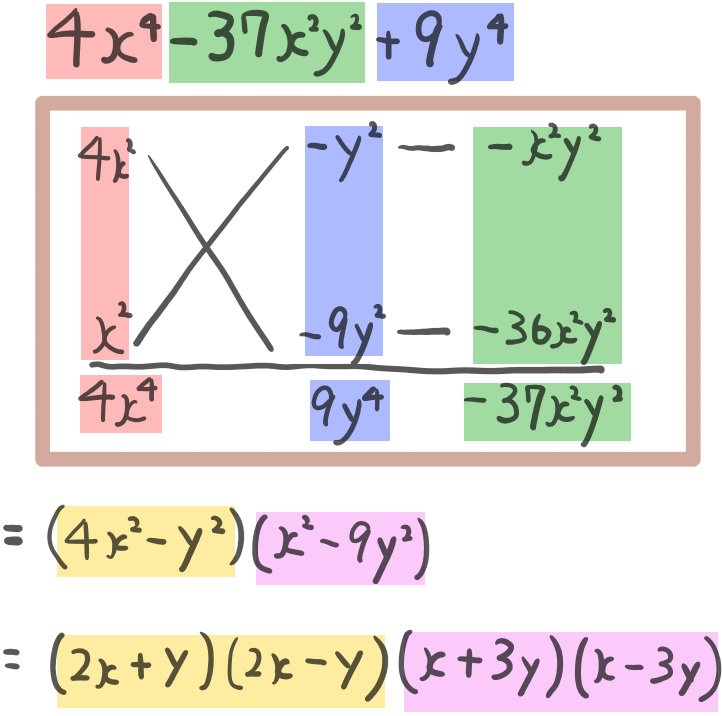
この解法でもいいですが、
\(x^{2}=X\)
\(y^{2}=Y\)
と置いてから、たすきがけをすると、よりわかりやすいかと思います。
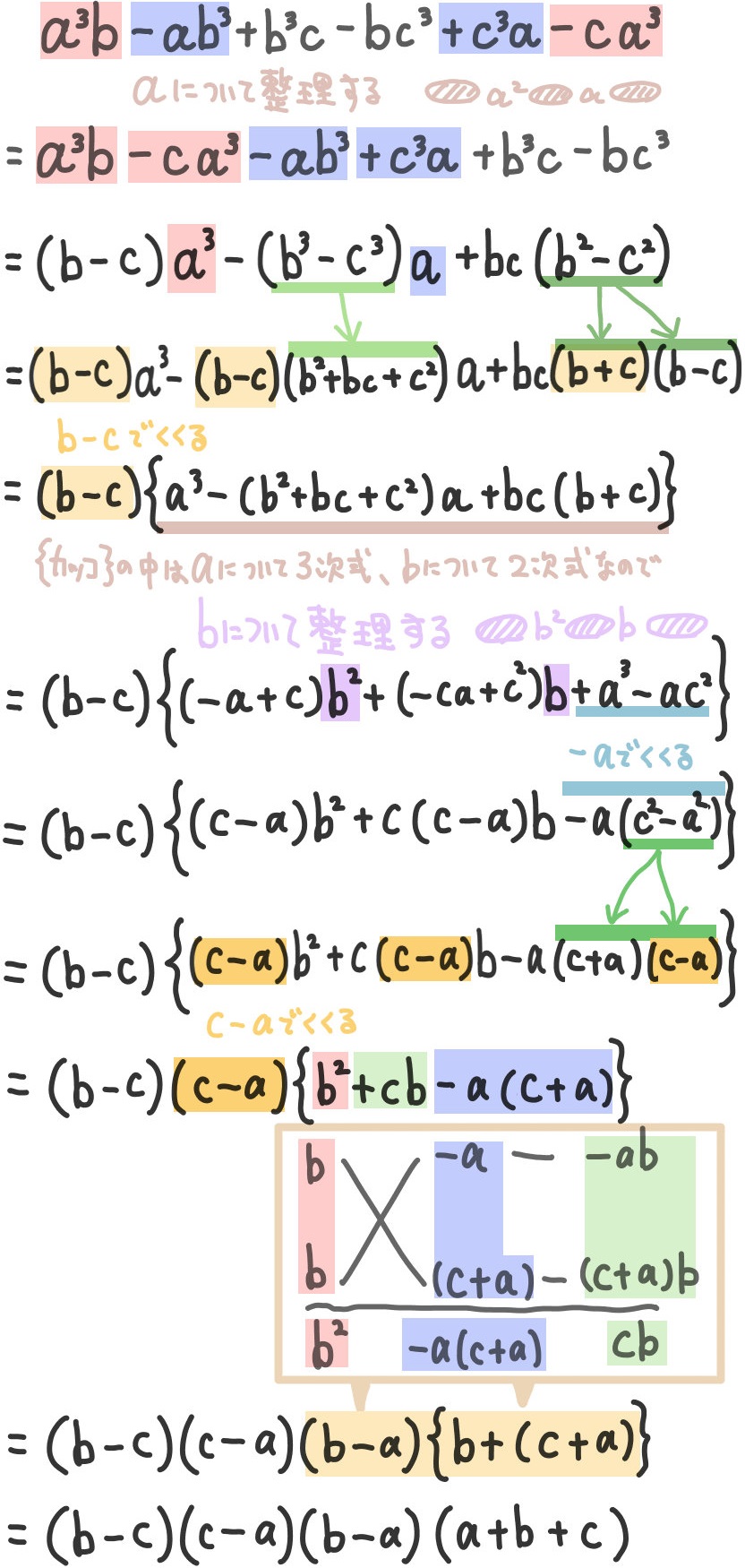
解く途中で、次数の低い文字ｂについて降べきに順に整理するところがあります。
ここはaについての次数が３で、bについての次数が２なので、bについて降べきの順に整理し、因数分解をしています。
最後にたすきがけをしていますが、このページで最初に紹介した説明図のように、 \(x^{2}\) や \(x\) を省略しないたすきがけのやり方がおすすめです。
このほうが、他の文字が登場したり、見慣れない形の因数分解をする際に対処しやすくなります。
（横浜市立大学）
