- ２人同時の仕事量の問題
- 全体を１とおく水槽の問題
- 使用台数と日数を考慮する仕事量の問題
仕事量の問題：方程式の文章題【中１～高校入試】
ある仕事を、Aさんが一人でとりかかると120日かかる。
またBさんが一人でとりかかると72日かかる。
この仕事を、AさんとBさんの二人がかりで同時にとりかかると、何日かかるか求めよ。
ただし二人の仕事量は、二人がかりの時も一人でとりかかった時もそれぞれ同じものとする。
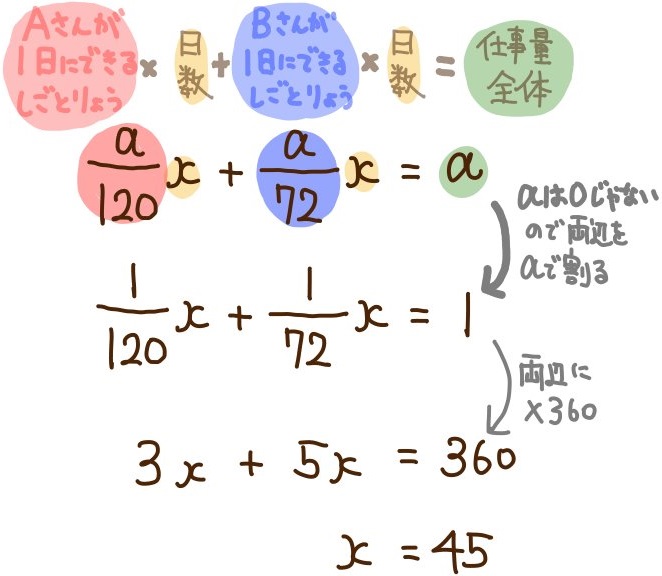
まず、Ａさんが120日がかりでできる仕事量がaということになります。
なのでＡさんが１日にできる仕事量はその120分の1である \(\dfrac{a}{120}\) となります。
同様に考えて、Bさんが１日にできる仕事量は \(\dfrac{a}{72}\) となります。
二人がかりでx日かけて仕事量aを達成したということなので
\(\dfrac{a}{120}x+\dfrac{a}{72}x=a\)
となります。
aは０でないので両辺をaで割ると
\(\dfrac{1}{120}x+\dfrac{1}{72}x=1\)
となり、これを解いて
x=45
となります。
ある水槽に水を入れる。この水槽は、大ポンプだけを使うと４時間で満水になり、小ポンプだけを使うと６時間で満水になる。
この水槽に、はじめは大ポンプだけを使って水を入れていたところ、大ポンプが故障した。
なのでその後、小ポンプだけを使って水を入れ、水槽全体の \(\dfrac{7}{12}\) の量の水を入れるのに３時間かかった。
この時、大ポンプと小ポンプを使用した時間をそれぞれ求めよ。
大ポンプの使用時間は１時間
小ポンプの使用時間は２時間
小ポンプの使用時間をy(時間)
として考えます。
２つのポンプの使用時間の合計は３時間なので
x+y=3
という方程式ができます。
ここで２通りの考え方ができます。
その１：水槽が満水になる水の量をaとおく方法
その２：水槽が満水になる水の量を1とおく方法
それぞれ見てみましょう。
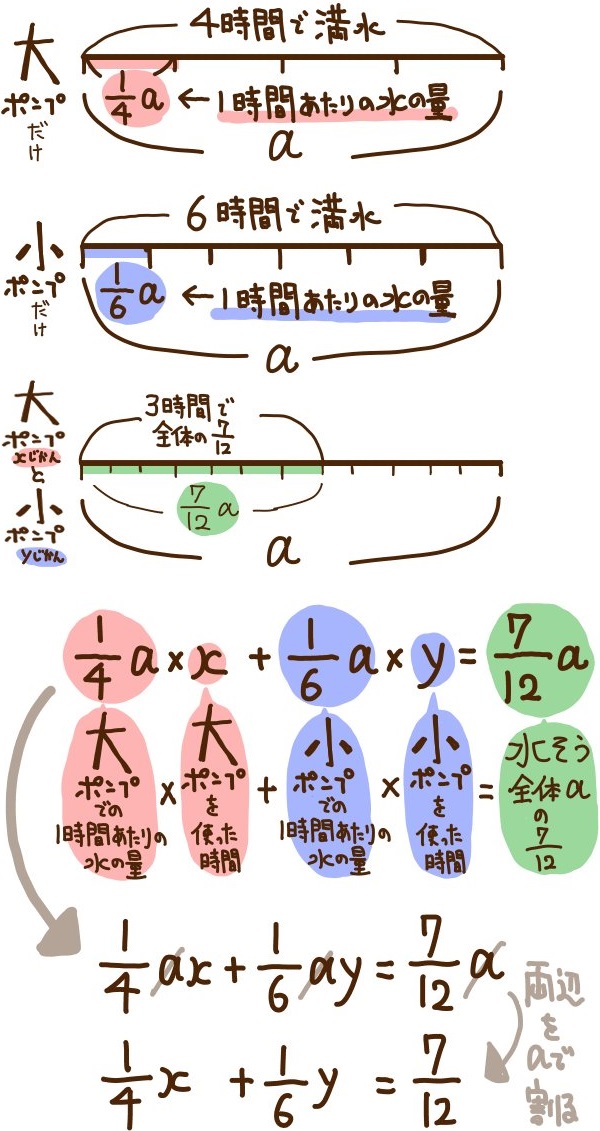※両辺をaで割るとき、aが０でないということを確認しておきましょう。
このようにどちらも同じ方程式が完成します。
これと
x+y=3
とを連立方程式で解き
x=1
y=2となります。
で立式してください。
小ポンプを使用した時間は
３時間－大ポンプを使用した時間
なので、上のような内容になります。
仕事量の問題：連立方程式の文章題【中２～高校入試】
ある製品を１日あたり、それぞれ一定の個数だけ製造できる機械A、Bがある。
この機械Aを２台、Bを１台使って３日間製造し、翌日からAを１台、Bを２台使って、２日間製造したところ、製品が１３４個できた。
また、AとBを１台ずつ４日間にわたって製造し、翌日から機械Bだけを４台使って２日間製造したところ、製品が１５２個できた。
機械Aと機械Bが１日に製造できる製品の個数をそれぞれ求めよ。
機械Aの１日当たりの製造個数は８個
機械Bの１日当たりの製造個数は１０個
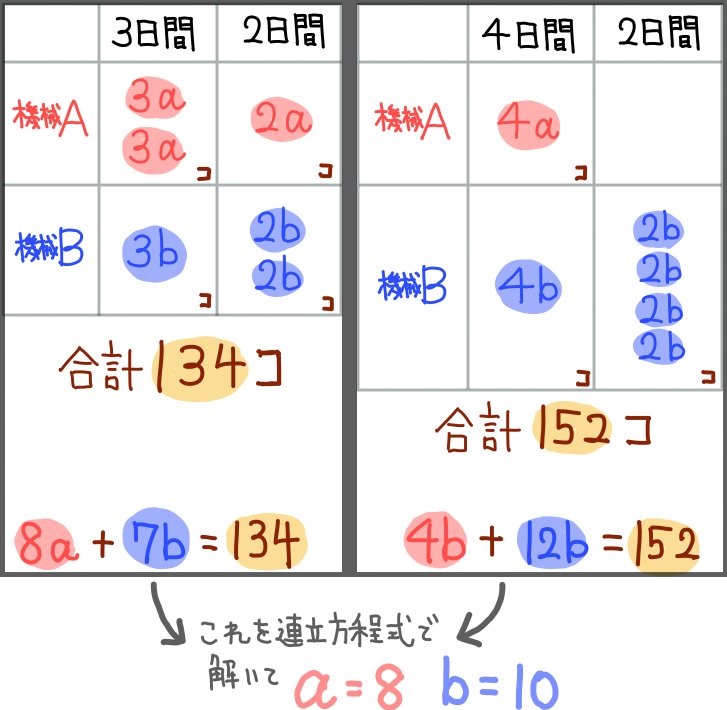機械Aが１日に製造できる個数がa個なので、機械Aが２日で製造できる個数は2a個というように考え、上の表のようになります。
例えば機械Bを４台使用し、それで２日間製造した場合は、2b×4=8b個製造される、というように考えます。
それによってできた連立方程式を解き、aとbを求めて完了です。
