


- 2次方程式の利用の基本~標準問題
- 2次方程式の利用|応用問題・難問
2次方程式の利用の基本~標準問題


n角形の対角線は全部で\(\dfrac{n\left( n-3\right) }{2}\)(本)である。
対角線が35本である多角形は何角形か。

1からnまでの連続する自然数の和は\(\dfrac{1}{2}n\left( n+1\right) \)である。
和が55になるのは1からいくつまでの自然数か。

大小2つの整数がある。この2数の差が7で積が60であるとき、2つの整数を求めなさい。



連続する2つの正の整数がある。
この2数を、それぞれ2乗した数の和が181になるとき、この2数を求めなさい。



連続する3つの自然数がある。
最も大きい数と、最も小さい数の積は、3つの数の和より17より大きい。
これら3つの自然数を求めなさい。



周の長さが34㎝で面積が70㎠である横長の長方形の縦と横の長さを求めなさい。


横の長さは\(\dfrac{34}{2}-x=17-x\)(㎝)と表せる。

\(x=7\)のとき、縦の長さは\(7\)㎝、横の長さは\(17-7=10\)(㎝)で、問題に適している。
\(x=10\)のとき、縦の長さは\(10\)㎝、横の長さは\(17-10=7\)(㎝)で、横長の長方形にならず、問題に適していない。
答:縦7㎝、横10㎝
次の図のような、縦10㎝、横20㎝の長方形ABCDがある。
点Pは、毎秒1㎝の速さで辺AB上をAからBまで進む。
点Qは、毎秒2㎝の速さで辺AD上をDからAまで進む。
2点PQが同時に出発するとき、△APQの面積が24㎠になるのは何秒後か。






 図のように、縦4m、横10mの土地に、同じ幅の道路を作り、残りを畑にしたい。
図のように、縦4m、横10mの土地に、同じ幅の道路を作り、残りを畑にしたい。
畑の部分の面積の合計が16㎡になるには、道路を何mにすればよいか。


 横が縦より5㎝長い長方形の紙がある。
横が縦より5㎝長い長方形の紙がある。
この紙の4すみから1辺が3㎝の正方形を切り取り、直方体の容器を作った。
容器の容積が108㎤であるとき、紙の縦の長さは何㎝か。



 このカレンダーの中にある数を\(x\)とする。
このカレンダーの中にある数を\(x\)とする。
\(x\)の左どなりの数と\(x\)の真下の数をかけた数は、\(x\)に22をかけて62をひいた数と等しくなる。
ある数\(x\)を求めなさい。



ボールを地上から秒速40mで真上に投げ上げる。
投げ上げてから\(x\)秒後のボールの高さは、地上から\(\left( 40x-5x^{2}\right) \)(m)であるとする。
(ⅰ)地上からの高さが75mになるのは、ボールを投げ上げてから何秒後か。
(ⅱ)投げ上げたボールが再び地上に戻ってくるのは、ボールを投げ上げてから何秒後か。







2次方程式の利用|応用問題・難問


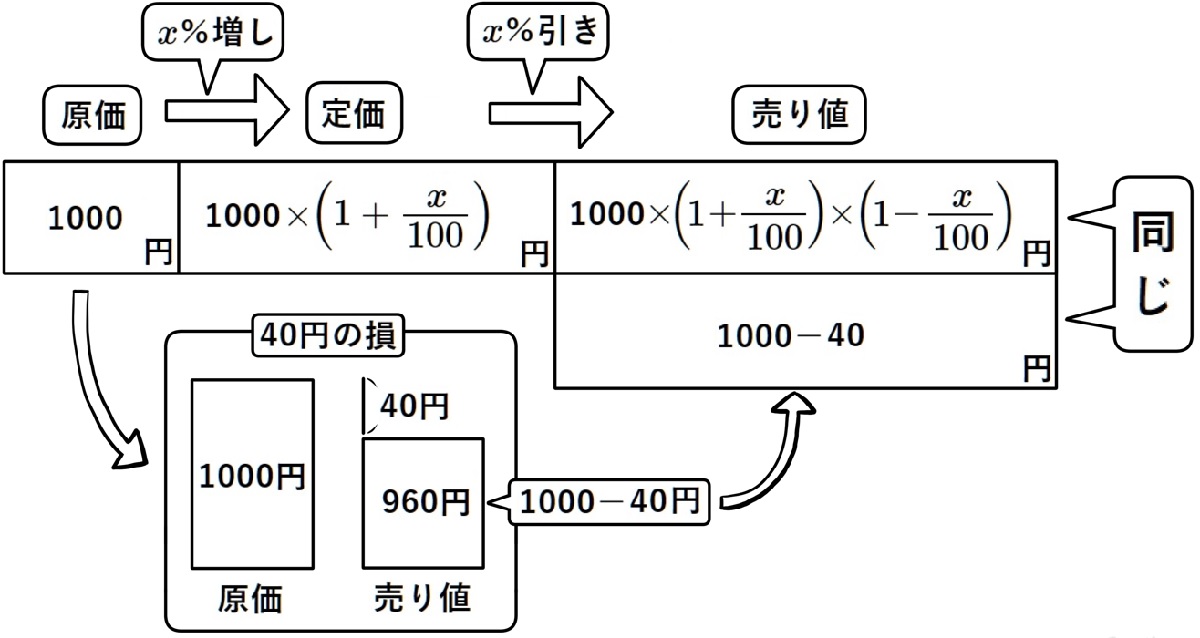
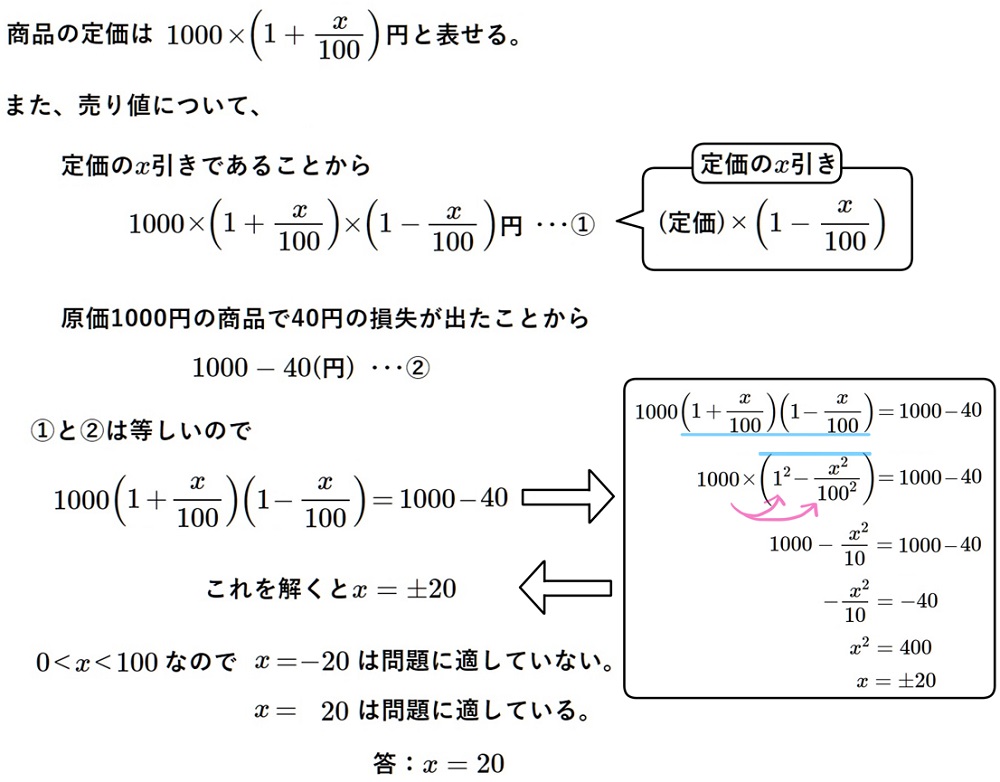
原価1000円の商品に\(x\)%の利益を見込んで定価をつけたところ、売れなかったので、
定価の\(x\)%引きにするとすぐ売れた。その結果40円の損をした。\(x\)の値を求めなさい。

できれば過去問を解いてみて、出題される可能性があるかどうかがチェックできるのが一番です。
対策が必要かどうか不明な場合は、次の問題以外をひとまずマスターすることをおすすめします。
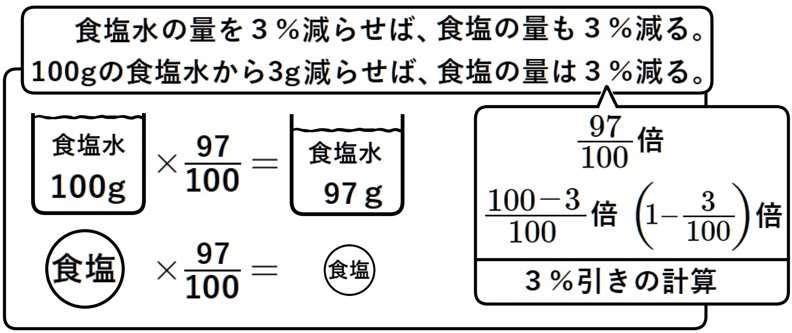
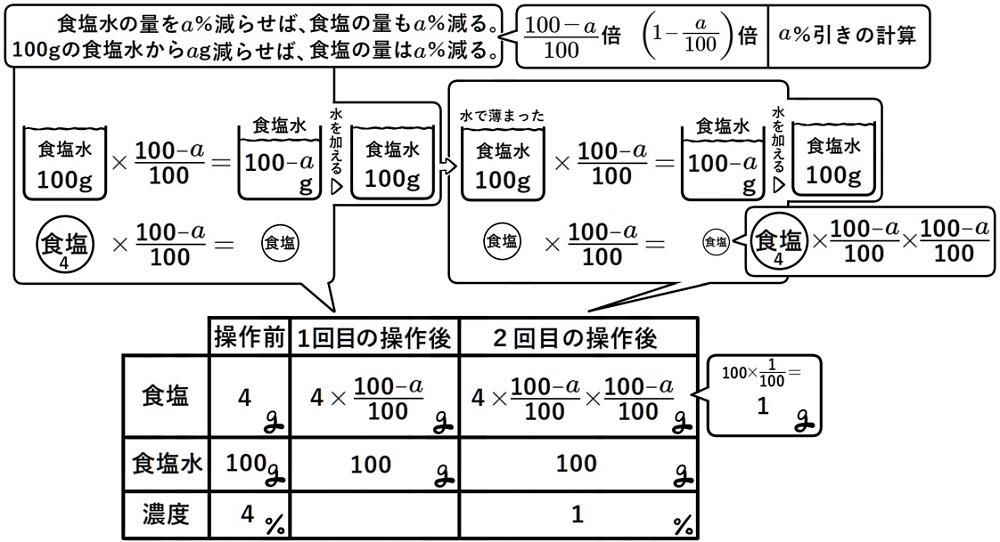
濃度4%の食塩水100gに対し、次の操作を2回繰り返した結果、濃度が1%になった。
操作:食塩水を\(a\)g取り出し、かわりに\(a\)gの水を加える。
このとき、\(a\)の値を求めなさい。



↓
100gの食塩水から\(a\)g取り除いた場合、食塩水に含まれる食塩の量は\(a\)%減る。
食塩水が100gの場合、この考え方を使う場合があります。







































青色の問題:その次にマスターしてほしい問題