

にゃんこ
2次関数のグラフの頂点の座標を求める方法は、主に次の3つの方法があります。

坂田先生
ここでは、平方完成しないで求める方法のなかでも、3番の『x座標だけ公式を当てはめて頂点を求める方法』を丁寧に解説します。

にゃんこ
頂点の座標を求める方法のなかでも、この方法が一番簡単な方法だと思っています。
平方完成をしないで2次関数のグラフの頂点の座標を求める方法

坂田先生
具体的な問題で解説したほうがわかりやすいと思いますので、こちらを題材に説明します。
問題
2次関数 \(y=x^{2}+6x+1\) のグラフの頂点の座標について、平方完成をしないで求めなさい。
求め方
まず、2次関数の頂点のx座標を、公式によって求めます。

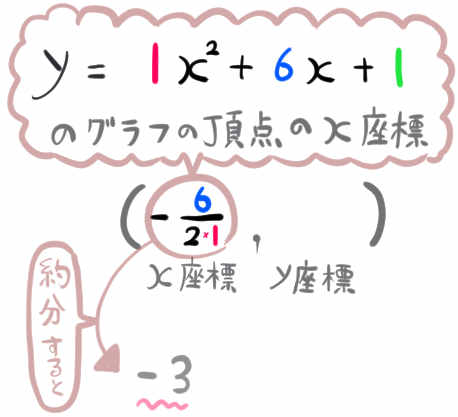
2次関数のグラフの頂点のx座標の公式

公式を問題にあてはめて求めると、頂点のx座標はこうなります。

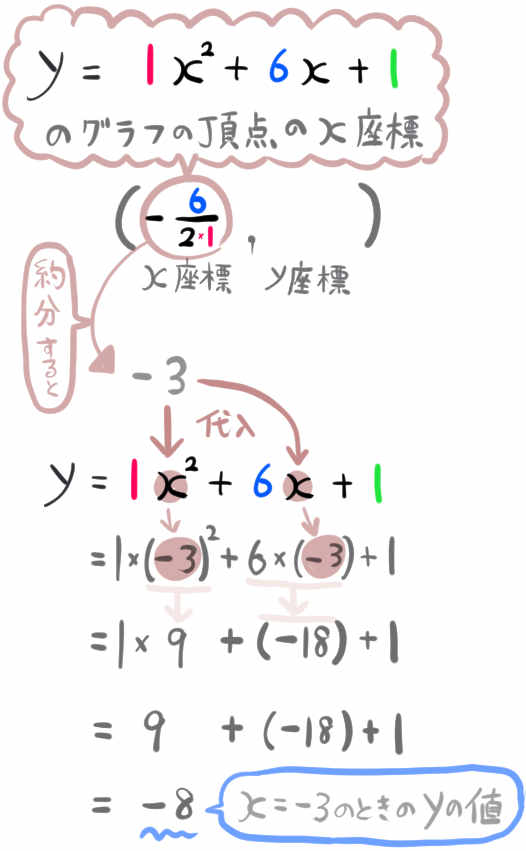
2次関数の頂点のx座標が \(-3\) となったということは、xが\(-3\) の値をとるときのy座標が、頂点のy座標だということになります。
なので、次にやることは、このx座標の値\(-3\) を2次関数のxに代入して、xが\(-3\) のときのyの値を求めることです。

よって、2次関数 \(y=x^{2}+6x+1\) のxの値が\(-3\) のときのyの値は\(-8\) だということがわかりました。
これは2次関数 \(y=x^{2}+6x+1\) の頂点のx座標とy座標のことなので、この2次関数のグラフの頂点の座標は \(\left( -3,-8\right)\) だということが判明したことになります。

坂田先生
以上が『平方完成をしないで、2次関数のグラフの頂点の座標を求める具体的な方法』になります。

にゃんこ
続いてこの手順を慣れるために、実際に練習してみましょう。(同じような解説図で答え合わせができます)
平方完成をしないで2次関数の頂点を求める練習問題

坂田先生
この問題で練習してみましょう。
問題
次の2次関数のグラフの頂点の座標を平方完成をしないで求めなさい。
\(y=4x^{2}+8x\)
解き方のコツ&解答
先程と同じ手順で解いてみましょう。
先程の問題とは少し違って、cにあたる部分がありません。
しかし、頂点のx座標を求めるのにcは使いませんので、やり方は同じままで求められます。
習得のコツですが、最初は慣れないうちは考え込まずに、答えを見ながらなぞるようにして、最後まで解いてください。
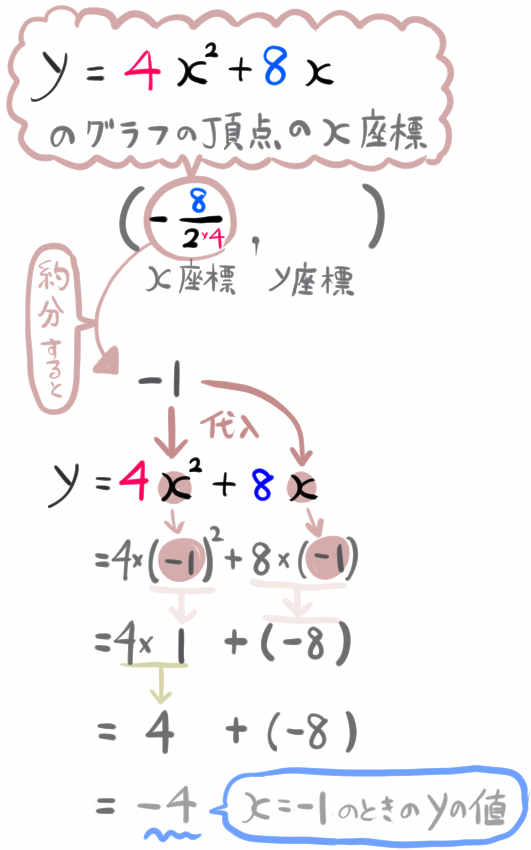
解答はこちらになります。
答え:頂点の座標は \(\left( -1,-4\right) \)


坂田先生
ちなみにこういった『解き方の手順を習得するのが目的』といった問題の勉強法のコツはこうです。
勉強の上手な子の習得方法
1:考えこんで手がとまるなら、すぐに答えを見る。
2:答えを見ながら手を動かす。
3:同じ問題を3回、4回と繰り返して、だんだんとスラスラ解けるようになってゆく。

にゃんこ
逆に言いますと、これはやってはいけません。
やってはいけない、習得方法
1:まだ知ったばかりで慣れていないのに、考え込んで時間を使う。
2:わからないのに、答えを見ようとしないで、自力を突破しようとして時間が過ぎる。
3:1回解いて終わり。繰り返さない。

坂田先生
もしもこんな勉強方法をしていたら、ギクッとしてください。
以上、『平方完成をしないで2次関数のグラフの頂点の座標を求める方法』の解説でした。




































2:平方完成しないで求める方法(x座標、y座標ともに、公式を当てはめる方法)
3:平方完成しないで求める方法(x座標だけ公式を当てはめる方法)