







食塩水の濃度の問題:基礎レベル
6%の食塩水Aと12%の食塩水Bをそれぞれ何gずつ混ぜると、濃度10%の食塩水が300gできるか?
次のように、食塩水と食塩の重さや濃度が一覧でわかるようにまとめます。
表を見ながら、どこが同じになるだろうかと探します。
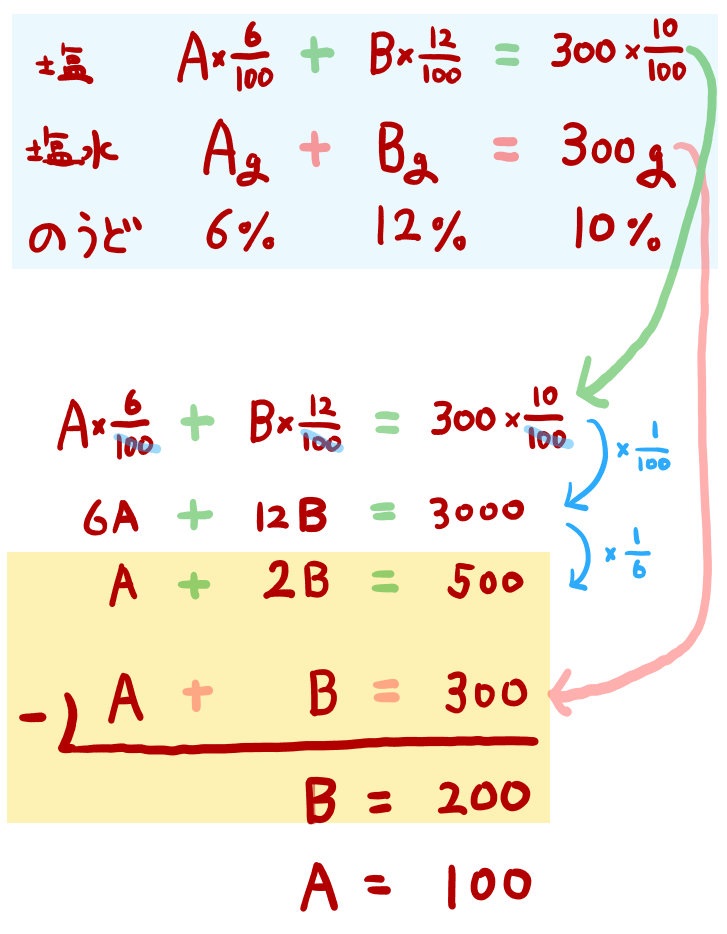

食塩水Bgを、300-A と表してあげれば、Aという文字1種類で方程式を作ることができます。
食塩の重さのところで、このような方程式が完成しますね。

濃度5%の食塩水Aと、濃度のわからない食塩水Bがある。
食塩水Aから400g、食塩水Bから100gを取り出して混ぜ合わせたら、濃度12%の食塩水ができた。
食塩水Bの濃度を求めなさい。
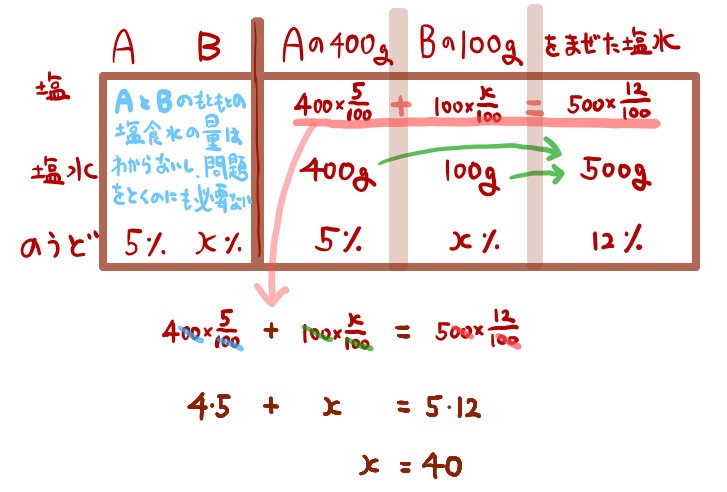 このように基本的には、食塩水で方程式を作り、食塩で方程式を作る、という場合が多いです。
このように基本的には、食塩水で方程式を作り、食塩で方程式を作る、という場合が多いです。濃度は食塩の重さを求める計算に使います。
【ご注意ください】食塩は水100gに36g位まで溶けて飽和してしまう(それ以上解けない状態になってしまう)ので、このx=40を吟味した結果「ありえない」となります。(問題の設定が間違っていました。すみません。)
立式の工程を学ぶ参考としてください。
食塩水Aを400gと、食塩水Bを400g混ぜると、濃度3%の食塩水ができた。
食塩水Aを200gと、食塩水Bを300g混ぜると、濃度2.5%の食塩水ができた。
食塩水A、Bの濃度をそれぞれ求めなさい。
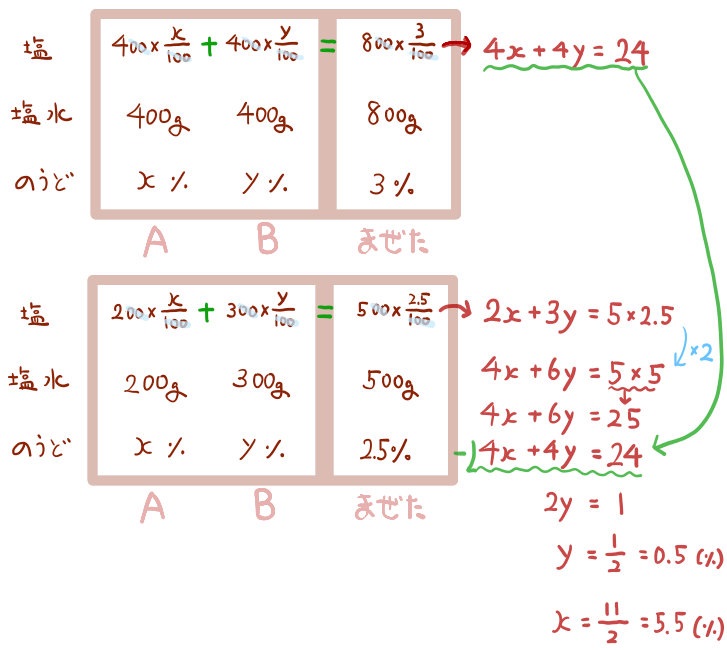 典型的な連立方程式のパターンです。2通りの混ぜ方があるので、表を2通り作り、それぞれで方程式を探しましょう。
典型的な連立方程式のパターンです。2通りの混ぜ方があるので、表を2通り作り、それぞれで方程式を探しましょう。そうして発見した2つの方程式を、連立方程式で解いて完了です。
5%の食塩水Aと、15%の食塩水Bをそれぞれすべて混ぜて、そこに100gの水を加えたら、濃度10%の食塩水500グラムができた。
食塩水A、Bはそれぞれ何gだったか?
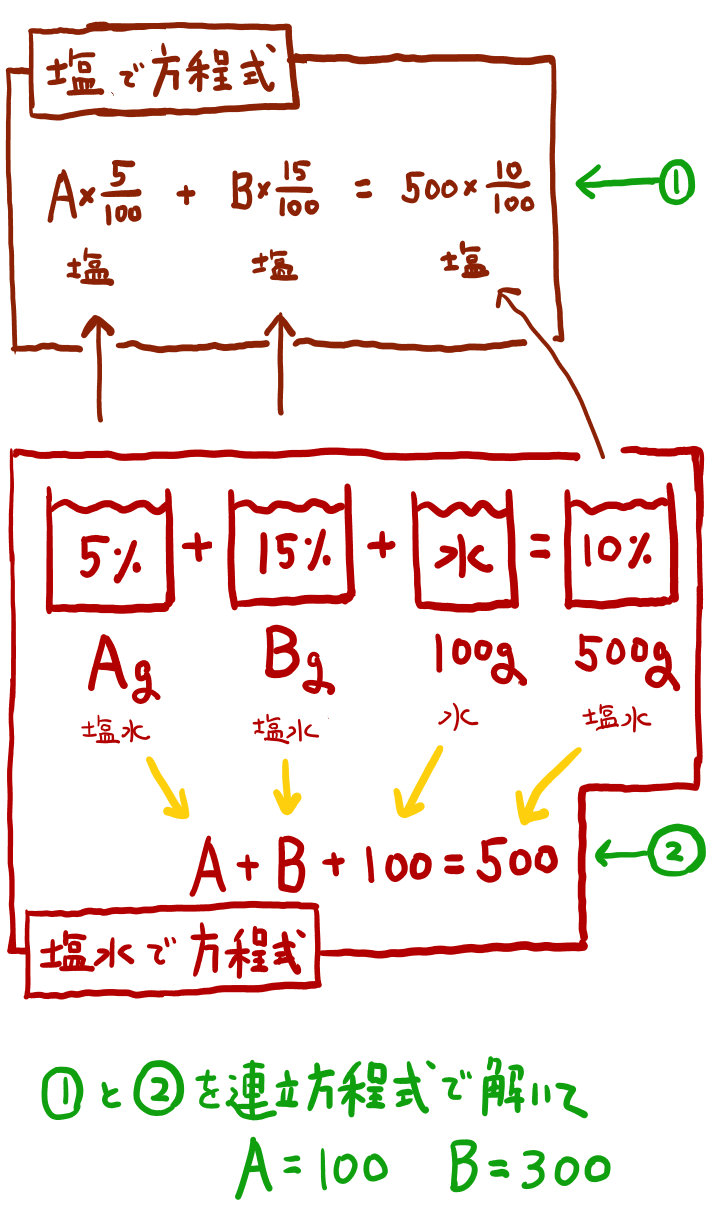 水を加えるということは、水を加えただけ食塩水の重さが増えるということです。また、水を加えても食塩の重さは増えない、という点にも注意しましょう。
水を加えるということは、水を加えただけ食塩水の重さが増えるということです。また、水を加えても食塩の重さは増えない、という点にも注意しましょう。これもまた、食塩の重さで方程式を作り、食塩水の重さでも方程式を作って、連立方程式で答えを求めます。
食塩水の濃度の問題:標準レベル
濃度が異なる400gの食塩水Aと400gの食塩水Bをすべてまぜたら、濃度5%の食塩水ができた。
そこに水200gを加えたら、食塩水Aと同じ濃度になった。
食塩水A、Bの濃度はそれぞれ何%?
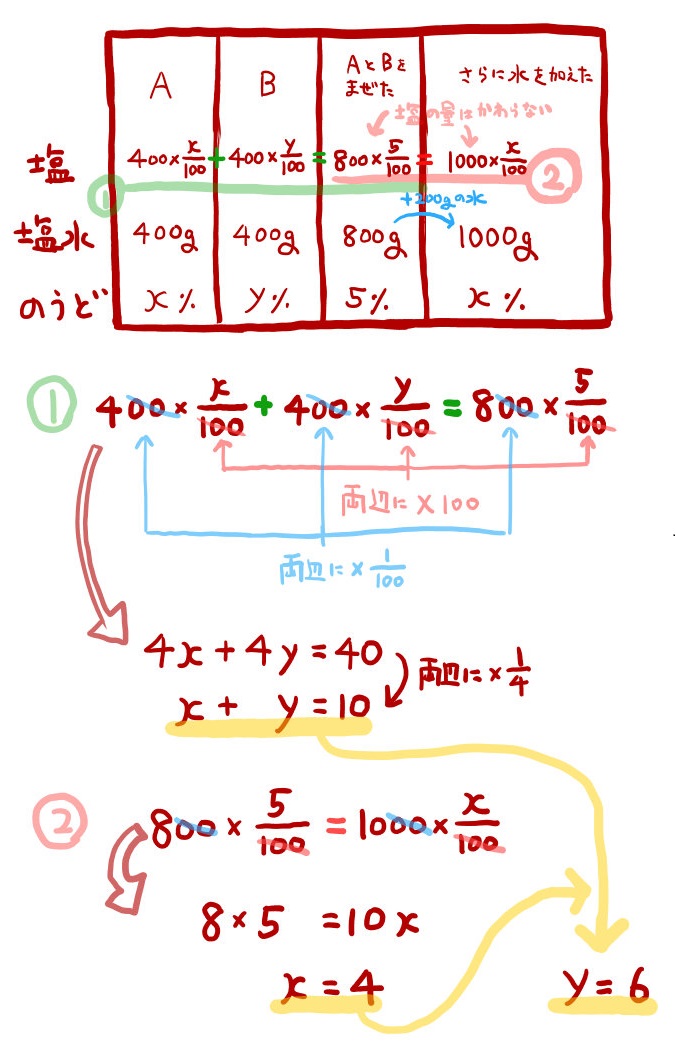 水を加える、ということは、濃度や食塩水の量は変わりつつも、食塩の量は変わらない、ということです。
水を加える、ということは、濃度や食塩水の量は変わりつつも、食塩の量は変わらない、ということです。その点に注目して、表を書き、方程式を発見しましょう。
AとBをまぜた食塩水の塩の量と、そこからさらに水を加えた液体の塩の量は同じになります。(②の方程式)
濃度4%の食塩水Aと、濃度16%の食塩水Bがある。
食塩水Bは食塩水Aよりも40g多い。
食塩水AとBをすべて混ぜ合わせたものに、さらに食塩水Aと同じ重さの水を混ぜ合わせたら、濃度8%の食塩水ができた。
食塩水Aは何gだったか?
 食塩水Aは何gだったか?と聞いているので、そこをxとしましょう。
食塩水Aは何gだったか?と聞いているので、そこをxとしましょう。すると食塩水Bはx+40(g)と表せます。
この二つの液体を混ぜたあとにxgの水を加えるので、このような表にまとめることができます。
濃度5%の食塩水200gに、水170gと食塩を加えて、濃度10%の食塩水をつくりたい。
何gの食塩を加えるとそのようになるか?
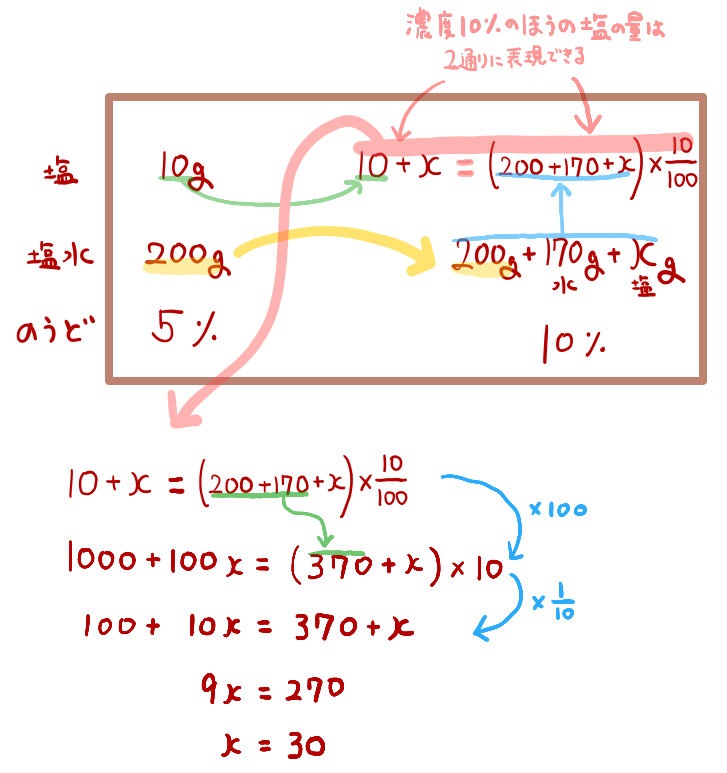 もともと200gの食塩水に水170gと塩xgを加えるのですから、完成した食塩水は200+170+x (g)になります。
もともと200gの食塩水に水170gと塩xgを加えるのですから、完成した食塩水は200+170+x (g)になります。その濃度が10%なので、食塩の重さを式で表すことができます。
その食塩の重さは、水170gと塩を加える前の液体中になった食塩の重さ(10g)よりもxg分増えていることになりますので、10+x(g)とも表すことができます。
この2通りに表した食塩の重さを=でつなぐと方程式の完成です。
濃度16%の食塩水Aと、濃度8%の食塩水Bがある。
食塩水Aの2分の1と、Bの食塩水すべてを混ぜ合わせたら、濃度12%の食塩水800gができた。
食塩水Aと食塩水Bはそれぞれ何gあったか?

食塩水Aのほうは全てまぜないで、その半分だけを混ぜました。
なので、Bの全部とAの半分を合わせて800gの食塩水ができたということです。(方程式②)


↓
Aの半分に含まれている食塩の重さを計算
↓
それを足したものが『まぜた液体に含まれている食塩の量』になる。(1通り目)


濃度が9%の食塩水300gを煮詰めて水を蒸発させ、濃度12%の食塩水をつくりたい。
水を何g蒸発させればよいか。
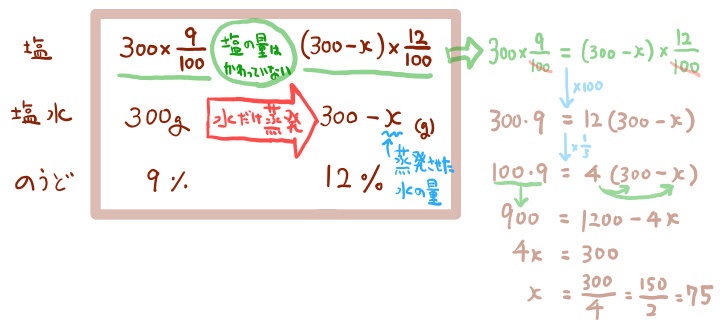
食塩水を煮詰めて水を蒸発させるということは、食塩水の中に含まれる水の量だけ減りつつも、食塩の量はそのまま変わらない、ということです。この点に注目して、水を蒸発させる前の食塩水の塩の重さと、水を蒸発させた後の食塩水の塩の重さを=でつないで方程式を作ります。
食塩水の濃度の問題:やや難問~難問レベル
濃度6%の食塩水Aと、濃度14%の食塩水Bがある。
食塩水Aと食塩水Bを2:3の量で混ぜて、そこに水を加えたところ、濃度9%の食塩水600gができた。
加えた水は何gだったか。
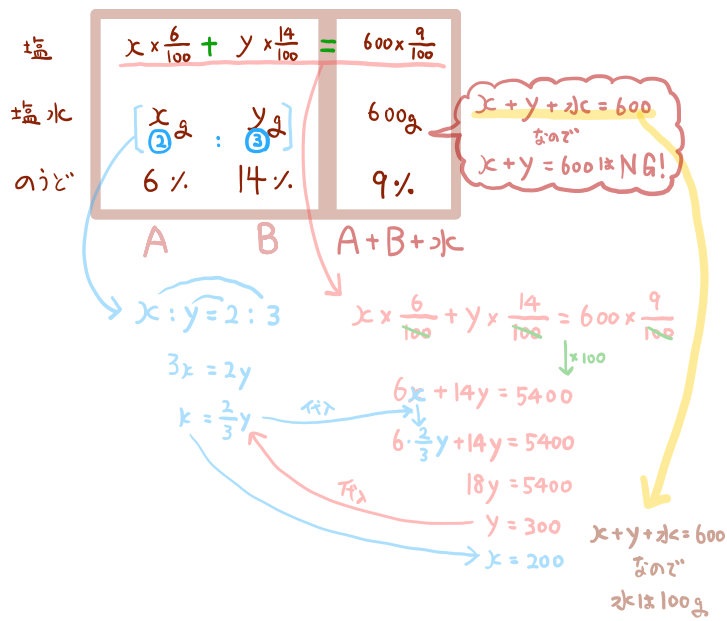
気をつけてほしいのが、x+y=600ではない、ということです。
600gというのは、x+y+加えた水の重さなので、ここでは方程式は作りません。
Aの容器には濃度x%の食塩水400g、Bの容器には濃度y%の食塩水500gが入っている。
AからBへ100gの食塩水を移し、よくかき混ぜた後に、BからAへ200gの食塩水を戻して、よくかき混ぜたところ、Aの食塩水の濃度が7%、Bの食塩水の濃度が8.5%になった。
xとyを求めよ。
なので、難しいと感じた場合は、まずはその練習をしてください。
表を見ながら、どことどこが同じになるだろう?と発見する作業が次の作業になります。




つまり、濃度の文字式が複雑な場合、です。
濃度の文字式が複雑だった時、食塩の重さを文字式で表すことができない、という方はこの説明をご覧ください。

二次方程式を使った食塩水の濃度の超難問

3つの容器A、B、Cがある。
最初、容器A、Bにはそれぞれ100gの食塩水が入っていて、容器A、Bの濃度はそれぞれp%、q%である。
容器Cは空である。
(1)(操作)を1回行ったあとの容器A、Bの食塩水の濃度(%)をそれぞれp、q、xを用いて表せ。
(2)q=10とする。(操作)を1回行うと、容器Aの食塩水の濃度は4%になった。このことを \(x^{2}-x+1=t\) とおいて、Pとtのみの関係式で表せ。
(3)(2)のとき、さらにもう一回(操作)を行うと、容器Bの食塩水の濃度は8%になった。このとき、p、xの値をそれぞれ求めよ。
(灘高校)






































