



時計の長針と短針の速さと角度の問題【暗記事項の計算】


※教材ページはこちら
短針は、24時間で2周します。(午前で1周、午後で1周)
つまり、12時間で1周(360°)します。
1時間は12時間の12分の1なので、360°の12分の1だけ進むということです。
計算すると、1時間で30°ということがわかります。

1時間(60分)で30°進むということは、
1分はその60分の1の時間なので、30°の60分の1だけ進むということになります。
計算すると0.5°となります。

長針は60分で360°(1時間で1周)進みます。
1分はその60分の1なので、360°の60分の1進むことになります。
よって、360°を60で割り、1分で6°進むのだとわかります。

短針は1分間で0.5°進みます。
よって\(x\)分間では、0.5\(x\)°進みます。

長針は1分間で6°進みます。
よって\(x\)分間では、6\(x\)°進みます。

短針が12時間で1周する間に、長針は12周(1時間ごとに1周)します。
なので、長針の進む速さは、短針の進む速さの12倍となります。

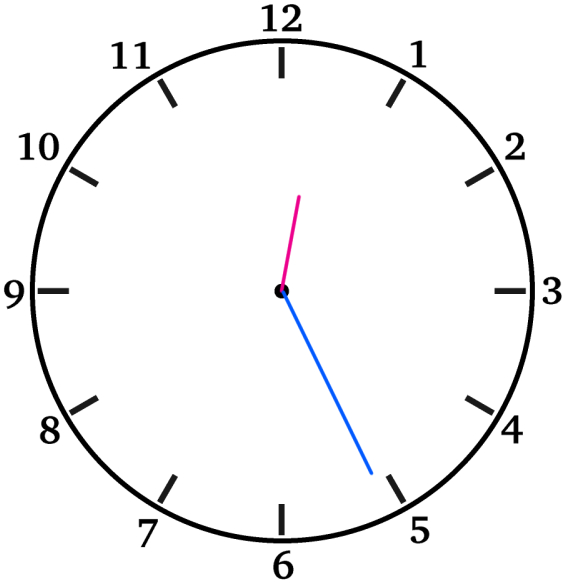
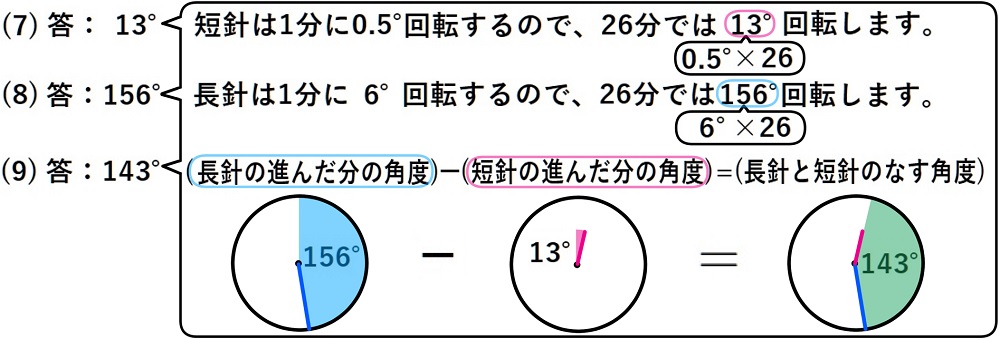
(7)12時26分の短針は、12時の位置から何度右回転した向きにあるか。
(8)12時26分の長針は、12時の位置から何度右回転した向きにあるか。
(9)12時26分の長針と短針のなす180°以下の角度を求めなさい。
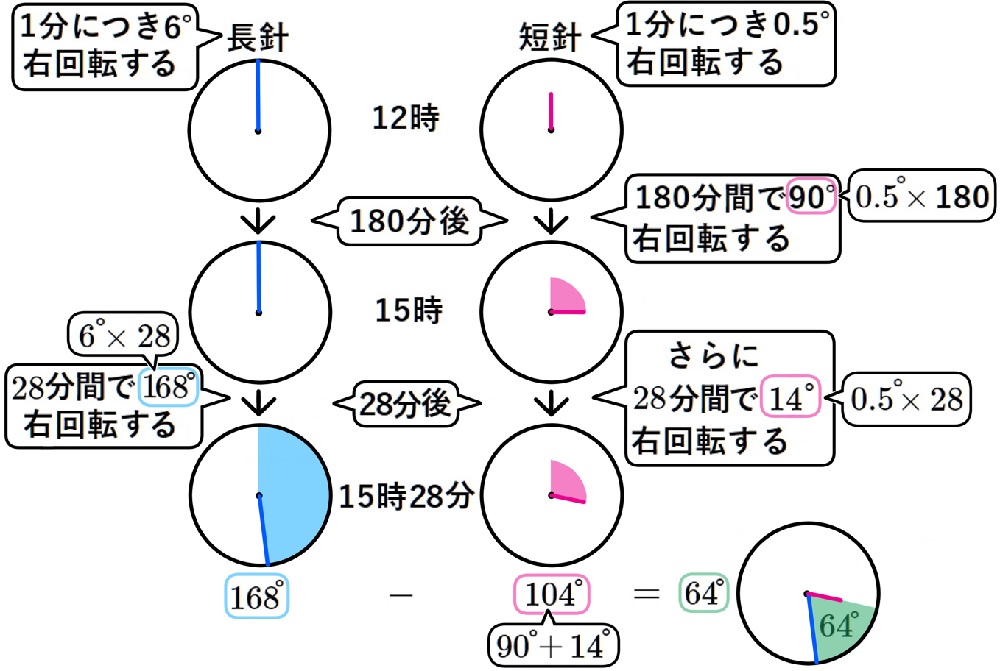
時計の長針と短針がつくる角度の問題【基本~応用問題】中学数学~高校入試



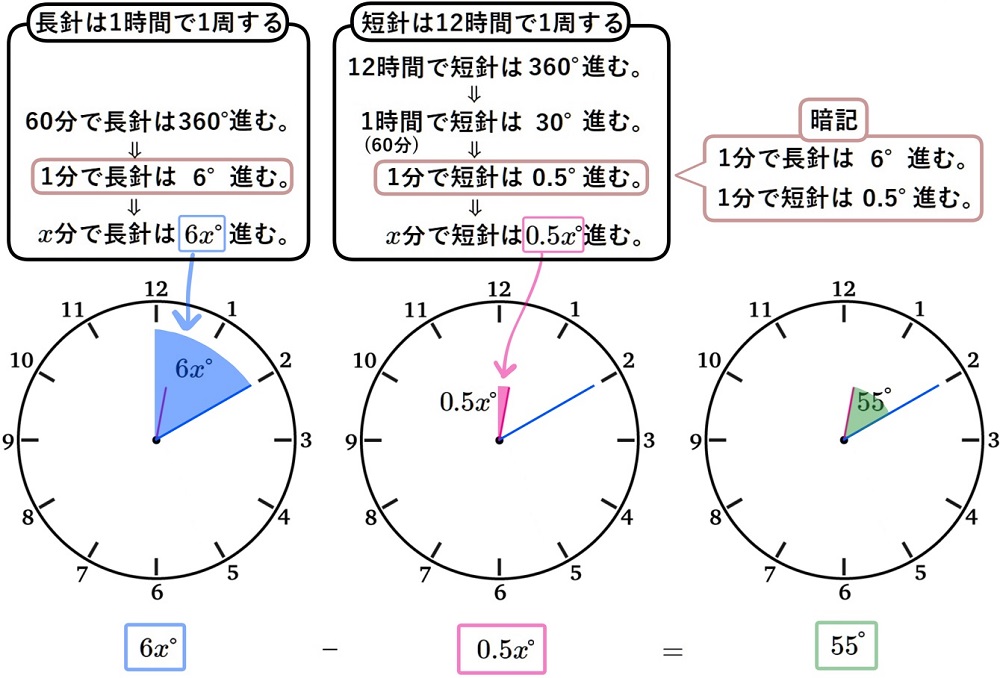
12時\(x\)分において、長針と短針のなす角度が55°になるときの\(x\)の値を求めなさい。

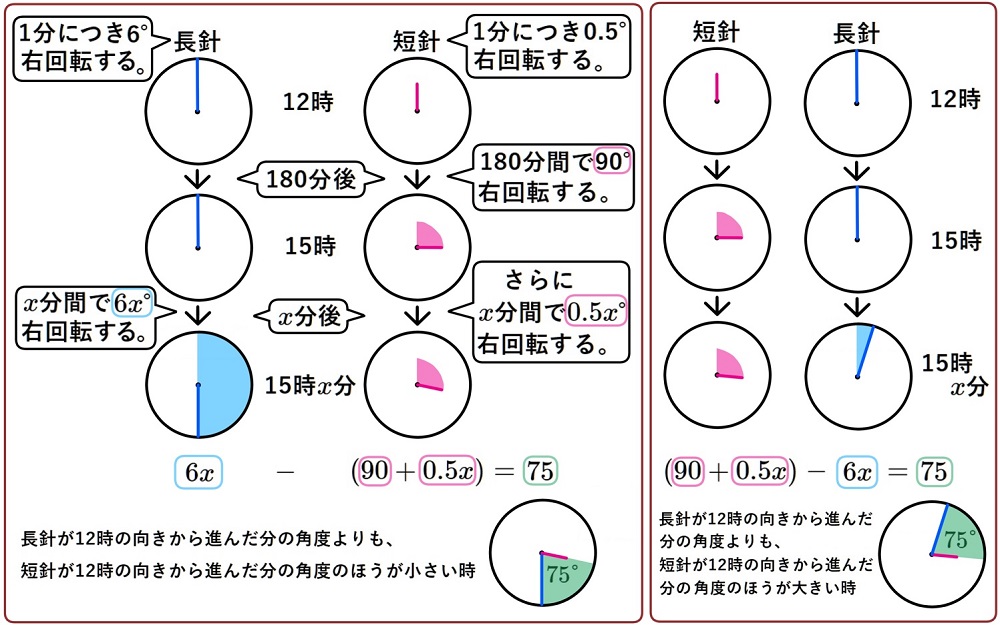
15時\(x\)分において、長針と短針のなす角度が75°になるときの\(x\)の値を求めなさい。※値が分数になるときは帯分数で答えなさい。


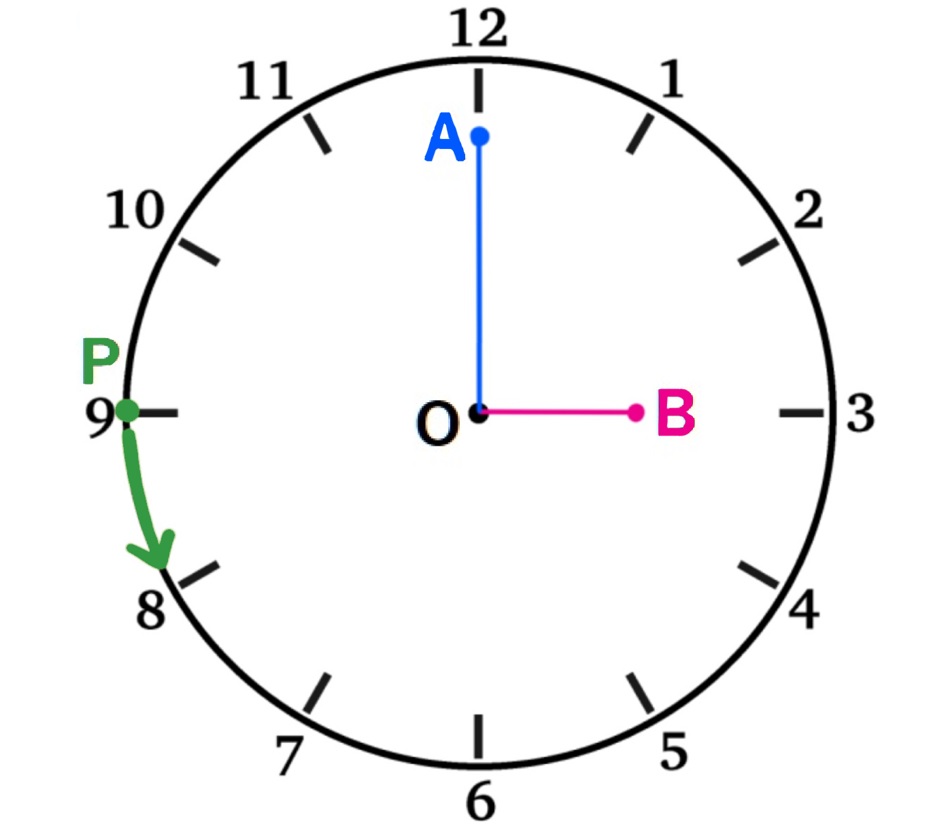 長針の先端をA、短針の先端をBとし、文字盤の中心を点Oとする。
長針の先端をA、短針の先端をBとし、文字盤の中心を点Oとする。
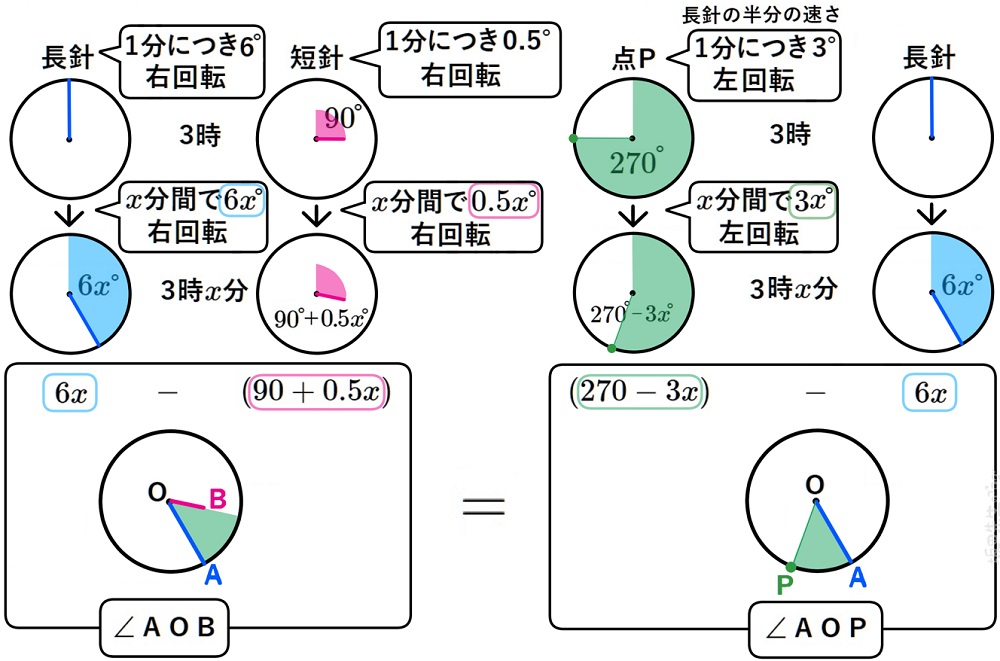
図のように、点Pが午前3時ちょうどに文字盤の9の位置から出発し、長針の進む半分の速さで、反時計回りに時計盤の周りを回るものとする。
午前3時\(x\)分において、次の条件をすべて満たすとき、\(x\)の値を求めなさい。※値が分数になるときは帯分数で答えなさい。
条件1:∠AOB=∠AOPとなる。
条件2:文字盤の12時の位置から右回りにB、A、Pと並ぶ。

時計の長針と短針の角度がテーマの高校入試の過去問

この長針と短針でできる角度a(a≦180)を求めよ。
(B)点Pは午後2時ちょうどに文字盤の9の位置を出発して、次の条件を満たしながら時計の周上を回る。
条件1:回る向きは針の回る向きと逆向きである。
条件2:回る速さは長針の回る速さの半分である。
長針と短針と線分OPが、はじめてこの順に等しい角度の間隔で並ぶのは午後2時何分か求めよ。ただし答えは帯分数の形で答えること。




































アナログ時計の針の向きは、0時00分の時の状態から
・長針は1分で6度進む。
・短針は1分で0.5度進む。
※次の問題(1)~(3)の解説にあるように暗記していなくても導くことができますが、暗記しておくと問題を解く際の時間短縮になります。