- 平方根の応用問題｜難問まで各テーマ別一覧
- 平方根の応用問題の勉強方法｜学習効率の良い優先順位
- 平方根の難問対策に効果的な手順｜解説を読むタイミング
平方根の応用問題｜難問まで各ジャンル別一覧
学習ページはこちら：【難問のみ】工夫で解く平方根の計算問題たち
学習ページはこちら：【難問のみ】平方根のある式の値の問題
学習はこちら：平方根の大小関係と大小比較の練習問題｜難易度別に解説
- 平方根の大小関係を不等号で表す問題パターン
- 平方根の記号を含む不等式に関する問題パターン
【基本】\(-\sqrt{2}\) 、 \(-\sqrt{5}\) 、\(-\sqrt{7}\) の大小関係を不等号で表せ。
【難問】\(5\sqrt{2}\) 、\(7\) 、\(\dfrac{\sqrt{192}}{2}\) 、 \(\sqrt{3}+\sqrt{27}-\sqrt{2}\) の大小関係を不等号で表せ。
【基本】\(\dfrac{7}{2} ＜ \sqrt{n} ＜4\) となるような自然数ｎの個数を求めよ。
【難問】a、nを自然数とする。 \(n≦\sqrt{a}≦n+3\) を満たすaが70個あるときのn値を求めよ。
学習はこちら：平方根の利用｜ルートの中の自然数ｎを求める問題一覧
- 根号の中の最小の自然数ｎを求める問題パターン
- 根号の中の自然数ｎの個数数またはすべての値を求める問題パターン
【基本】\(\sqrt{60n}\) が整数となる最も小さい自然数nを求めよ。
【難問】自然数n、mが\(\sqrt{123+n}=m\sqrt{3}\) を満たすとき、最小のnの値を求めよ。
【基本】\(\sqrt{7n}\) が整数となる100以下の自然数nをすべて求めよ。
【難問】\(\sqrt{120+n^{2}}\) が整数になるための自然数nの個数を求めよ。
学習はこちら：平方根の小数部分と整数部分の問題｜難易度別に解説
- 小数部分に関する問題パターン
- 整数部分に関する問題パターン
【基本】\(\sqrt{20}\) の小数部分を \(x\) とするとき、\(\left( x+1\right) \left( x+7\right)\)の値を求めよ。
【難問】\(\left( \sqrt{3}+\sqrt{5}\right) ^{2}\) の小数部分をxとするとき、\(x^{2}+14x\)の値を求めよ。
【基本】\(\sqrt{n}\)の整数部分が２になるとき、自然数nの値をすべて求めよ。
【難問】\(\sqrt{n}\)の整数部分を\(p\left( n\right) \)とするとき、\(p\left( n\right) +p\left( n+1\right) =4\) を満たす自然数nをすべて求めよ。
このような問題が苦手という方のために用意した『解き方を丁寧に解説したページ』です。
\(\sqrt{15}=3.873\) 、\(\sqrt{1.5}=1.225\)として、次の値を求めなさい。
(1) \(\sqrt{150}\)
(2) \(\sqrt{1500}\)
(3) \(\sqrt{15000}\)
(4) \(\sqrt{0.015}\)
(5) \(\sqrt{0.0015}\)
それはそれはわかりやすくていねいに解説しています。
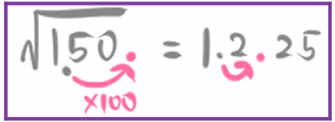
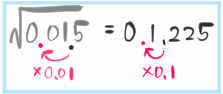
平方根の応用問題の勉強方法｜学習効率の良い優先順位
平方根の難問対策に効果的な手順｜解説を読むタイミング
１：平方根の難問を解いてみようとする。
２：さっぱりわからない場合はすぐに解説を読む。
３：少し考えていけそうな場合は少し考えて、わからなければ解説を読む。
４：解説が理解できた場合、解説の式を見ながら、自分の言葉で説明してみる。
５：日をあけて同じことをしてみる。（復習）
６：スラスラ自分の言葉で解説できるようになったら、解答を再現する練習をする。
７：そのストックを増やしてゆく。（つまり復習もしてゆく）
１：意気揚々と難問にとりかかる。
２：さっぱりわからないのに、長時間考え続ける。
難問を対策しようという場合に効果的なのは、平方根の応用問題のなかでも、同じジャンルの難問だけまとめて解いてゆく、という方法です。
例えば、平方根の小数部分だけが題材に上がっている難問だけをまとめ解く、という具合です。
このように範囲を絞ってそのテーマのみの難問を繰り返し解くと、そのテーマに対する理解力が深まると同時に実力が上がりやすいです。
また、これは平方根の問題に限らず、他の分野でも有効な学習スタイルですので、ぜひ参考にしてください。
学習の優先順位は以下のようになっています。- 平方根の基本の計算問題をスラスラ解ける状態にする
- 大小関係に関する問題を基本レベルまで練習する
- ルートの中の自然数ｎを求める問題を練習する
坂田先生
中学数学の定期テスト対策として取り組みたい場合は、学校で使用しているワーク（問題集）と教科書の章末問題を利用しましょう。
にゃんこ
優先順位としては、練習したいパターンだけをピックアップして解いてゆくと学習効率が良くなります。
これがまず準備できていないと、応用問題や難問にとりかかっても学習効率が悪くなってしまいます。
スラスラ解ける状態になったら、いよいよ応用問題の対策に進みます。
その際、いきなり問題を解くのではなく、解説を読み、その内容がわかるかどうかのチェックをします。
平方根の応用問題に苦手が子が多いのは、ルートに関する基本的な理解が解く際の武器になるため、暗記で突破しにくいという特徴があるからです。
もちろん解き方のパターンに慣れるということは大事なことですが、難問になるほど、ただ暗記すればよいというワケにはいかなくなります。
そういった意味で、大小関係に関する問題は、理解を助けてくれる題材としては相性がよいジャンルになります。
次に平方根の理解を助けてくれるジャンルとして有効なのは、ルートの中の自然数ｎを求める問題です。
ここで、基本レベルまでを繰り返し解いて、パターンに慣れつつ、平方根の応用問題に慣れていきます。
ここまで学習すれば、応用問題を練習してゆく土台は整いました。
近似値の問題や整数部分、小数部分の問題を対策しても良いですし、これまで学習した平方根の問題を難問まで対策していってもいいでしょう。
ただ、繰り返しになりますが、学習の際大事なことは、わからない場合なすぐに解説を読み、その説明が理解できるかどうかのチェックをしてください。
そのことに関して次は『平方根の難問対策』について詳しく解説していきます。