平方根の利用｜自然数ｎを求める練習問題｜中学数学の定期テスト対策など
- \(\sqrt{60n}\) が整数となる最も小さい自然数nを求めよ。
- \(\sqrt{7n}\) が整数となる100以下の自然数nをすべて求めよ。
- \(\dfrac{\sqrt{128n}}{7}\) が整数となるときの最も小さい自然数nの値を求めよ。
- \(\sqrt{\dfrac{3n}{2}}\) が整数となる60以下の自然数nをすべて求めよ。
- \(\sqrt{\dfrac{180-3n}{2}}\) が整数となる自然数nをすべて求めよ。
平方根の部分が整数になるための自然数ｎを求める問題は、まず平方根のなかの数を素因数分解します。
それから、ｎの値を考えます。
平方根の中のｎは『７×整数の二乗』のかたちである必要があります。そのかたちのときにはじめて\(\sqrt{7n}\)は整数となります。なので、『７×整数の二乗』を調べていくと、上のような答えが見つかります。
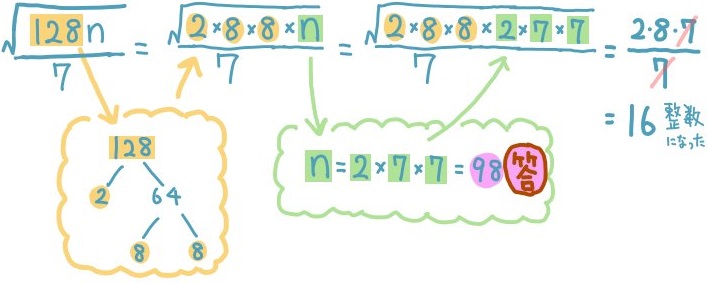このように自然数ｎを求める平方根の問題で、分数のかたちになっている場合は、分母の数を約分によって１にしてはじめて整数となることに注意してください。
この場合は分母の７を約分によって１にする必要がありますので、分子の素因数のなかに、７が含まれている必要があります。
なので、自然数ｎのなかに、７の二乗がある、というワケです。（上の図を見るとその理由がわかりやすいかと思います。）
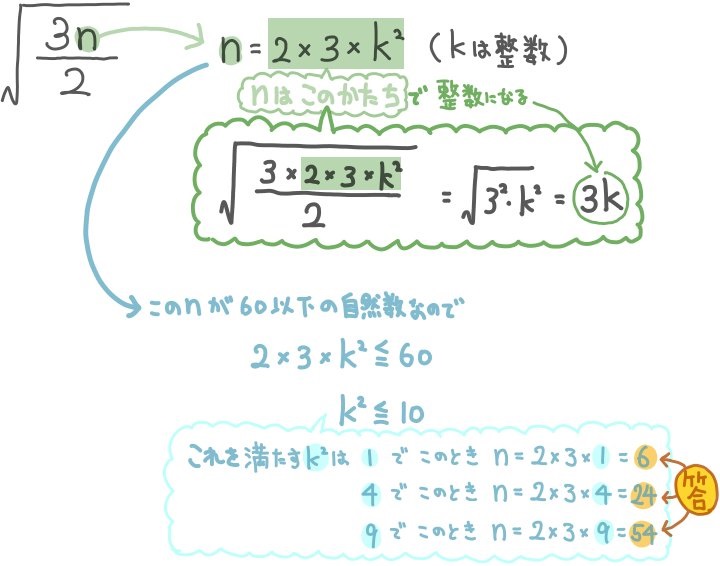このような自然数ｎを求める平方根の分数の問題は、自然数ｎの候補が無限にありますので６０以下という制限がなされています。
中学数学の定期テストでも出題されそうな問題ですが、対策をしておかないと難しく感じてしまいます。
１，４，９，というのはｋの２乗すなわち平方数でなおかつ１０以下の数なので、この３通りを計算したというワケです。
平方根の利用｜自然数ｎを求めるやや難問の高校入試問題
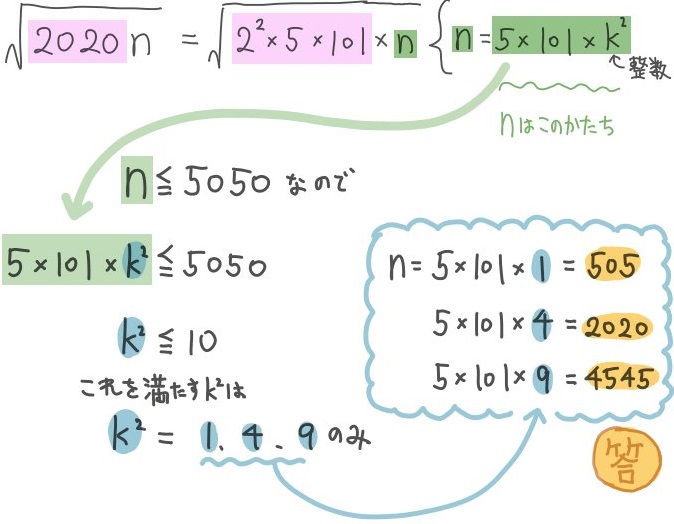
- \(\sqrt{2020n}\) が整数となる5050以下の自然数ｎをすべて求めよ。
- \(\sqrt{\dfrac{2520}{n}}\) が整数となるような自然数nの最小の値を求めよ。
- \(\sqrt{\dfrac{1287}{2n+7}}\) の値が整数となるとき、最も小さい自然数nの値を求めよ。
- \(\sqrt{100-n}\)が素数となる自然数nのうち、その素数が最大の値となるときのnの値を求めよ。
- \(n=1\times 2\times 3\times \ldots \times 7\) とする。 また、mを自然数とする。\(\sqrt{\dfrac{n}{m}}\) が整数となるとき、\(\sqrt{\dfrac{n}{m}}\)の最も大きい値を求めよ。
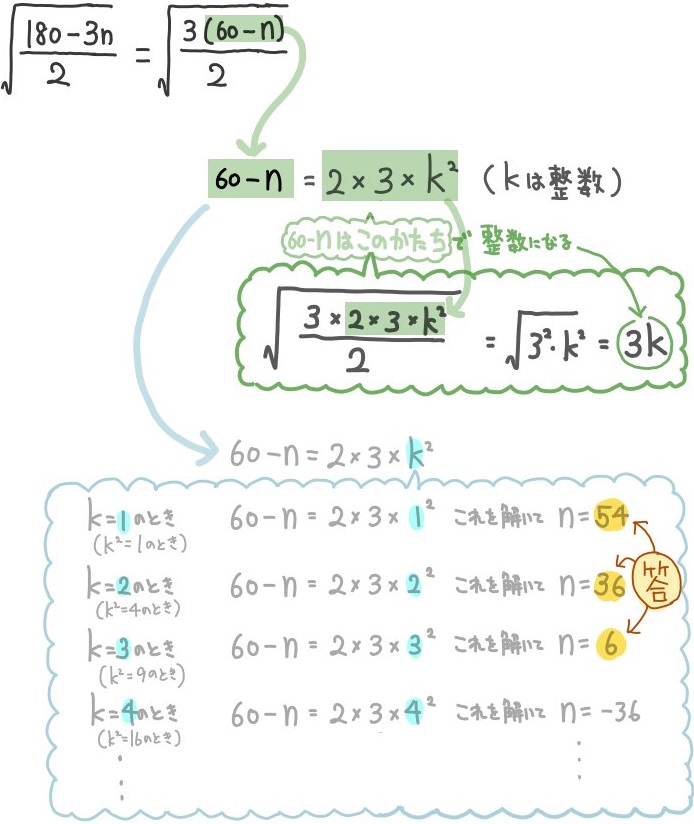
整数の２乗である\(k^{2}\) つまり平方数を絞り込んで、そこからｎを求めるという問題です。
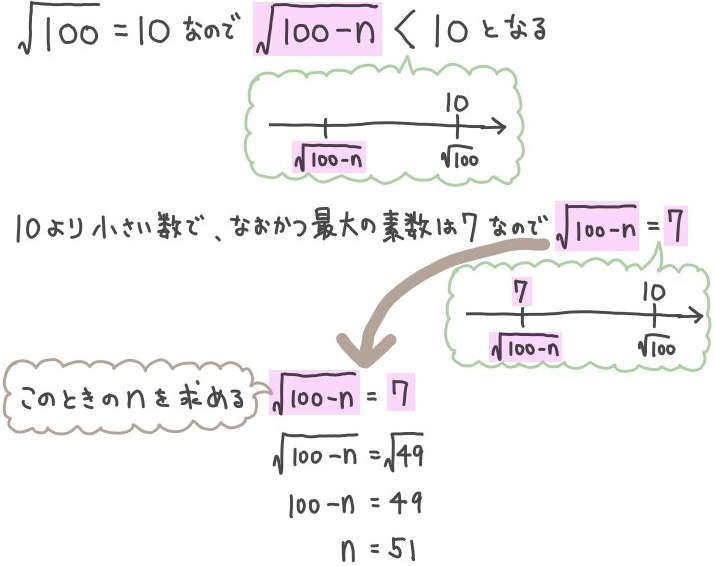このように平方根が素数となる問題であっても、範囲を検討して絞り込んでいけば難しくありません。
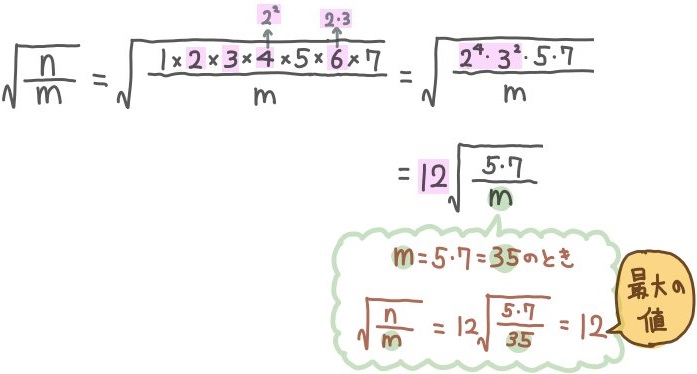ｍの値を答えるのではない、ということに注意してください。とりあえずnの値を素因数分解された形に整理して考えます。整理された形を眺めながら、ｍの値がどうであれば\(\sqrt{\dfrac{n}{m}}\) が整数となるかどうかについて考えます。
平方根の利用：奇数や偶数が登場する難問(難関私立対策)
- \(\sqrt{85-2n}\) が整数となる自然数ｎの値をすべて求めよ。
- \(\sqrt{80+n^{2}}\) が整数になるための自然数nをすべて求めよ。
- \(\sqrt{120+n^{2}}\) が整数になるための自然数nの個数を求めよ。
- \(\sqrt{18n}と\sqrt{6n+1}\) がともに整数となるような自然数nのうち最小の値を求めよ。
- \(\sqrt{\dfrac{80}{2\left( n+1\right) }}\)が偶数になるときの自然数ｎの値を求めよ。
- \(\sqrt{\dfrac{80}{2\left( n+1\right) }}\) が奇数になるときの自然数ｎの値を求めよ。
- \(\sqrt{\dfrac{180}{n}}\) が奇数になるときの自然数nの値をすべて求めよ。
- \(2\sqrt{\dfrac{1}{n}}\) が奇数になるときの自然数ｎの値を求めよ。
- \(30\sqrt{\dfrac{30}{3\left( n+1\right) }}\) が奇数になるときの自然数nの値をすべて求めよ。
- 自然数n、mが\(\sqrt{123+n}=m\sqrt{3}\) を満たすとき、最小のnの値を求めよ。
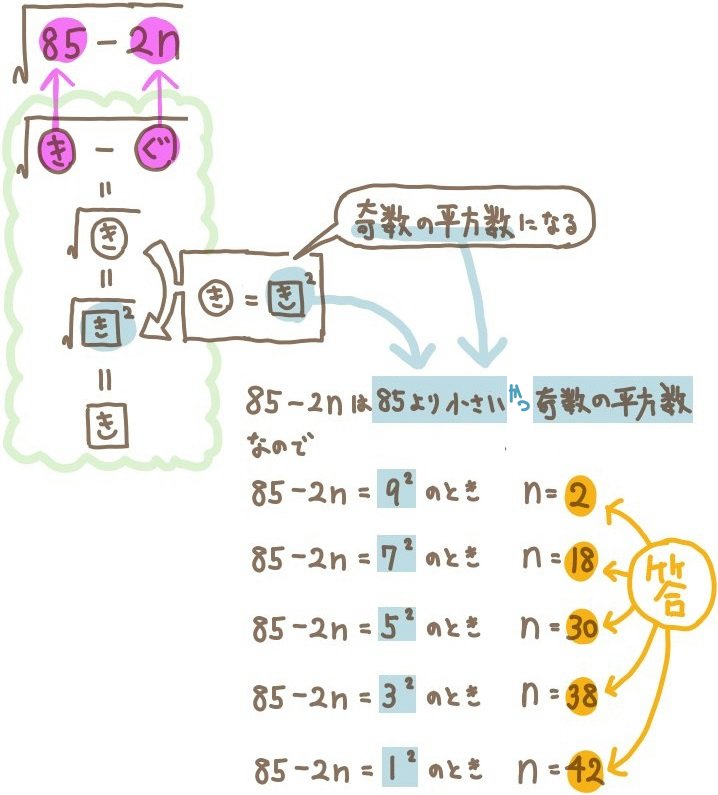平方根のなかの数が奇数引く偶数になっていますので、結果それは奇数ということになります。
平方根のなかの数が奇数で、平方根の記号が付いた数が整数となるとき、その整数は奇数ということになります。
つまり、平方根のなかの85-2n数は奇数の２乗のかたちになった奇数（奇数の平方数）になっているということです。（説明がややこしくてすみません）
また、85-2nは85より小さいので、奇数の平方数のなかで８５より小さい数ということになります。
奇数の平方数になる場合をそれぞれ調べて計算しているのが、上の説明図の最後の部分になります。
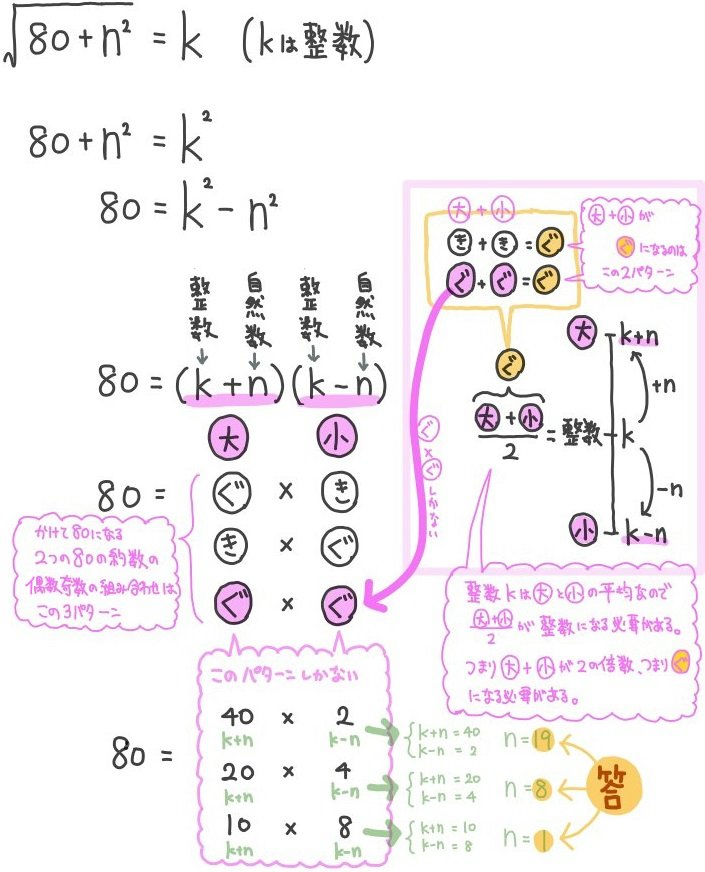
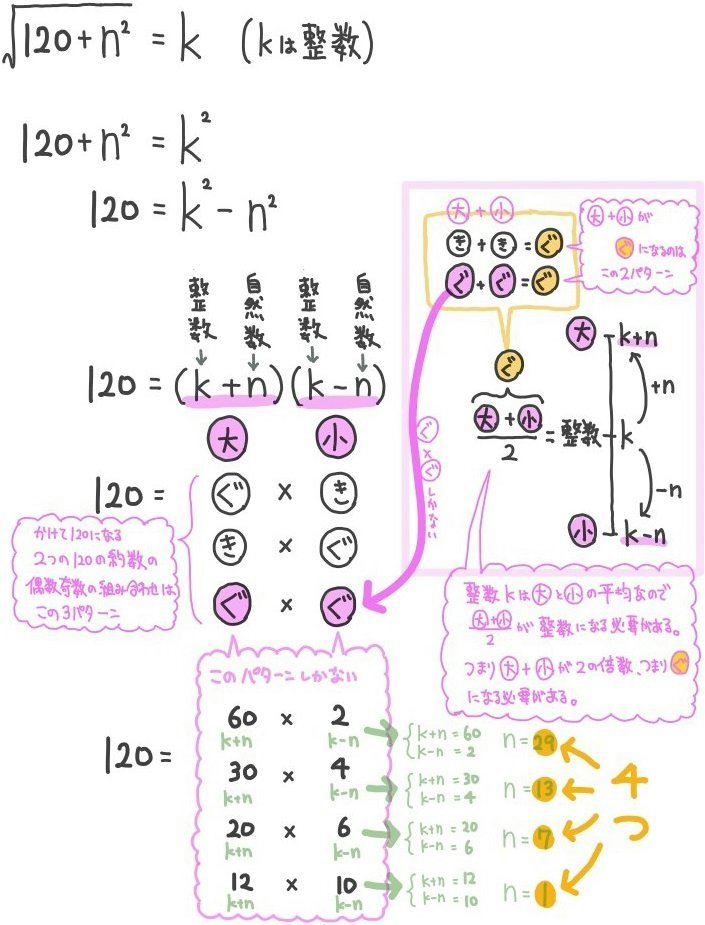
nの個数を求める問題なので、解答のみでよい場合は、ｎの値まで計算しきる必要はありません。
（秋田県）
nの候補は、平方根の記号が付いた式の値が奇数１になる場合のみしかありません。
もしも平方根の記号が付いた式の値が奇数３になる場合があるとしたら、平方根の記号のなかの素因数３が２個以上ある必要があります。
このあたりのことは少しわかりにくいかもしれないので、次の問題からより詳しく見ていきましょう。
\(2\sqrt{\dfrac{1}{n}}\)のかたちが２×平方根の数になっているので、平方根が整数になるときの自然数ｎを考えてしまってはいけないことになります。
このような場合は、図説のように、２を平方根のなかに入れてしまってから考えます。
\(\sqrt{\dfrac{4}{n}}\) が奇数１になるとき
以外の奇数の可能性も考える必要がありますが、この問題の場合は
\(\sqrt{\dfrac{4}{n}}\) が奇数１になるとき
しか自然数ｎの候補が存在しないことになります。
よってｎは４のみとなります。
これはかたちが複雑なようですが、先程の問題と同じ考え方で解けばそれほど難しくありません。
ただ、ルートの記号のついた値がどんな奇数になる場合があるかというところが難しいかもしれません。
特に奇数15になる場合を見過ごさないように注意すべき問題です。
おまけ：図形に関する平方根の利用の解き方と考え方
例えば、このような問題は平方根の記号に関する基本的な理解をつかわなければなりません。
一辺がxの正方形の面積が10のとき、xを求めよ。
このような問題の場合
２乗して１０になる自然数は何ですか？
と質問されているのと同じことになります。
よって答えはルート10ですね。
なので、正方形が図形問題に登場した場合や、解く過程で正方形を書き込んだ場合、平方根を利用する問題かも？という可能性に気が付けるといいですね。（もちろん、そうでない問題であるケースもありますが）