坂田先生
ここは、中学数学で学習する平方根の計算問題の難問を練習するページです。
にゃんこ
この問題&解答をプリントアウトしておきたい方は35問目の最後をご覧ください。（このテーマだけのドリル単品もあります）
このページの内容
- 平方根の計算問題｜中学数学の難問レベル
- 平方根の計算問題の難問｜高校入試の過去問編
広告
平方根の計算問題｜中学数学の難問レベル
(1) \(\dfrac{4+5\sqrt{2}}{\sqrt{2}}-\dfrac{2\sqrt{14}-\sqrt{7}}{\sqrt{7}}\)
(2) \({\small \left( \dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}+\dfrac{1}{\sqrt{6}}\right) \div \left( 1+\sqrt{2}+\sqrt{3}\right)} \)
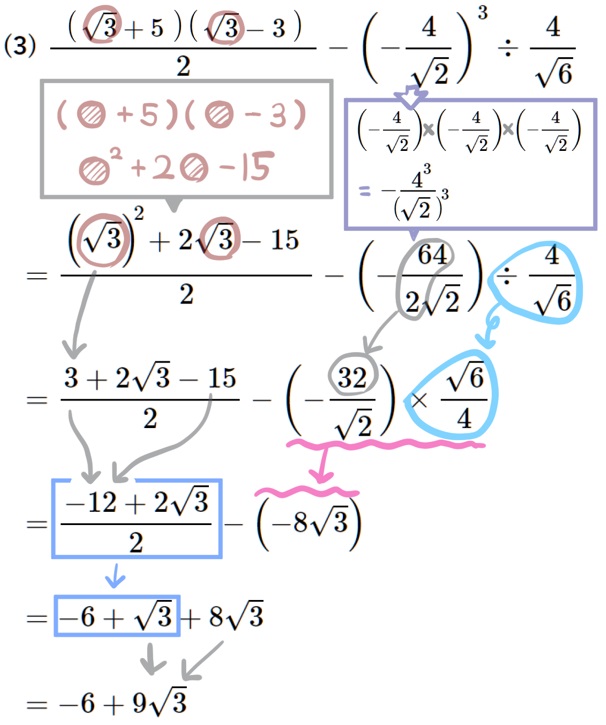
(3) \({\small \dfrac{\left( \sqrt{3}+5\right) \left( \sqrt{3}-3\right) }{2}-\left( -\dfrac{4}{\sqrt{2}}\right) ^{3}\div \dfrac{4}{\sqrt{6}}}\)
(4) \({\small \sqrt{5}\left( \dfrac{1}{\sqrt{10}}-\dfrac{2}{\sqrt{5}}\right) -\sqrt{5}\left( \dfrac{1}{\sqrt{10}}+\dfrac{2}{\sqrt{5}}\right)} \)
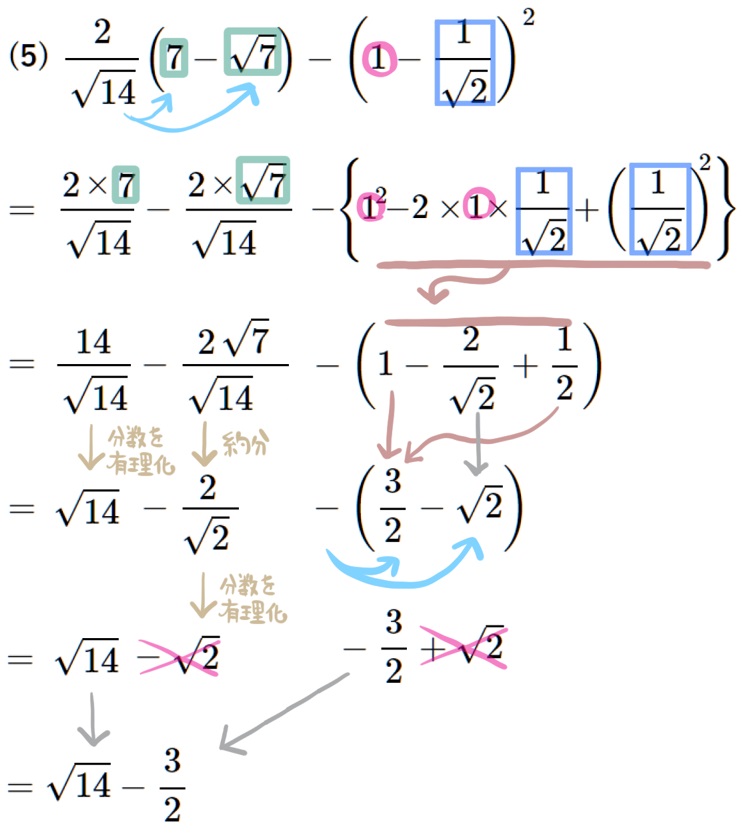
(5) \(\dfrac{2}{\sqrt{14}}\left( 7-\sqrt{7}\right) -\left( 1-\dfrac{1}{\sqrt{2}}\right) ^{2}\)
(6) \(\dfrac{2\sqrt{2}-\sqrt{6}}{\sqrt{3}}-\dfrac{1+\sqrt{3}}{\sqrt{2}}\)
(7) \(\dfrac{1}{\sqrt{2}+\sqrt{3}}-\dfrac{1}{\sqrt{3}-\sqrt{2}}\)
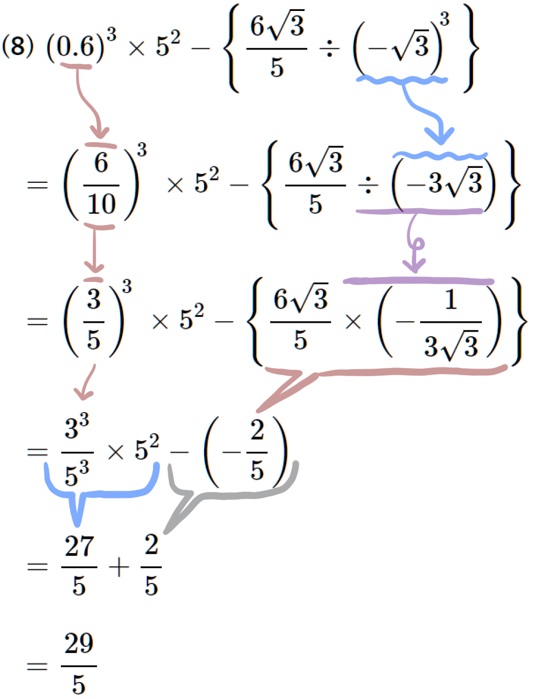
(8) \(\left( 0.6\right) ^{3}\times 5^{2}-\left\{ \dfrac{6\sqrt{3}}{5}\div \left( -\sqrt{3}\right) ^{3}\right\} \)
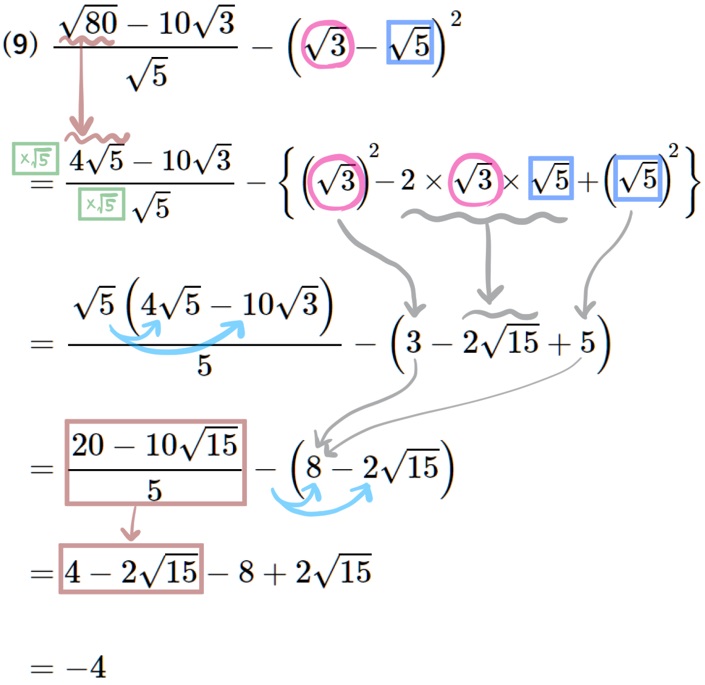
(9) \(\dfrac{\sqrt{80}-10\sqrt{3}}{\sqrt{5}}-\left( \sqrt{3}-\sqrt{5}\right) ^{2}\)
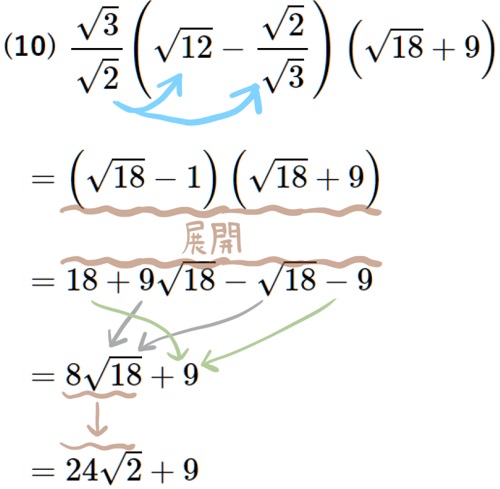
(10) \(\dfrac{\sqrt{3}}{\sqrt{2}}\left( \sqrt{12}-\dfrac{\sqrt{2}}{\sqrt{3}}\right) \left( \sqrt{18}+9\right) \)
(11) \(\dfrac{\sqrt{7}\left( \sqrt{21}+1\right) }{7}-\dfrac{1+\sqrt{28}}{\sqrt{7}}+2\)
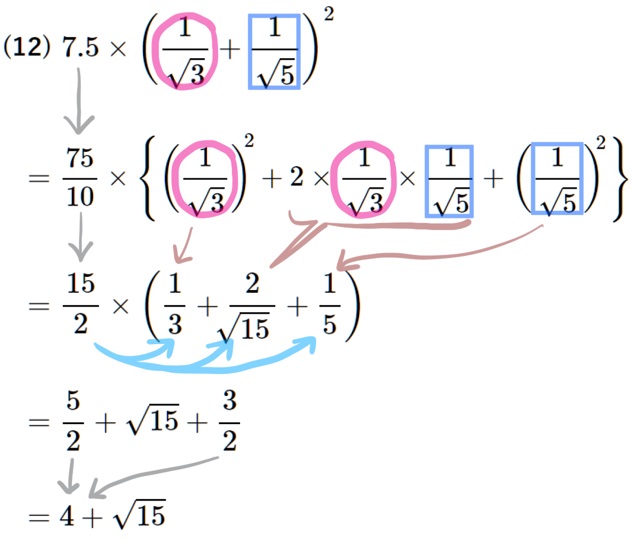
(12) \(7.5\times \left( \dfrac{1}{\sqrt{3}}+\dfrac{1}{\sqrt{5}}\right) ^{2}\)
(13) \({\small -\dfrac{7}{\sqrt{10}}\left\{ \dfrac{\left( \sqrt{5}+1\right) ^{2}}{\sqrt{2}}+\left( -\sqrt{2}\right) ^{3}-\sqrt{2}\right\} }\)
(14) \(\dfrac{\left( 3\sqrt{2}-\sqrt{6}\right) \left( \sqrt{3}+3\right) }{\sqrt{2}}-\dfrac{1}{2}\)
(15) \({\small \left( \sqrt{7}+1\right) ^{3}\left( \sqrt{7}-1\right) -\left( \sqrt{7}+1\right) \left( \sqrt{7}-1\right) ^{3}}\)
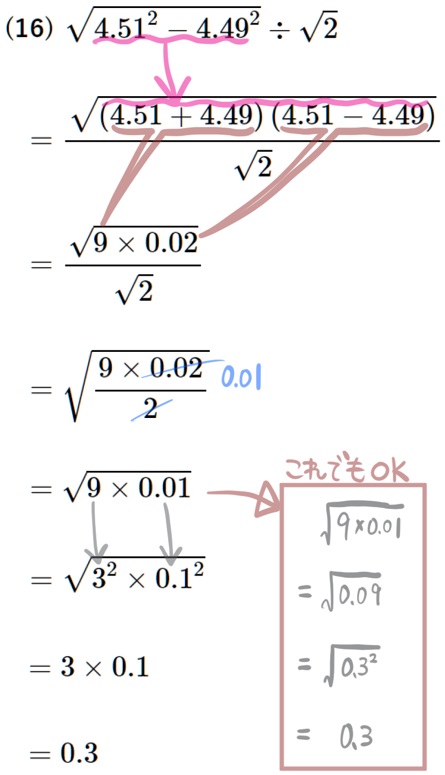
(16) \(\sqrt{4.51^{2}-4.49^{2}}\div \sqrt{2}\)
(17) \({\small \dfrac{1}{\sqrt{5}}\left\{ \left( \sqrt{5}+2\sqrt{2}\right) ^{2}-\left( 2\sqrt{5}+\sqrt{2}\right) ^{2}\right\} -\dfrac{1}{\sqrt{5}}}\)
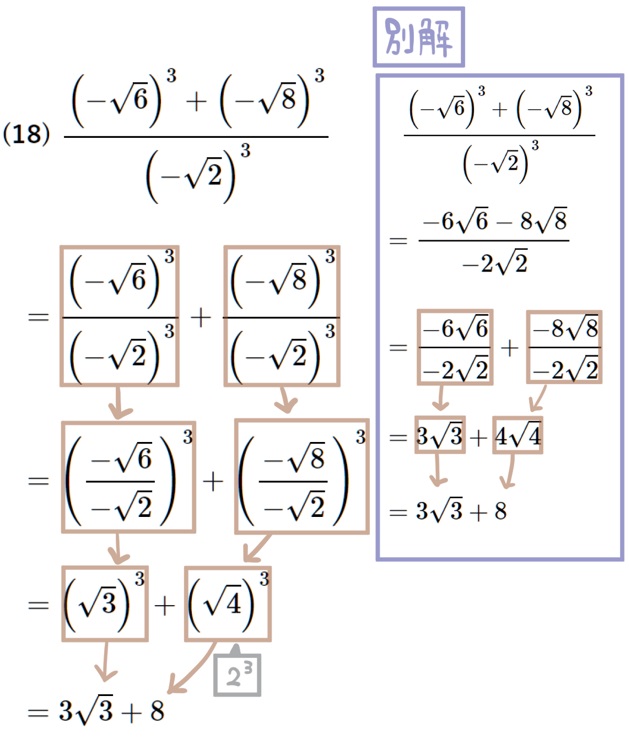
(18) \(\dfrac{\left( -\sqrt{6}\right) ^{3}+\left( -\sqrt{8}\right) ^{3}}{\left( -\sqrt{2}\right) ^{3}}\)
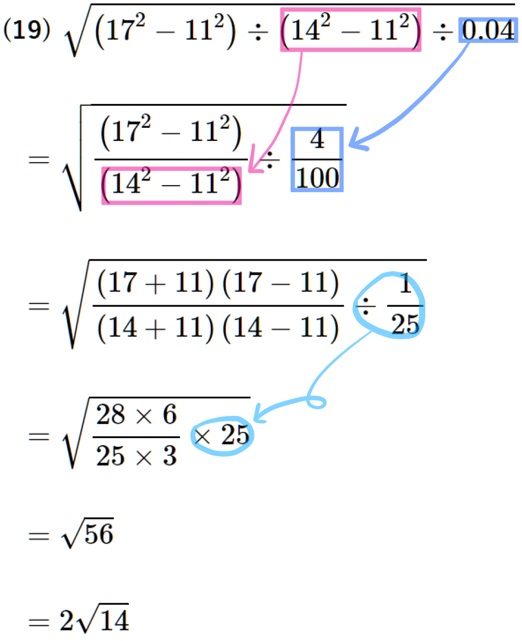
(19) \(\sqrt{\left( 17^{2}-11^{2}\right) \div \left( 14^{2}-11^{2}\right) \div 0.04}\)
(20) \({\tiny \left( \dfrac{\sqrt{3}+1}{\sqrt{2}}\right) ^{2}+2\left( \dfrac{\sqrt{3}+1}{\sqrt{2}}\right) \left( \dfrac{\sqrt{3}-1}{\sqrt{2}}\right) +\left( \dfrac{\sqrt{3}-1}{\sqrt{2}}\right) ^{2}}\)
(21) \({\small \left( 2-\dfrac{1}{\sqrt{2}}\right) ^{2}-\dfrac{\left( \sqrt{6}-\sqrt{3}\right) \left( -1+\sqrt{2}\right) }{\sqrt{3}}}\)
(22) \(\dfrac{1}{1-\sqrt{2}-\sqrt{3}}-\dfrac{1}{1-\sqrt{2}+\sqrt{3}}\)
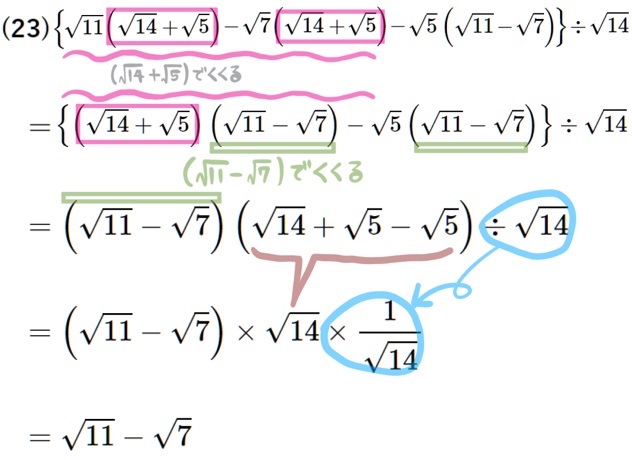
(23) \({\tiny \left\{ \sqrt{11}\left( \sqrt{14}+\sqrt{5}\right) -\sqrt{7}\left( \sqrt{14}+\sqrt{5}\right) -\sqrt{5}\left( \sqrt{11}-\sqrt{7}\right) \right\} \div \sqrt{14}}\)
(24) \(\left\{ \left( 2\sqrt{3}+\sqrt{11}\right) ^{2}\left( \sqrt{11}-\sqrt{12}\right) ^{2}\right\} ^{3}\)
(25) \(\dfrac{\left( \sqrt{3}+\sqrt{2}\right) ^{5}\left( \sqrt{3}-\sqrt{2}\right) ^{6}}{\left( \sqrt{7}+\sqrt{6}\right) ^{5}\left( \sqrt{7}-\sqrt{6}\right) ^{5}}\)
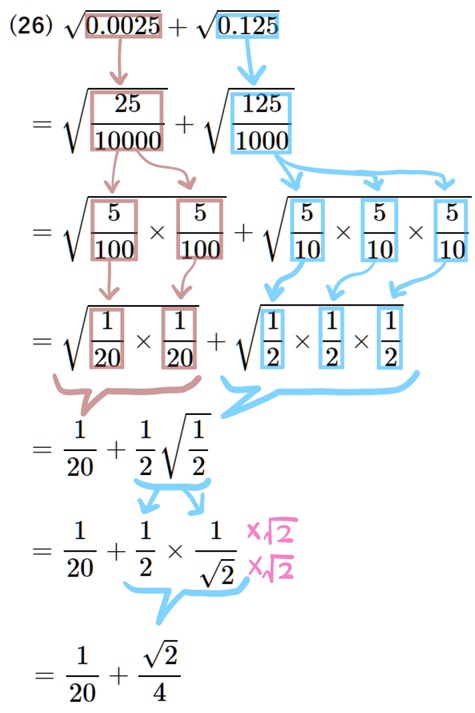
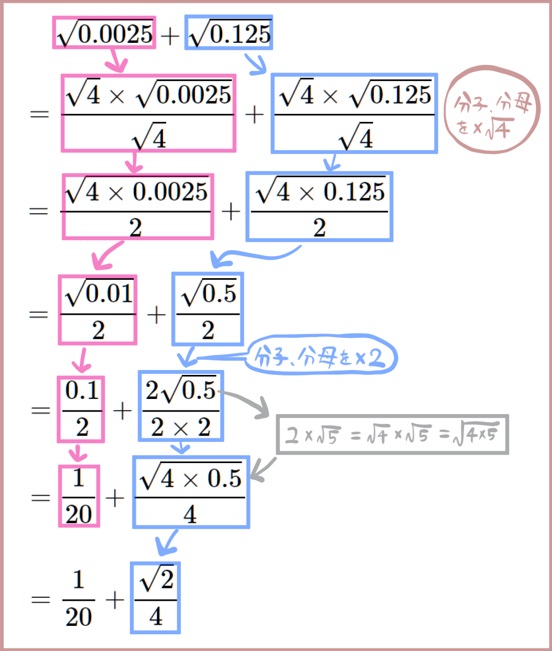
(26) \(\sqrt{0.0025}+\sqrt{0.125}\)
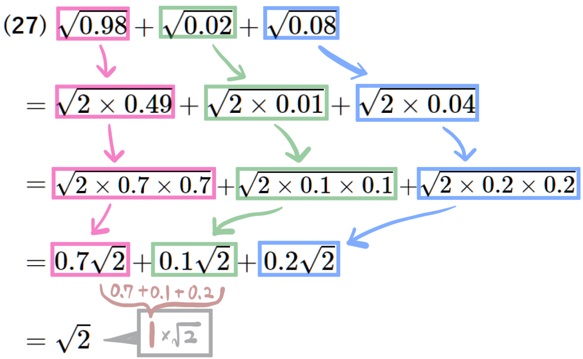
(27) \(\sqrt{0.98}+\sqrt{0.02}+\sqrt{0.08}\)
(28) \({\tiny \left\{ \left( 7+4\sqrt{3}\right) ^{3}+\left( 7-4\sqrt{3}\right) ^{3}\right\} ^{2}-\left\{ \left( 7+4\sqrt{3}\right) ^{3}-\left( 7-4\sqrt{3}\right) ^{3}\right\} ^{2}}\)
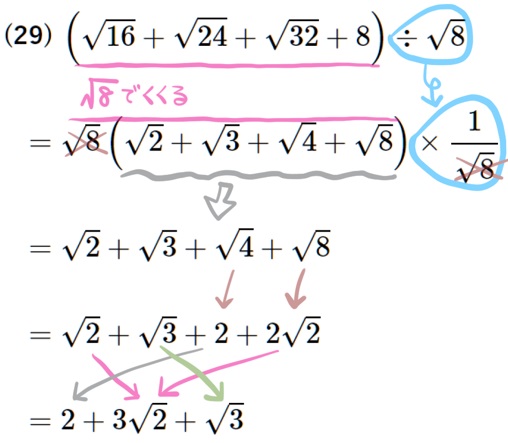
(29) \(\left( \sqrt{16}+\sqrt{24}+\sqrt{32}+8\right) \div \sqrt{8}\)
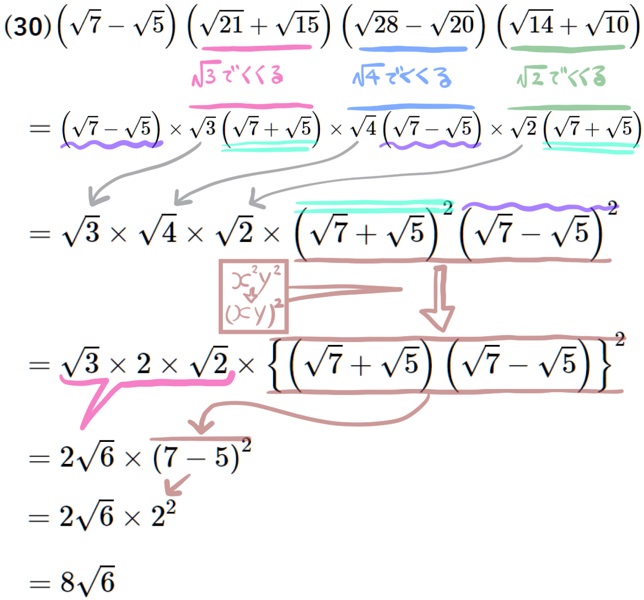
(30) \({\tiny \left( \sqrt{7}-\sqrt{5}\right) \left( \sqrt{21}+\sqrt{15}\right) \left( \sqrt{28}-\sqrt{20}\right) \left( \sqrt{14}+\sqrt{10}\right)} \)
(31) \({\tiny \left( 1-\sqrt{2}+\sqrt{3}-\sqrt{5}\right) ^{2}+\left( 1+\sqrt{2}-\sqrt{3}-\sqrt{5}\right) ^{2}}\)
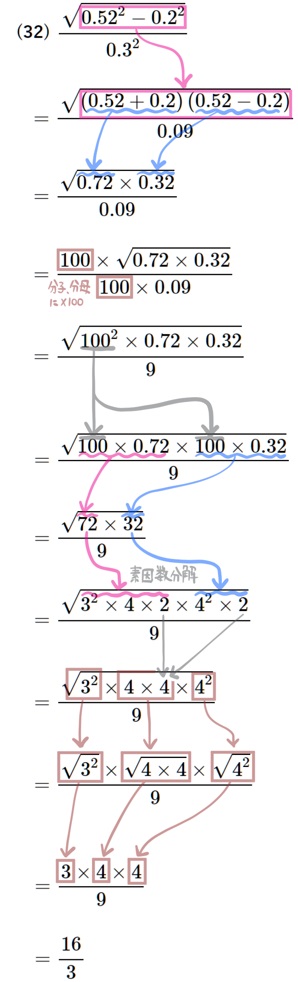
(32) \(\dfrac{\sqrt{0.52^{2}-0.2^{2}}}{0.3^{2}}\)
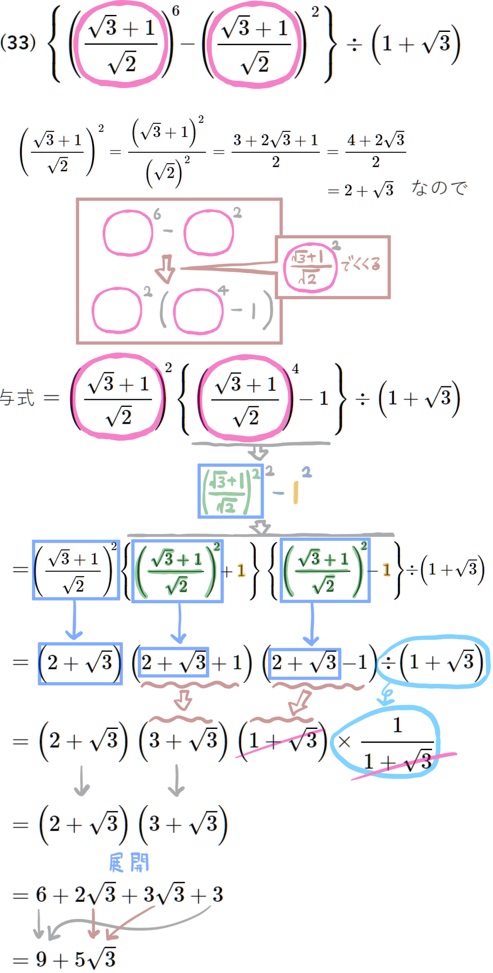
(33) \({\small \left\{ \left( \dfrac{\sqrt{3}+1}{\sqrt{2}}\right) ^{6}-\left( \dfrac{\sqrt{3}+1}{\sqrt{2}}\right) ^{2}\right\} \div \left( 1+\sqrt{3}\right)} \)
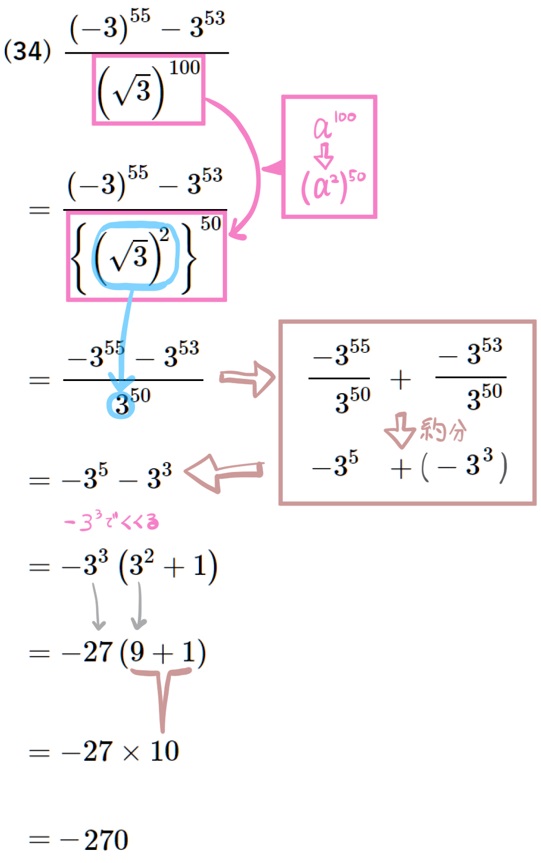
(34) \(\dfrac{\left( -3\right) ^{55}-3^{53}}{\left( \sqrt{3}\right) ^{100}}\)
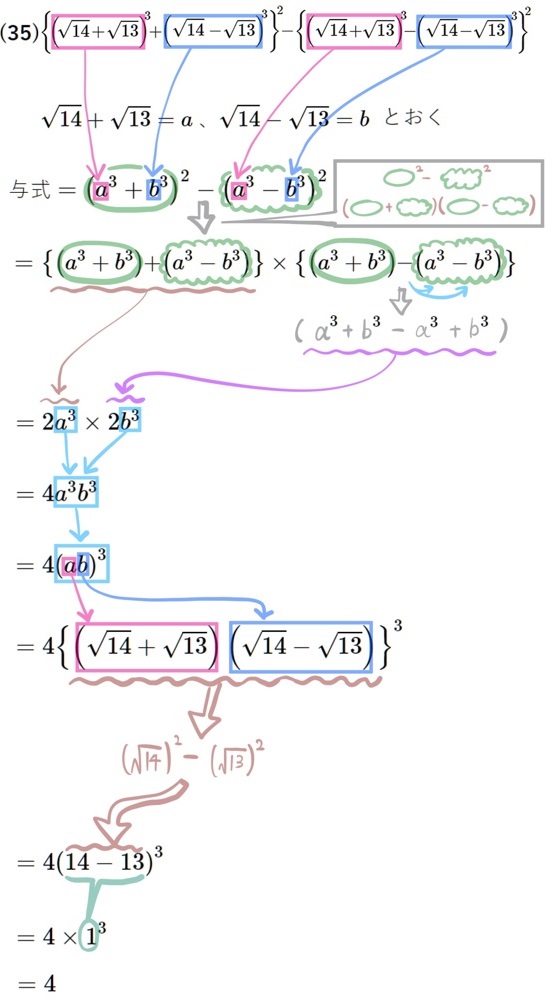
(35) \({\tiny \left\{ \left( \sqrt{14}+\sqrt{13}\right) ^{3}+\left( \sqrt{14}-\sqrt{13}\right) ^{3}\right\} ^{2}-\left\{ \left( \sqrt{14}+\sqrt{13}\right) ^{3}-\left( \sqrt{14}-\sqrt{13}\right) ^{3}\right\} ^{2}}\)
にゃんこ
この35問をプリントアウトして学習したい方はこちら
※セット版も単品版もあります。
にゃんこ
にゃんこ
坂田先生
広告
にゃんこ
広告
平方根の計算問題の難問｜高校入試の過去問編
指数に着目する平方根の計算問題
計算しなさい。(市川高校)
\(\left( \sqrt{7}+\sqrt{5}\right) ^{2}\left( \sqrt{7}-\sqrt{5}\right) ^{2}\)
\(+\left( \sqrt{3}+\sqrt{2}\right) ^{2}\left( \sqrt{3}-\sqrt{2}\right) ^{2}\)
～アドバイス～
ここでの解説がわかりにくいという場合は、指数の取り扱いについて復習しておくといいでしょう。
分数に平方根がある計算問題1
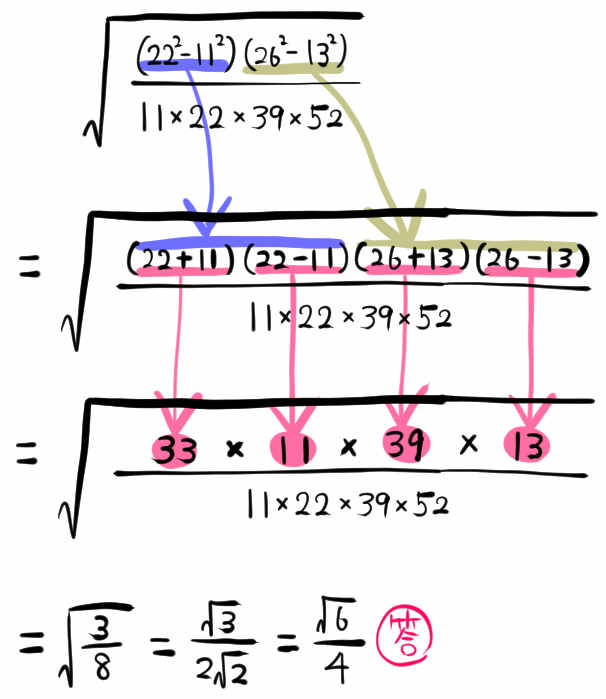
\(\sqrt{\dfrac{\left( 22^{2}-11^{2}\right) \left( 26^{2}-13^{2}\right) }{11\times 22\times 39\times 52}}\)
を計算しなさい。(青山学院高校)
～解き方のポイント～
この問題はとりあえず平方根を気にしないで、その中にある分数式の部分にまず集中しましょう。
分数に平方根がある計算問題2
\(\dfrac{\sqrt{1.52^{2}-1.48^{2}}}{\sqrt{2.29^{2}-2.21^{2}}}\)
を計算しなさい。(立命館高校)
これでも前の問題と同様、平方根を気にしないで中の計算を工夫してゆくパターンです。ただ、分母と分子の平方根を一緒にしてから考える、というステップが追加されています。
展開しないで処理する
\(\sqrt{12}\left( \sqrt{13}+\sqrt{68}\right) \)
\(+\sqrt{34}\left( \sqrt{13}+\sqrt{68}\right) \)
\(-\sqrt{13}\left( \sqrt{12}+\sqrt{34}\right) \)
\(-\sqrt{24}\left( \sqrt{12}+\sqrt{34}\right) \)
を計算しなさい。(慶應義塾女子高校)
展開しないで共通因数を見つけて簡単なかたちに変形し、処理してゆくパターンです。
そのまま計算しない工夫
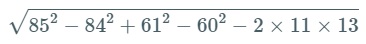
を計算しなさい。(慶應義塾女子高校)
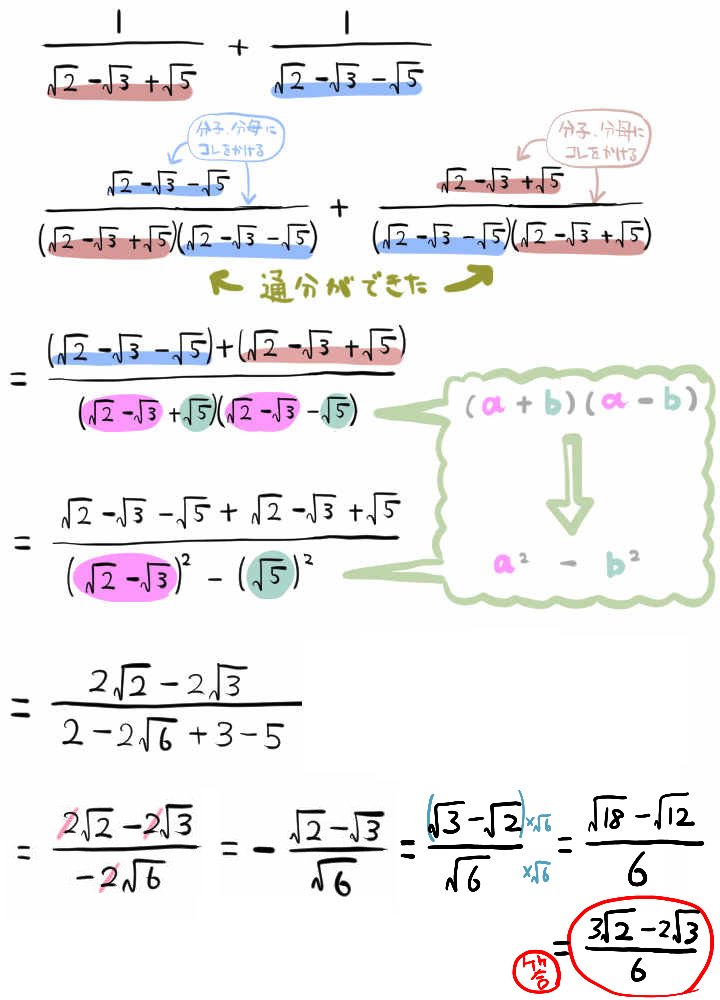
平方根の式を通分する計算問題
\(\dfrac{1}{\sqrt{2}-\sqrt{3}+\sqrt{5}}+\dfrac{1}{\sqrt{2}-\sqrt{3}-\sqrt{5}}\)
を計算しなさい。(東大寺学園高校)
分母に平方根の式がある場合の通分について練習できる問題です。慣れない場合は手を動かしてスラスラ解ける状態に仕上げておきましょう。
同じ式は文字で処理せよ1
\(\left\{ \left( 3+2\sqrt{2}\right) ^{4}+\left( 3-2\sqrt{2}\right) ^{4}\right\} ^{2}\)
\(-\left\{ \left( 3+2\sqrt{2}\right) ^{4}-\left( 3-2\sqrt{2}\right) ^{4}\right\} ^{2}\)
を計算しなさい。(巣鴨高校)
～解き方のポイント～
４乗の式をどう処理するかと考える前に、まず平方根の式で同じものがあるので、それを文字で置き変えて計算してみましょう。すると、きれいに処理できてしまうというパターンです。
同じ式は文字で処理せよ2
\(\left( \sqrt{7}-\sqrt{5}\right) ^{8}\left( \sqrt{7}+\sqrt{5}\right) ^{10}\)
\(-\left( \sqrt{7}-\sqrt{5}\right) ^{10}\left( \sqrt{7}+\sqrt{5}\right) ^{8}\)
を計算しなさい。(早稲田実業高校)
指数が大きい場合でも、先程の問題と同じパターンです。ただ、どこまでの式を文字に置き換えるかという点が少し違います。
何を文字に置き換えるか？
\(\left( \sqrt{2}+1\right) ^{4}-\left( \sqrt{2}-1\right) ^{4}\)
を計算しなさい。(慶應義塾高校)
指数法則と平方根の計算問題
\(\dfrac{\left\{ \left( 1+\sqrt{3}\right) ^{50}\right\} ^{2}\left( 2-\sqrt{3}\right) ^{50}}{2^{50}}\)
を計算しなさい。(立命館高校)
指数法則を使った処理について慣れていない場合は難問に見える問題です。また、解説のように一部だけを取り出して計算しないと、手間が膨大になってしまいます。
平方根の因数でくくり出す計算問題
\(\left( \sqrt{77}+7\right) \left( \sqrt{44}-\sqrt{28}-\dfrac{8}{\sqrt{11}}\right)\)
を計算しなさい。(開成高校)
これが難問の理由は、7の処理の仕方にあります。このような計算問題の経験がないと気が付きにくいでしょう。
にゃんこ
これ以外にも『平方根の取り扱いを学習できる入試問題のテーマ』がありますので、必要な方は練習しておいてください。
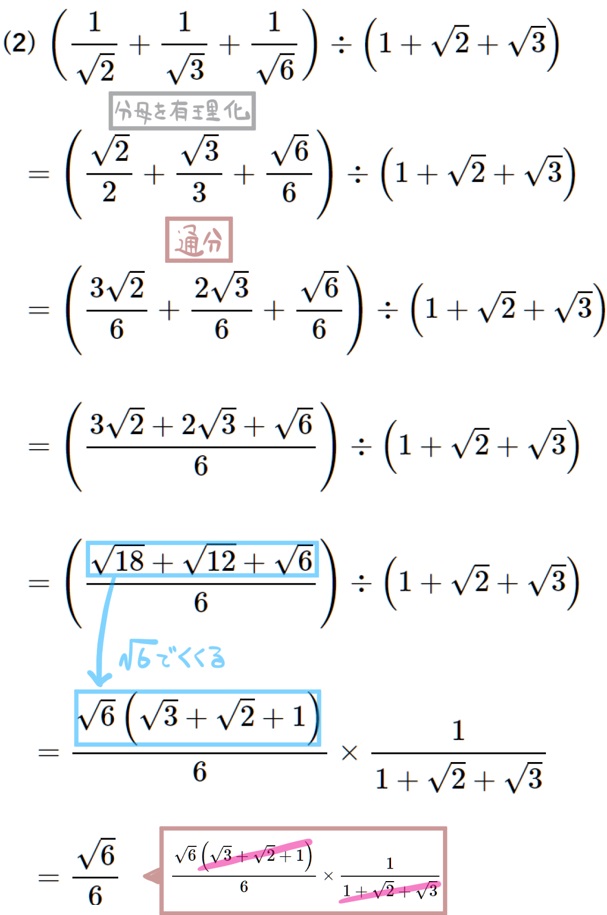
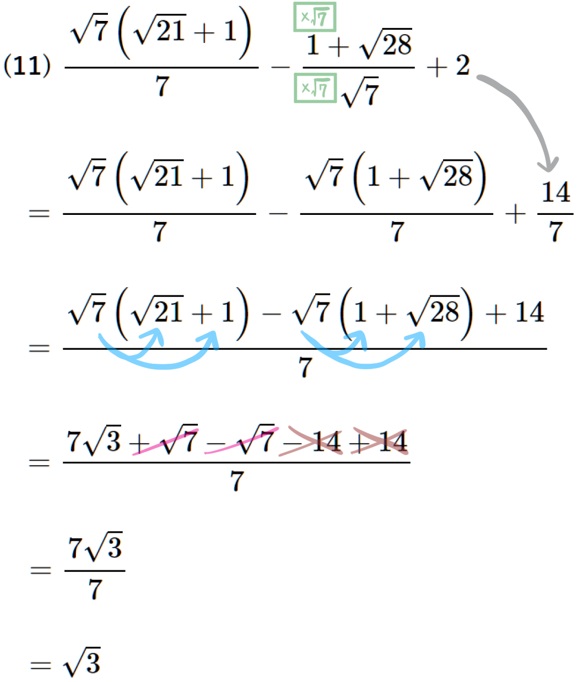
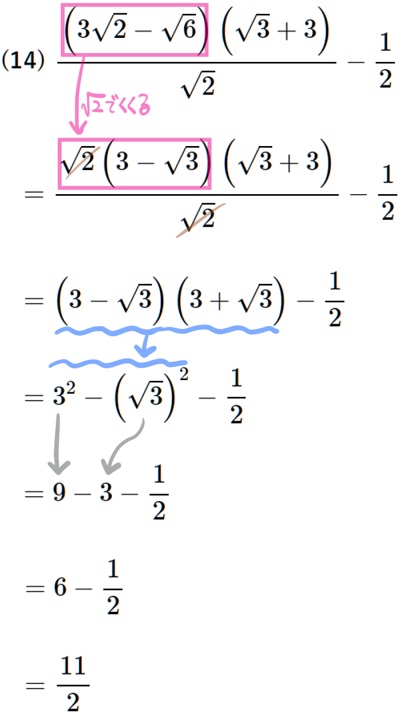
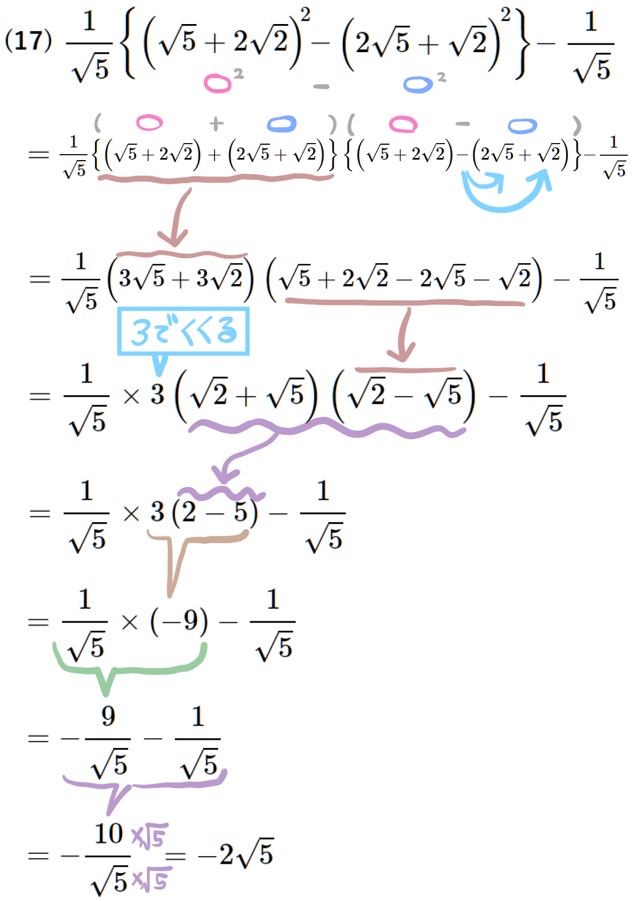
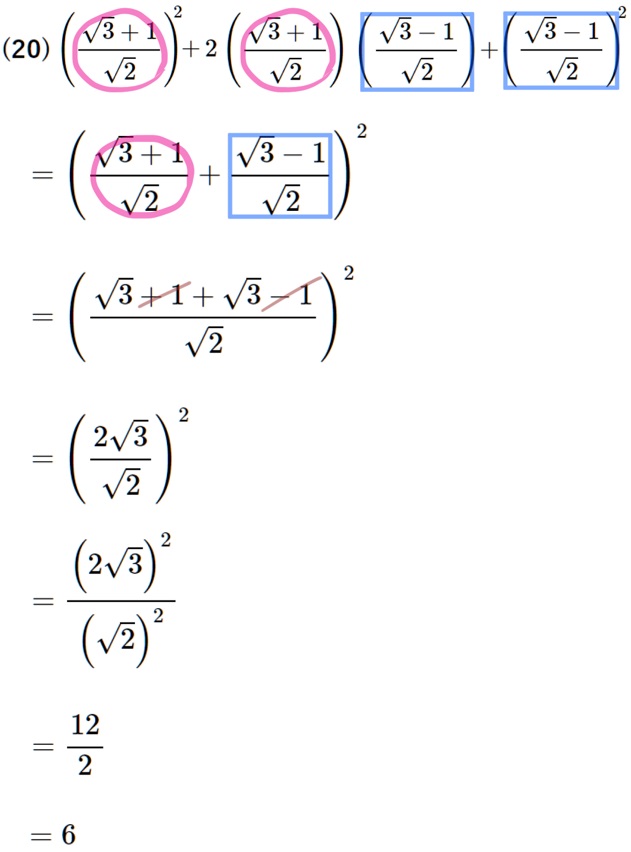
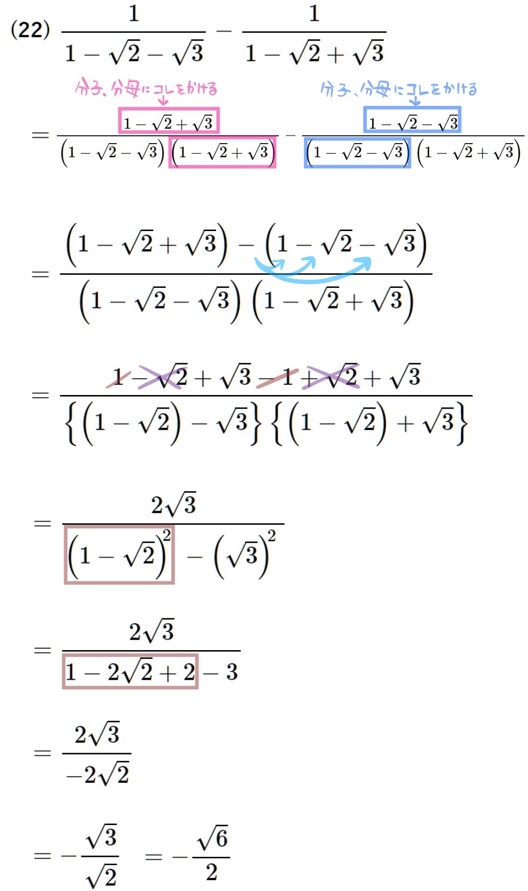
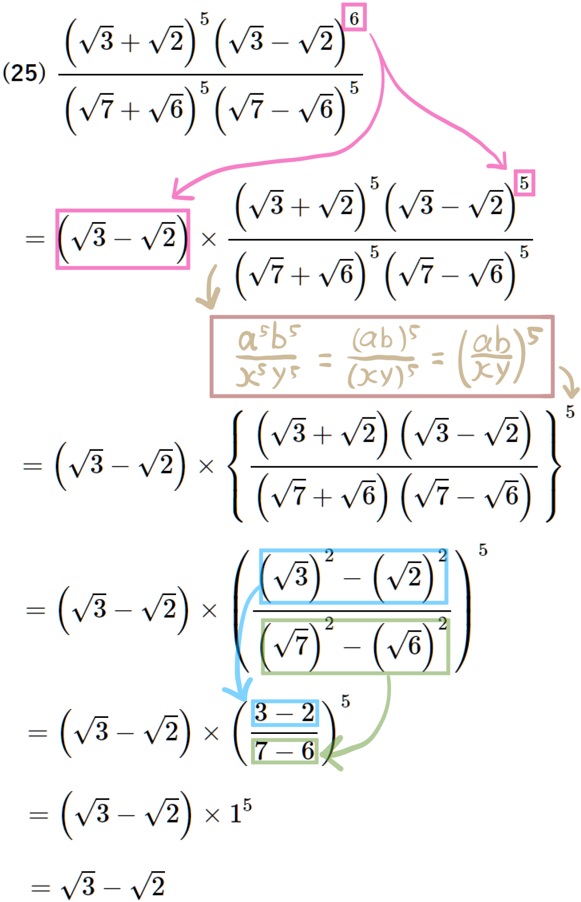
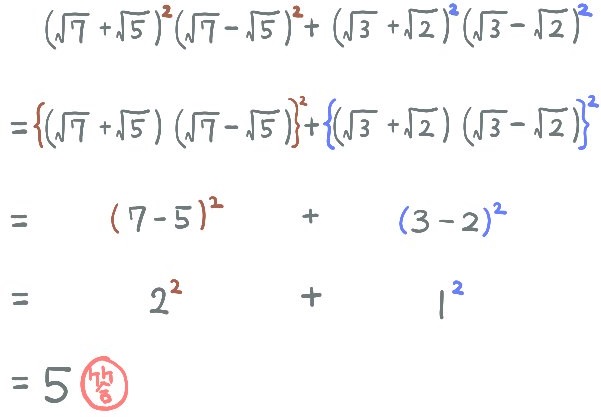
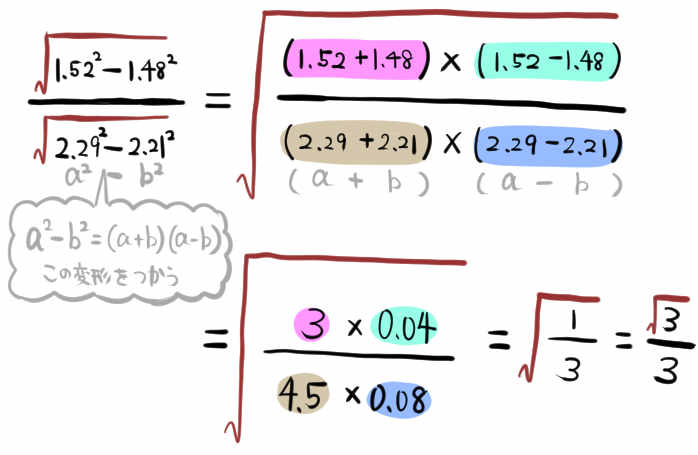
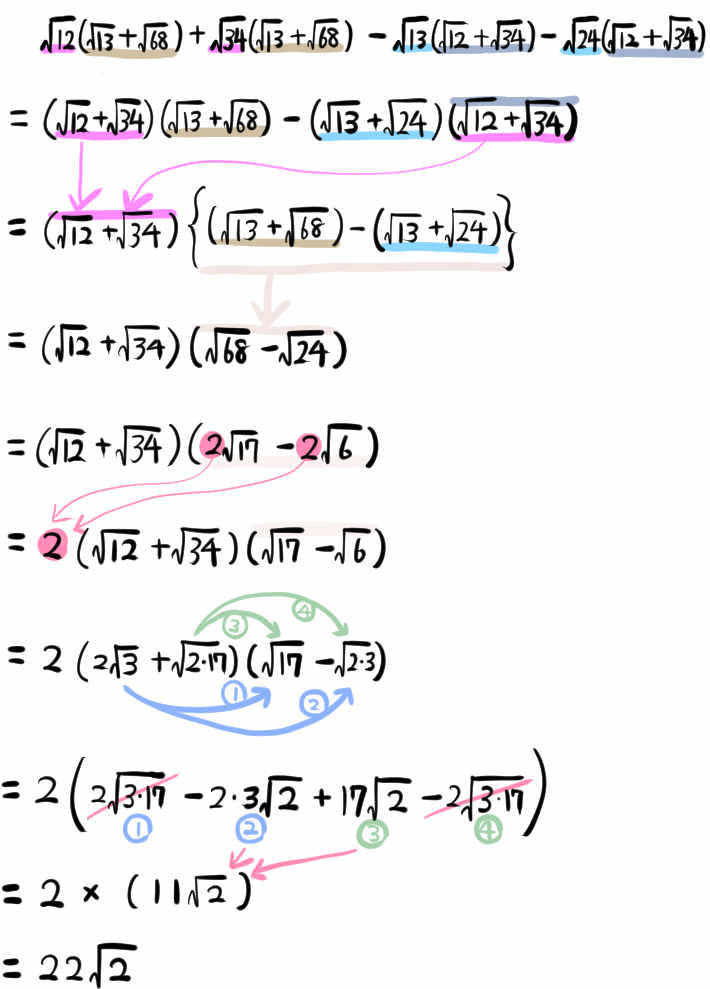
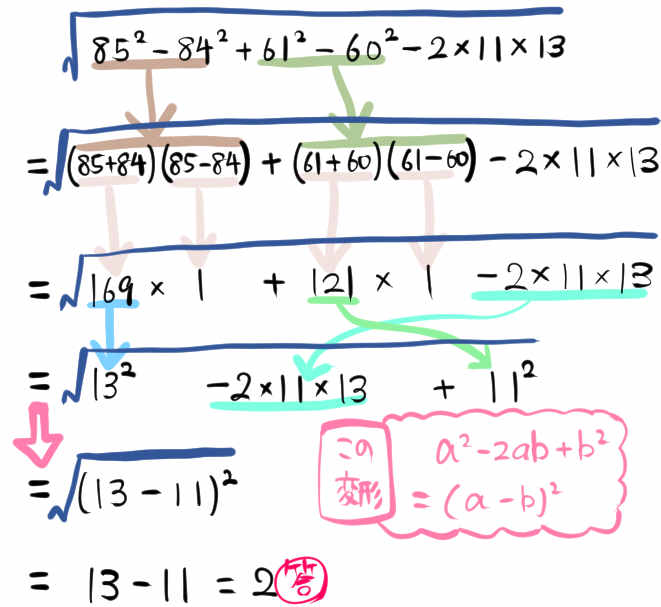
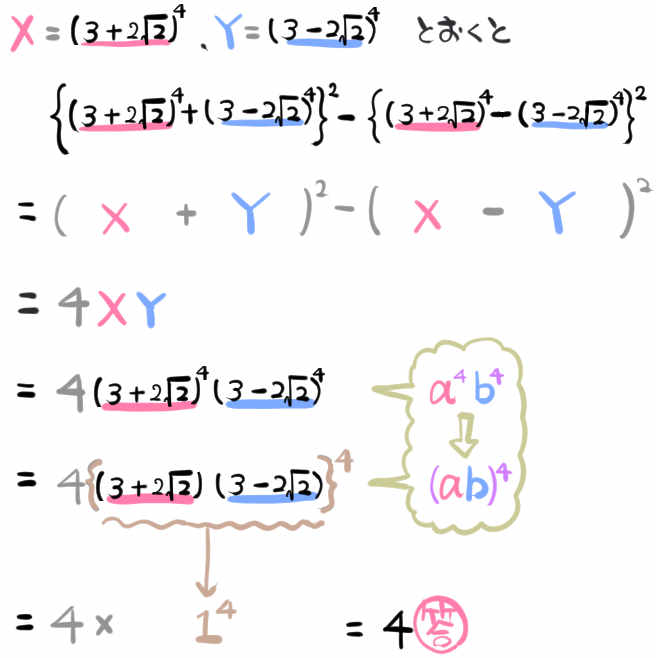
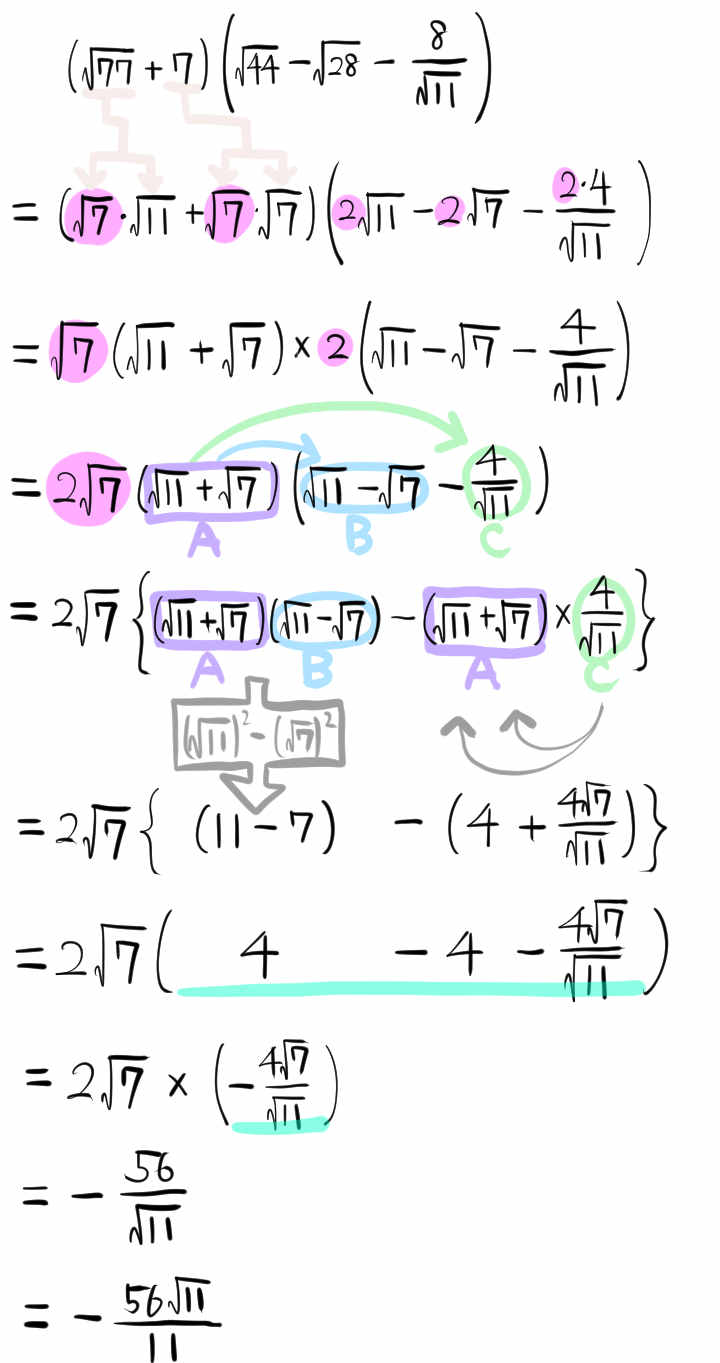7をルート7とルート7に因数分解して計算の工夫をしてゆく処理が、初見の場合は難しいでしょう。
