


平方根の大小関係と大小比較の練習問題|中学数学
- \(-\sqrt{2}\) 、 \(-\sqrt{5}\) 、\(-\sqrt{7}\) の大小関係を不等号で表せ。
- \(a<b<c\) のとき \(-\sqrt{a}\) 、 \(-\sqrt{b}\) 、\(-\sqrt{c}\) の大小関係を不等号で表せ。
- \(\dfrac{7}{2} < \sqrt{n} <4\) となるような自然数nの個数を求めよ。
- \(\dfrac{7}{2}\leqq \sqrt{n}\leqq 4\) となるような自然数nの個数を求めよ。
- \(\sqrt{15} <n <2\sqrt{10}\) となるような自然数nの個数を求めよ。
- \(-3\sqrt{3}\) より大きく、 \(2\sqrt{5}\) より小さい整数は何個あるか。
- \(\dfrac{6}{\sqrt{3}}\) 、 \(\dfrac{5}{\sqrt{2}}\) 、 \(3.5\) の大小関係を不等号で表せ。
- \(-5\) 、 \(-3\sqrt{3}\) 、 \(-\dfrac{\sqrt{104}}{2}\) の大小関係を不等号で表せ。
- \(9.9 ≦\sqrt{n+0.01} <10.1\) となるような自然数nをすべて求めよ。

 ルートの中の値の大小関係は、-の符号が付いた場合、大小関係が逆転します。
ルートの中の値の大小関係は、-の符号が付いた場合、大小関係が逆転します。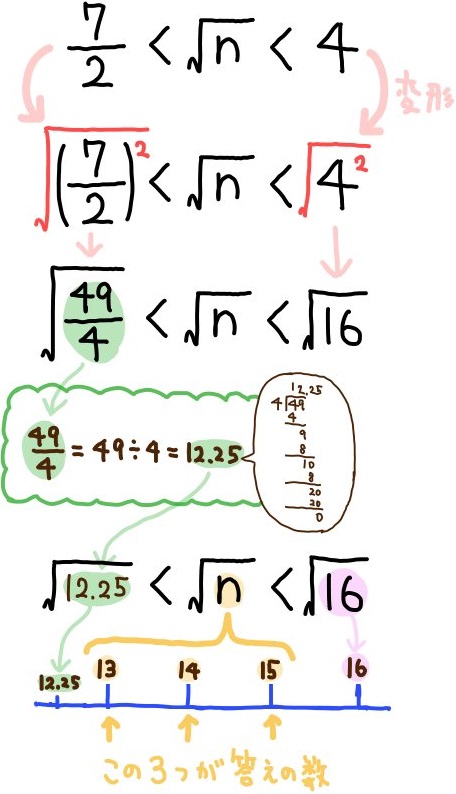 不等号で表された平方根の大小関係をヒントに自然数nの個数を求める問題です。
不等号で表された平方根の大小関係をヒントに自然数nの個数を求める問題です。
このタイプの問題で難しいポイントは、不等号の指し示す範囲がどこまでのものかをちゃんと把握しなければミスをしてしまうという所です。



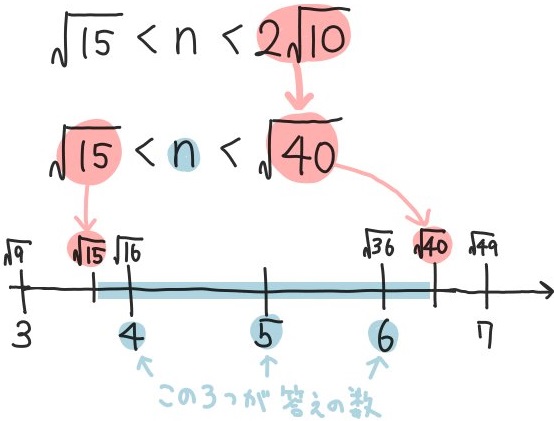 これもまた数直線を使って、自然数nの範囲を特定してから検討する問題です。中学数学の定期テストでも十分出題される『平方根の大小関係の問題』です。
これもまた数直線を使って、自然数nの範囲を特定してから検討する問題です。中学数学の定期テストでも十分出題される『平方根の大小関係の問題』です。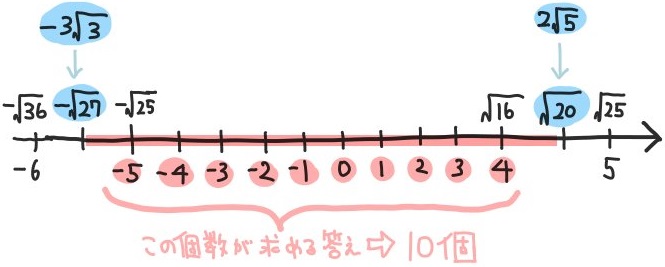 これもまた、先程と同じタイプの平方根の問題です。しかし不等号による式ではなく、文章で表現されています。
これもまた、先程と同じタイプの平方根の問題です。しかし不等号による式ではなく、文章で表現されています。
「より」という表現はその数値自身を含まない、という点に注意してください。
 中学数学や高校入試数学の平方根の問題において、大小関係を調べる場合は、すべて平方根の記号で表現したものに変換し、それから比較するという方法が基本です。
中学数学や高校入試数学の平方根の問題において、大小関係を調べる場合は、すべて平方根の記号で表現したものに変換し、それから比較するという方法が基本です。
この問題ではその際、平方根の分母の有理化を使用する場合と、しない場合の両方の変形を紹介しています。

\(5=\sqrt{25}\)
\(3\sqrt{3}=\sqrt{27}\)
\(\dfrac{\sqrt{104}}{2}=\dfrac{\sqrt{104}}{\sqrt{4}}=\sqrt{26}\)
\(25<26<27\) なので
\(\sqrt{25}<\sqrt{26}<\sqrt{27}\)
したがって
\(5<\dfrac{\sqrt{104}}{2}<3\sqrt{3}\)


\(-3\sqrt{3}<-\dfrac{\sqrt{104}}{2}<-5\)

平方根の大小関係と大小比較の難問|高校入試の応用問題
- \(\sqrt{20}\leqq \sqrt{x^{2}}\leqq 10\) を満たす整数xの個数を求めよ。
- \(5\sqrt{2}\) 、\(7\) 、\(\dfrac{\sqrt{192}}{2}\) 、 \(\sqrt{3}+\sqrt{27}-\sqrt{2}\) の大小関係を不等号で表せ。
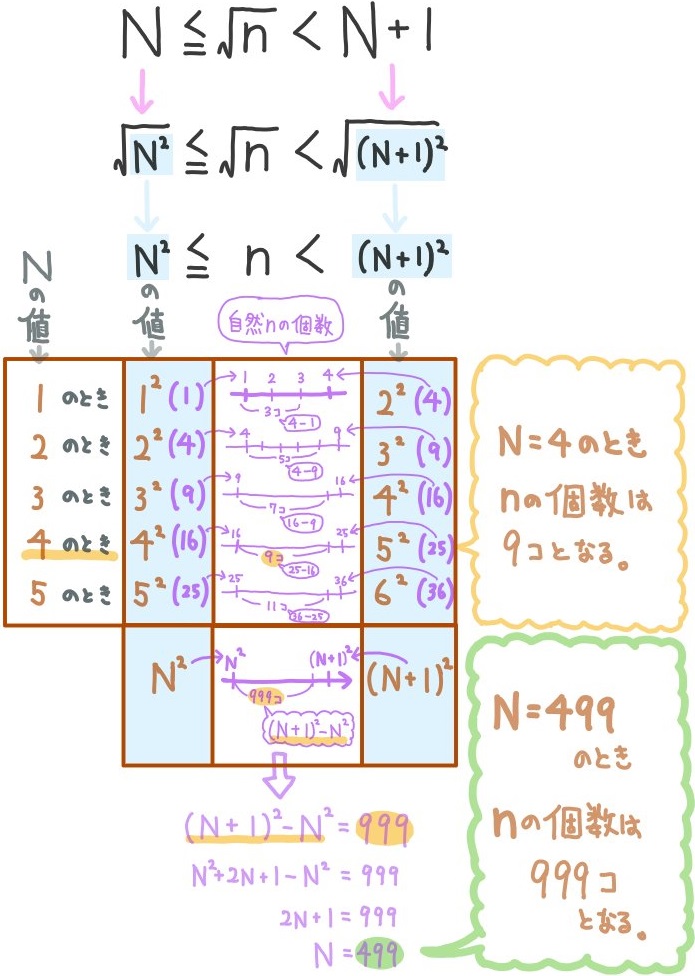
- n、Nを自然数とする。 \(N≦\sqrt{n}<N+1\) を満たすnが9個あるときと999個あるときのNの値をそれぞれ求めよ。
- a、nを自然数とする。 \(n≦\sqrt{a}≦n+3\) を満たすaが70個あるときのn値を求めよ。
- 自然数a、b、cが次の条件を満たすとき、cの値を求めよ。
a×b×c=108
bは \(2\sqrt{10}\) の整数部分
\(\sqrt{17}<a<\sqrt{65}\) - a、b、cは自然数とする。 \(1≦b≦20\) 、 \(\sqrt{ab}=c\sqrt{a}\) が成り立つとき、考えられるcの値をすべて求めよ。
- \(\sqrt{24n}\)は整数とする。 \(\sqrt{24n}<120\)を満たす最大の自然数nを求めよ。

 中学数学の教科書ではあまり登場しない平方根の大小比較の方法です。したがってこのテクニックを知らない場合、難問となります。
中学数学の教科書ではあまり登場しない平方根の大小比較の方法です。したがってこのテクニックを知らない場合、難問となります。nが9個あるときはN=4
nが999個あるときはN=499
 不等号の記号に等号=が含まれている場合といない場合とではその範囲が変わり、したがって、nの個数を求める式も変わります。
不等号の記号に等号=が含まれている場合といない場合とではその範囲が変わり、したがって、nの個数を求める式も変わります。
このような場合、具体的な数値を使って、nの個数を求める式を考えるのがオススメです。(等号があるときとないときで、求め方の式を暗記しても非効率的であまり意味がありません。)


 先程の問題と違うポイントは、平方根の大小関係を表すためのすべての不等号の記号に、等号が含まれているという所です。
先程の問題と違うポイントは、平方根の大小関係を表すためのすべての不等号の記号に、等号が含まれているという所です。
そのため、一番大きな値と一番小さな値の間にある自然数aの個数を求める式が、先程と少し変わっています。
先程の問題では、
大きな値-小さな値=その間の整数の個数
でしたが、この問題では
大きな値-小さな値+1=その間の整数の個数
という式でなければなりません。

たとえば
2≦a≦5
を満たす自然数aの個数は2,3,4,5の4個ですが
単純に
5-2と計算しても3となってしまいます。
なので
5-2+1をすればよいことに気が付けばいい、ということです。

 3つの条件からcを特定していく問題です。一つひとつの条件は基本的な内容ですが、ac=18まで特定できたところで、aの範囲を利用するという所が難しいかもしれません。高校入試問題で出題されうる、平方根の大小関係を利用したやや難問と言えるでしょう。
3つの条件からcを特定していく問題です。一つひとつの条件は基本的な内容ですが、ac=18まで特定できたところで、aの範囲を利用するという所が難しいかもしれません。高校入試問題で出題されうる、平方根の大小関係を利用したやや難問と言えるでしょう。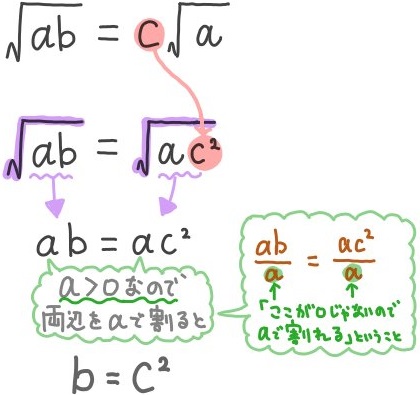








~解き方の流れ~
平方根の大小関係からnの範囲を絞りこみ、\(\sqrt{24n}\)が整数となる条件から、nに含まれる素因数などを絞り込んで検討します。




































