- 小数がある平方根の近似値の問題｜２つの近似値から１つを選ぶパターン
- 平方根の近似値の問題での変形のコツ(←メインの部分)
- 仕上げ用の練習問題
小数がある平方根の近似値の問題｜２つの近似値から１つを選ぶパターン
\(\sqrt{5}=2.236\) 、\(\sqrt{50}=7.071\)として、次の値を求めなさい。
(1) \(\sqrt{500}\)
(2) \(\sqrt{5000}\)
(3) \(\sqrt{50000}\)
(4) \(\sqrt{500000}\)
(5) \(\sqrt{0.5}\)
(6) \(\sqrt{0.05}\)
(7) \(\sqrt{0.005}\)
(8) \(\sqrt{0.0005}\)
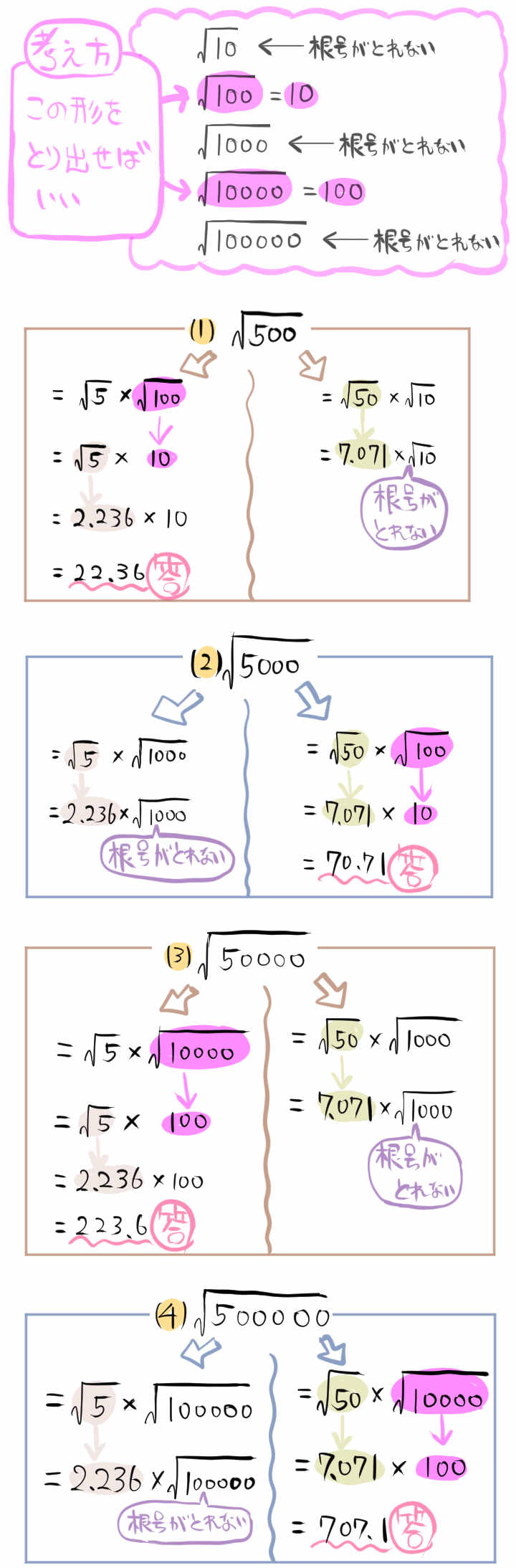
(1)～(4)の解き方の流れ
(1) \(\sqrt{500}\)
(2) \(\sqrt{5000}\)
(3) \(\sqrt{50000}\)
(4) \(\sqrt{500000}\)
\(\sqrt{5}=2.236\)
\(\sqrt{50}=7.071\)
のどちらを使えばいいのか、よくわからなくなる方も多いと思います。
最初の考え方としては、まず式を変形して、 \(\sqrt{100}\) または \(\sqrt{10000}\)のかたちを取り出せないかと考えます。
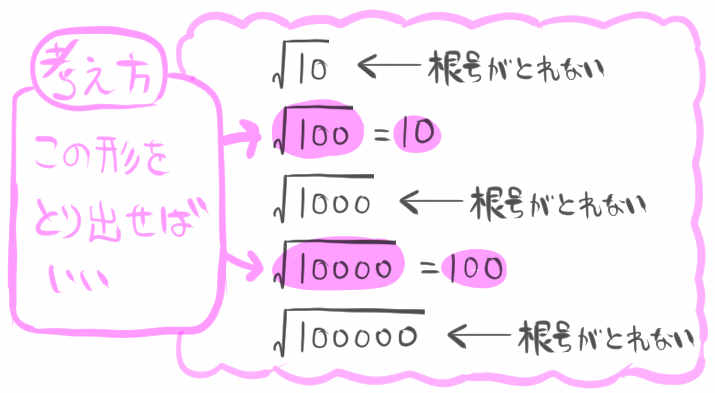
なぜなら \(\sqrt{100}=10\) であるし\(\sqrt{10000}=1000\) となって、平方根がはずれてくれるからです。
逆に、\(\sqrt{1000}\)や\(\sqrt{100000}\)では平方根がはずれてくれないので、この形を取り出してしまうような変形はNGです。
そのようにして考えると、(1)、(2)の問題を２通りに変形できるということがわかります。
そのうち、平方根がはずれる変形の仕方は一方しかないので、そちらの変形が正解ということになります。
(3)、(4)も同じことです。
とりあえず解き方の流れは以上です。
この変形に気が付く方法がありますので、ひき続きご覧ください。
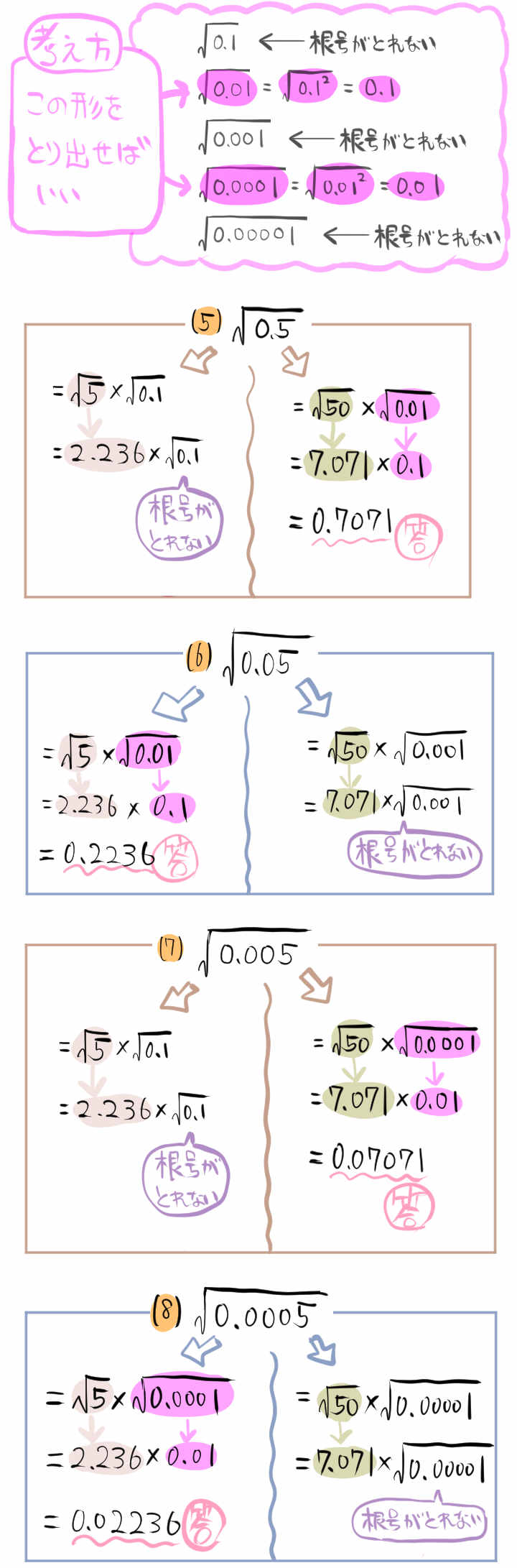
(5)～(8)の解き方の流れ
(5) \(\sqrt{0.5}\)
(6) \(\sqrt{0.05}\)
(7) \(\sqrt{0.005}\)
(8) \(\sqrt{0.0005}\)
こちらも先程と同様、変形によって、次のかたちを取り出せないかと考えます。
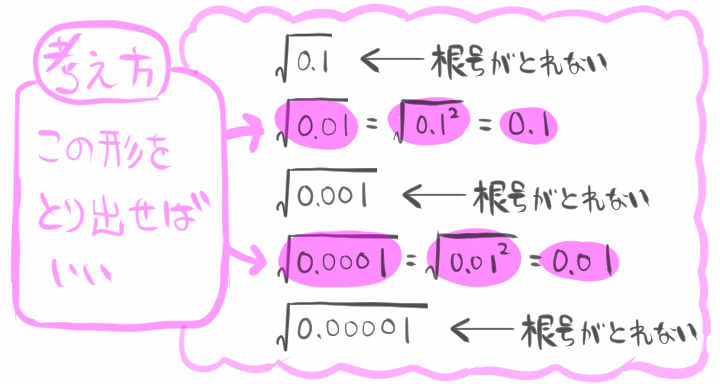
０の数がややこしい場合は『０の数が２個や４個のように偶数個あったら、平方根がはずれる』と覚えておいてもいいでしょう。
\(\sqrt{0.01}\)は０の数が２個あり、\(\sqrt{0.0001}\) は０の数が４個あるので平方根がはずれる、という具合です。
小数のかたちの問題でも、(1)(2)のように２通りの変形ができます。
一方では平方根がはずれて、一方でははずれないということになります。
(5)(6)は\(\sqrt{0.01}\)の形を取り出して平方根をはずす問題でした。
つづいて(7)(8)は\(\sqrt{0.0001}\)の形を取り出して平方根をはずします。
ただ、そもそもこの変形ができないし、わからないという場合もあると思います。
なので、次は『変形のコツ』について解説します。
平方根の近似値の問題での変形のコツ
ざっと問題と解き方の流れの意味が理解できたところで、ここから本題に入ります。
『変形のコツ』です。
この問題で説明します。
(1) \(\sqrt{150}\)
(2) \(\sqrt{1500}\)
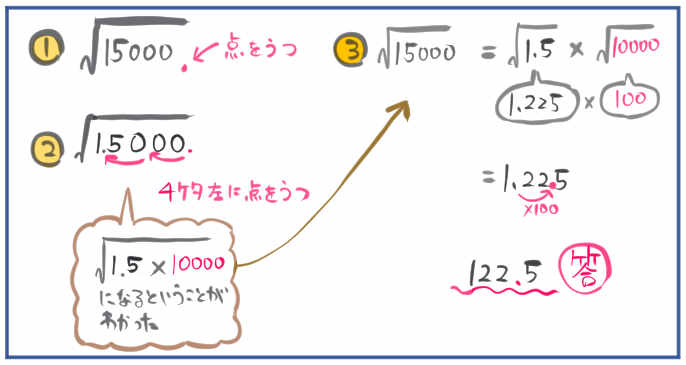
(3) \(\sqrt{15000}\)
(4) \(\sqrt{0.015}\)
(5) \(\sqrt{0.0015}\)
先程までに説明していた方法で解くとこうなります。
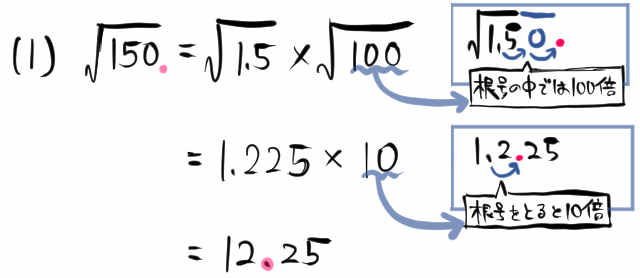
このなかの『根号のなかでは100倍』のところを見てください。
\(\sqrt{1.5}\) を \(\sqrt{100}\) 倍する計算は、根号のなかだけを見ると
\(1.5\times 100\) というように100倍の計算になっています。
\(\sqrt{100}\) 倍は、根号をとると10倍のことです。
『根号をとると10倍』のところを見ると、 \(\sqrt{1.5}\) の近似値である1.225を10倍しています。
ルートのなかでは100倍の計算
なのが
ルートなしの形だと10倍の計算
まず、このことを納得しておいてください。
これを見てください。
よく、教科書やワークなどの説明のところに、こんなものがあったりします。
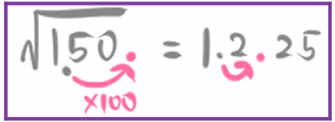
これってわかりにくいですよね。（わかるようなわからないような。）
過程の説明が抜けているんですね。
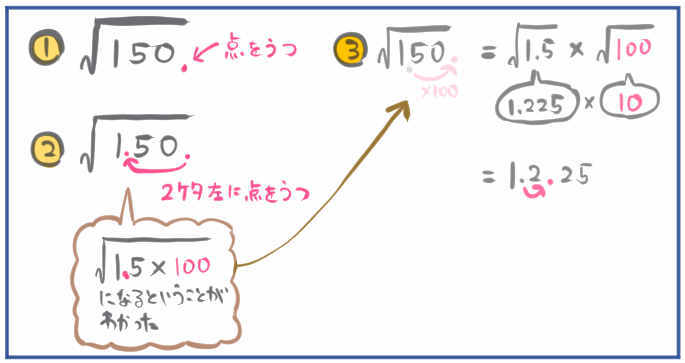
過程まで説明するとこうなります。
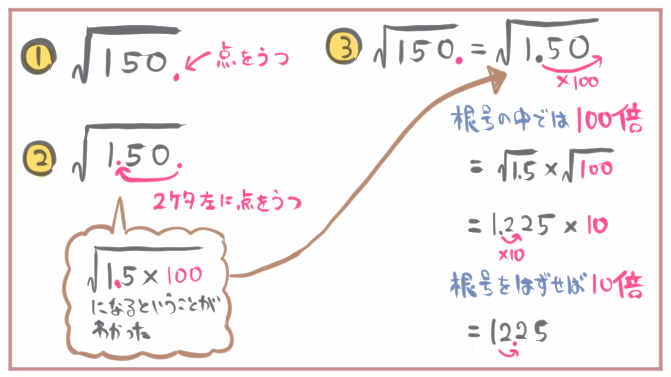
- 小数点を打ちます。
150は整数だったので小数点を書いておく必要はありませんでしたが、本来小数点があるはずの位置である１の位の右下に小数点を打ちます。 - ２桁左に点を小数点を打ちます。
先程打った小数点よりも２桁左に小数点を移動させます。すると、１と５の間に点が移動して1.5という形が表れました。
『左へ2桁点を移動させる操作』は『100分の1にする操作』と同じことです。
『100分の1にする操作』をして1.5という形が表れたということは、逆に言えば1.5を100倍すると、もとの小数点の位置にもどって150にもどるということです。
つまり150は1.5×100に変形できるということがわかったということです。
さらにこれは、根号のなかの話なので、正確には\(\sqrt{150}\) は \(\sqrt{1.5\times 100}\) に変形できるということがわかったということです。
- \(\sqrt{150}\) ＝ \(\sqrt{1.5}\times \sqrt{100}\) に変形する。
\(\sqrt{150}\)のところに書き込んである黒や赤の小数点は、根号の中の1.5を100倍すると150になるという説明のためのものです。
\(\sqrt{150}\) ＝ \(\sqrt{1.5}\times \sqrt{100}\)に変形できたら、あとは、\(\sqrt{1.5}=1.225\)、\(\sqrt{100}=10\)なので計算して完了です。
と、ここまでの説明が理解できたところでこちらをもう一度見てください。
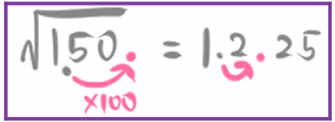
③のところの『最初と最後の部分』を取り出してつなげた式になっています。
この短い説明が言いたかったことはこうです。
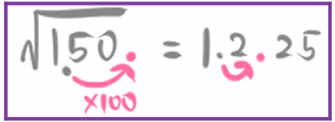\(\sqrt{150}\) は \(\sqrt{1.5}\times \sqrt{100}\)ですよ。
\(\sqrt{1.5}\)を\(\sqrt{100}\)倍すると\(\sqrt{150}\) になりますよ。
\(\sqrt{100}\)倍するということは、根号のなかの計算では100倍するということですよ。つまり２桁分の点の移動をするということですよ。
\(\sqrt{100}\)は10なので、\(\sqrt{100}\)倍は（その根号をはずして計算するなら）10倍するということですよ。
\(\sqrt{150}\) は \(\sqrt{1.5}\)の\(\sqrt{100}\)倍でしたよね。
\(\sqrt{1.5}\)は1.225
\(\sqrt{100}\)は10
なので、
\(\sqrt{150}\) は1.225×10ですよね。
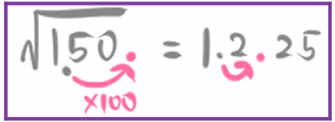つまり
平方根のなかをみると1.5を100倍すれば150になるので
根号をとった状態では1.225(\(\sqrt{1.5}\))を10倍(\(\sqrt{100}\)倍)すればいいのですよ。
(1) \(\sqrt{150}\)
(2) \(\sqrt{1500}\)
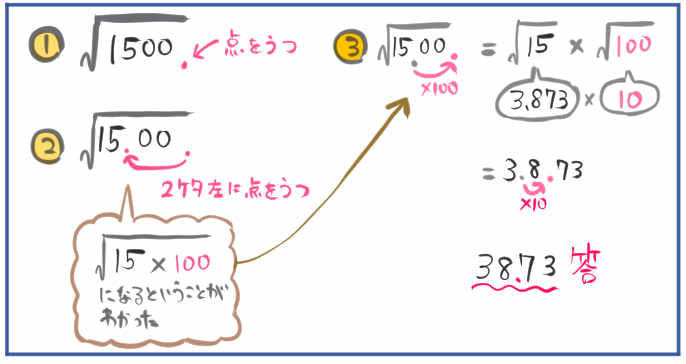
(3) \(\sqrt{15000}\)
(5) \(\sqrt{0.0015}\)
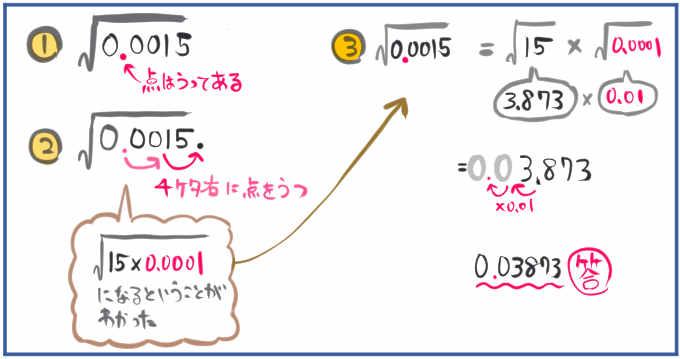
変形のコツ｜小数が登場する場合
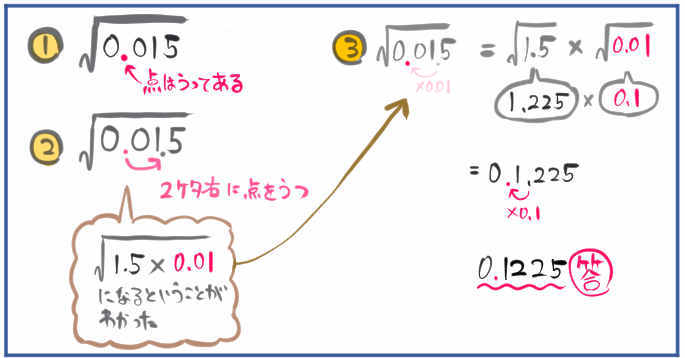
(4) \(\sqrt{0.015}\)
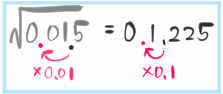
さきほどと同じ手順を踏んでゆくので、イメージもしやすいかと思います。
これは、\(\sqrt{0.015}\)の根号のなかの計算だけで見れば0.015は1.5×0.01ということがわかります。
つまり、\(\sqrt{0.015}\)は\(\sqrt{1.5}\)×\(\sqrt{0.01}\)ということなので
\(\sqrt{1.5}\)=1.225
\(\sqrt{0.01}\)=0.1
というように根号をとった計算になおすと
\(\sqrt{0.015}\)=1.225×0.1となり
0.1225となります。
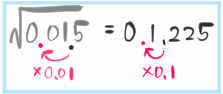根号の中の計算では0.01倍だったのが、平方根なしの計算で見たときに0.1倍の計算だよね。
さっきの解説を見てみましょう。
②のところで、２桁小数点を右に動かして、何と何の掛け算に分解できるか見つけています。
(4) \(\sqrt{0.015}\)
この問題では、２桁小数点を右に動かすだけでは、\(\sqrt{1.5}\)や\(\sqrt{15}\)の掛け算のかたちに分解できなかったので、さらに２桁右に動かしています。
(5) \(\sqrt{0.0015}\)
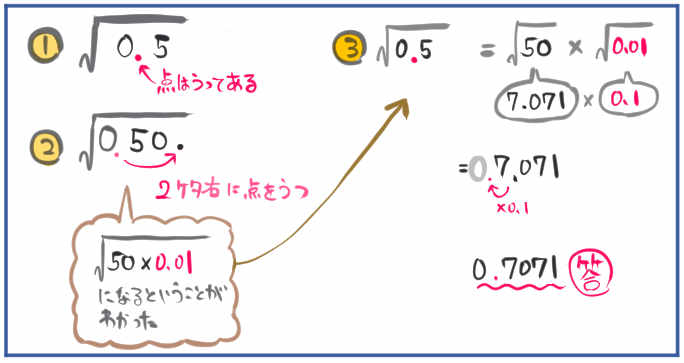
(5) \(\sqrt{0.5}\)
仕上げ用の練習問題
さいごに練習問題です。
解き方は、これまで説明した通りです。
\(\sqrt{11}=3.317\) 、\(\sqrt{110}=10.448\) として、次の値を求めなさい。
(1)\(\sqrt{11000}\)
(2)\(\sqrt{0.11}\)
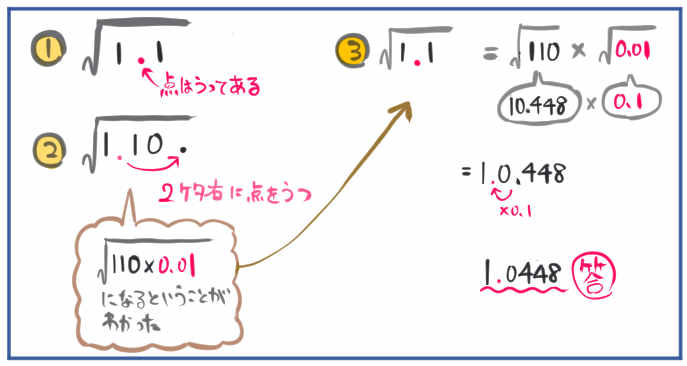
(3)\(\sqrt{1.1}\)
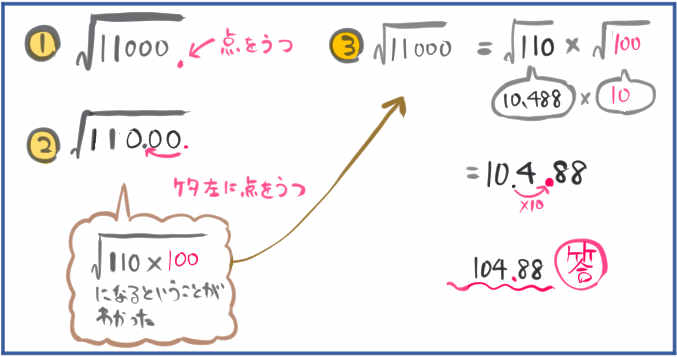
(2)の解説
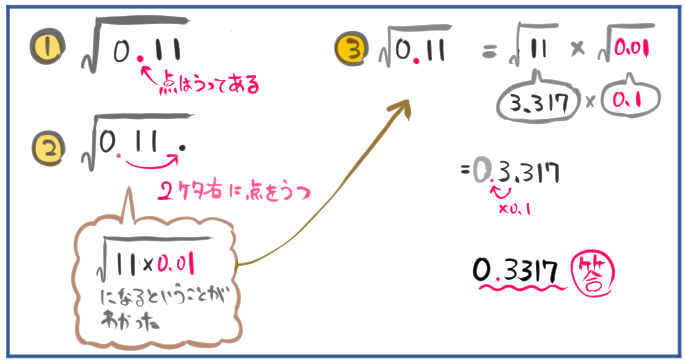
(3)の解説
(1) \(\sqrt{150}\)
(2) \(\sqrt{1500}\)
(3) \(\sqrt{15000}\)
(4) \(\sqrt{0.015}\)
(5) \(\sqrt{0.0015}\)