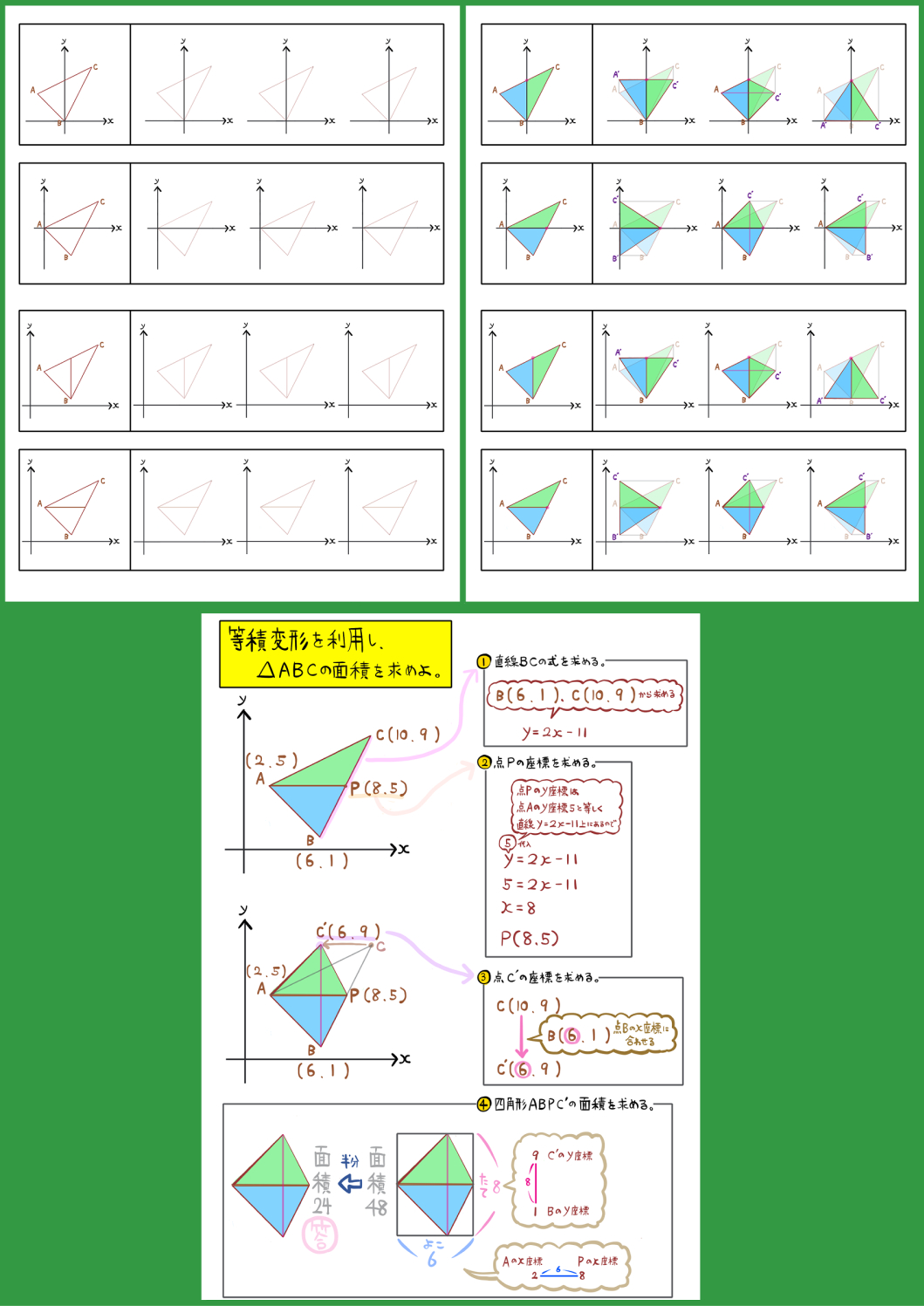
ｙがｘの２乗に比例する関数のグラフ｜標準～難問
図のように、ｙがｘの２乗に比例する関数のグラフ \(y=x^{2}\)と直線ℓは２点Ａ、Ｂで交わっている。
２点A、BのX座標はそれぞれ－１、３である。
△ＡＢＣの面積が△ＯＡＢの面積の２倍となるとき、点Ｃのｘ座標を求めよ。
ただし、点Cはｘ軸上の点とし、点ＣのX座標は正とする。
（明訓高校の高校入試の過去問：改）
△ＡＢＣの面積が△ＯＡＢの面積の２倍となるとき、点Ｃのｘ座標を求めよ。
ただし、点Cはｘ軸上の点とし、点ＣのX座標は正とする。
まずは直線ABの方程式を求めます。
次に直線ABに対して平行で、なおかつ点ｃを通る補助線を書き加えます。
その補助線とｙ軸との交点を点Eとします。
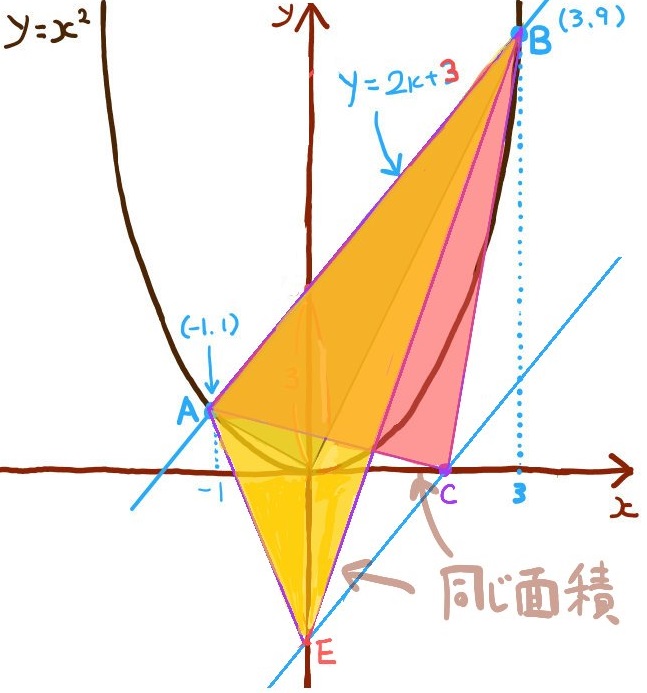
すると、△ABCと△ABEの面積が同じになります。
なので、まずは△ABEの面積が△OABの面積の２倍になるような点Eを求めます。
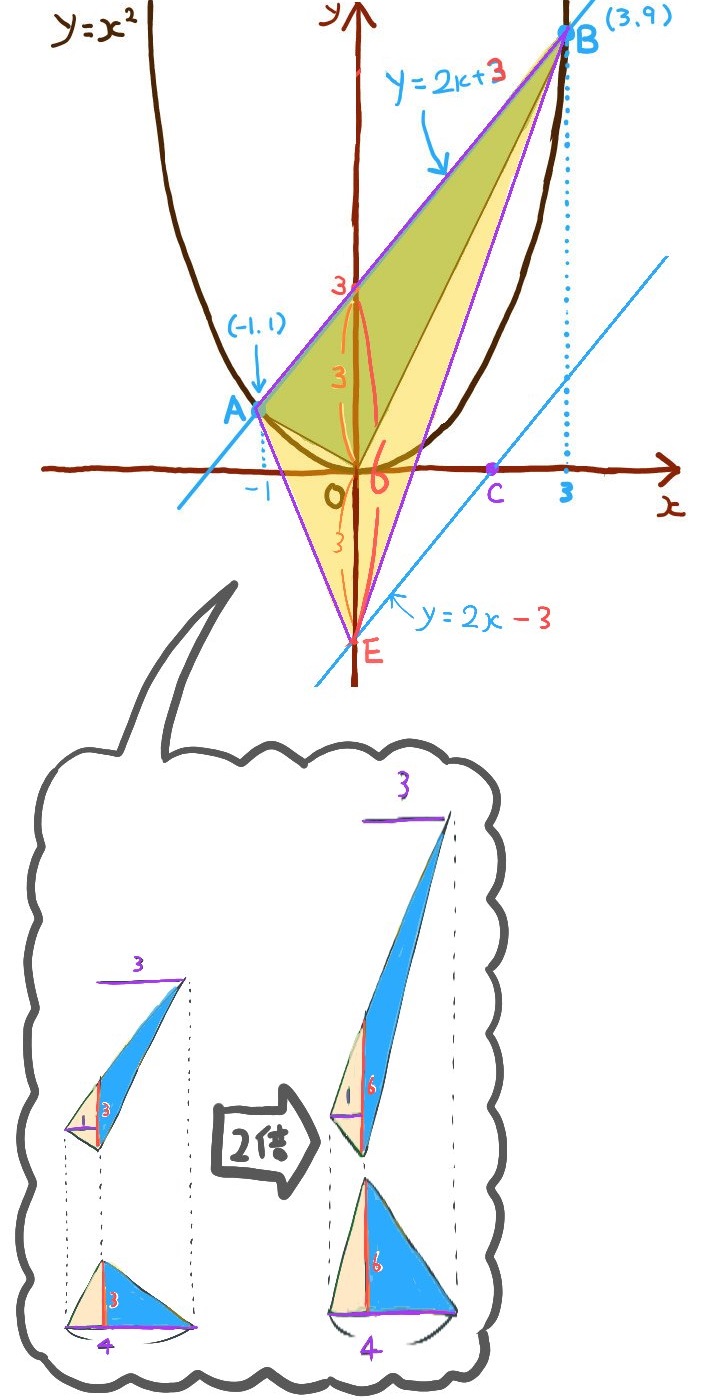
点Eを求めることで、書き加えた補助線の方程式がわかります。
※傾きは直線ABと同じで、ｙ切片は点Eのｙ座標です。
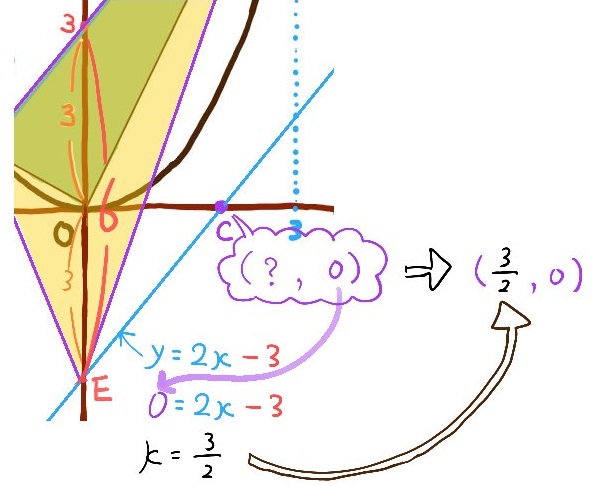
その補助線の方程式とｘ軸とが交わる交点のｘ座標を求めます。（直線の方程式にy=0を代入します。）
これが求める点Ｃのｘ座標になります。
直線の方程式と、放物線の方程式の交点を求める場合、それら二つの式を連立方程式で解きましょう。それによって得られたｘの値とｙの値が交点の座標になります。交点が二か所ある場合は、ｘの値もｙの値も２つずつ得られることになります。その２か所の座標のうち、問題の条件に適したものを選びます。
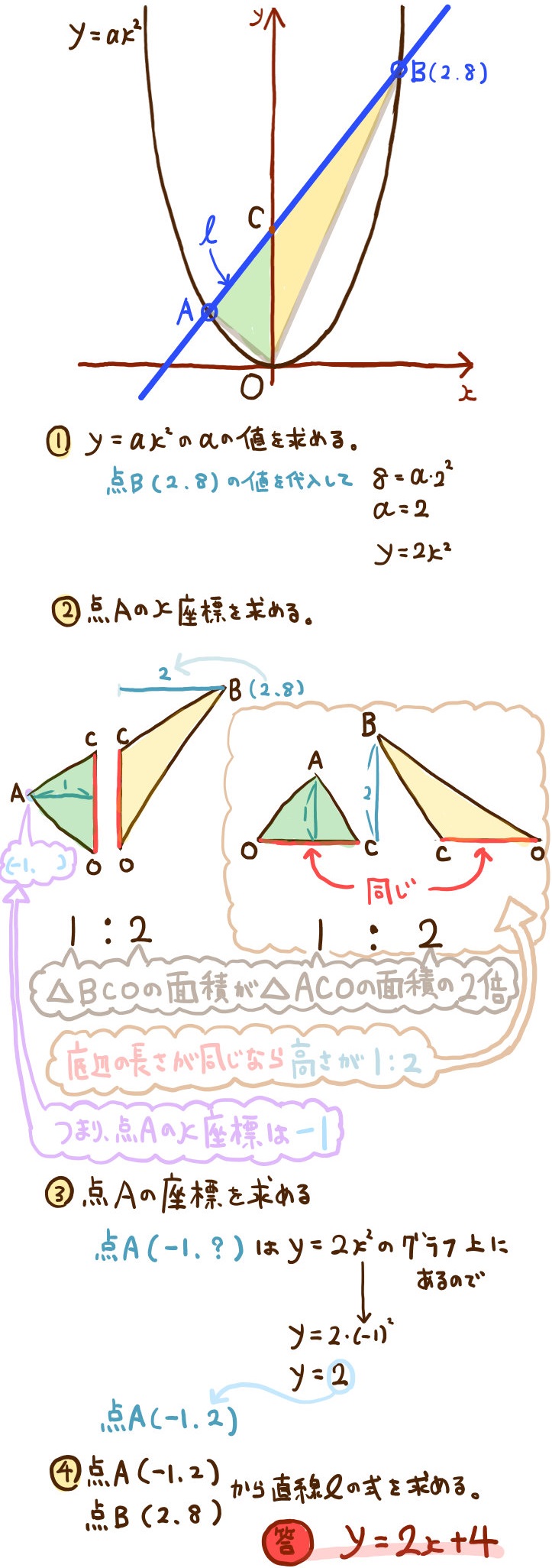
図のような放物線 \(y=ax^{2}\) のグラフと、直線ℓの交点をA、Bとする。
直線ℓとｙ軸とは点Ｃで交わっている。
点Ｂの座標は（２，８）である。
△ＢＣＯの面積は△ＡＣＯの面積の２倍である。
（１）直線ℓの方程式を求めよ。
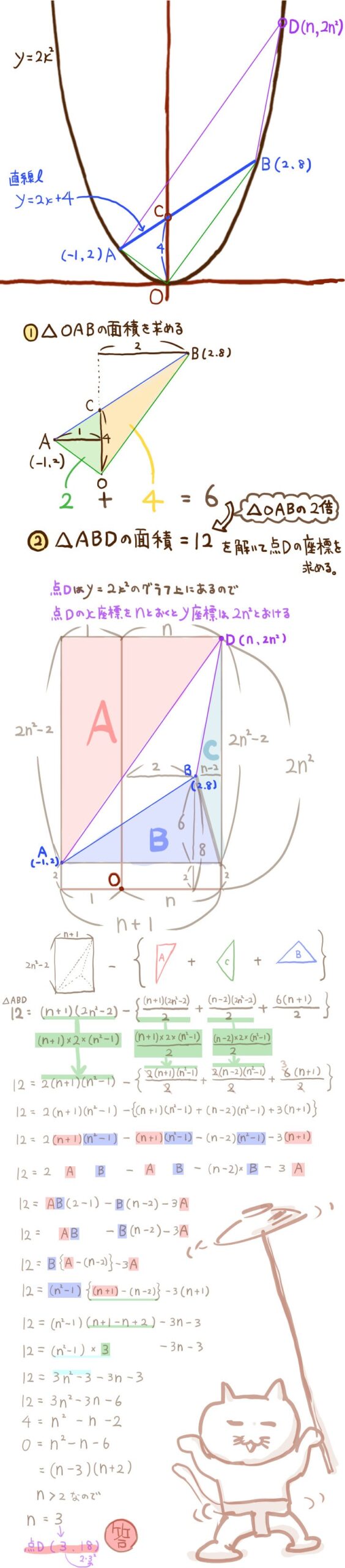
（２）放物線 \(y=ax^{2}\) のグラフ上にある点Dが、ｘ座標が２より大きく、なおかつ、△ＡＢＤの面積が△ＯＡＢの面積の２倍であるという条件を満たす。このとき、点Ｄの座標を求めよ。
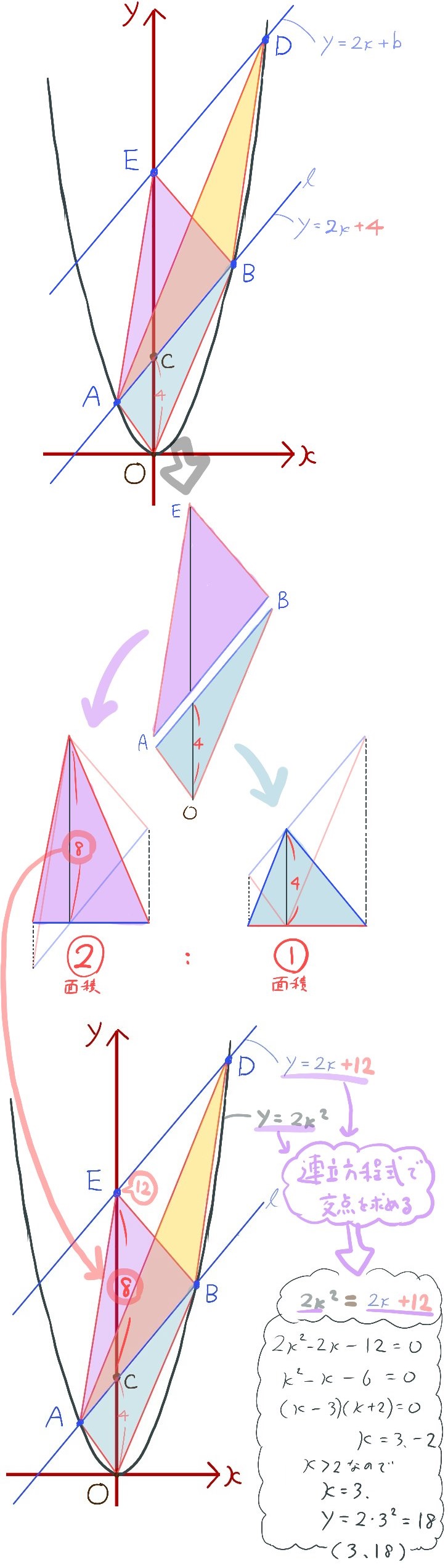
平行線を補助線に引き、まずはその補助線の方程式を求めます。その後、その補助線と放物線の交点の座標を求めることで解答へと至るパターンです。なぜ、補助線が有効かというと、後半でご紹介する別解を参考にしてください。普通に解いたら手間がかかってしまうということがわかるでしょう。次の問題もそのようなコンセプトです。
図のように、ｙがｘの２乗に比例する関数 \(y=ax^{2}\) のグラフと直線ℓの交点をA、Bとする。
直線ℓとｙ軸との交点をＣとする。
点Ａの座標は（－８，－１６）である。
点Ｂのｘ座標は正で、ｙ座標は－１である。
（１）直線ℓの方程式を求めよ。
（２）△BOCと△AOCの面積比を最も簡単な整数の比で表せ。
（３）放物線上の点Oから点Aまでの部分に、点Pを△APCの面積が△AOBの面積の\(\dfrac{4}{5}\)倍になるようにとる。このときの点Pの座標を求めよ。ただし点Pは点O、点Ａのどちらとも異なるものとする。
解法パターン１：二つの三角形の面積を求めて比を求める方法
解法パターン２：二つの三角形の高さの比を利用する方法
まず、△AOBの面積を確認しておきます。
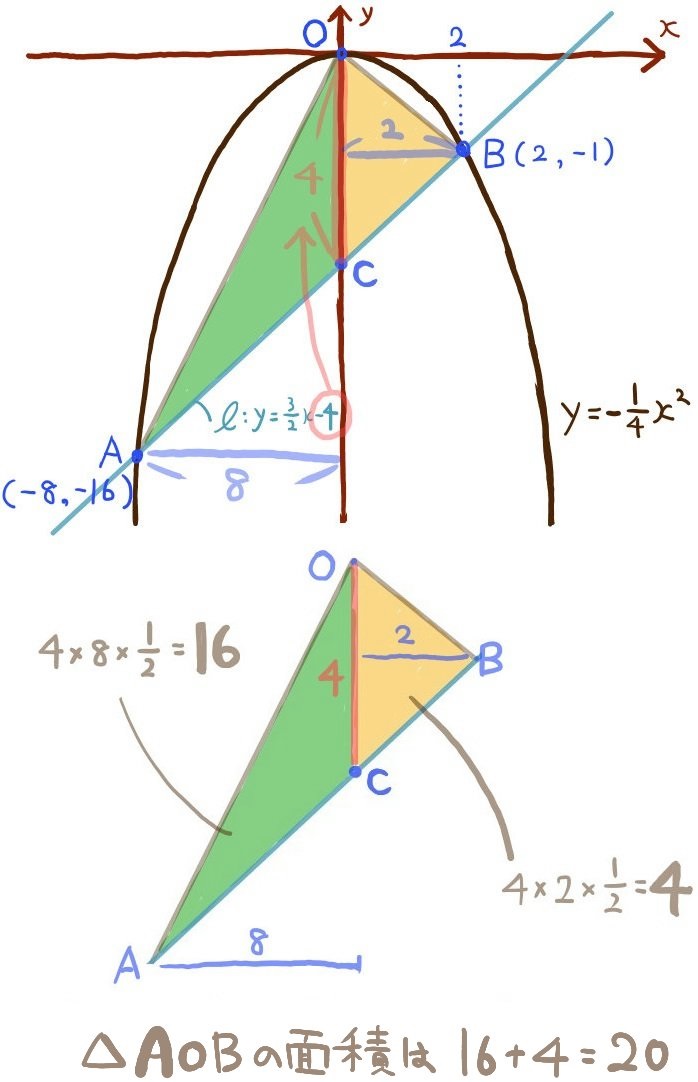
以上により、△AOBの面積は20となります。
直線ℓに平行で、点Pを通る補助線を以下のように書き込み、補助線とｙ軸との交点をEとします。
△APCの面積と△AECの面積が等しいので、△AECの面積が△AOBの面積20の５分の４倍になる点Eを求めます。
書き込んだ補助線の方程式のy切片を−nとすると、線分ECは4-nと表現できます。
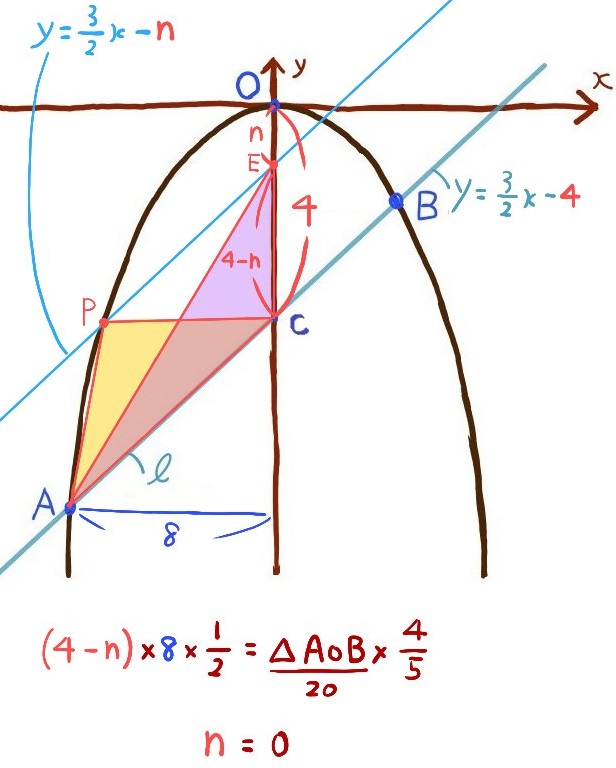
方程式を解いた結果、nの値が0ということは『補助線のy切片が0』だということ、つまり、補助線は原点oを通るということです。
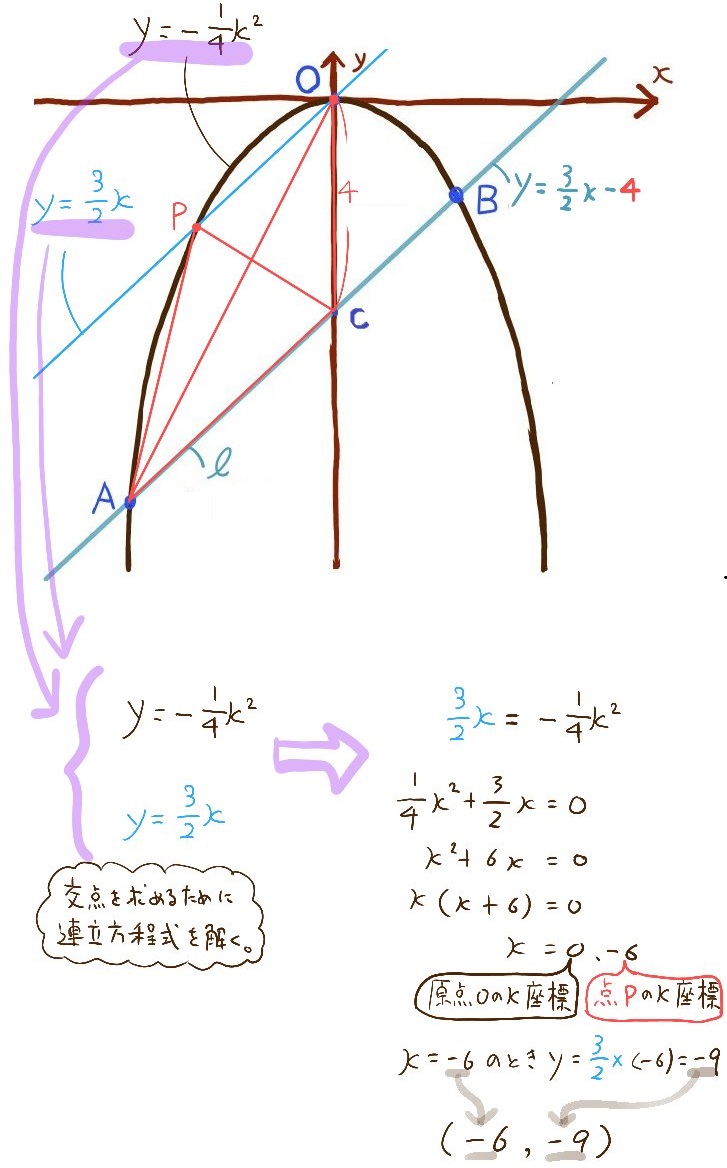
補助線と放物線の交点が求める点Pの座標なので、連立方程式で解き、完了です。
放物線のグラフの応用問題の解き方｜別解編
答：（３，１８）
解説：３点から三角形の面積を求める公式｜必須テクニックも紹介
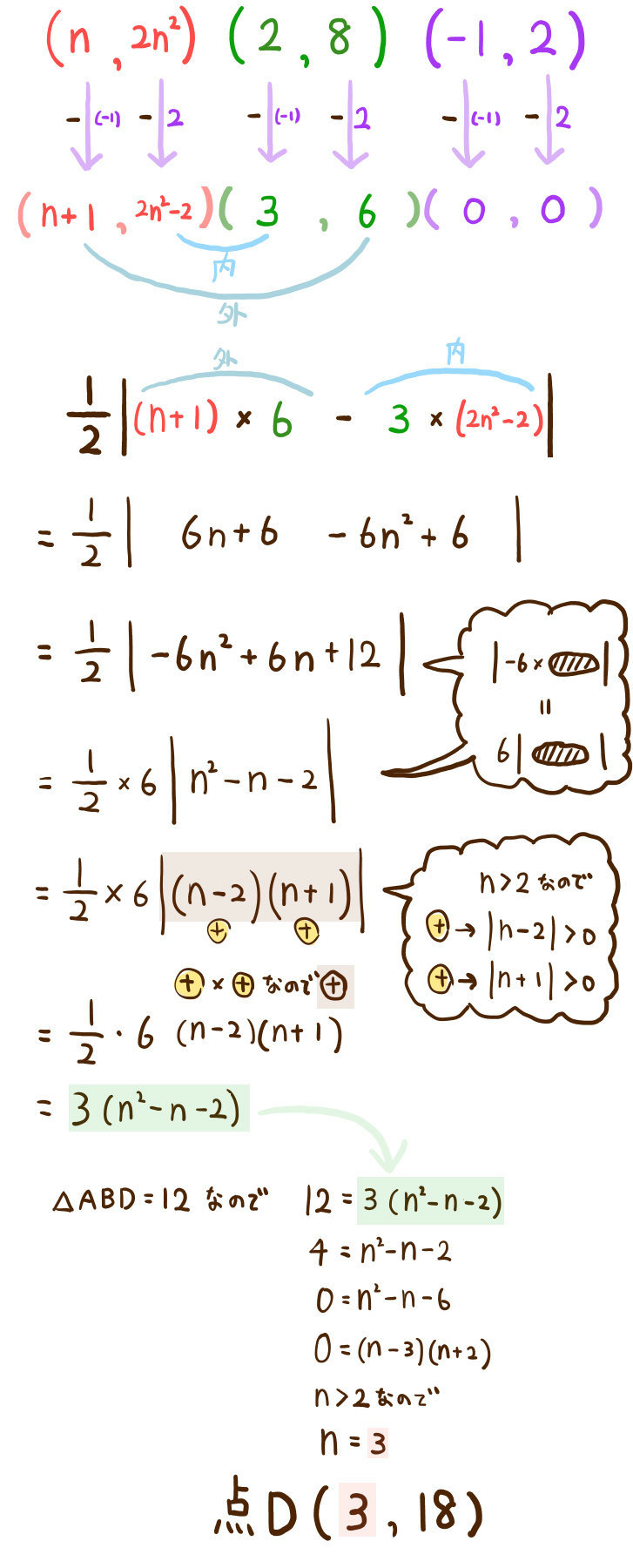
この解法の利点について
答：（－６，－９）
答：（－６，－９）
解説：３点から三角形の面積を求める公式｜必須テクニックも紹介
絶対値の記号を外す練習問題と解説
