


- 平方根の整数部分と小数部分の解き方のコツ|わかりやすい解説
- 平方根の小数部分|ルートの練習問題~難問
- 平方根の整数部分|ルートの練習問題~難問
平方根の整数部分と小数部分の解き方のコツ|わかりやすい解説

\(\sqrt{5}\) の整数部分と小数部分を求めよ。
ルート5=2.236‥
なので、整数部分は2です。



\(\sqrt{5}\) は\(\sqrt{4}\) (つまり2)と\(\sqrt{9}\) (つまり3)の間にある値だということがわかります。
2と3にある値の整数部分は2なので、\(\sqrt{5}\) の整数部分は2ということです。
このことから次のような関係がわかります。

このように、当たり前の話ですが
\(\sqrt{5}\)は\(\sqrt{5}\)の整数部分と\(\sqrt{5}\)の小数部分の和でできています。
この方程式を変形してみます。

このように
\(\sqrt{5}\)の小数部分=\(\sqrt{5}\)-\(\sqrt{5}\)の整数部分
という方程式になり、ルート5の小数部分の値を表現することができます。
このように
\(\sqrt{a}\)の小数部分=\(\sqrt{a}\)-\(\sqrt{a}\)の整数部分
という考え方は、ルートの記号がついた値の小数部分を求める際によく使うので、覚えておいてください。

平方根の小数部分|ルートの練習問題~難問
平方根の整数部分|ルートの練習問題~難問
\(\sqrt{n}\)の整数部分が2になるとき、自然数nの値をすべて求めよ。ただし、nは4より大きい値とする。
 平方根の整数部分が2であるということは、それがちょうど2であっても整数部分は2ということになります。しかし、その場合のnは4であるので除外します。よって、自然数nの値は、2から3の間について調べればいい、ということになります。
平方根の整数部分が2であるということは、それがちょうど2であっても整数部分は2ということになります。しかし、その場合のnは4であるので除外します。よって、自然数nの値は、2から3の間について調べればいい、ということになります。\(\sqrt{2x+1}\) の整数部分が5になるような整数\(x\)の値をすべて求めよ。
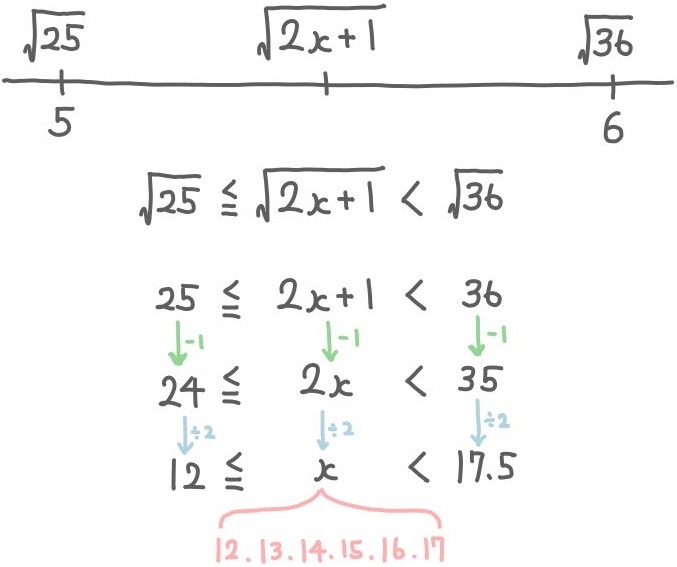
\(\sqrt{n}\)の整数部分を\(p\left( n\right) \)とするとき、\(p\left( n\right) +p\left( n+1\right) =5\) を満たす自然数nを求めよ。
このように、表を作って検討するとnを発見しやすいです。
 ルート8の整数部分は2であり、ルート9の整数部分は3となり、n=8のとき、\(p\left( 8\right) +p\left( 8+1\right) =5\) が成立します。
ルート8の整数部分は2であり、ルート9の整数部分は3となり、n=8のとき、\(p\left( 8\right) +p\left( 8+1\right) =5\) が成立します。
よって、答えはn=8となります。
\(\sqrt{n}\)の整数部分を\(p\left( n\right) \)とするとき、\(p\left( n\right) +p\left( n+1\right) =4\) を満たす自然数nをすべて求めよ。
 先程の問題は\(p\left( n\right) +p\left( n+1\right) \)が奇数5になる問題でした。この問題は\(p\left( n\right) +p\left( n+1\right) \)が偶数4になる問題です。
先程の問題は\(p\left( n\right) +p\left( n+1\right) \)が奇数5になる問題でした。この問題は\(p\left( n\right) +p\left( n+1\right) \)が偶数4になる問題です。
このように、奇数である場合は、平方根の整数部分が変わるところに求めるnがあり、偶数である場合は求めるnは複数存在することになります。
\(\sqrt{n}\)の整数部分を\(p\left( n\right) \)とする。
数列\(p\left( 1\right) \) , \(p\left( 2\right) \) , \(p\left( 3\right) \) , ‥ , \(p\left( 50\right) \)の和を求めよ。

平方根の整数部分をすべて書き出していてはきりがないので、解説のように表にして考えると計算しやすくなります。





































\(\sqrt{20}\) の小数部分を \(x\) とするとき、\(\left( x+1\right) \left( x+7\right)\)の値を求めよ。
そのあと、求める値を計算します。
\(\sqrt{10}\) の小数部分を \(x\) とするとき、\(x\left( x+6\right) \) の値を求めよ。
ルート10の整数部分を求めてから、小数部分を求めます。
そのあと、求める値を計算します。
\(\sqrt{2}\) の小数部分を \(a\) とし、\(\sqrt{8}\) の小数部分を \(b\) とする。このとき\(\dfrac{b}{a}\) の値を求めよ。
bは2aということがわかりましたので、そのまま代入して、答えは2となります。
\(\sqrt{3}+2\) の整数部分をa、小数部分をbとするとき、 \(b^{2}+\dfrac{2}{3}ab\) の値を求めよ。
まずは \(\sqrt{3}\) の整数部分が1であることを調べ、そこから\(\sqrt{3}+2\) の整数部分aが3であることを求めます。
(法政大学高校)
\(4-\sqrt{7}\) の小数部分を\(x\) とするとき、\(x\left( x-6\right) \) の値を求めよ。
\(\sqrt{2016}\) の整数部分を求めよ。また、\(\sqrt{2016}\)の小数部分を \(x\) とするとき、\(x^{3}+89x^{2}+8x\)の値を求めよ。
これで整数部分が平方根の記号が付いた値の整数部分が求まりました。
つまり、小数部分は \(\sqrt{2016}-44\) ということになります。
ここからは、この平方根の小数部分についての計算式を、工夫して解く方法をご紹介します。
このように、3乗の式があるような複雑な問題の場合は、値を代入していって、徐々に係数を下げていく方法が有効な場合があります。
(星光学院高校)
\(a\) は2桁の素数とし、\(\sqrt{a}\) の整数部分をnとする。\(\dfrac{1}{\sqrt{a}-n}=\sqrt{a}+n\) が成り立つとき、aの値を求めよ。
(西大和学園高校)
\(\left( \sqrt{3}+\sqrt{5}\right) ^{2}\) の小数部分をxとするとき、\(x^{2}+14x\)の値を求めよ。
(慶應義塾志木高校)
既約分数 \(\dfrac{b}{a}\) がある。 \(a+b=1234\) であり、この分数の平方根の小数部分を切り捨てると10になる。この分数を求めよ。
既約分数 \(\dfrac{b}{a}\)の平方根 \(\sqrt{\dfrac{b}{a}}\) の小数部分を切り捨てた値、すなはち整数部分が10になるということなので
\(10\leqq \sqrt{\dfrac{b}{a}} <11\)
(慶應義塾志木高校)