にゃんこ
ここでは正六角形の内角の和の求め方と、一つの内角や一つの外角の求め方について解説します。
このページの内容
- 正六角形の内角の和の求め方３パターン
- 正六角形の一つの内角の求め方２パターン
- 正六角形の一つの外角の求め方
- 正六角形の一つの外角と一つの内角の和は180°
にゃんこ
中学数学のまとめプリント(無料)はこちら。
正六角形の内角の和の求め方３パターン
坂田先生
内角の和というのは、その図形の内側にある角度の合計のことを指します。（この後に登場する図を見るとわかりやすいです）
にゃんこ
正六角形の内角の和について、２通りの求め方を解説します。
正六角形の内角の和の求め方１｜正三角形で考える場合
にゃんこ
正六角形は、次のように正三角形が６つ詰まった図形と見ることができます。
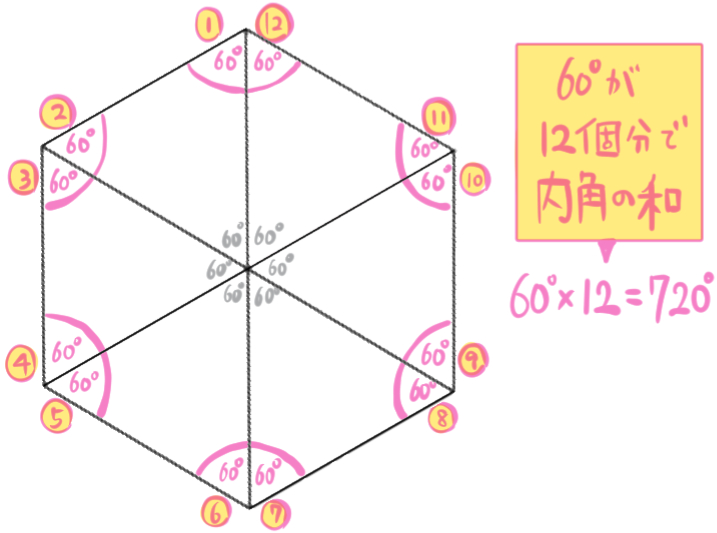
にゃんこ
正三角形はどの角の大きさも60°です。
坂田先生
なので、正六角形の内角をすべて集めた合計は、上の図のように60°の12個分だと考えることができます。
にゃんこ
60°が12個分で合計720°ですね。
正六角形の内角の和の求め方２｜三角形の数で計算する場合
坂田先生
次は、三角形の内角の和４つ分だと見て求める方法です。
にゃんこ
このように、正六角形（または六角形）は三角形３つが集まった図形と見ることができます。
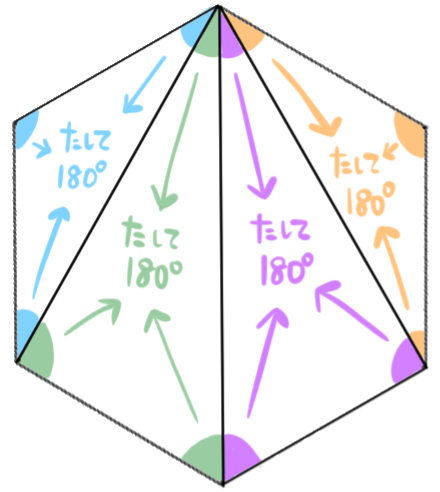
坂田先生
１つの三角形の内角は全部で180°になります。
にゃんこ
その三角形４つ分の内角の合計が、正六角形の内角の和と等しくなっていますね。
坂田先生
よってこのように、180×4=720という計算で求めることができます。
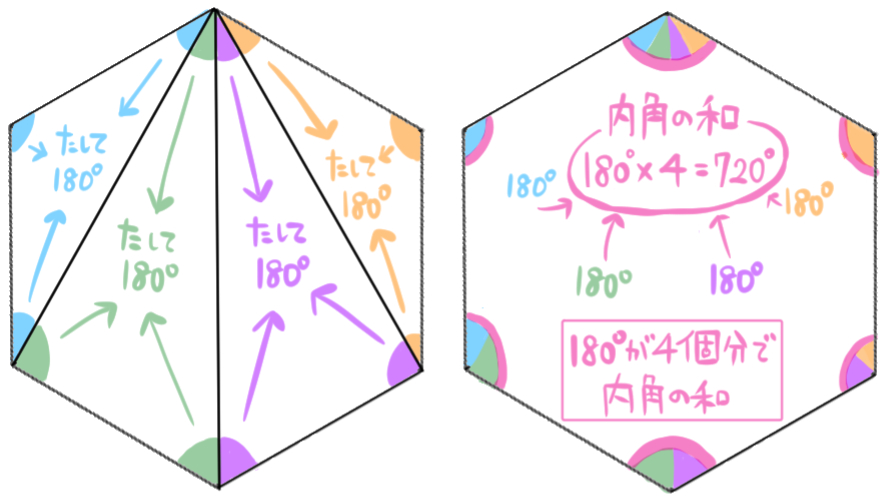
このように、正六角形（または六角形）は、三角形４個からできる図形と見ることができます。
では、他の多角形では、三角形何個でできているか？についてまとめてみると、こうなります。
多角形がそれぞれ三角形何個分であるかという数と、それをもとに内角の和を求める式もまとめてあります。
坂田先生
では、上の表をもとに、七角形や、十二角形、ｎ角形では内角の和は、どうなるのでしょうか。
にゃんこ
答えはこうです。
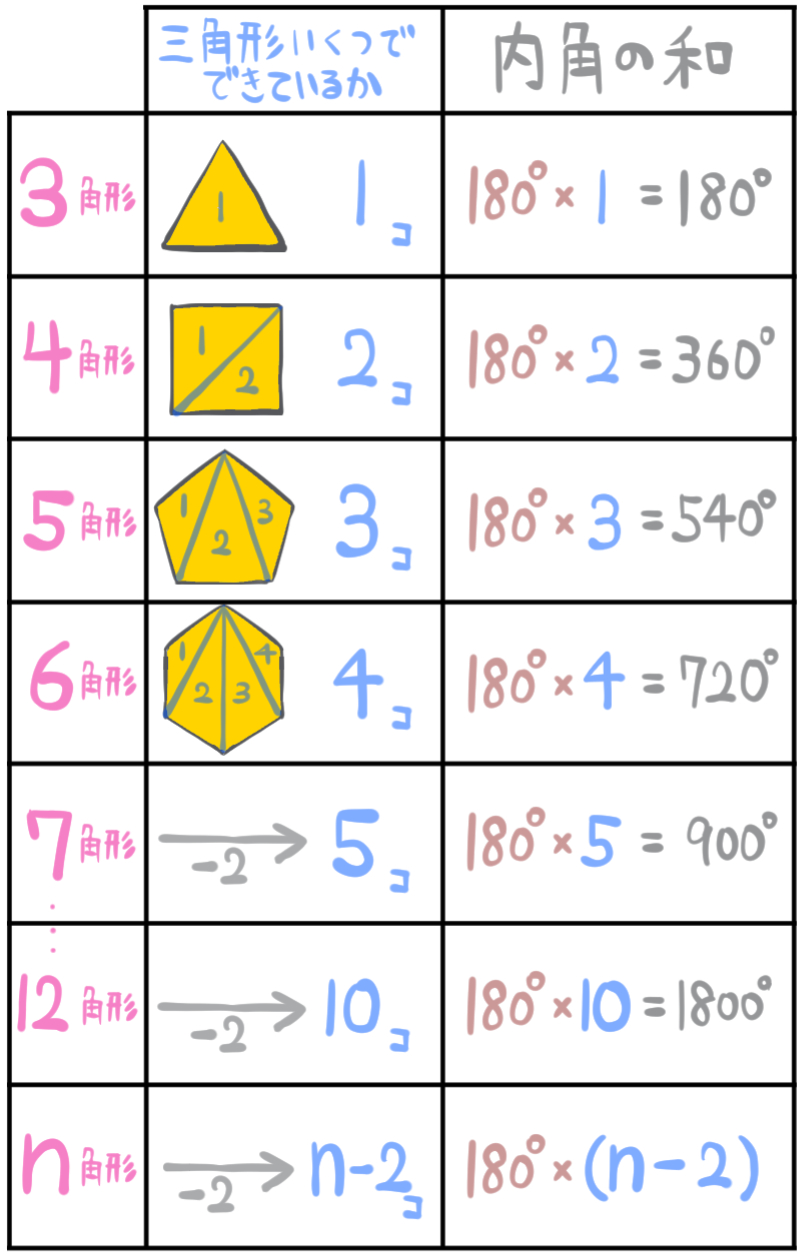
例えば七角形の場合、７から２を引いた結果である５個の三角形でできています。
十二角形の場合は、１２から２を引いた結果である１０個の三角形でできています。
このように？角形の場合、この？から２を引いた数の三角形からできているということです。
そう考えるとｎ角形の場合は、ｎから２を引いた数であるn-2(個)の三角形からできています。
にゃんこ
なので、ｎ角形の内角の和は180にn-2をかけた式になっているのです。
ｎ角形の内角の和
\(180\left( n-2\right) \)
または、その式を展開した
\(180n-360\)
坂田先生
この公式を覚えておいて、ｎの部分に６を代入するという方法でも、正六角形(または六角形)の内角の和を求めることができます。
正六角形の内角の和の求め方３｜公式に代入する場合
ｎ角形(または正ｎ角形)の内角の和の公式
\(180\left( n-2\right) \)
または
\(180n-360\) ←かっこをはずした式
坂田先生
この公式を利用して、正六角形または六角形の内角の和を求めようとする場合、このように計算します。
にゃんこ
このどちらの式に代入してもいいです。
正六角形の一つの内角の求め方２パターン
坂田先生
ここからは、正六角形の一つの内角の大きさを求める方法について解説します。
にゃんこ
さっき解説した『内角の和』というのは、内側にある角度の合計でした。
坂田先生
次はそうではなく、内角一つ分の大きさを求めるということです。
正三角形６つでできた正六角形と見る方法
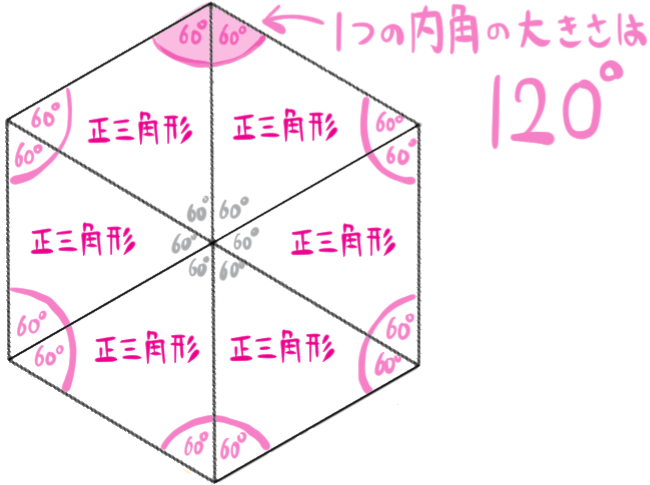この図のように考えると、正六角形の内角一つ分の大きさは60°の２個分なので120°となります。
内角の和を均等に６等分する方法
こちらは、先に正六角形の内角の和720°を求めてから、それを６で割るという方法です。
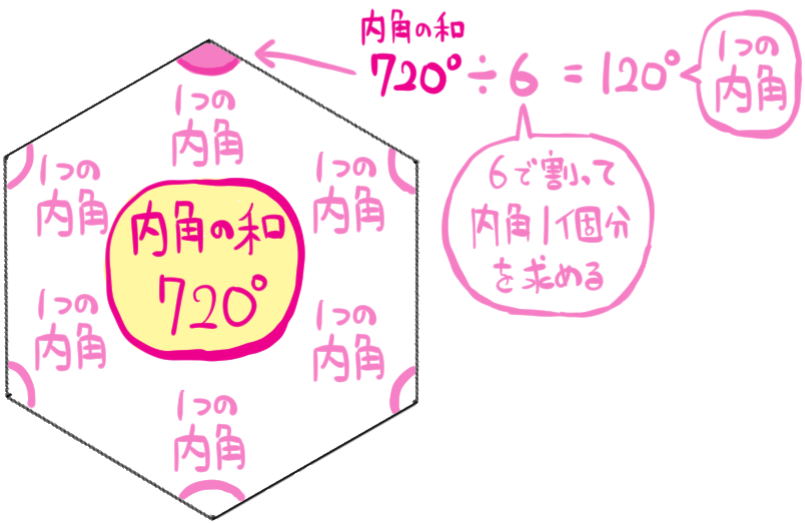正多角形の場合、すべての内角は同じ大きさをしています。
なので、内角の和を６で割ることで、内角一つ分の大きさを計算するということです。
坂田先生
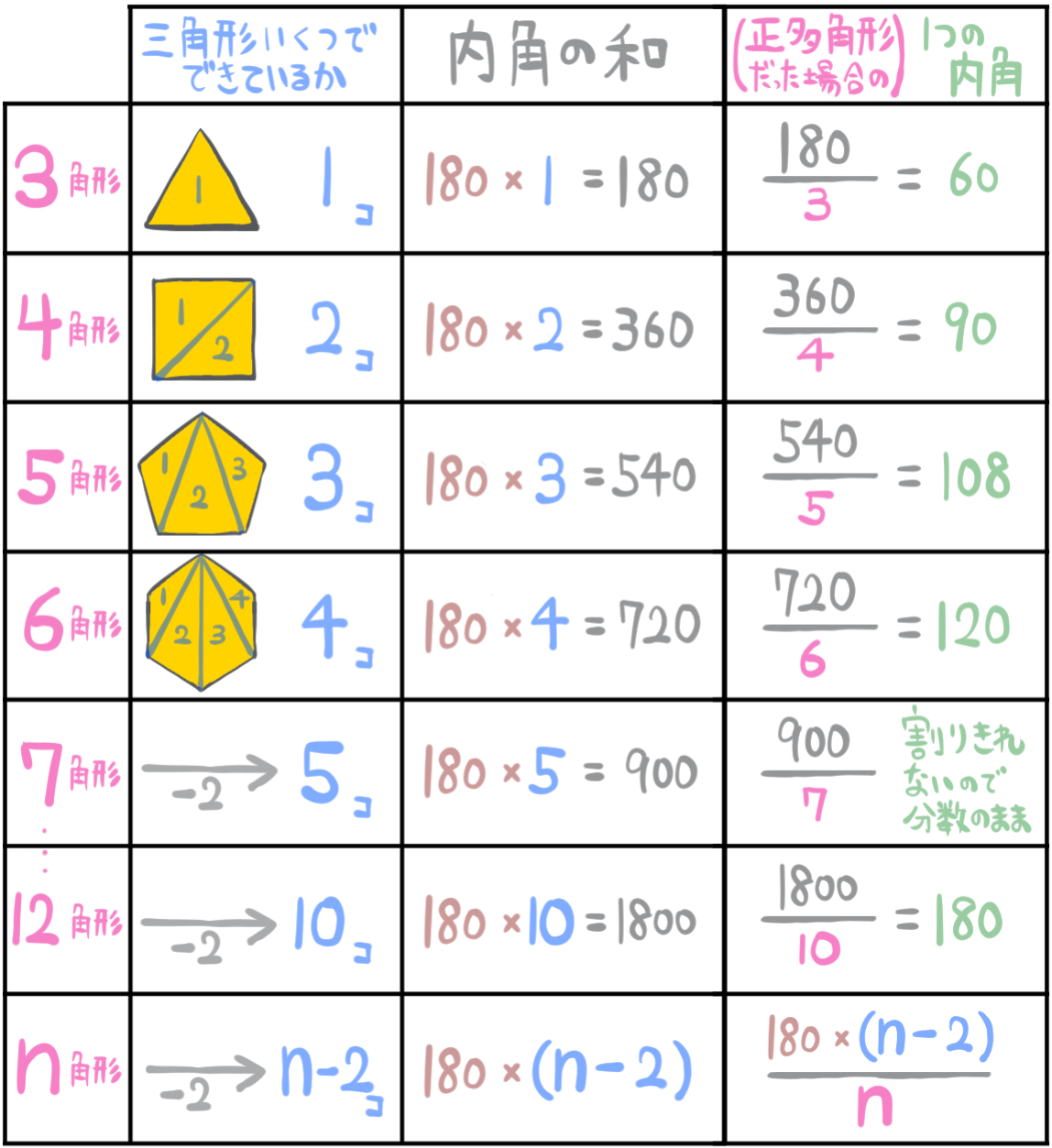
今の考え方を使って正多角形の内角一つ分の大きさを求める場合、一覧にすると以下のようになります。
にゃんこ
正ｎ角形の一つの内角を求める公式も、わざわざ覚えるまでもなく、ここまでの意味がわかっていれば、その場で作ることができます。
正六角形の一つの外角の求め方
坂田先生
最後は正六角形の一つの外角の求め方です。
にゃんこ
多角形の外角というのは、このようなもの↓です。
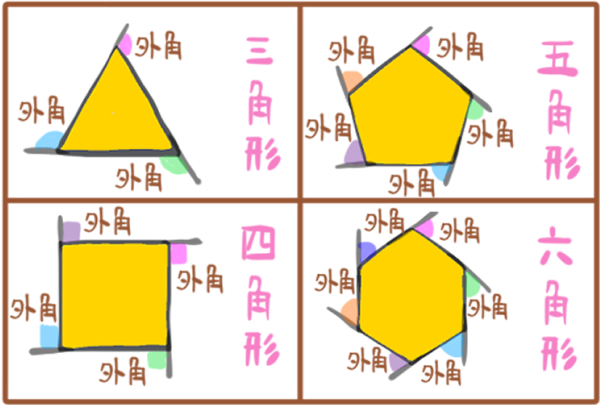
坂田先生
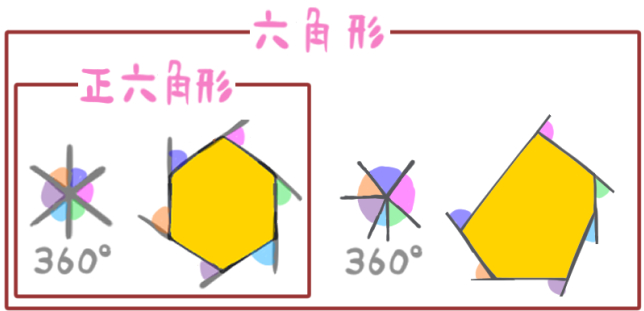
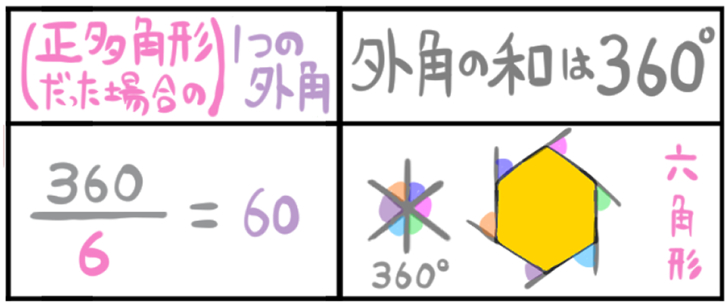
一つの多角形の外角を寄せ集めると、ちょうど円一周分、すなわち360°の大きさになります。
にゃんこ
これは、正六角形でも、六角形でも外角の和は360°になります。
坂田先生
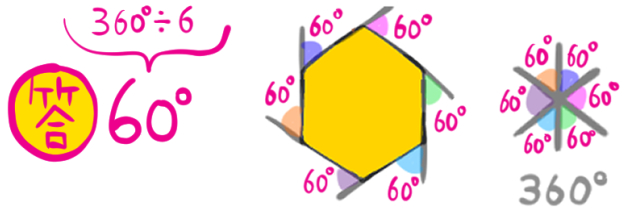
なので、一つの外角を求める問題は、以下のように解くことができます。
問題１
正六角形の一つの外角の大きさを求めよ。
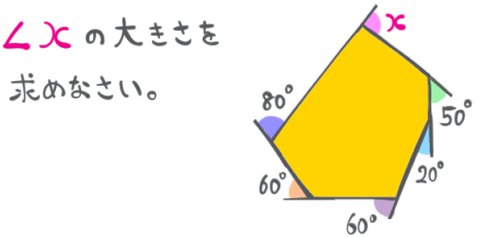
問題２
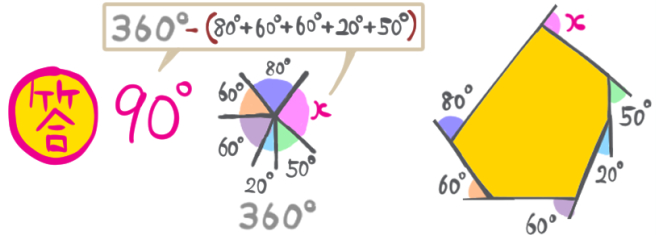
坂田先生
正六角形および六角形の外角について、まとめるとこうなります。
にゃんこ
六角形以外の外角についてはこのようになります。
正六角形の一つの外角と一つの内角の和は180°
多角形または正多角形の一つの外角と、その部分の一つの内角の合計は、常に180°になります。
例えば正六角形の一つの外角は60°で、一つの内角は120°でした。
一つの外角60°と一つの内角120°を合計すると180°になります。
坂田先生
このことを利用すると、問題によっては簡単に解くことができる場合があります。
\(180\left( 6-2\right) =180\times 4=720\)
または
\(180n-360\) のｎに６を代入して
\(180\times 6-360=1080-360=720\)