にゃんこ
一辺の長さから正六角形の面積を求める手順について、中学数学用に解説します。
このページの内容
- 正六角形の面積の求め方の公式｜内部の正三角形を６倍するおすすめ版
- 例題で習得｜公式を使わず正六角形の面積を求める方法
- 正六角形の面積の公式と覚え方｜語呂合わせ
正六角形の面積の求め方の公式｜内部の正三角形を６倍するおすすめ版
坂田先生
後半に紹介する、正六角形の面積を直接求める公式もありますが、それよりもこれから説明する方法で求めることをおすすめします。
にゃんこ
それは、正六角形の内部にある正三角形の面積の公式を覚えて、それを６倍する、という方法です。
坂田先生
一辺の長さをaとする正六角形で見てみましょう。
このように、正六角形の面積は、正六角形の対角線によってできる内部の正三角形の面積を６倍した大きさになります。
坂田先生
これ↓がズバリ結論です。
この方法をおすすめする理由は、そもそも三平方の定理の分野にて、『正三角形の１辺の長さから面積を求めさせる問題』というのは公式を覚えておいてもいいくらい頻繁に登場するからです。
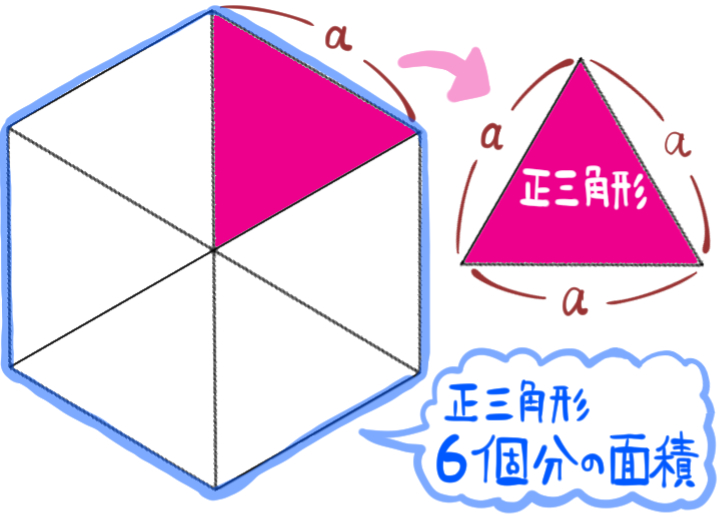
あとはそれを６倍すればいいだけなのだから、何も正六角形の面積の公式まで覚えるのは、無駄の多い作業と言っていいでしょう。
坂田先生
正三角形の面積を求める過程を以下に説明しますが、これは同時に、公式を使わないで正六角形の１辺の長さから面積を求めていく手順と、同じ内容になります。
にゃんこ
三平方の定理の分野で重要な考え方なので、公式を覚えるだけでなく、しっかりと理解しておくといいでしょう。
一辺の長さから正六角形の面積を導く手順
坂田先生
一辺の長さがaの正六角形の面積を求める手順を解説します。
にゃんこ
まずは、この正三角形の高さを求めます。
坂田先生
特別な直角三角形の三辺の長さの比、を覚えておいて、それを利用します。
特別な直角三角形というのは、三角定規の形として使われている直角三角形のことです。
30°、60°、90°の直角三角形は、辺の長さの比が1:2: \(\sqrt{3}\)(約1.7) になっています。（一番長いななめの長さの比が2にあたります）
にゃんこ
これを利用して比例式を作って『高さ』にあたる部分の長さを求めます。
坂田先生
また、このような求め方もあります。（辺の比を利用した考え方です）
にゃんこ
『高さ』がわかったら、次は正三角形の面積を求めます。
1辺がaの正三角形の面積の公式
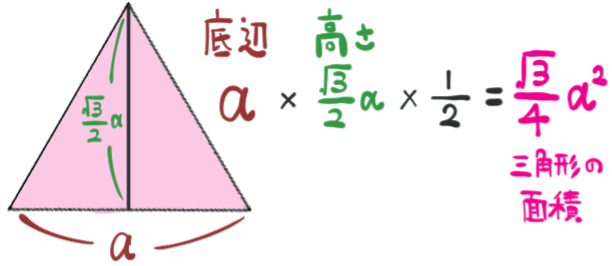
\(\dfrac{\sqrt{3}}{4}a^{2}\)
坂田先生
最後にこれを６倍すると正六角形の面積が求まります。
にゃんこ
ここまでの流れが、一辺の長さから正六角形の面積を導く手順の説明になります。
坂田先生
次に、この手順をマネして、公式を使わないで正六角形の面積を求める練習をします。
例題で習得｜公式を使わず正六角形の面積を求める方法
つづいてこちらの例題にて、公式を使わないで正六角形の面積を求めていきます。
問題
一辺の長さが５の正六角形の面積を求めよ。
まず、正六角形の面積は、次のように正六角形内部にある正三角形の面積６個分の大きさなんだな、と考えます。
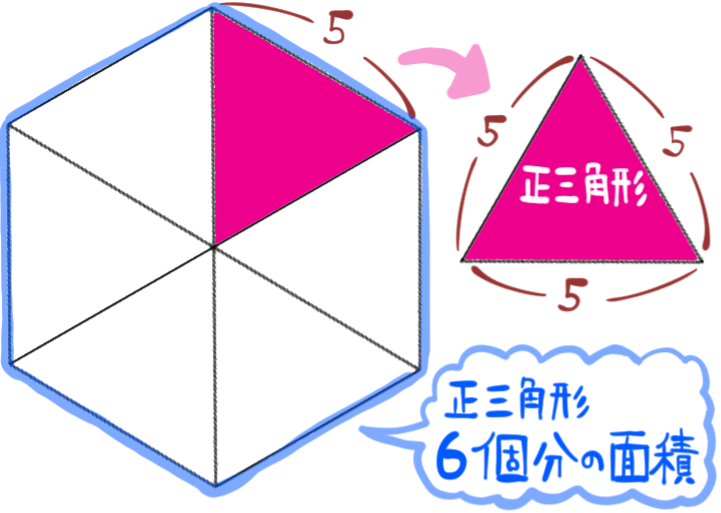
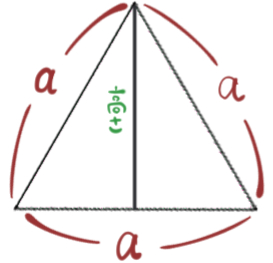
次に、その１辺が５の正三角形を取り出して、高さを求める方法、を考えます。
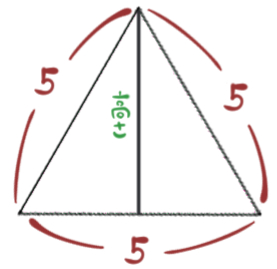
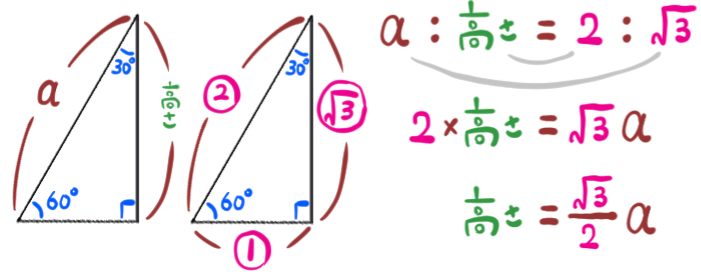
正三角形を左右に二分割すると、三角定規でおなじみの特別な直角三角形の形が表れます。
この辺の長さの比は決まっているので、それを利用します。
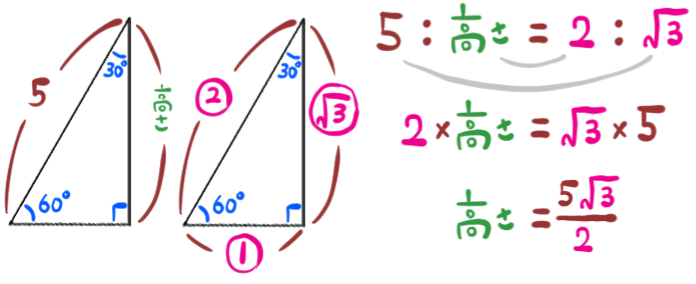
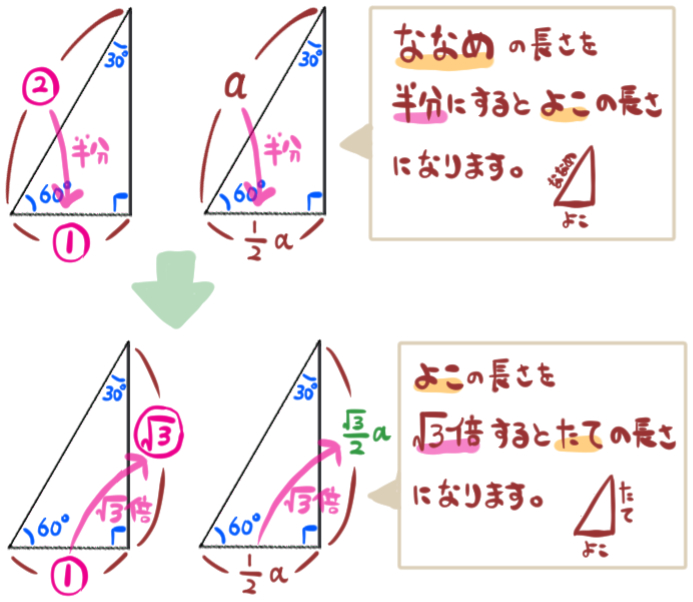
また、こちらの方法でも求めることができます。
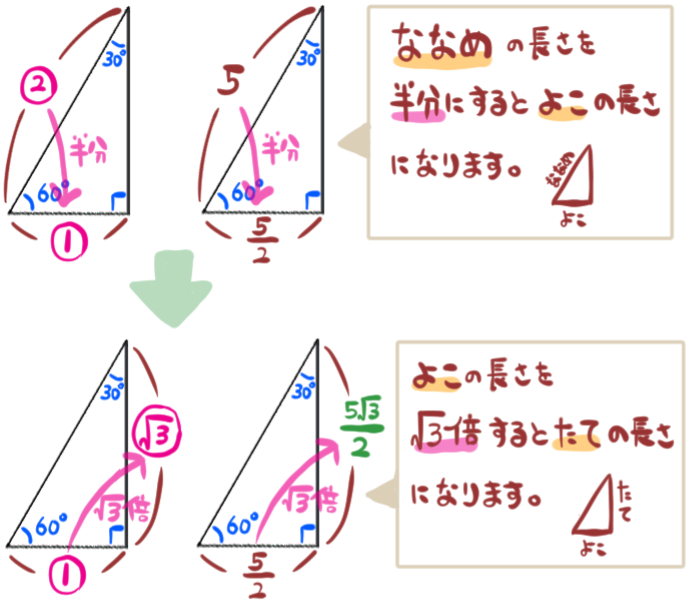
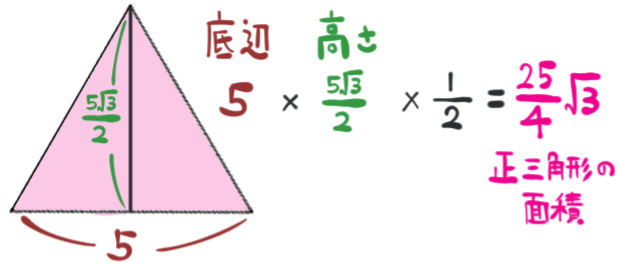
高さが求められたら、次に正三角形の面積を求めます。
最後に、その６個分の面積を求めて、正六角形の面積が求まります。
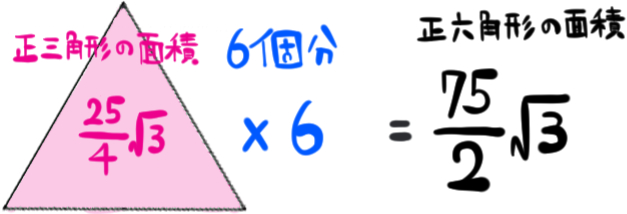
正六角形の面積の公式と覚え方｜語呂合わせ
坂田先生
最後に、正六角形の面積の公式を一応、ここにまとめておきます。
にゃんこ
最初に説明したように、正三角形の面積の公式を覚えて、それを６倍する方法をおすすめします。
１辺の長さをaとおくと正六角形の面積はこのような公式になります。
\(\dfrac{3\sqrt{3}}{2}a^{2}\)
\(\dfrac{3\sqrt{3}}{2}\)×１辺×１辺
でもいいです。
語呂合わせによる覚え方
ロックバンドを指さして「二人分の耳、変だよ！変！」
と覚えるといいでしょう。
ロックは六角形のロクです。
二人分の（２分の）
耳（\(3\sqrt{3}\) ）
変だよ(一辺)変(一辺)
という語呂合わせです。
ロックバンドのライブに来ていたファンの一人が、舞台上で熱狂している２人があまりにもノリノリすぎて耳から煙が出ているのを発見し、思わず我が目を疑った。
‥という絵を思い浮かべてください。
にゃんこ
二人分の耳、変だよ！変！
にゃんこ
または次のようなかたちでも同じです。
正六角形の面積の公式
- \(\dfrac{１辺×１辺\times 3\sqrt{3}}{2}\)
- １辺×１辺× \(\dfrac{3\sqrt{3}}{2}\)
- １辺×１辺× \(3\sqrt{3}\times \dfrac{1}{2}\)
- １辺×１辺× \(3\times \sqrt{3}\div 2\)
にゃんこ
【お願い】万が一、間違いを発見された方は、こちらまで連絡をいただけると非常に助かりますm(__)m
