

にゃんこ
このページでは、座標平面上にある線分の垂直二等分線の式の求め方と公式について解説します。
このページの内容
- 線分の垂直二等分線の求め方|例題で解説
- 線分の垂直二等分線の公式
・傾きの公式
・y切片の公式
・垂直二等分線の公式
合わせて学習したい一次関数
参考:2点から等距離にある直線の式の求め方2通りと公式3つ
参考:3点から等距離にある点の座標の求め方3通り
参考:3点を頂点とする三角形の面積を求める公式|原点を通る場合通らない場合
線分の垂直二等分線の求め方|例題で解説
例題
次の線分ABの垂直二等分線を求めなさい。
2点A,Bの座標はそれぞれA(1,5)、B(7,9)とする。
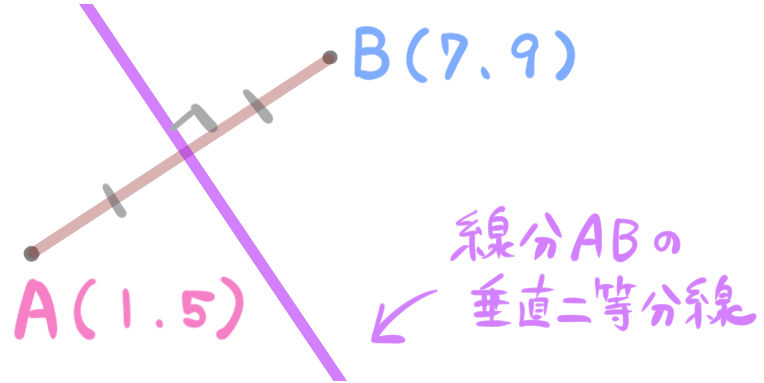
手順1:直線ABの傾きを求める

坂田先生
2点A,Bの座標がわかっているので、直線ABの傾きを求めます。
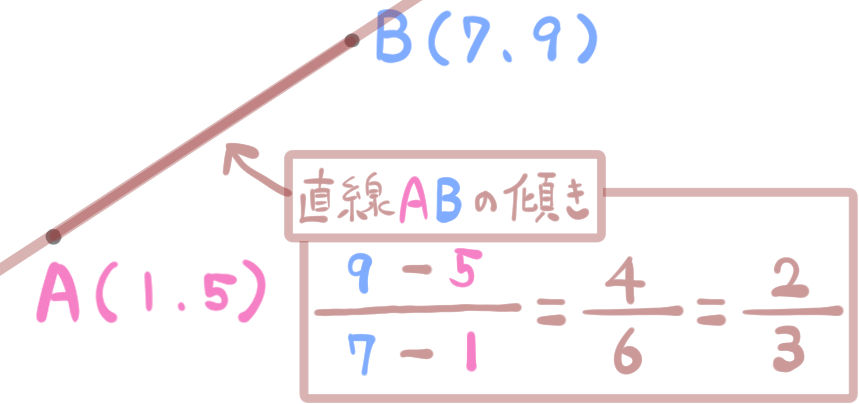

にゃんこ
これによって求めた直線ABの傾きは、次の手順にて、垂線の傾きを求めるために使います。
手順2:線分ABの垂線の傾きを求める

坂田先生
「直線ABの傾き」がわかったら、次は「線分ABに対して垂直に交わる直線の傾き」を求めます。

にゃんこ
結論から言いますと、「直線ABの傾き」の逆数かつ異符号が垂線の傾きになります。
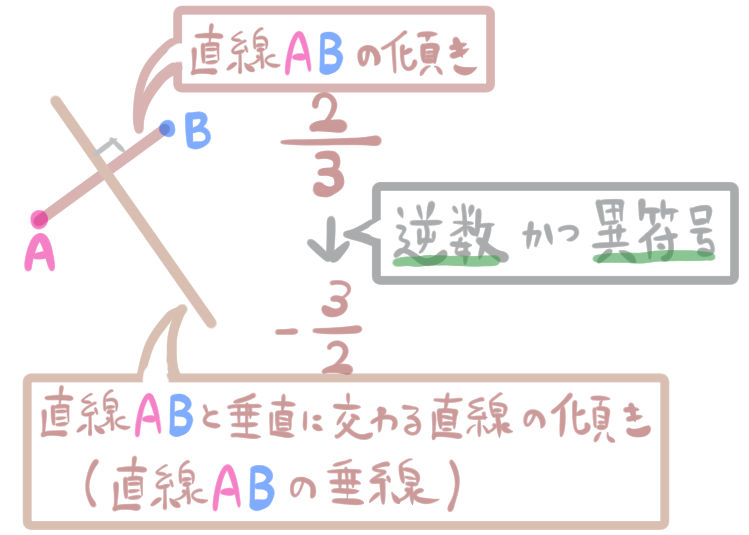

坂田先生
教科書などでは、「2直線が垂直に交わるとき、その2直線の傾きの積はマイナス1となる」といった説明がされています。

にゃんこ
それを簡単に使う方法が「逆数かつ異符号を求める」ということになります。

にゃんこ
垂線の傾きについてポイントをまとめておきます。
2直線が垂直に交わる場合の法則

坂田先生
確認してみると、次のようにちゃんと傾きの積がマイナス1になっていますね。
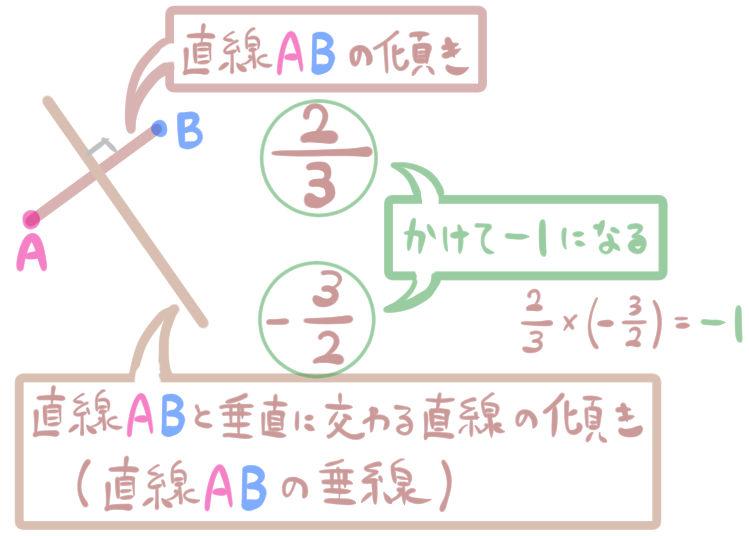

にゃんこ
線分ABの垂線の傾きがわかったということは、線分ABの垂線二等分線の傾きがわかったということです。
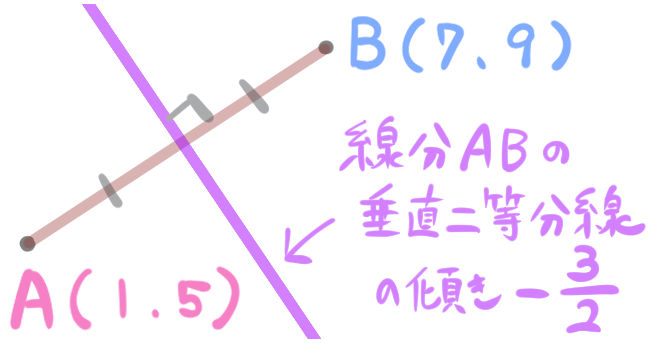
手順3:線分ABの中点の座標を求める

坂田先生
次に、線分ABの中点の座標を求めます。
中点のy座標は、2点A,Bのy座標の平均です。
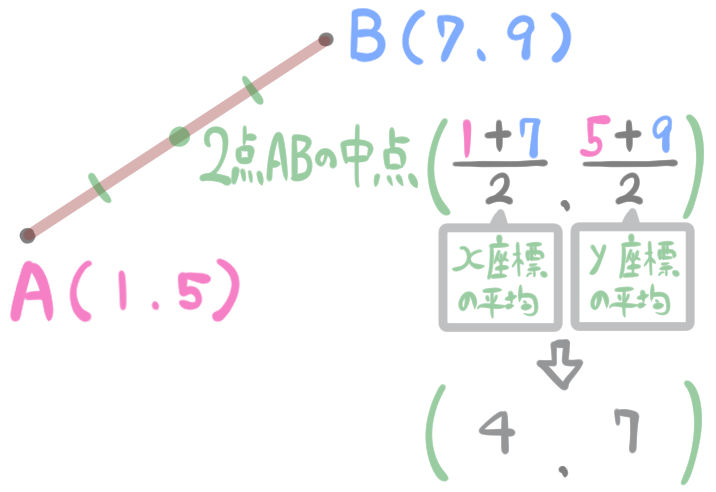

にゃんこ
これで下準備完了です。

坂田先生
ここまでの手順で、次の2つが準備できました。
準備できたこと
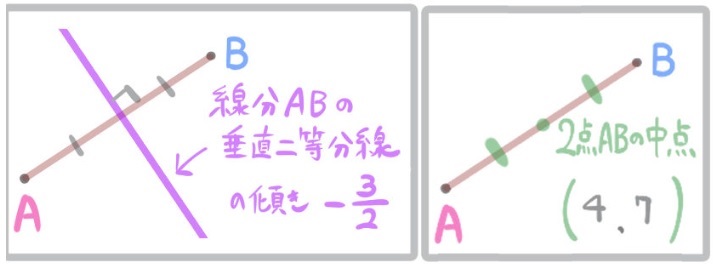
1:垂直二等分線の傾き(線分ABの垂線の傾き)
2:線分ABの中点の座標
このあと進める手順
求める垂直二等分線の傾きがわかったのだから、あとは垂直二等分線のy切片が判明すれば、式は完成ということになります。
そのために、『2:線分ABの中点の座標』を求めたということです。
次の手順で線分ABの中点のx座標とy座標を代入して、y切片を求めていきます。
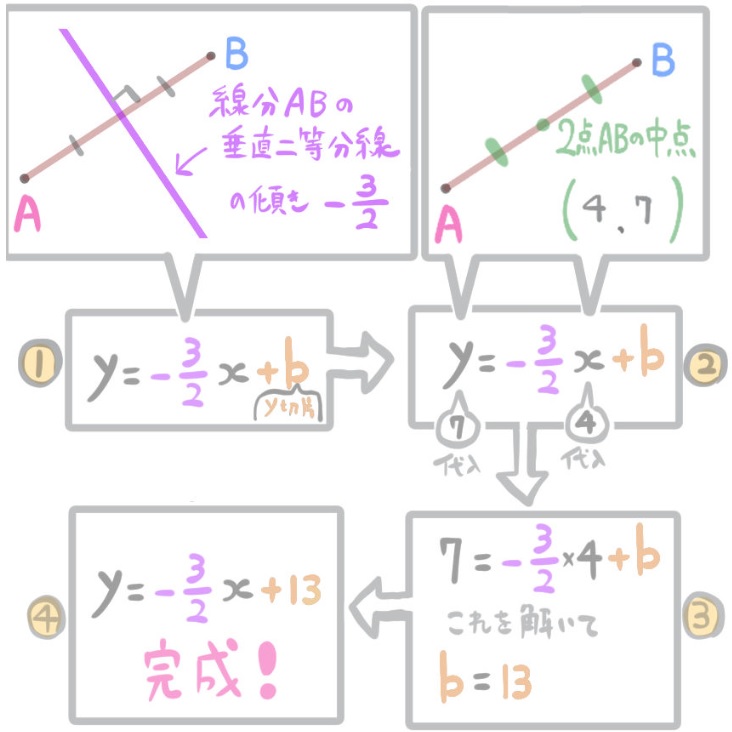
4つの手順
- 線分ABの垂直二等分線の傾きを代入し\(y=-\dfrac{3}{2}x+b\)を作る。
- 線分ABの中点のx座標y座標の値を\(y=-\dfrac{3}{2}x+b\)に代入する。
- この式をbについて解いてbの値、すなわちy切片の値を求める。
- 式が完成する。

にゃんこ
手順は以上です。

坂田先生
ここまでの線分の垂直二等分線を求める手順をまとめるとこうなります。
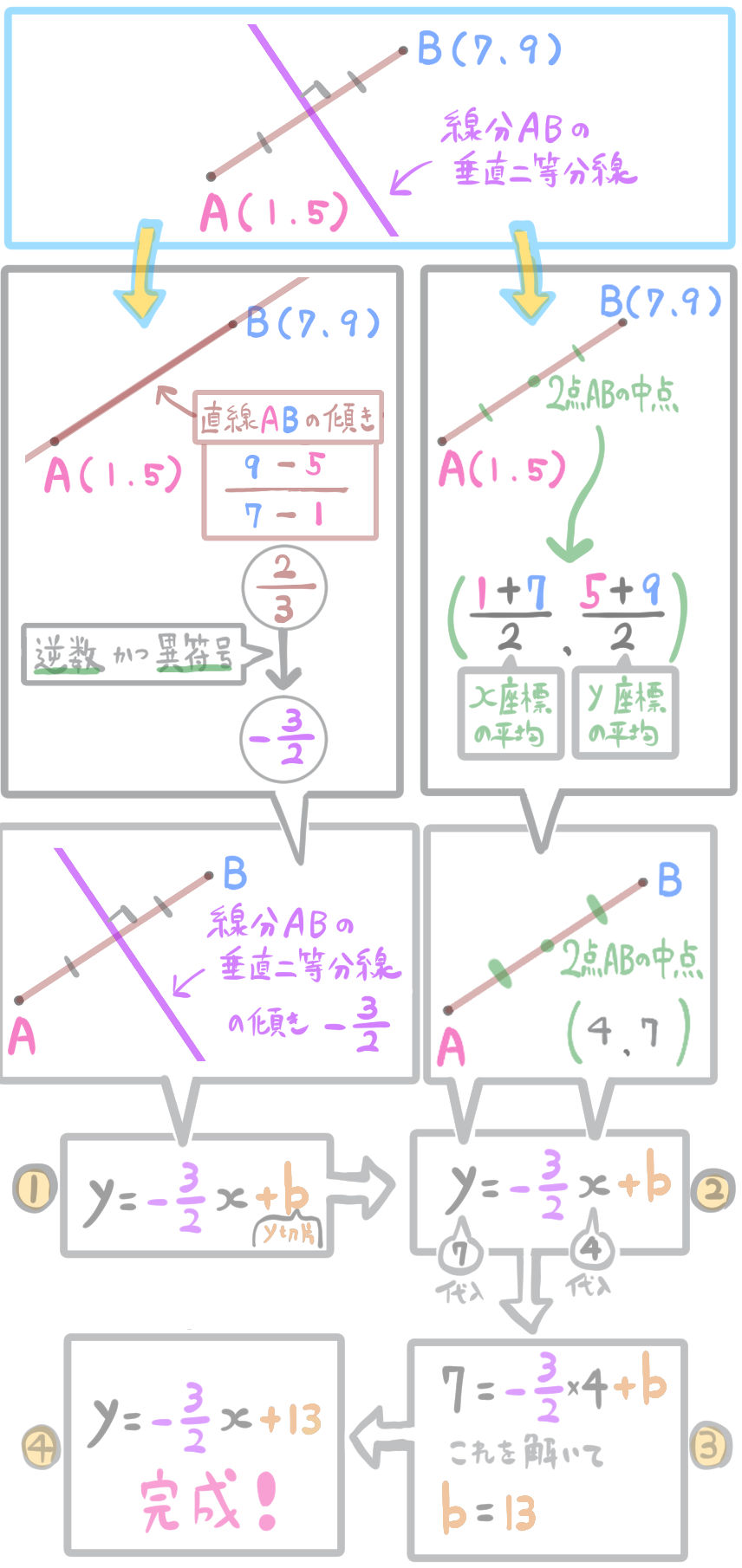
線分の垂直二等分線の公式

にゃんこ
次は、ここまでの手順と同じようにして公式を導いていきます。
次の線分の垂直二等分線の公式
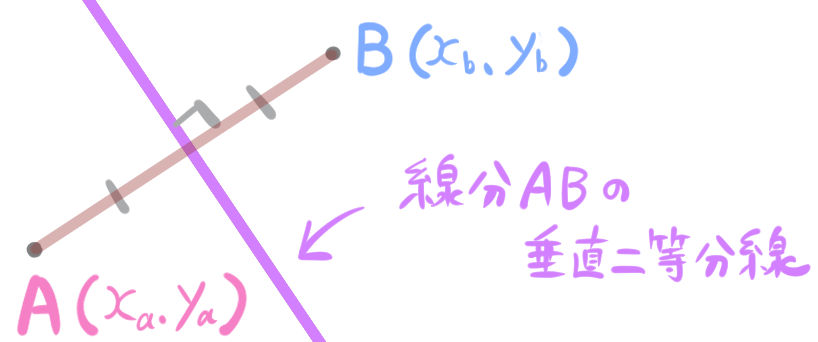

坂田先生
この公式を作ります。

にゃんこ
まずは傾きを求めていましたよね。
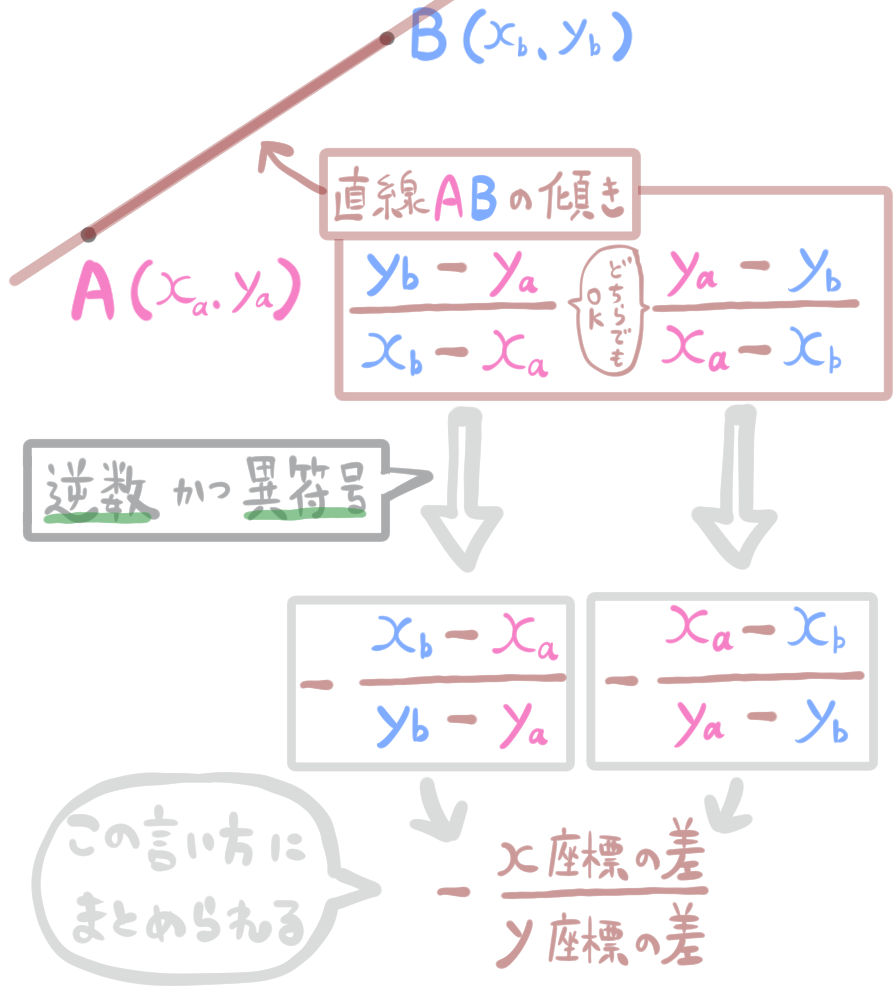
ここでの操作と結論
- 線分ABの傾きを求める。
- その傾きの逆数かつ異符号を求める。
- 【結論】線分の垂直二等分線の傾きは次のようになる。
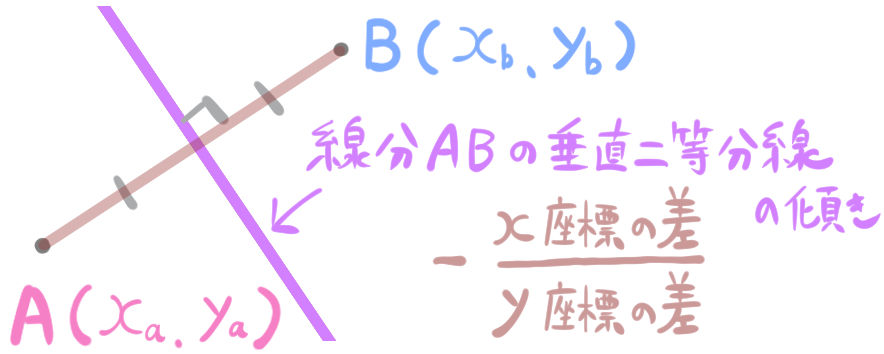

にゃんこ
ただしひとつ注意点↓があります。

中点の座標の一般化

坂田先生
続いて線分ABの中点の座標を一般化してみます。
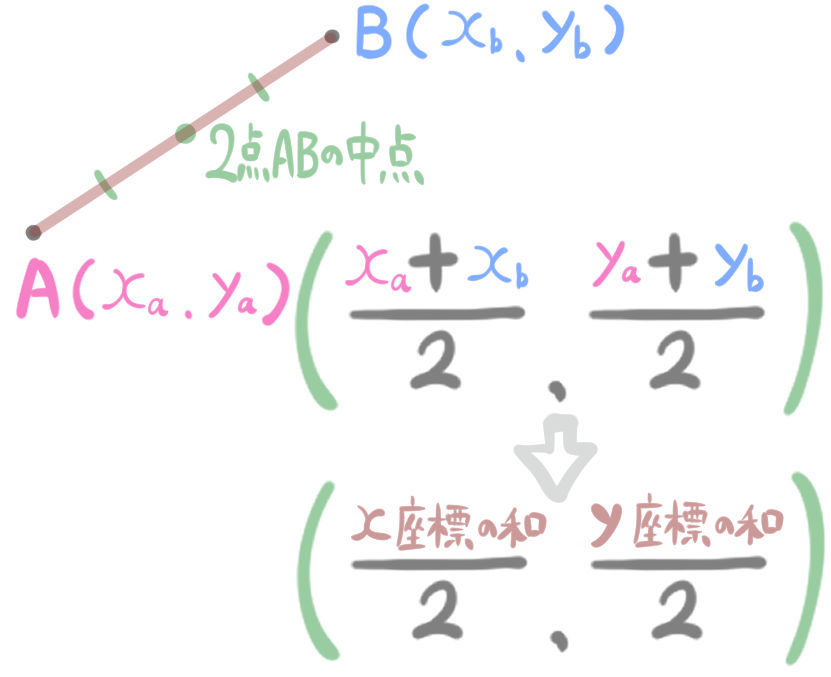

にゃんこ
このように最終的に「x座標の和」、「y座標の和」という言い方に変換しました。

坂田先生
「x座標の平均」、「y座標の平均」のかたまりで覚えたほうがスッキリするという方は、あとで紹介する公式をそのように書き直してみてください。
垂直二等分線の切片の公式を導きます。

坂田先生
求める直線の式(線分ABの垂直二等分線の式)を\(y=ax+b\)としたときの、bの値(y切片)を求める公式を作ります。

にゃんこ
例題で取り組んだように、線分ABの中点のx座標、y座標の値をこの式に代入して変形します。
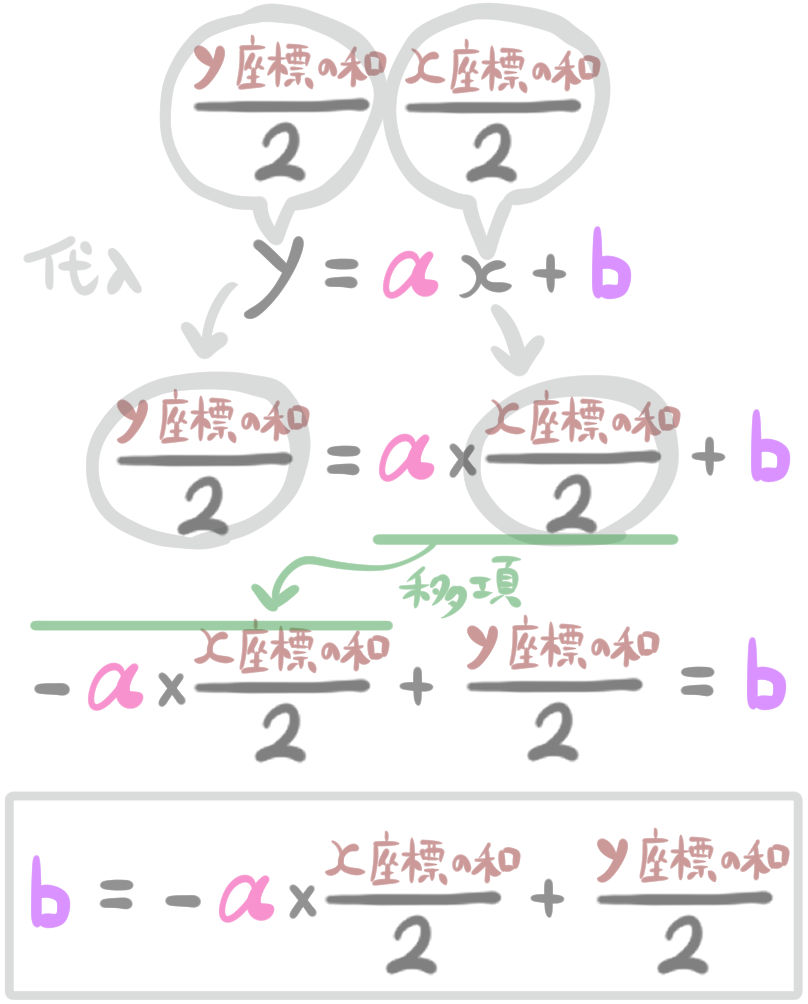

にゃんこ
これが切片の公式です。
線分の垂直二等分線の傾きと切片の公式
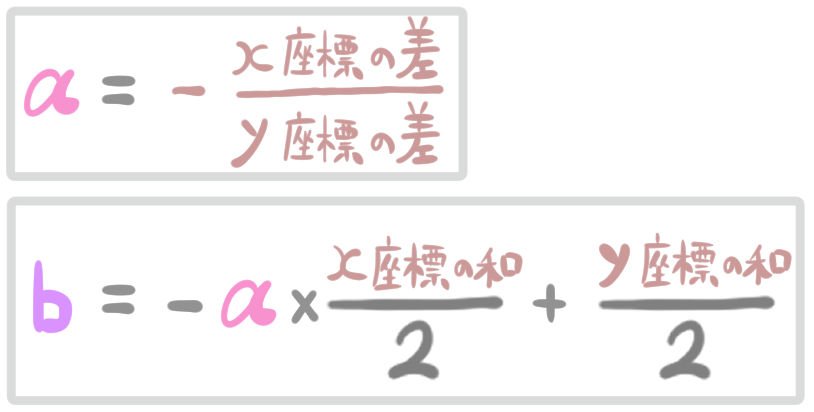

坂田先生
線分の垂直二等分線の式の公式をまとめるとこうなります。
公式まとめ
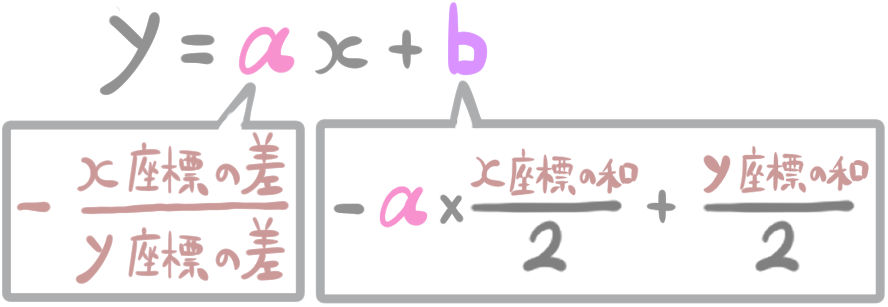

にゃんこ
後半の部分は「x座標の平均」、「y座標の平均」という言い方に直したほうが、よりスッキリして見やすいかもしれません。
合わせて学習したい一次関数
参考:2点から等距離にある直線の式の求め方2通りと公式3つ
参考:3点から等距離にある点の座標の求め方3通り
参考:3点を頂点とする三角形の面積を求める公式|原点を通る場合通らない場合





























・2直線が垂直に交わるとき、一方の傾きの逆数かつ異符号が、もう一方の傾きとなる。