

- 正六角形の対角線の長さの求め方
- 正六角形の対角線の本数の求め方|中学生用
- 【別解】 \(_6 C _2-6\)の式の意味|中学生用に解説
数Aの組み合わせによる求め方の式の意味を、Cを使わないで計算できるように、中学生にも意味がわかるように解説します。
正六角形の対角線の種類|長い方3本と短い方6本






正六角形の対角線の長さの求め方

長い方の対角線の長さの計算

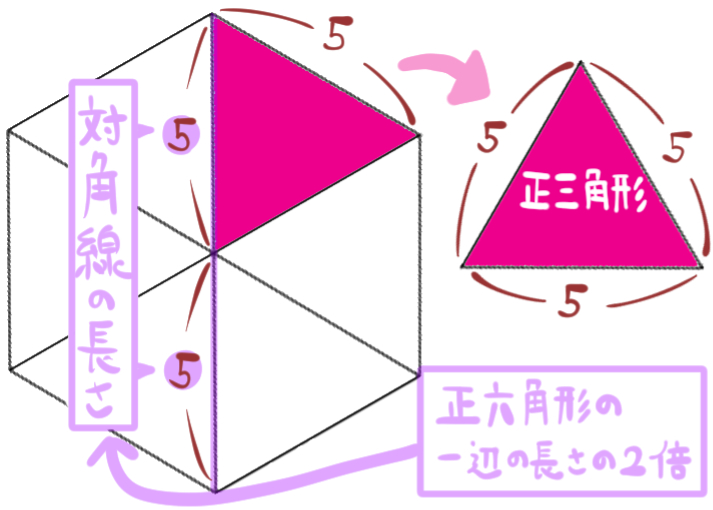



答:2a
短い方の対角線の長さの計算



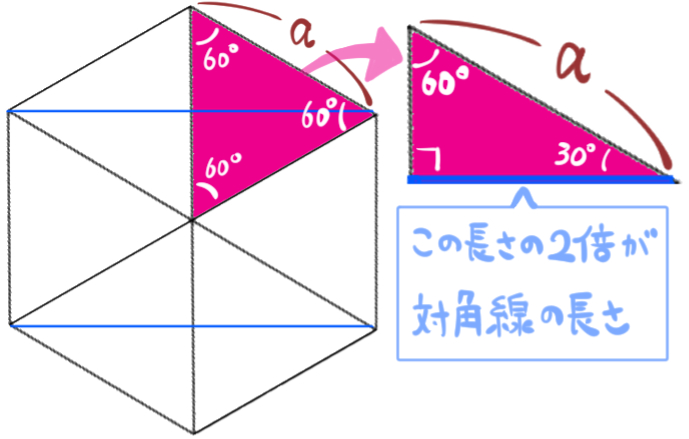



1つ目は、特別な直角三角形の辺の比を利用するという方法です。
このように計算します。
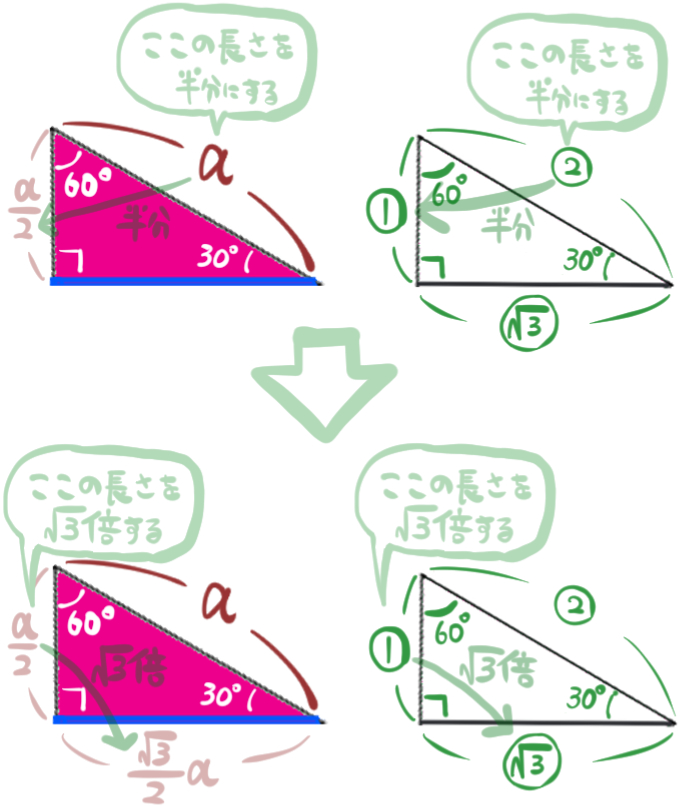
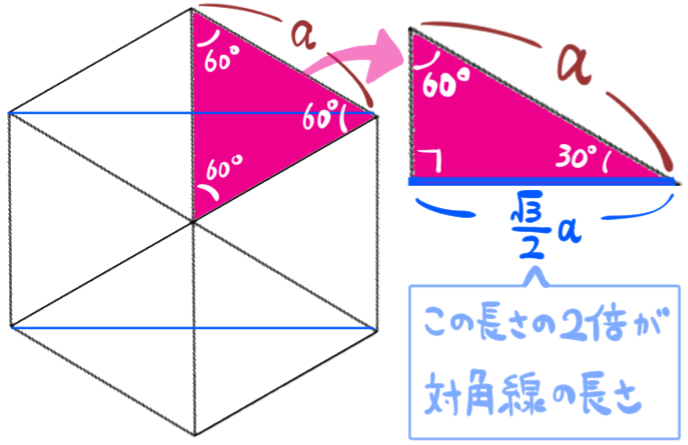
三角定規でよく見る形、すなわち30°、60°、90°の直角三角形の形が登場した場合、その辺の長さの比は図の右側のようになります。
縦の長さはななめの長さを半分にした長さなので、ななめの長さであるaを半分にした \(\dfrac{a}{2}\) が縦の長さになります。

続いて縦の長さを \(\sqrt{3}\)倍した長さが、横の長さになりますので、\(\dfrac{a}{2}\)を \(\sqrt{3}\)倍した \(\dfrac{\sqrt{3}}{2}a\) が、横の長さということになります。
これが1つ目の方法です。
2つ目の方法は、比例式を作って求める方法です。
求める青い太線部分の長さを?とおくと、特別な直角三角形(30°、60°、90°の形)の辺の長さの比と見比べて、次のように比例式を作ることができます。
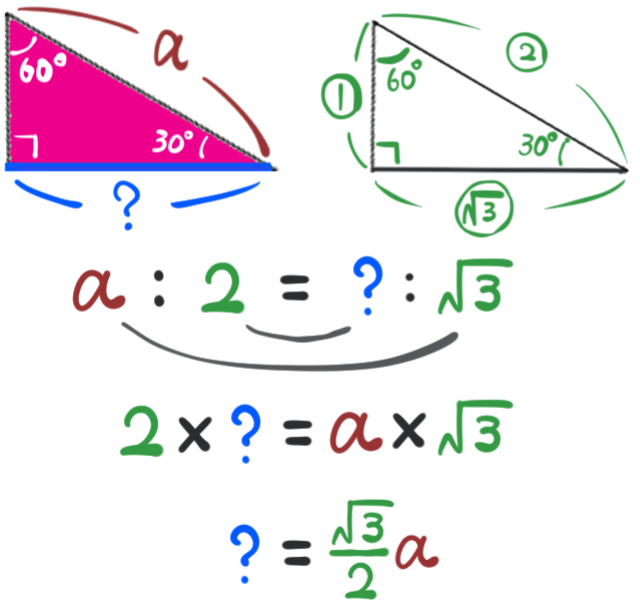
この比例式を?について解いて、?の部分の長さが\(\dfrac{\sqrt{3}}{2}a\) だということがわかりました。
(※ただし、試験で実際に使う場合は?ではなくて \(x\) などといった文字を使ってください。)


例えばaの部分が7だったらとしたら、このような計算で青い太字部分の長さを求めますね。
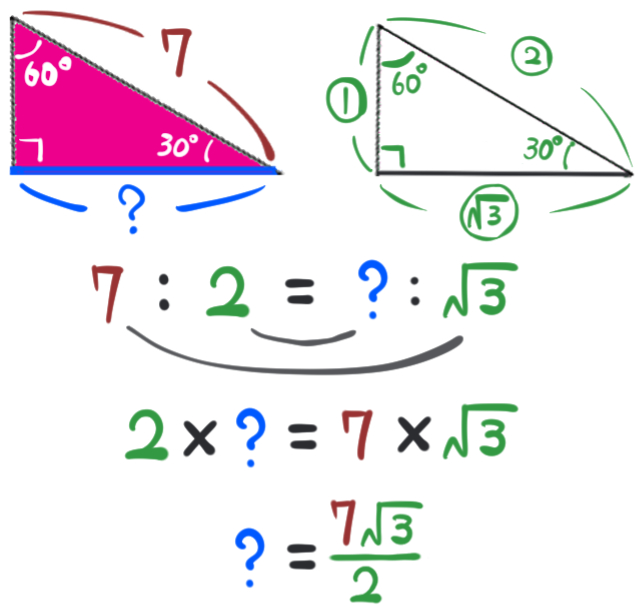


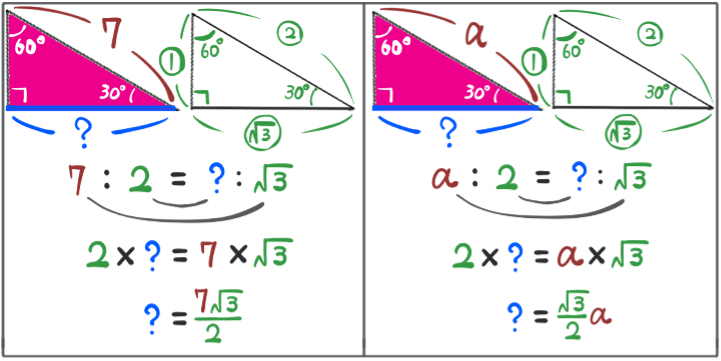
aの場合も7の場合も同じ手順で青い太字部分の長さを求めているということがわかるかと思います。
7の場合は、青い太字部分の長さが具体的な値としてちゃんとわかります。
それに対してaの場合は、青い太字部分の長さはaを使った式でしか表すことができない、ということですね。




答: \(7\sqrt{3}\)

正六角形の対角線の本数の求め方|中学生用
式: \(6\times \left( 6-3\right) \times \dfrac{1}{2}=9\)
別解: \(\dfrac{6\times 5}{2}-6=9\)←後で説明します
答:9本


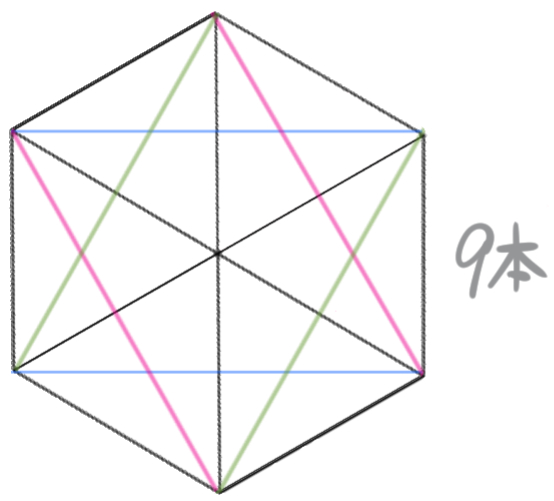
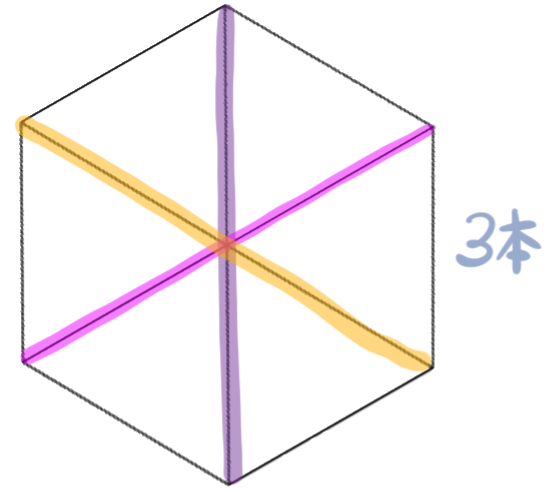
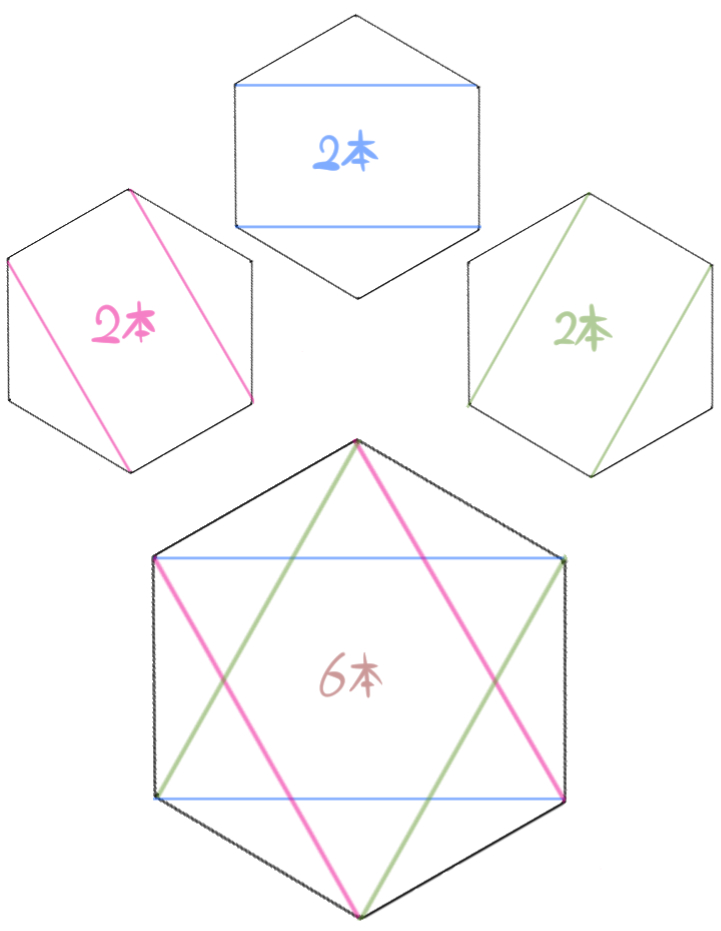
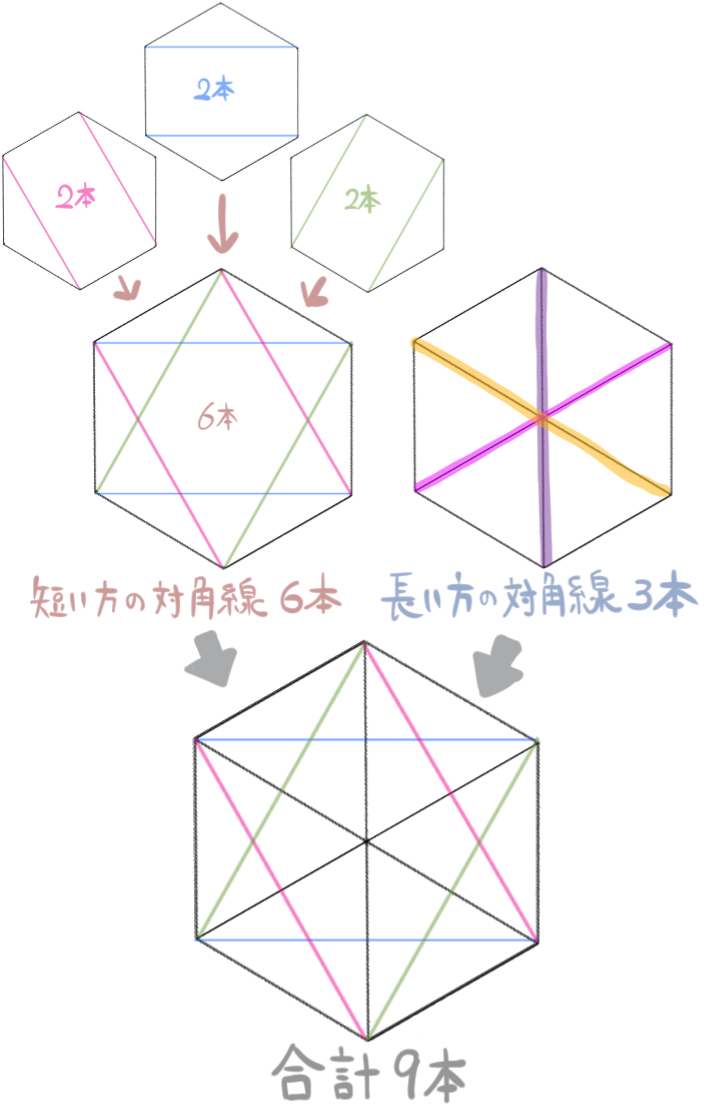
図のように、正六角形の対角線の本数は全部で9本ありました。(長い方が3本、短い方が6本)
これを場合の数の考え方によって、対角線の引き方が何通りできるか、という視点で求めてみます。

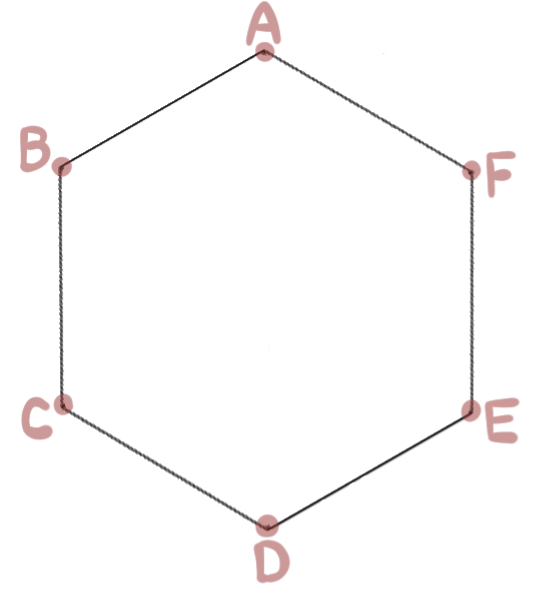
なので、6つの頂点のうちから2つを選ぶ組み合わせは何通りあるのか、ということを考えることになります。(ただし、あとで説明しますが注意点があります。)
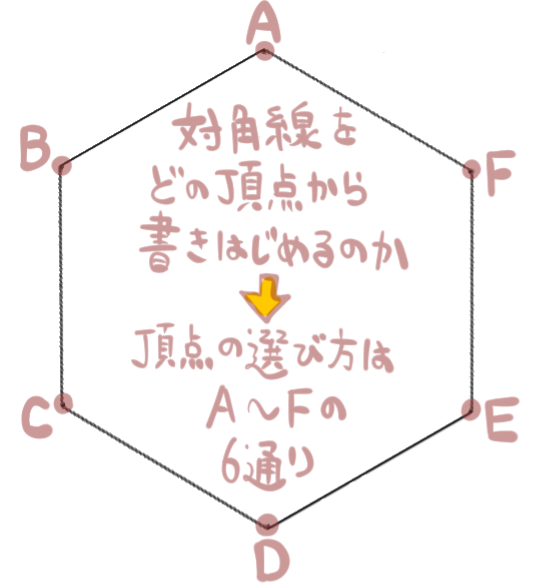
対角線を引き始める出発点の決め方はA~Fの6通りあります。

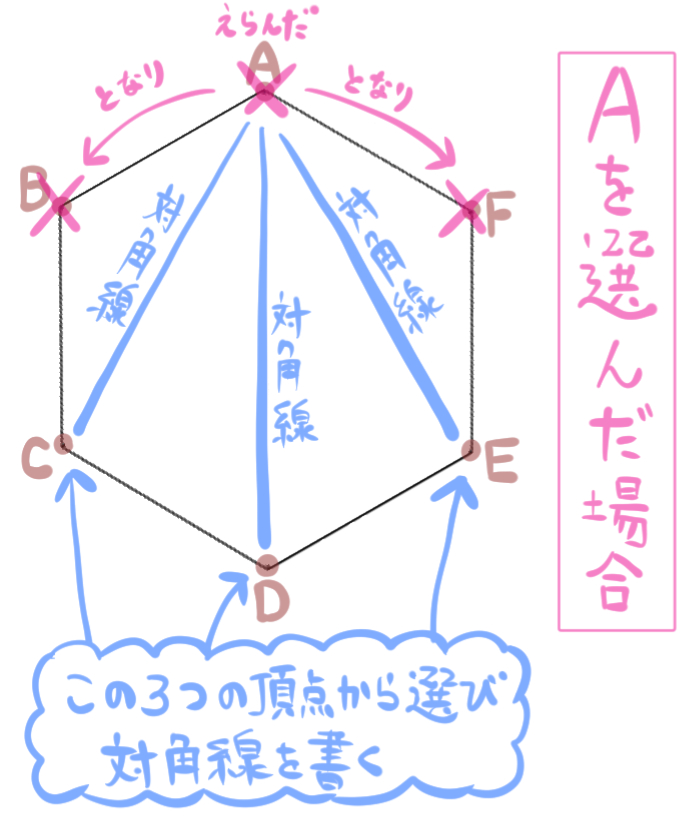
Aを選んだ場合は、ゴールの点としてAはもう選べないですね。
さらにAの両どなりにある、BやFも選べないことになります。
なぜかと言うと、例えばゴールの点としてBを選んだ場合「AとBを結ぶ線を引く」ことになります。
AとBを結ぶ線を引いたとしても、その線は正六角形の辺ABの線になりますよね。辺ABの線は対角線ではありません。
ゴールの点としてFを選んだ場合も同じように、対角線になりません。
結局ゴールの点として選べるのは、A~F6つあるうちのA、B、Fの3つを取り除いたC、D、Eの3通りしかない、ということになります。
対角線を書き始める点としてAを選んだ場合は、対角線の引き方はこの3通りということになります。


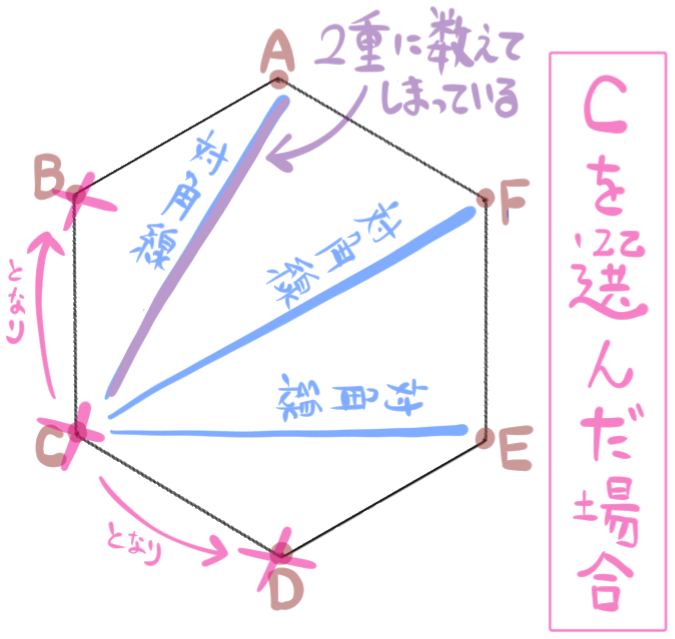
これは、対角線を書き始める点としてCを選んだ場合です。
この場合もゴールの点として選べるのは3通りあります。
対角線ACに注目してください。
これは、さっき対角線を書き始める点としてAを選んだ場合にカウントしたもののなかに入っていますね。

つまり2重に数えてしまうことになります。
この余計に数えてしまう部分をどうするか、について次の樹形図で説明します。
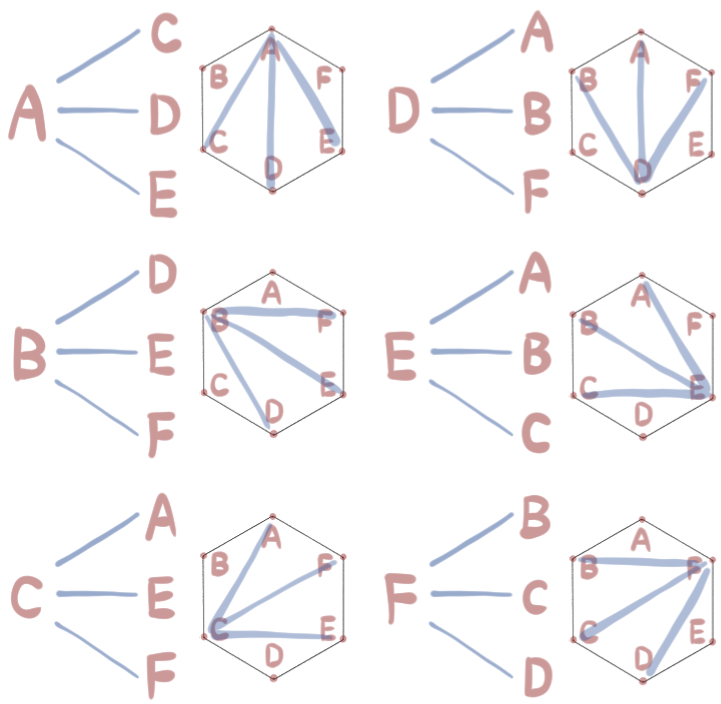
とりあえず、2重に数えてもいいから、さっきの方法で全部で何通りあるかを計算します。
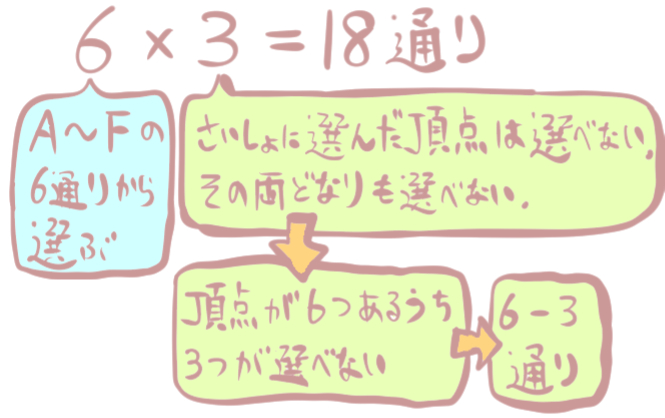
このように、2重カウントを含めて計算すると、18通りの対角線の引き方があるという結果になりました。
では次に、2重に数えてしまっているのは18通りのうちどれだけあるのか、について見ていきます。
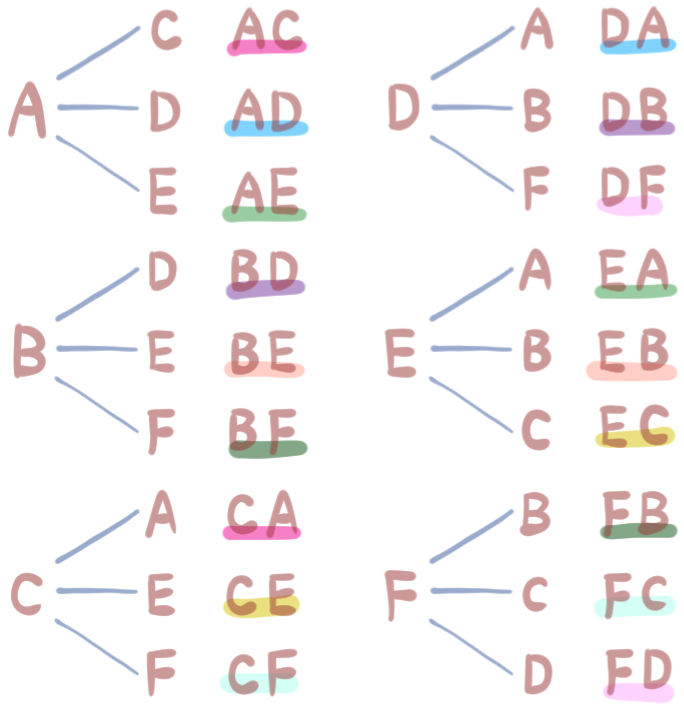
上の表で、同じ対角線にあたるものは、同じ色で下線を引いています。
例えば、ABとBAの部分は同じ対角線ですね。
BEとEBも同じ対角線です。
このように、前後の文字を入れ替えたものはすべて2重に数えてしまっているということになります。
同じ色で下線を引いているものは、同じ対角線なので、その片方を消してみます。
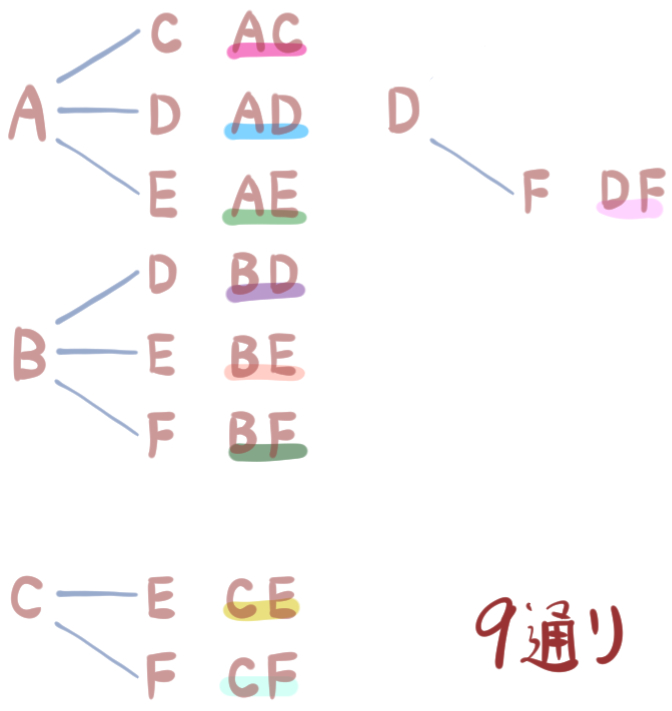
そうすると、18通りあったものが、9通りだけになりました。
結局、本来の2倍数えてしまっていたということです。

上の計算ではダブりを含めて2倍数えていたということですね。
なので最後にそれを半分にして、計算を仕上げます。
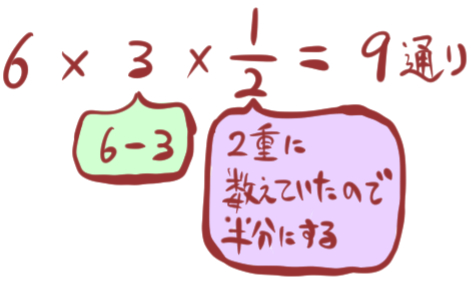
式: \(6\times \left( 6-3\right) \times \dfrac{1}{2}=9\)
答:9本

この30通りは、本来の2倍カウントしてしまっているので、30の半分である15本が求める数となる。

【別解】 \(_6 C _2-6\)の式の意味|中学生用に解説

(中学生用)式: \(\dfrac{6\times 5}{2}-6=9\)
(高校生用)式: \(_6 C _2-6=9\)
※この2つの式は同じ内容になっています。
答:9本


対角線をA~Fのどの頂点から引き始めるかが6通り
スタートの点としてAを選んだ場合、ゴールの点の選び方はC、D、Fの3通り
このように考えて、6×3の18通り
だけど、本来の倍をカウントしていることになるので、対角線の本数はその半分で9本
ということでしたね。




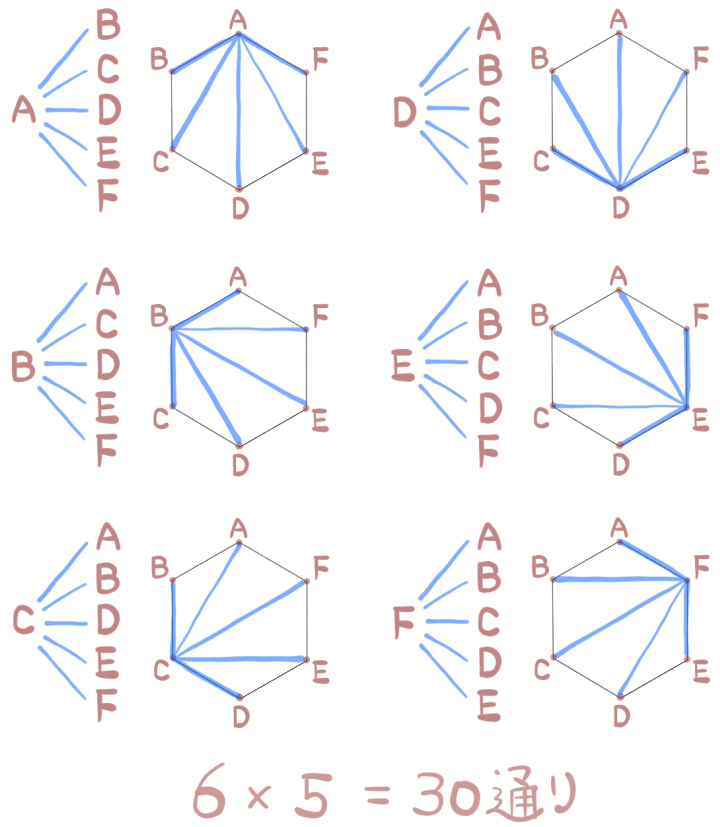
例えばAを選んだ場合、次に選ぶのはA以外の5通り
最初にA以外を選んだ場合も、次に選ぶのは5通り
よって6×5の30通り
‥となります。
ただしこれも、本来の2倍を数えてしまっているので、2重にカウントしている分を消すと、こうなります。
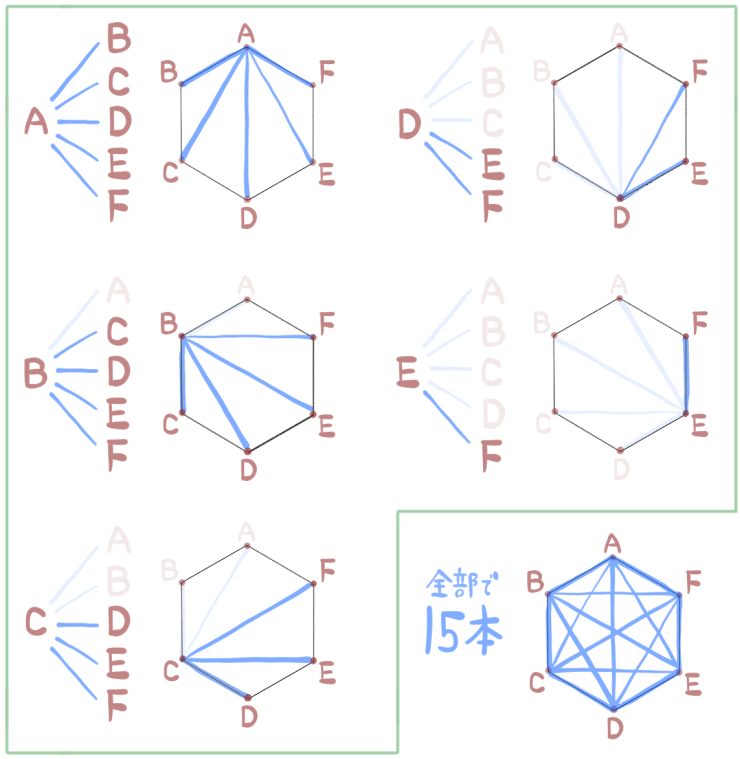
この15本は、正六角形の辺の数と対角線の数を合計したものになっています。
なので、そこから辺の数である6を引くと、対角線の本数だけが求まります。
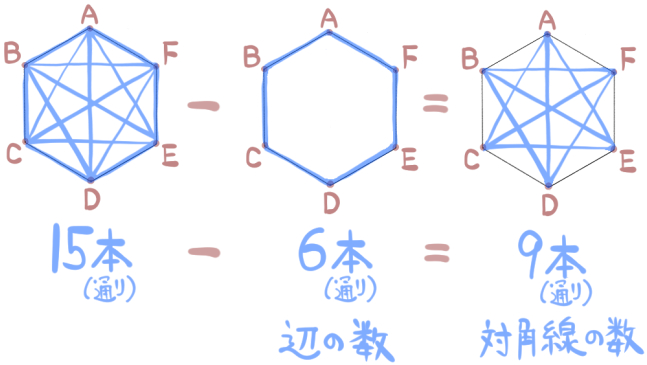

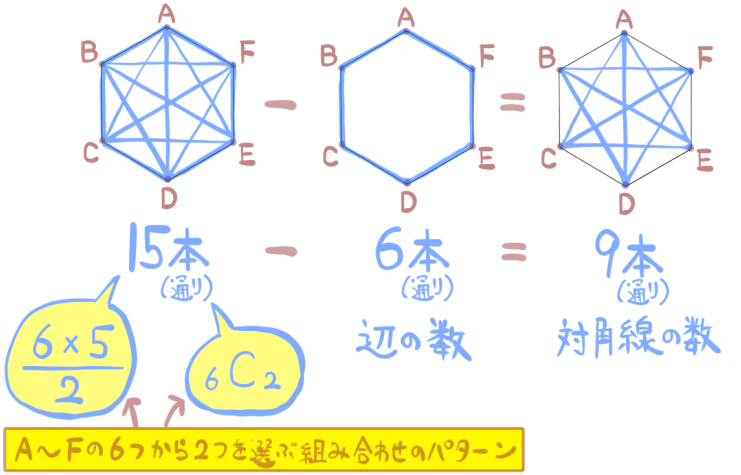

ステップ2:15本のうち、6本が正六角形の辺になっているから、その分を引いてあげて、9本が対角線の本数となる。
































