- 面積比の求め方｜底辺または高さのどちらかが違う図形の場合
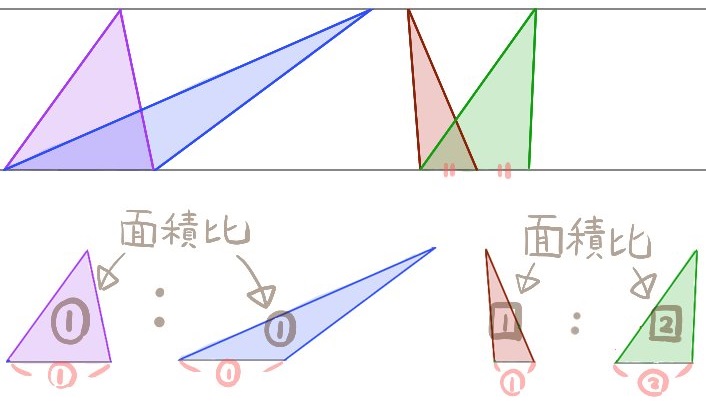
- 平行線と三角形の面積比
- 三角形の面積を二等分する直線の方程式
- 角の二等分線と面積比
- 相似比を使った面積比の求め方
- ３つの三角形の面積比の問題
- 座標平面上の三角形の面積比を扱うテクニック
- 【復習用】平行四辺形における面積比の問題
面積比の求め方｜底辺または高さのどちらかが違う図形の場合
底辺の長さが等しい場合、２つの図形の面積比は高さの比と同じになります。
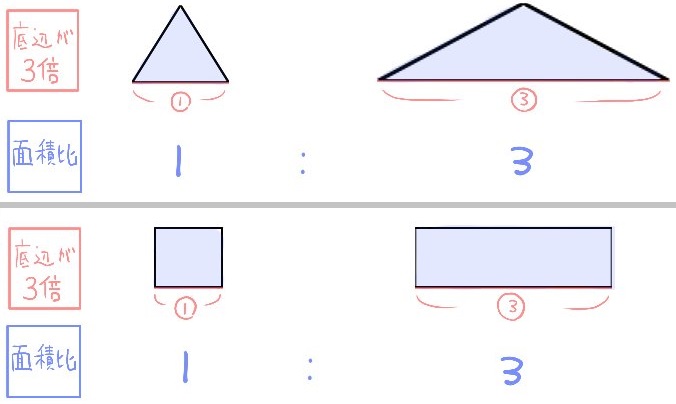高さが等しい２つの図形の場合、面積比は底辺の長さの比と同じになります。
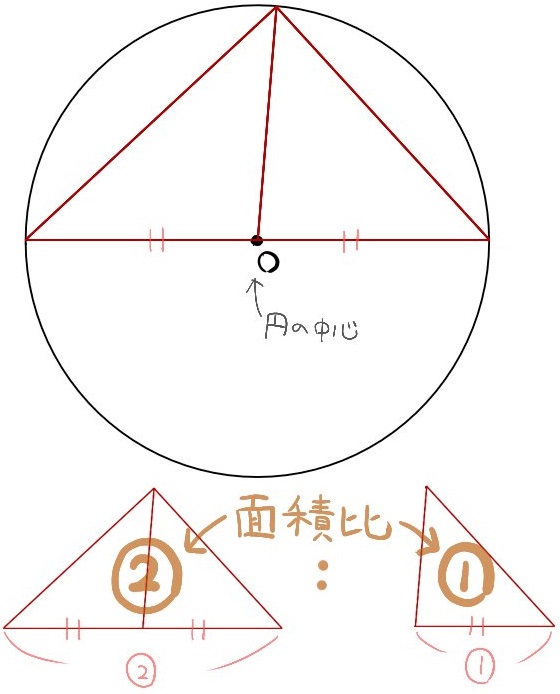直径と半径とそれぞれ底辺としている三角形を比べた場合、２つとも高さが等しいので、その面積比は底辺の長さの比になります。 平行線と三角形の面積比
三角形の面積を二等分する直線の方程式
点Aと線分BCの中点を通る直線の方程式を求めればＯＫです。
線分BCの中点のｘ座標は
点Bのｘ座標と点Cのｘ座標の平均
線分BCの中点のｙ座標は
点Bのｙ座標と点Cのｙ座標の平均
となります。
角の二等分線と面積比
次の図は線分ADが∠BACを二等分しています。
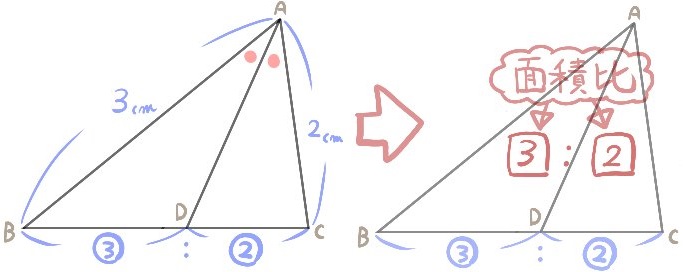
このような場合
線分AB：線分ACの長さの比が３：２なので
線分BDと線分CDの長さの比が３：２となります。（比が同じになる）
したがって
△ABDとACDの面積比は（高さが等しく底辺の長さの比が３：２なので）３：２となります。
問題：上の説明図において、△ABC：△ADCを求めよ。
相似比を使った面積比の求め方
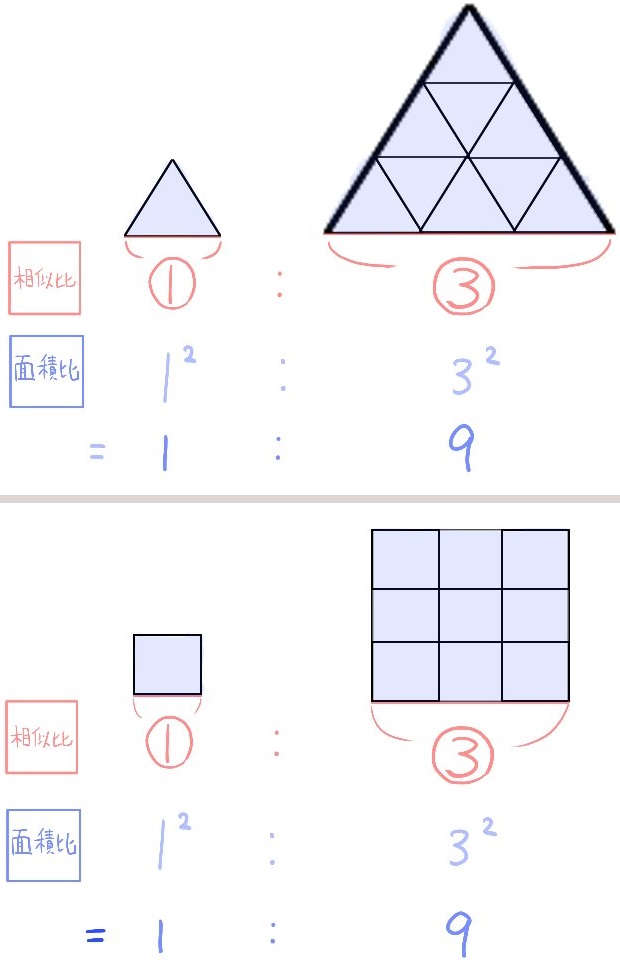
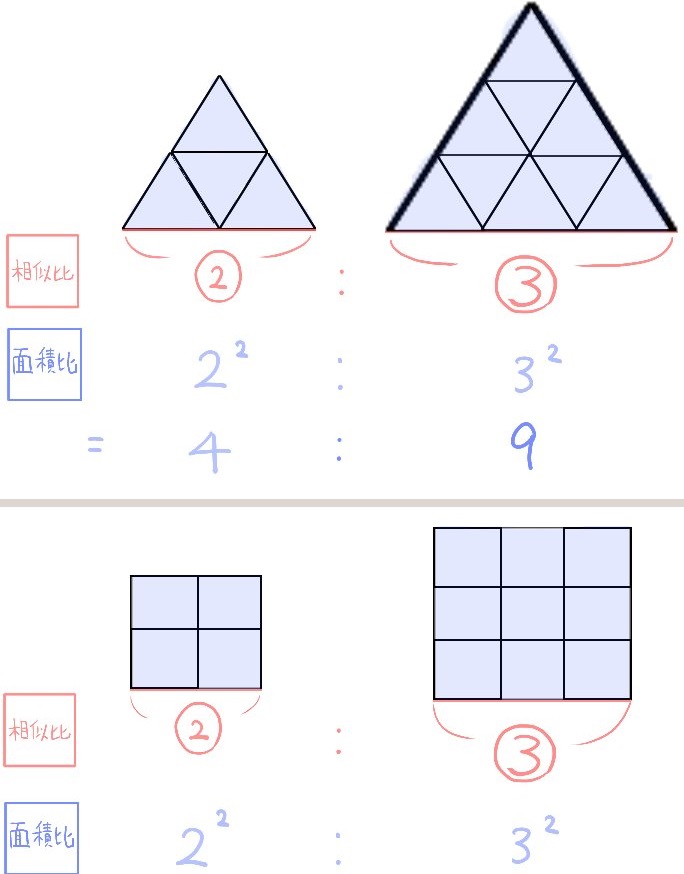これも先程と同様、相似比を２乗すると面積比（タイルの数の比）となっています。
３つの三角形の面積比の問題
３つの三角形A、B、Cがあり、その面積比は
A:B=2:3
B:C=1:2
である。
三角形Aと三角形Cの面積比を求めよ。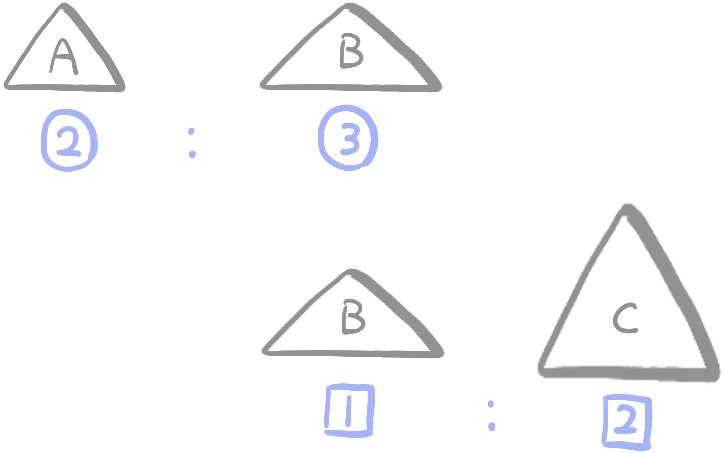
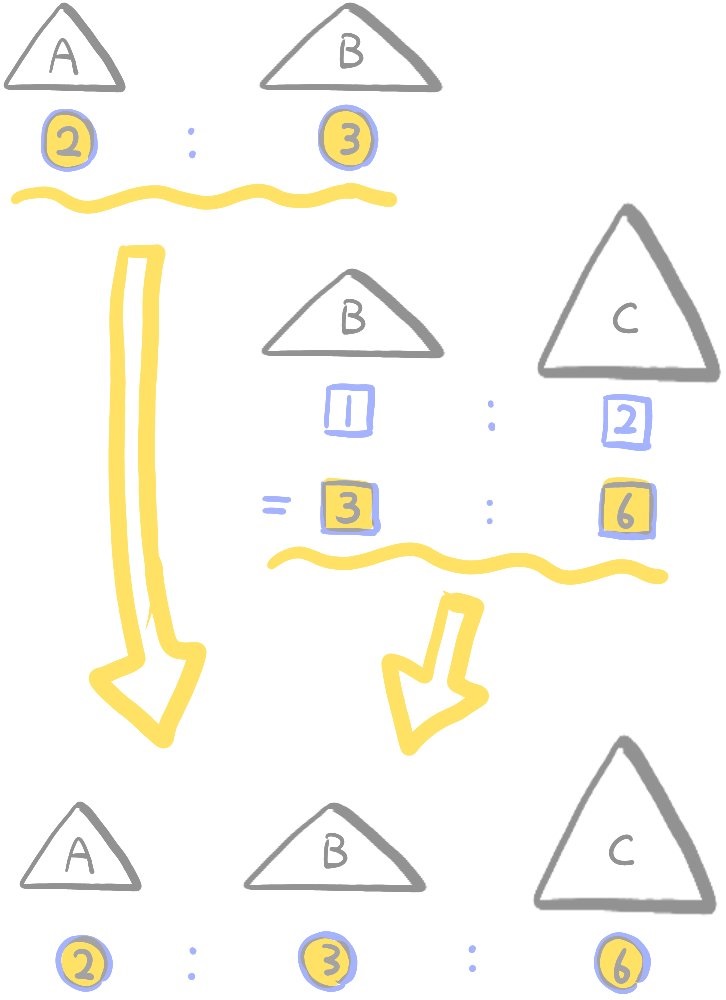A:C=2:6=1:3 ３つの三角形A、B、Cがあり、その面積比は
A:B=2:3
B:C=4:5
である。
三角形Aと三角形Cの面積比を求めよ。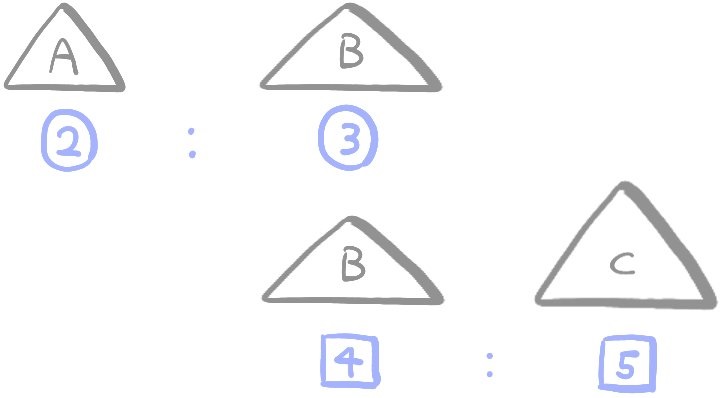
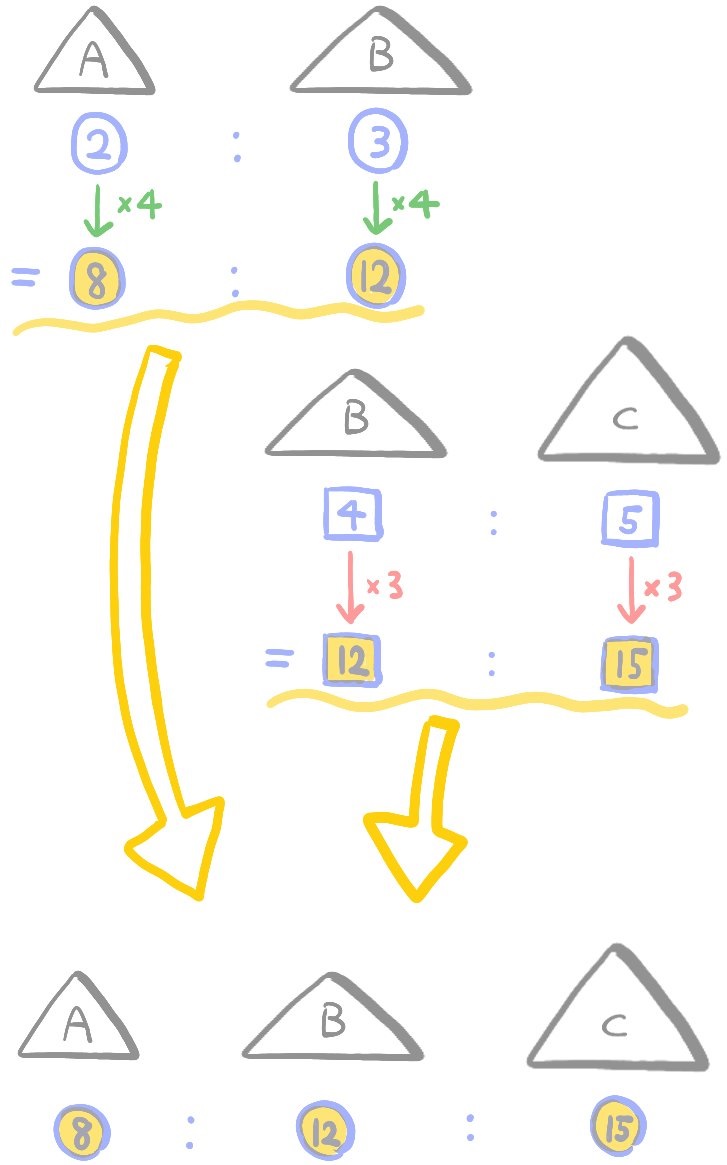
解説にあったように、Bについての面積比を３と４の最小公倍数１２として考えると３つの三角形の面積比を比べることができます。
座標平面上の三角形の面積比を扱うテクニック
次のように平行線を利用し、三角形の面積を同じままに頂点だけを平行移動すると、面積が同じまま、別の三角形を書くことができます。
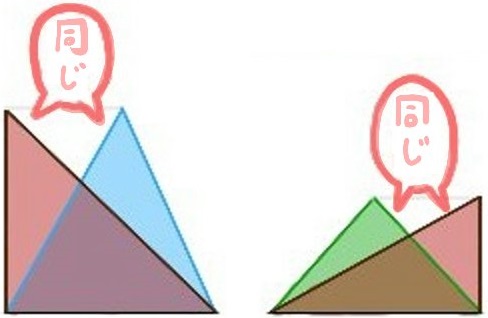
これを利用すると、次のように、四角形を「面積を変えることなく」三角形に変形することができます。
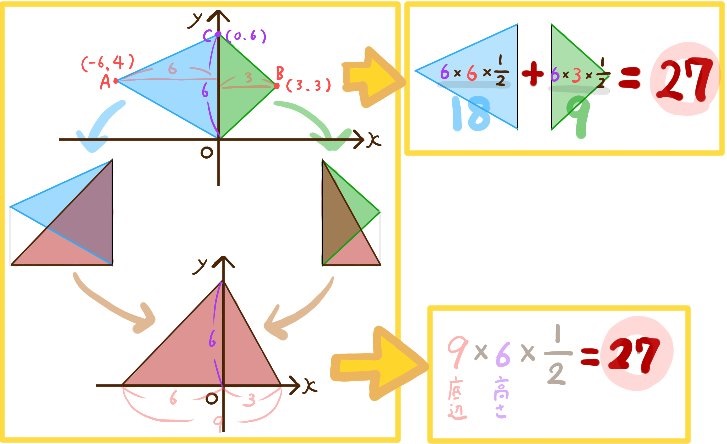
座標平面上に次のような点A、B、C、Dがある。
このとき、△ABOと四角形AOBDの面積比を求めよ。
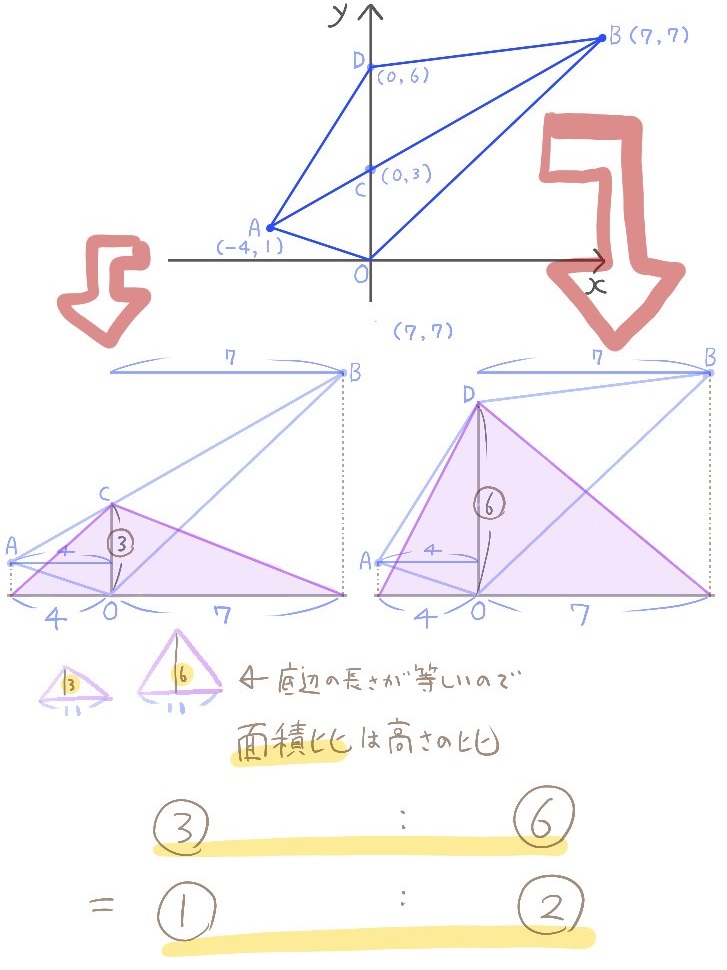
△ABOと同じ面積の△ABDと
△ABOの２倍の面積の△ABEを考える。
点Dと点Eの座標をそれぞれ求めよ。
ただし、点D、点Eはともにy軸上にあり、
点Dのｙ座業は点Cのｙ座業よりも大きく
点Eのｙ座標は点Cのｙ座標よりも小さいものとする。
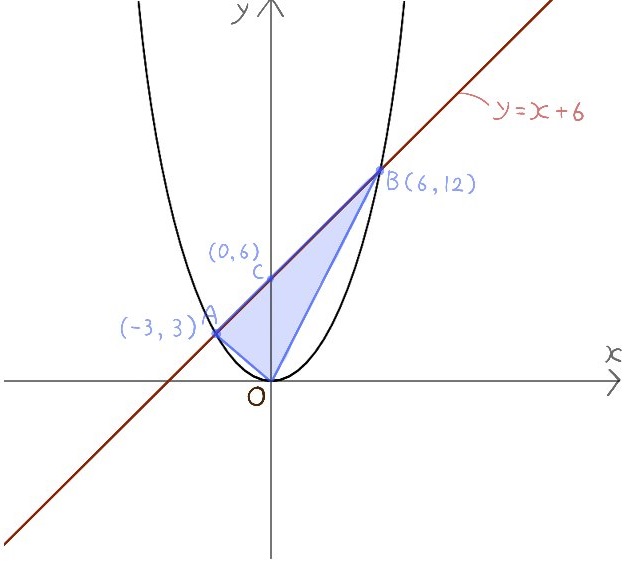
点A,点Bはともに関数 \(y=\dfrac{1}{3}x^{2}\) 上にある。
△ABOと同じ面積の△ABPと
△ABOの２倍の面積の△ABQを考える。
点Pと点Qの座標をそれぞれ求めよ。
ただし、点Pのx座標は、x＞6で、かつ関数 \(y=\dfrac{1}{3}x^{2}\) 上にある。
また、点Qはx座標は、x＞0で、かつx軸上にあるものとする。
平行線を補助線に引くことで、三角形の面積を変えることなく求めたい三角形の形へと変形することができます。これを利用します。
１：平行な直線の方程式は傾きが等しい。
２：放物線と直線の交点の座標は連立方程式の解である。
この二つについても知っておいてください。
学習ページ：平行線の補助線で解く放物線の応用問題
学習ページ：等積変形をグラフで応用し座標平面上の三角形の面積を求める手順
【復習用】平行四辺形における面積比の問題
次の図のような平行四辺形ABCDについて考える。
線分BDはこの平行四辺形の対角線であり∠ABCの角の二等分線である。
また、点Eは線分BCの中点である。
このとき
面積比△ABF：△BEF：△AFD：四角形CDFE
について求めよ。
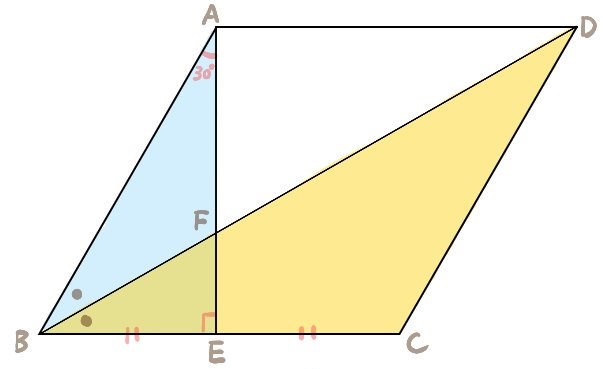
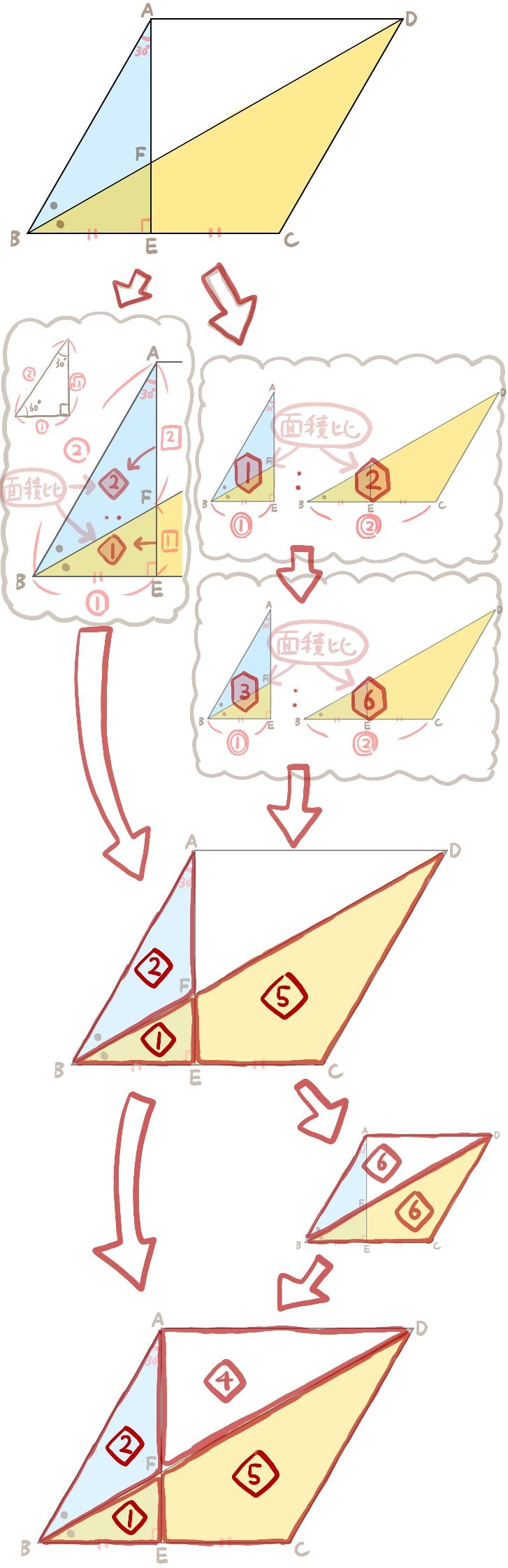
１：三平方の定理
２：角の二等分線
３：高さが等しく底辺の長さが１：２の三角形の面積比
４：平行四辺形の対角線BDは平行四辺形の面積を２等分する
学習ページ：三平方の定理を使う平面図形の難問たち｜中学数学～高校入試
点A(10,6)
点B(-5,3)
点C(4,-11)
がある。
この３点を頂点とする三角形の面積を２等分する直線の方程式を求めよ。