にゃんこ
比例は１次関数なのに、なぜ反比例が１次関数でないのでしょうか。その理由がわかりません。わかりやすく教えてください。
坂田先生
このページでは、なぜ反比例が１次関数でないのか？その理由をていねいに解説します。
にゃんこ
中学数学のまとめプリント(無料)はこちら。
反比例が１次関数でない理由
坂田先生
この説明をする前に、ひとつ確認しておかなければいけないことがあります。
それは、反比例は１次関数ではないが、関数ではあるということです。
坂田先生
めっちゃ大事な確認は以上です。この流れのまま本題の説明に入ります。
そもそも、関数であるとはどういうことでしょうか。
すこし、用語のおさらいをしておきましょう。
ｘの値が決まると、ｙの値がただひとつに決まるとき、『ｙはｘの関数である』と言えます。
坂田先生
ｘに数を代入して計算したら、ｙの値がポンとひとつ出てくるってことです。
これらはすべて関数です
坂田先生
yをxの式で表したときに、\(x\) があったら１次関数、\(x^{2}\) があったら２次関数、と覚えている方は多いかもしれません。
にゃんこ
となると、\(y=\dfrac{2}{x}\)には\(x\) があるから１次関数じゃないの？
坂田先生
そうなりますよね。でも違います。僕も中学生のときに同じ疑問を抱きました。
にゃんこ
\(x^{2}\) が登場するのは２次関数というのは、感覚的にわかりやすいけど、どうして反比例は１次関数ではないのですか？
坂田先生
実はこのことを感覚的に理解するには、指数というものを知る必要があります。
\(x^{2}\) ←指数とは、この右上の２という数のことです。
高校数学では、中学数学で学習している2乗や3乗だけでなく 1乗や0乗、-2乗や-3乗なんかの概念も学習します。
表にするとこうなります。
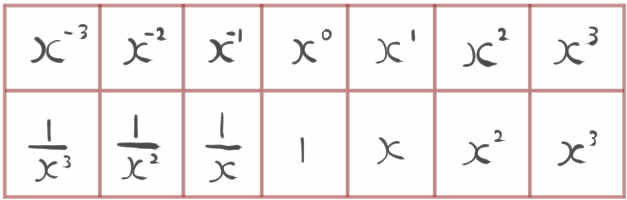
なぜ0乗が1になるのか？という疑問を持った方もいるでしょうが、とりあえず『そうなっとるんだ』と思っておいてください。
とにかくこの話で重要なのは1乗と-1乗のところです。
\(x^{1}=x\)
\(x^{-1}=\dfrac{1}{x}\)
このふたつを知っておく必要があります。
さきほどの式を観察すると、このように分類できます。
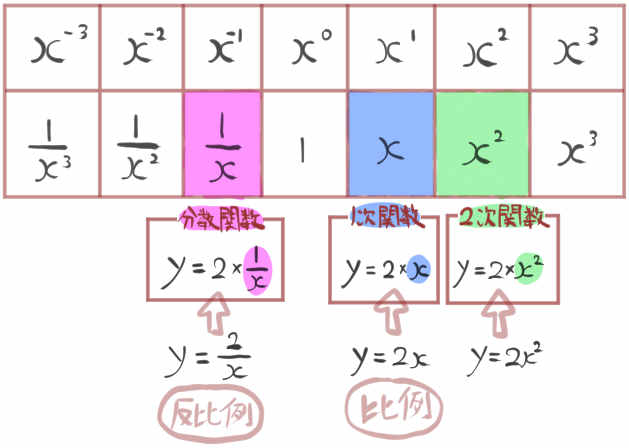
坂田先生
このようにして眺めてみると、反比例のxの式は定数２×\(\dfrac{1}{x}\)という式に変形できて、きれいに \(x^{-1}\)の欄に対応しているような感じがしませんか。
坂田先生
ちなみに反比例の式は『分数関数』という関数に分類されます。
にゃんこ
マイナス１次関数とは呼ばないのですか？
坂田先生
するどい！しかし、マイナス１次関数という呼び名は聞いたことがありませんねえ。高校数学では『分数関数』を学ぶときに登場しますよ。
このテーマの一次関数の話は以上になります。
これらはすべて、ｘの部分に何かしらの数を代入してあげると、その計算結果がｙの値としてひとつ出てきますよね。