


- 公式を使わないで反比例の変化の割合を求める方法
- 反比例の変化の割合の公式を作ってみる
- 反比例の変化の割合の公式を使わないほうがいい理由
公式を使わないで反比例の変化の割合を求める方法

2:xは3から12までは9増えているので、xの増加量(xがどれだけ増えたかという値)は9となる。
3:yの増加量の求め方は、xの増加量の求め方と同じ順番で引き算をする。
つまり、12-3をしたので、それに対応する1-4をする。(4-1ではないということ)
※xが12のときのyの値は1だったので、1を最初にもってくる、ということです。
※ここは、どっちからどっちを引くべきか、意味を考えるとややこしくなるので、xの増加量を求めたときの引き算の順番をマネするだけでOKです。
4:xの増加量が9で、yの増加量が-3だと判明した。
5:変化の割合の求め方は \(\dfrac{yの増加量}{xの増加量}\) なので、 \(\dfrac{9}{-3}=-3\) と判明した。
反比例の変化の割合の公式を作ってみる




xの値が3から12まで増加するとき、変化の割合を求めなさい。
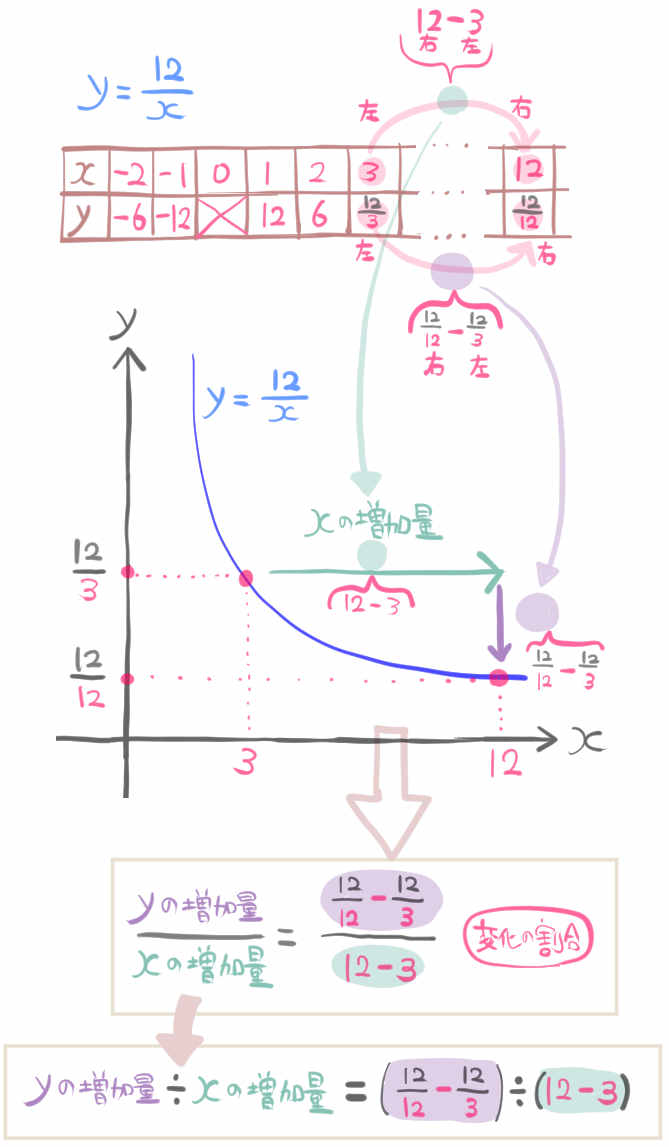
さっきの説明では、9と書いていたところが、ここでは12-3と書いていたりしますね。
つまり、12-3を9と書いてしまわないことで、最初の問題文にあった数「3」と「12」が、どう計算されていったのかがわかるようになっています。
さっきは4と書いていたところが、 ここでは\(\dfrac{12}{3}\) と書いてあったり、1と書いていたところが、 ここでは\(\dfrac{12}{12}\) と書いてあったりしますね。
こうやって書くことで、どうやって変化の割合を求めたのかの計算手順がわかるようになっているのです。
そして一番下にある
xの増加量÷yの増加量= \(\left( \dfrac{12}{12}-\dfrac{12}{3}\right) \div \left( 12-3\right) \)
の部分が公式となる部分です。
もう一度見てください。

赤い数字の3
赤い数字の12
にあたります。
なので、もしも
xの値が△から□まで増加するとき、変化の割合を求めなさい。
という問題があったら、さっきの赤色の3のところに△を代入し、赤色の12のところに□を代入します。
その場合の変化の割合は、このようになります。(途中の計算でややこしい部分がありますが、わからない場合はとばして大丈夫です。)
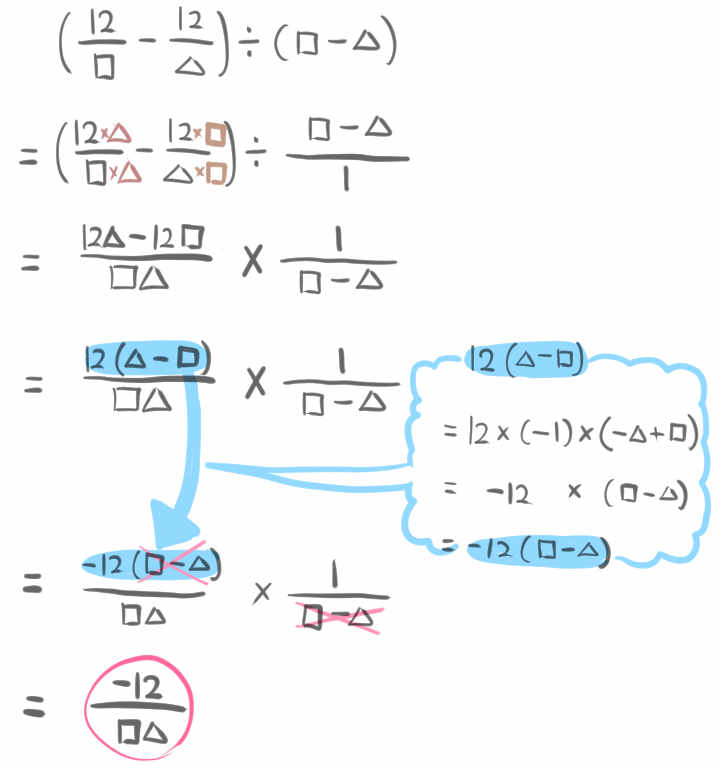

あとは、「\(y=\dfrac{12}{x}\) において」という部分を「\(y=\dfrac{a}{x}\) において」としてやると、さっきの計算はこうなりますね。
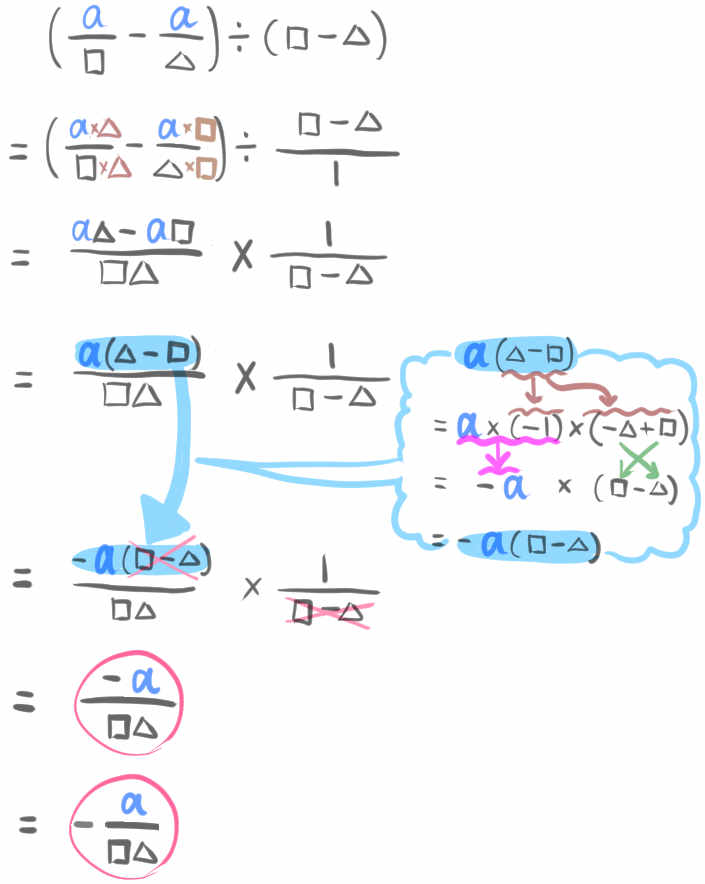
以上の流れを復習するとこうなります。(難しく感じてもざっと眺めるだけでOKです)
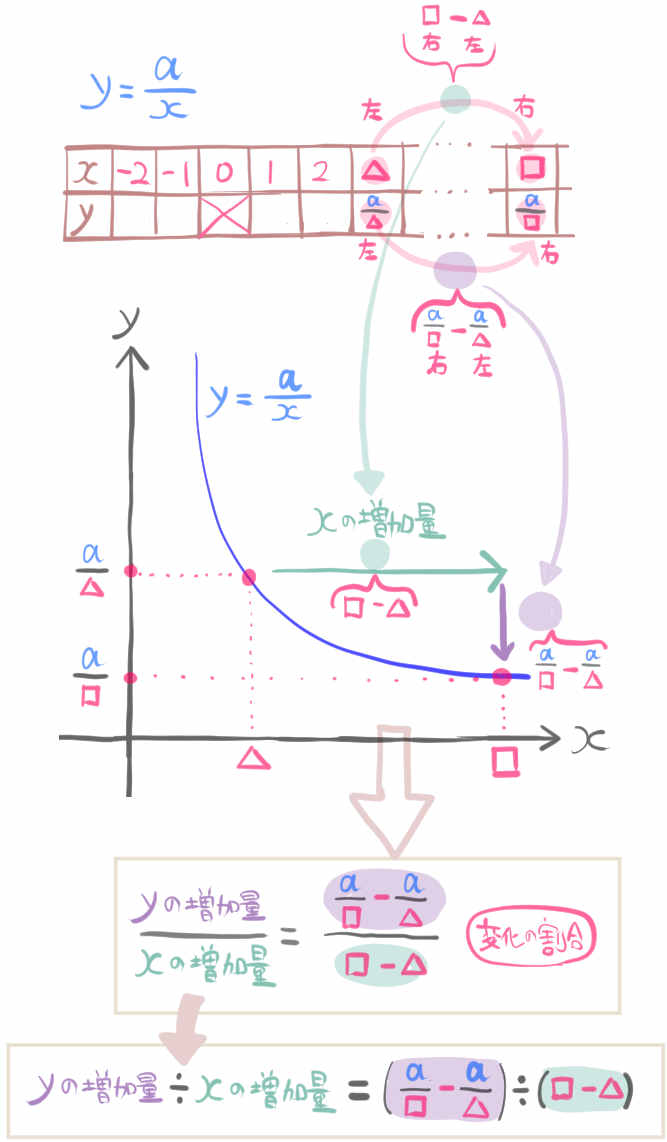


反比例\(y=\dfrac{a}{x}\)における
xの値が△から□まで増加するときの変化の割合の公式は
変化の割合= \(-\dfrac{a}{□△}\) となる。

反比例の変化の割合の公式を使わないほうがいい理由



yの値が12から4まで減少するときの変化の割合を求めよ。
xの値が1から5まで増加するとき、変化の割合は3になる。定数aの値を求めよ。



































xの値が3から12まで増加するとき、変化の割合を求めなさい。