

- 3点から等距離にある点の座標の求め方
- 3点から等距離にある点を求める手順の意味を解説(別解あり)
- 【別解2】3点から等距離にある点を円の方程式で求める
参考:2点から等距離にある直線の式の求め方2通りと公式3つ
参考:3点を頂点とする三角形の面積を求める公式|原点を通る場合通らない場合
参考:線分の垂直二等分線の方程式の求め方2通りと公式
3点から等距離にある点の座標の求め方

3点\(A(10,10),B(-4,8),C(-6,2)\)から等距離にある点Pの座標を求めなさい。





※それぞれやっていることの意味はその後で解説します。








3点から等距離にある点を求める手順の意味を解説










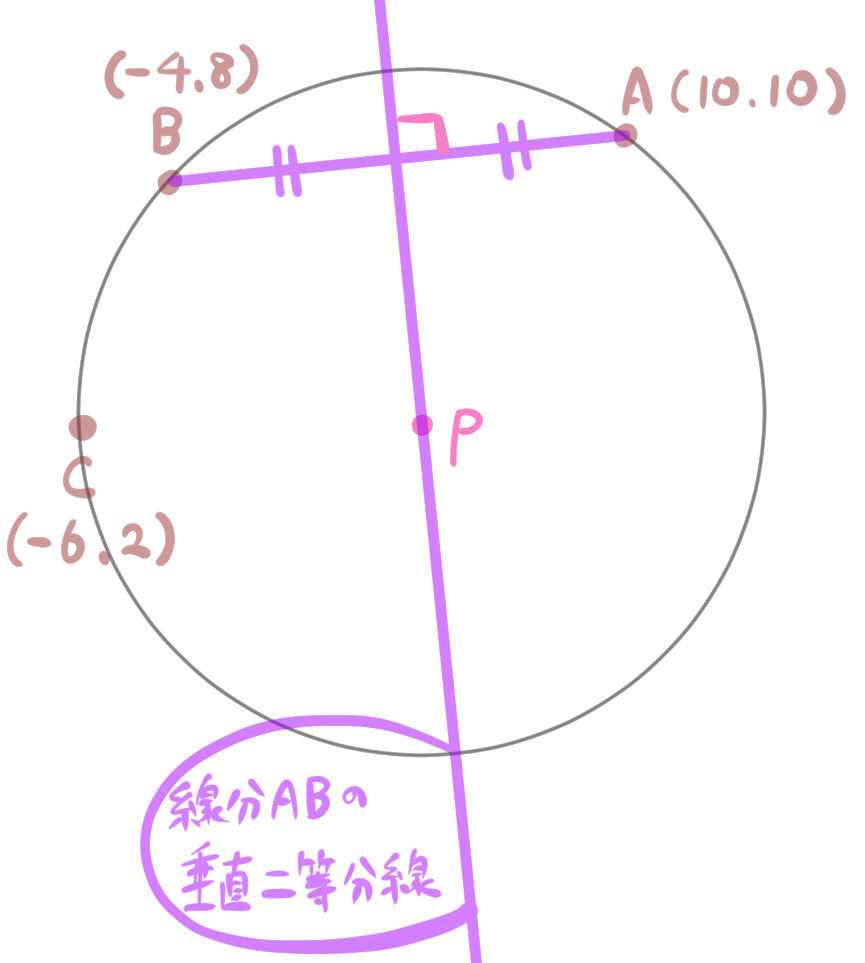


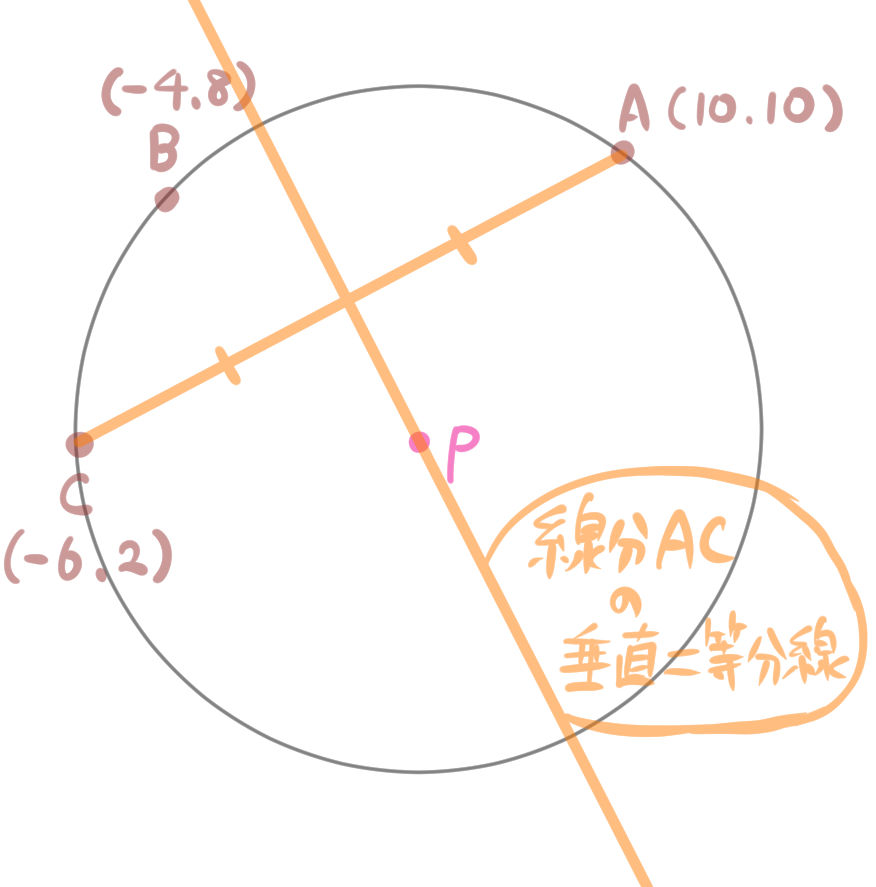








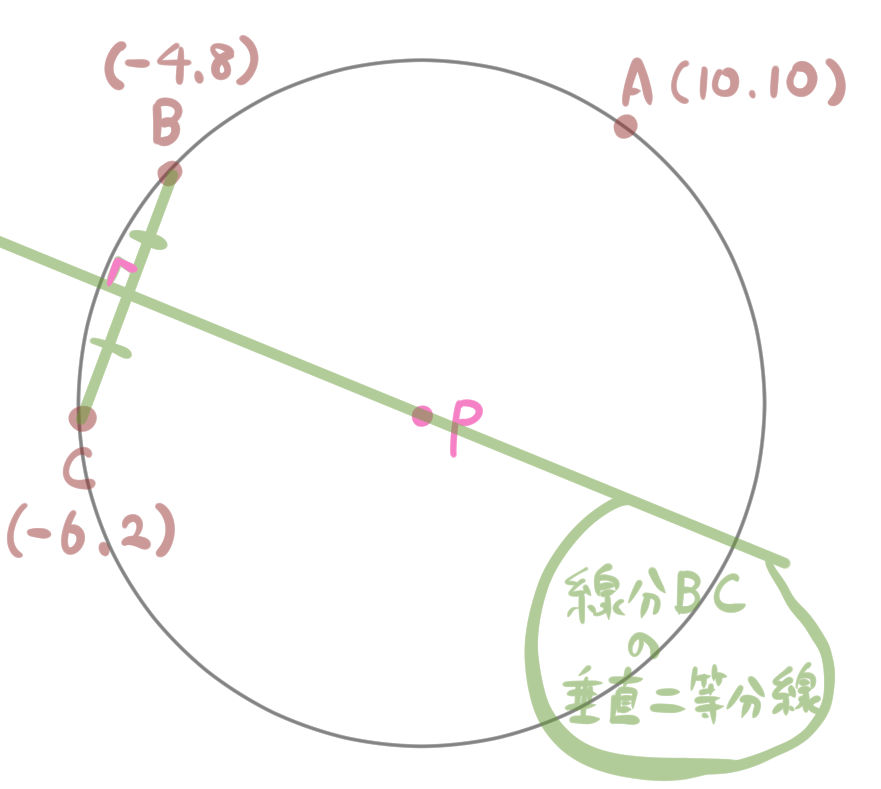






【1】直線ABの傾きを求め、その垂線の傾きaを求める。
【2】2点の中点の座標を求め、そのx座標y座標を代入し、y切片bを求める。
詳しい解説ページ:線分の垂直二等分線の方程式の求め方2通りと公式

【別解2】3点から等距離にある点を円の方程式で求める


手順1:3点を通る円の方程式を求める。
手順2:その円の中心の座標を求める。(これが求める座標P)


3点\(A(10,10),B(-4,8),C(-6,2)\)から等距離にある点Pの座標を求めなさい。
(ただし、円の方程式の一般形を利用しなさい。)
円の方程式の一般形は:\(x^{2}+y^{2}+lx+my+n=0\)
基本形に直すと:\(\left( x+\dfrac{l}{2}\right) ^{2}+\left( y+\dfrac{m}{2}\right) ^{2}=\dfrac{l^{2}+m^{2}-4n}{4}\)
このとき、円の中心の座標は\(\left( -\dfrac{l}{2},-\dfrac{m}{2}\right) \)

求める点Pは、3点A、B、Cを通る円の中心の座標である。
この円の方程式を\(x^{2}+y^{2}+lx+my+n=0\)とする。
この円が
\(A(10,10)\)を通るから
\(10^{2}+10^{2}+10l+10m+n=0\)
\(B(-4,8)\)を通るから
\(\left( -4\right) ^{2}+8^{2}-4l+8m+n=0\)
\(C(-6,2)\)を通るから
\(\left( -6\right) ^{2}+2^{2}-6l+2m+n=0\)
これらを整理して
\(\begin{cases}10^{2}+10^{2}+10l+10m+n=0\\
\left( -4\right) ^{2}+8^{2}-4l+8m+n=0\\
\left( -6\right) ^{2}+2^{2}-6l+2m+n=0\end{cases}\)
これを解くと\(l=-8\)、\(m=-4\)、\(n=-80\)となる
円の中心の座標は\(\left( -\dfrac{l}{2},-\dfrac{m}{2}\right) \)であるから
点Pの座標は\(\left( -\dfrac{-8}{2},-\dfrac{-4}{2}\right) \)
すなわち\((4,2)\)
参考:2点から等距離にある直線の式の求め方2通りと公式3つ
参考:3点を頂点とする三角形の面積を求める公式|原点を通る場合通らない場合
参考:線分の垂直二等分線の方程式の求め方2通りと公式




























