


- 有理数と無理数の違い
- 有限小数、循環小数、循環しない無限小数の違い
- 練習問題1:有理数・無理数編
- 練習問題2:有限小数・循環小数・循環しない無限小数編
有理数と無理数の違い
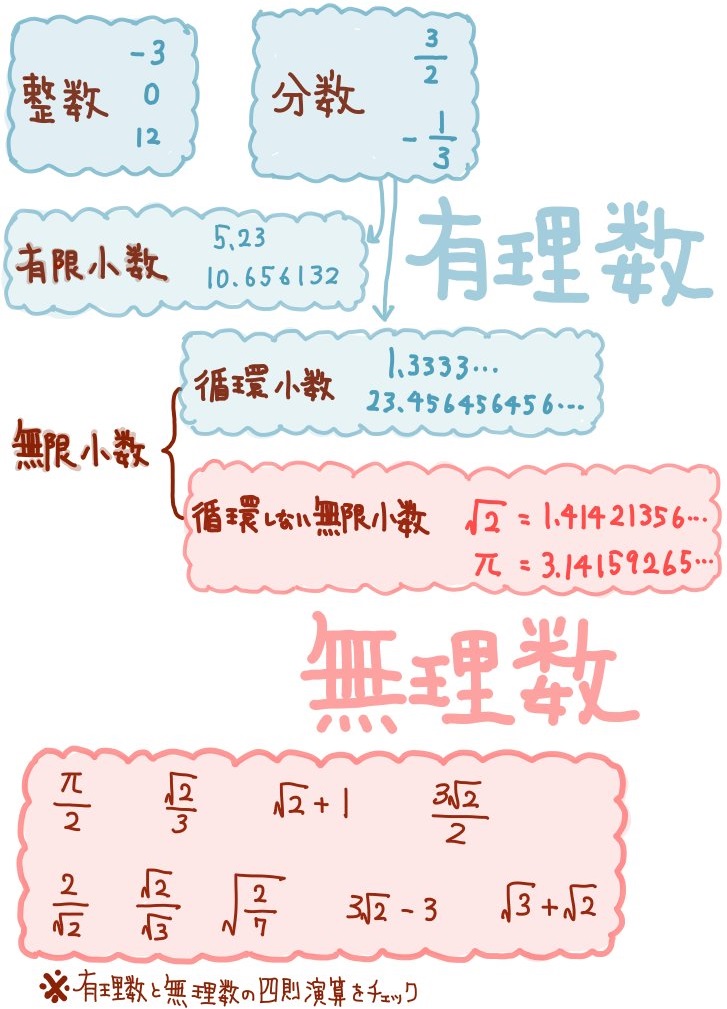
- 整数
-3、0、1、7など
- 分数
\(\dfrac{1}{2}\) 、 \(-\dfrac{101}{3}\) など - 有限小数
1.6
15.83629475617753
など
不規則に続く小数であったとしても、どこまでも続く小数でない(有限小数)なら、分数のかたちに表現することができます。
- 循環する無限小数
1.23456565656…=\(1.234\dot{5}\dot{6}\)
1.23456456456456…=\(1.23\dot{4}5\dot{6}\)
例えば1.6395827413…のように
不規則にどこまでもつづく小数は、分数で表すことができません。
不規則にどこまでもつづく小数のことを循環しない無限小数と言います。

\(\sqrt{2}\) =1.41421356…
π=3.141592653…
このように平方根の記号を消すことができない値や、円周率πが循環しない無限小数にあたります。
有限小数、循環小数、循環しない無限小数の違い


有限小数とは、小数点以下のある桁において、値の表現がとどまる小数のこと。
例:5.3
例:12.3456
これらは分数のかたちに表すことができるので有理数です。
無限小数とは、小数点以下がかぎりなくつづく小数のこと。
無限小数には、規則的な繰り返しがあってつづくもの(循環小数)と、不規則にどこまでもつづくもの(循環しない無限小数)の2種類がある。

例:5.3333333…
例:12.3456565656…
例:12.3456456456…
※これら循環小数は分数のかたちに表すことができるので、有理数になります。

例:3.14159265…
例:1.41421356…
※これらは、分数のかたちに表すことができないので無理数です。(ただし、ここで言う分数のかたちとは、分母が0以外の整数かつ、分子が整数となる分数のことです。)
有理数と無理数の四則演算
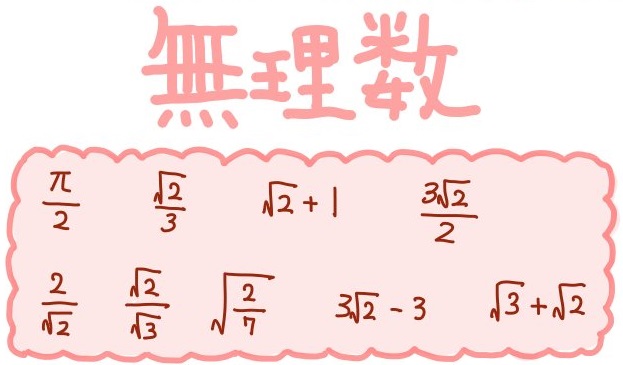
有理数+無理数=無理数
有理数-無理数=無理数
無理数+有理数=無理数
無理数-有理数=無理数
例:\(1+\sqrt{2}\)は無理数
有理数×無理数=無理数(ただし、有理数が0なら結果は有理数0)
無理数×有理数=無理数(ただし、有理数が0なら結果は有理数0)
例:\(2\sqrt{2}\)は無理数
例:\(\dfrac{2}{5}\sqrt{3}\)は無理数
有理数÷無理数=無理数(ただし、有理数が0なら結果は有理数0)
例:\(\dfrac{3}{\sqrt{3}}\) は無理数
無理数÷有理数=無理数
例:\(\dfrac{\pi }{2}\)は無理数
無理数+無理数
無理数-無理数
無理数×無理数
無理数÷無理数

計算結果が無理数になる例
\(\sqrt{2}+\sqrt{3}\) =無理数
\(\sqrt{2}+\sqrt{2}\) =無理数
計算結果が有理数になる例
\(\sqrt{2}+\left( -\sqrt{2}\right)\) =0(有理数)

練習問題1:有理数・無理数編

- 13
- \(\sqrt{2}\)
- \(-\sqrt{16}\)
- \(6\sqrt{2}\)
- π
- \(\dfrac{\pi }{2}\)
- 13.43892734
- \(1.234\dot{5}\dot{6}\)
- \(1.23\dot{4}5\dot{6}\)
- 自然数
- 0
- 負の整数
- \(\dfrac{3\sqrt{2}}{5}\)
- \(2\sqrt{2}-2\)
- 循環しない無限小数
- 有限小数
- 循環小数
\(-\sqrt{16}=-4\)なので有理数です。
\(6\sqrt{2}\)は、有理数6×無理数\(\sqrt{2}\)なので、無理数となります。
※有理数×無理数=無理数(ただし、有理数が0の場合は結果は有理数0)
円周率πは
π=3.141592653…
と循環しない無限小数なので、分数のかたちに表現できません。
よって、円周率πは無理数となります。
円周率πは
π=3.141592653…(無理数)
なので、 \(\dfrac{\pi }{2}\)は無理数となります。

13.43892734は、不規則ではあるが有限小数なので、分数のかたちになおすことができます。よって有理数です。
これがどこまでも不規則に続く『循環しない無限小数』であれば分数のかたちになおすことができず、無理数となっていました。
整数はすべて有理数です。よって、自然数も有理数です。
0も整数なので有理数です。
\(\dfrac{0}{5}\) のように、分数のかたちに表現できます。
負の整数も整数なので、有理数です。
\(\dfrac{3\sqrt{2}}{5}=\dfrac{3}{5}\times \sqrt{2}\)
つまり、有理数 \(\dfrac{3}{5}\) ×無理数 \(\sqrt{2}\) なので無理数です。
※有理数×無理数=無理数(ただし、有理数が0の場合は結果は有理数0)
\(2\sqrt{2}\) は有理数2×無理数\(\sqrt{2}\) なので無理数です。
※有理数×無理数=無理数(ただし、有理数が0の場合は結果は有理数0)
\(2\sqrt{2}-2\)は、無理数\(2\sqrt{2}\) -有理数2なので、無理数です。
※無理数-有理数=無理数
練習問題2:有限小数・循環小数・循環しない無限小数編

- \(\dfrac{7}{5}\)
- \(\dfrac{7}{3}\)
- \(\dfrac{7}{11}\)
- \(\sqrt{10}\)
- \(2\sqrt{2}-2\)
\(\dfrac{7}{5}=\dfrac{14}{10}=1.4\) となり、有限小数となります。
\(\dfrac{7}{3}=7÷3=2.33333…\) となり、循環小数となります。
\(\dfrac{7}{11}=7÷11=0.6363636…\) となり、循環小数となります。
\(\sqrt{10}\) は無理数です。無理数は小数で表すと、循環しない無限小数になります。
\(2\sqrt{2}-2\)は無理数です。(解説は、上の14番の問題をご覧ください)
無理数は小数で表すと循環しない無限小数になります。
































mを整数、nを0でない整数とする。
有理数とは、 \(\dfrac{m}{n}\) のように分数で表すことができる数である。
無理数とは、\(\dfrac{m}{n}\) のように分数で表すことができない数である。