


平方根や有理数・無理数の正誤問題

- \(\sqrt{5}\)を2倍したものは\(\sqrt{10}\)である。
- 25の平方根は5である。
- \(\sqrt{25}=\pm 5\)
- 5の平方根は\(\sqrt{5}\) である。
- \(\sqrt{25}\) の平方根は \(\pm \sqrt{5}\)である。
- \(\sqrt{\left( -3\right) ^{2}}=-3\)
- 2乗すると10になる数は\(\sqrt{10}\) であり、2乗すると100になる数は10である。
- \(\sqrt{\dfrac{1}{4}}\)は無理数である。
- 0は有理数である。
- \(\left( \sqrt{2}+\sqrt{3}\right) \left( \sqrt{2}-\sqrt{3}\right) =-1\)
- \(\sqrt{10}-\sqrt{3}= \sqrt{10-3}\)
- \(x^{2}=1\) ならば \(x=1\) である。
- \(\sqrt{0.01}=0.1\)
- 正の数aの平方根とは、2乗してaになる数であるから、つまり \(\sqrt{a}\) である。
- x+y、xyがともに有理数であるならば、2つの数x、yはともに有理数である。
- 有理数と無理数の和は必ず無理数になる。
- 有理数と無理数の差は必ず無理数になる。
- 有理数と無理数の商は必ず無理数になる。
- 有理数と無理数の積は必ず無理数になる。
\(\sqrt{5}\)を2倍したものは\(2\sqrt{5}\)です。
正しくは
25の平方根は \(\pm 5\) である。
です。


正しくは \(\sqrt{25}=5\) です。


\(-\sqrt{25}\)は2乗して25になる値のうち-の値、という意味です。
なので次の3つはすべて正しいです。
\(\sqrt{25}=5\)
\(-\sqrt{25}=-5\)
\(\pm\sqrt{25}=\pm5\)
正しくは
5の平方根は \(\pm \sqrt{5}\) である。
です。
\(\sqrt{25}\) =5なので、\(\sqrt{25}\) の平方根とは、5の平方根、つまり\(\pm \sqrt{5}\) のことを指します。
\(\sqrt{\left( -3\right) ^{2}}=\sqrt{9}=3\) が正しい変形です。
正しくは
2乗すると10になる数は±\(\sqrt{10}\) であり、2乗すると100になる数は±10である。
です。
\(\sqrt{\dfrac{1}{4}}=\dfrac{\sqrt{1}}{\sqrt{4}}=\dfrac{1}{2}\) となり、有理数となります。
\(\left( \sqrt{2}+\sqrt{3}\right) \left( \sqrt{2}-\sqrt{3}\right) \\
=\left( \sqrt{2}\right) ^{2}-\left( \sqrt{3}\right) ^{2}\\
=2-3\\
=-1\)
\(5\sqrt{3}-\sqrt{3}=4\sqrt{3}\) のように、ルートの中の数値が等しい場合のみ、足したり引いたりできます。
例えば \(5a-a=4a\) のように、平方根の記号付きの値を文字式の文字のようにとりあつかっていると考えるとわかりやすいです。
正しくは
\(x^{2}=1\) ならば \(x=\pm 1\) である。
です。
xは2乗して1になる値ならば(つまり、xは+1と-1ならば)
xは必ずしも1ではなく、+1か-1なので、命題に当てはまらないケースが出てきます。
そのような場合は『正しくない』と判断します。
\(\sqrt{0.01}=\pm 0.1\) ではありません。
0.01の平方根は \(\pm 0.1\) ですが、それはなぜかと言うと「2乗して0.01になるのは \(\pm 0.1\) です」と言っていることと同じことだからです。
それに対して、 \(\sqrt{0.01}\) は、『2乗して0.01になる値のうち+の値』という意味なので、\(\sqrt{0.01}=0.1\)は正しいということになります。
なので、\(-\sqrt{0.01}=-0.1\) も正しくて、理由は『2乗して0.01になる値のうち-の値は-0.1です』と読み取れるからです。
次の3つの等式は正しいです。
\(\sqrt{0.01}=0.1\)
\(-\sqrt{0.01}=-0.1\)
\(\pm \sqrt{0.01}=\pm 0.1\)
正の数aの平方根とは、2乗してaになる数である
↑この部分は正しいです。しかし
2乗してaになる数は\(\sqrt{a}\) ではなく、±\(\sqrt{a}\)になります。
反例として、
x=\(\sqrt{3}\)
y=−\(\sqrt{3}\)
の場合を考えると
x+yは0で有理数
xyが3で有理数
つまり、x+y、xyがともに有理数であるが
x=\(\sqrt{3}\)
y=−\(\sqrt{3}\)
はともに無理数となります。
反例として
有理数0と無理数\(\sqrt{3}\) の商(0÷\(\sqrt{3}\))は有理数0になります。
反例として
有理数0と無理数\(\sqrt{3}\) の積(0×\(\sqrt{3}\))は有理数0になります。







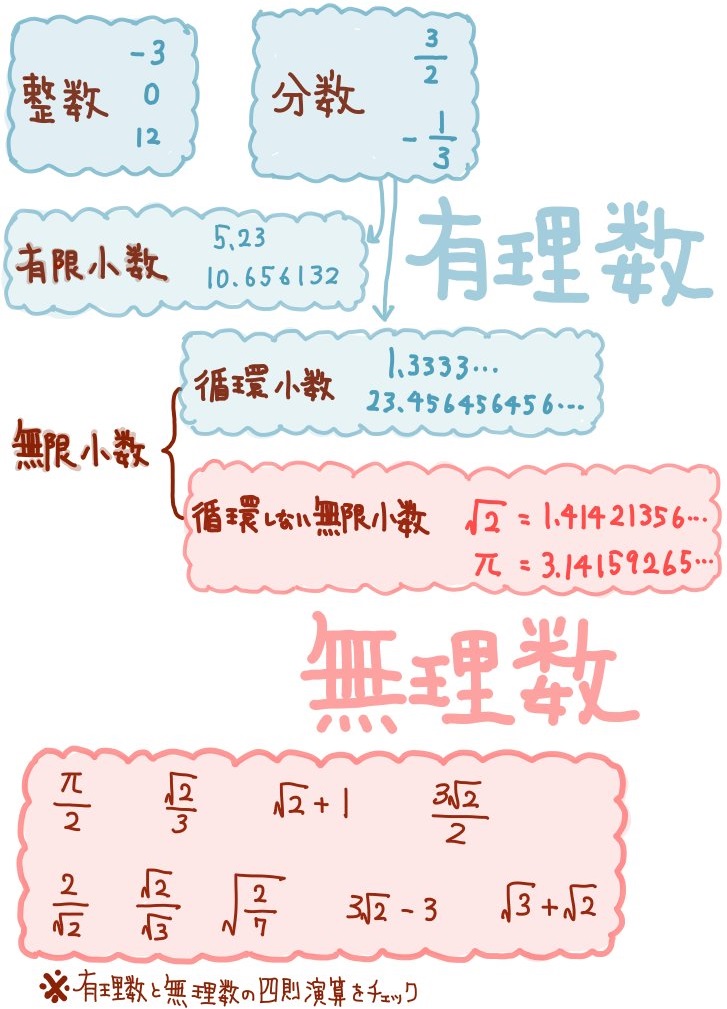





















有理数と無理数の特徴や四則演算など、理解を深めたい方はこちらで学習できるのでご覧ください。
参考:有理数と無理数の違いと四則演算について
