右辺が\(12\times 15\) という掛け算の形で出題されています。

ここでは、この面白い2次方程式の問題の解き方を解説していきます。
右辺が積の形になった2次方程式の面白い問題|普通に解く場合
この2次方程式の問題を、まず普通に解こうとしてみます。
これを、右辺が0になるようにすべて左辺に移項し、同類項を整理してみます。
すると、このようになります。
この次に考えるのが、かけて-182になり、たして1になる2数の組み合わせは何か?ということです。

解いていてる途中で、解が無理数になりそうだと判断した場合は、解の公式や平方完成を使うほうがいいでしょう。
参考:2次方程式の解の公式と平方完成の解き方手順
2数をかけて負の数になるということは、2数は異符号ということになります。
その異符号をたして1になるということは、2数の絶対値の差は1だということですね。
(例えば11と-10の絶対値の差は1になります)
この方針の場合、以下3通りの方法によってその2数を突き止めることができます。
方法2:解の公式や平方完成を使う
方法3:平方数であたりをつける(上級テクニック)
方法1:182を素因数分解して考える
これはこちらで特集した『係数や定数項の大きい場合の因数分解』で練習できるテーマです。
xの係数や定数項が大きい場合は、定数項の部分を素因数分解してから、2数を探すのが効果的です。
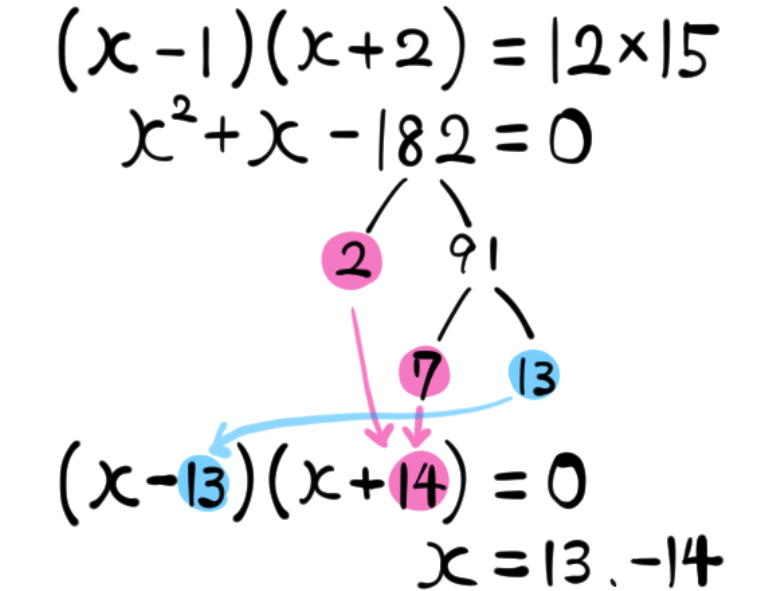
方法2:解の公式や平方完成を使う
この手順の解説は省略します。
方法3:平方数であたりをつける
2数は、絶対値の差が1になり、その積が−182になるというところまでわかりました。
積が負の数になるということから、この2数は異符号だということですが、その絶対値だけを見ると、当たり前ですが、ともに正の数になりますね。(絶対値なので)
この2つの正の数をかけると、当然+182になります。
まずは、この2つの正の数を探すことを考えます。
さらにこの2つの正の数は、ともに182の約数になっています。
探している2つの正の数は、182の約数でかつ、その2数の差が1となる
ということです。
このように、2数の差が近い位置にある場合に有効なのが、『平方数であたりをつける』という方法です。
この問題だと、このようになります。
この不等式からわかることをざっくり説明しますとこういうことです。
\(13\times 13=169\)
\(〇\times △=182\)
\(14\times 14=196\)
差が1となるほど値が近い2つの約数の積で182を作る場合
〇と△は13や14あたりだろうな、という目星がたつ。
‥ということです。
ただし、気を付けてほしいのは、求める2つの正の数が整数として存在するかどうかは不明、だということです。
たまたまこの問題は、13×14=182となり、
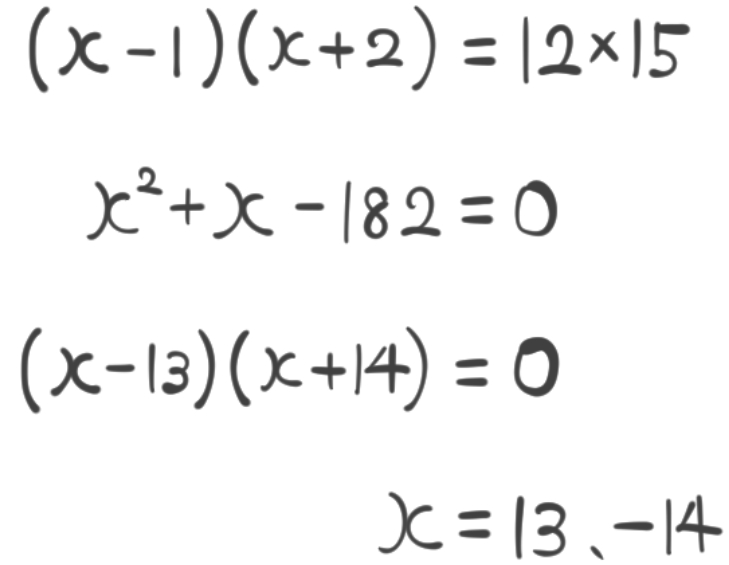
このように解を求めることができましたが、問題によっては2の方法で解決するしかない場合もあります。

2次方程式の面白い問題(制作者の想定した理想的な解き方)

手間さえかければちゃんと解答を得られるのですが、以下の発想に気が付くと、かなりの短時間で解答可能となります。
まず、右辺の正の形がひょっとしたらヒントかも、と疑ってみます。
とりあえず左辺に合うように変形してみたら何か気が付くかも‥と思えたら最高です。
左辺のかたちに合うように、12×15を変形できないかと試みます。
するとこのようになります。
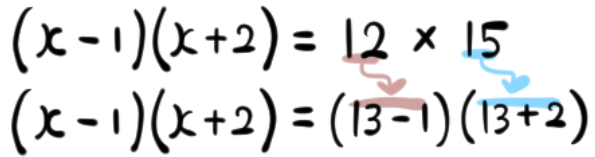
眺めてみて、なにか気が付くことはないでしょうか。
正解はこうです。
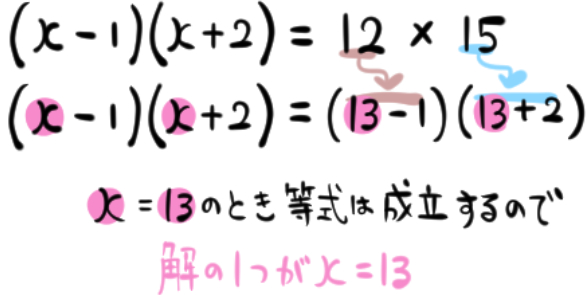
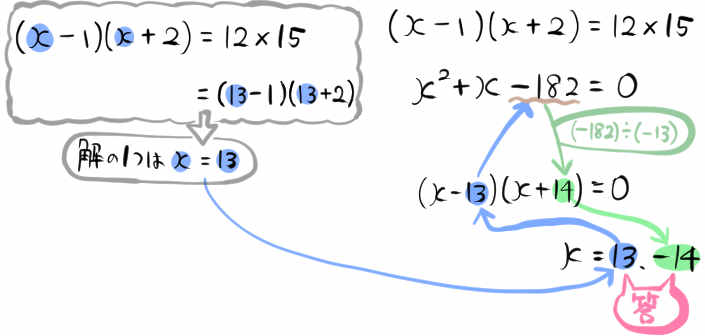
xに13を代入すると、等式が成立するので、二次方程式の解の一つは13だということがわかります。
それを利用して、もう一つの解を求めます。
もとの2次方程式を変形するとこうなります。
この解の一つが13なのですから、この左辺を因数分解した形はここまでわかります。
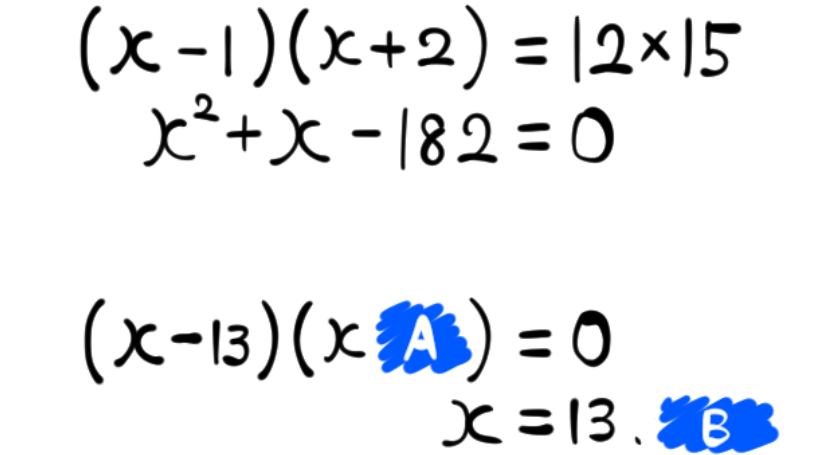
これを見ながらまず【青色のA】を埋めることを考えます。
その結果、もう一つの解も求めることができます。
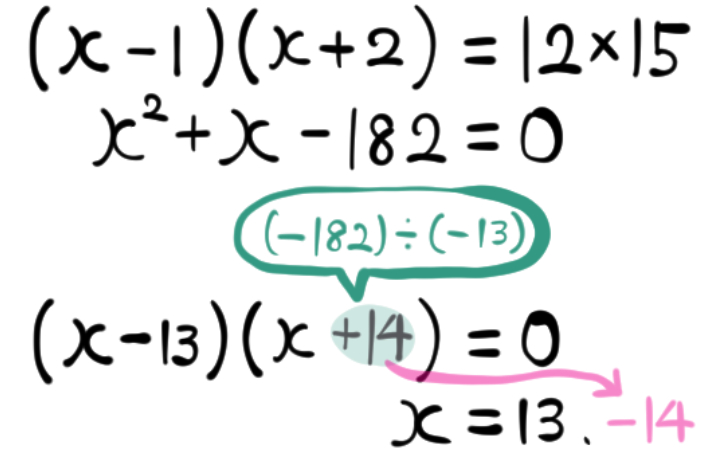
答え: \(x=13,-14\)