中学数学の規則性の問題｜基本～標準
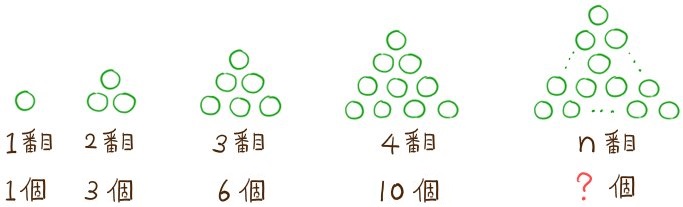
1番目から順に、丸が次のように規則的に並んでいる。このときｎ番目の丸の個数をｎの式で表せ。
学習ポイント
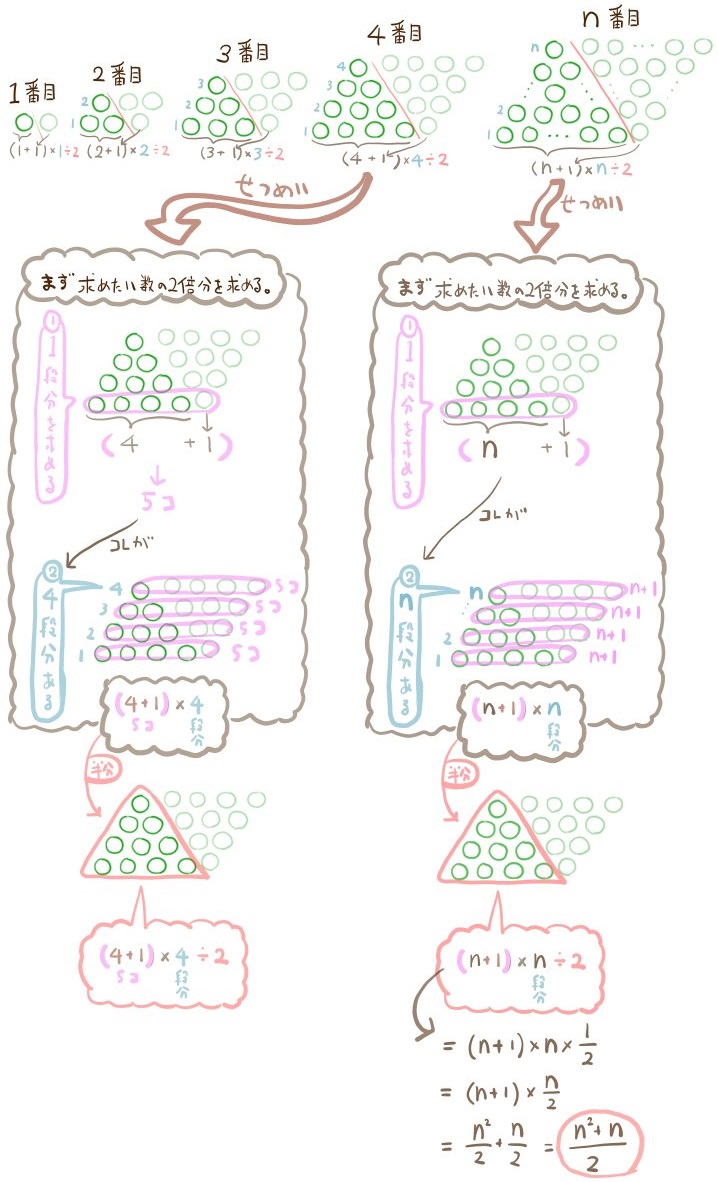
規則性の問題を解くときのコツは、１番目や２番目で式を考えようとしないことです。
最初の番号ほど、規則性を発見しにくいので、この問題のように４番目あたりで規則性や法則性を見つけると解きやすいことが多いです。
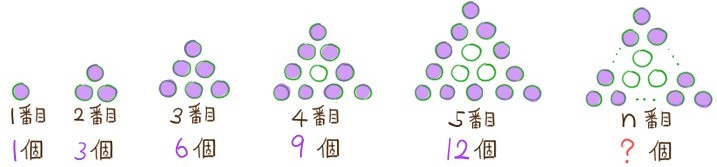
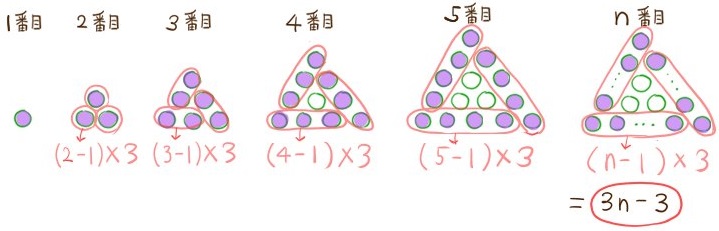
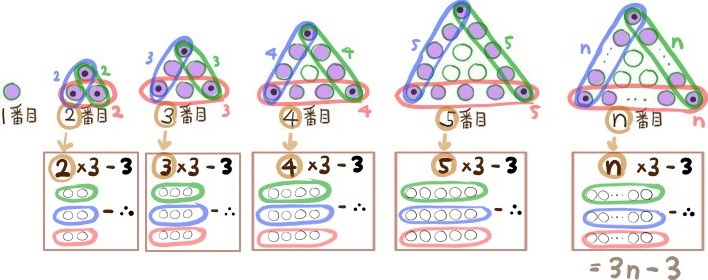
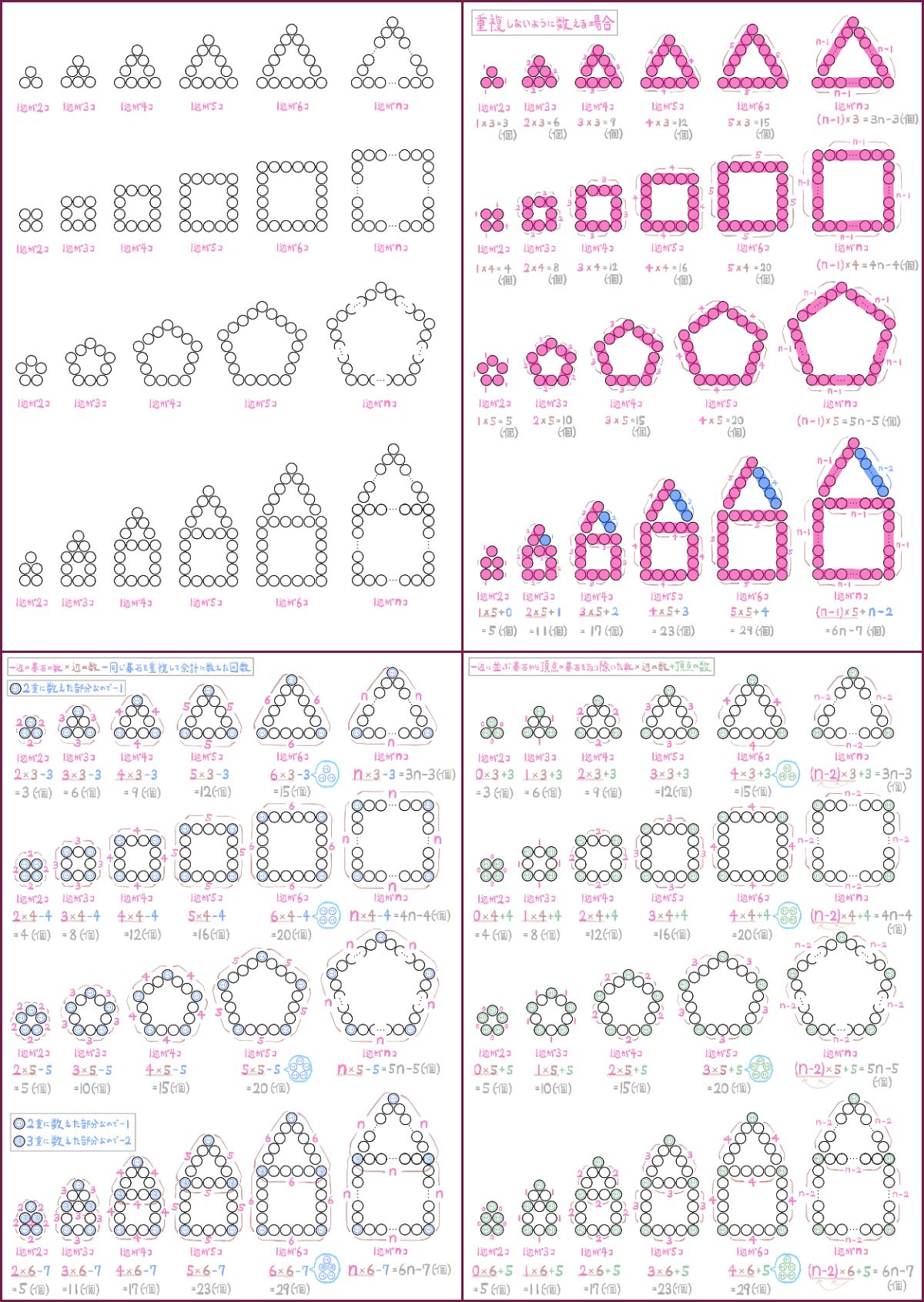
先程の図に対して、次のように最も周りの丸の数について考える。このとき、ｎ番目の数をｎの式を表せ。ただしｎは２以上の自然数とする。
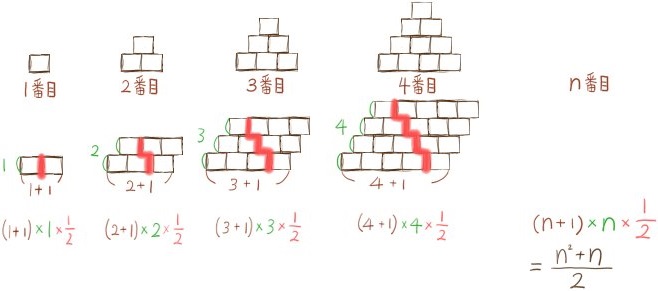
正方形の紙の四隅に画びょうを刺し、壁に貼り付けていく。貼り付ける紙を２枚、３枚と増やすにつれ、次のように規則正しく貼り付けていく。紙をｎ枚使用するときに使う画びょうの数をｎの式で表せ。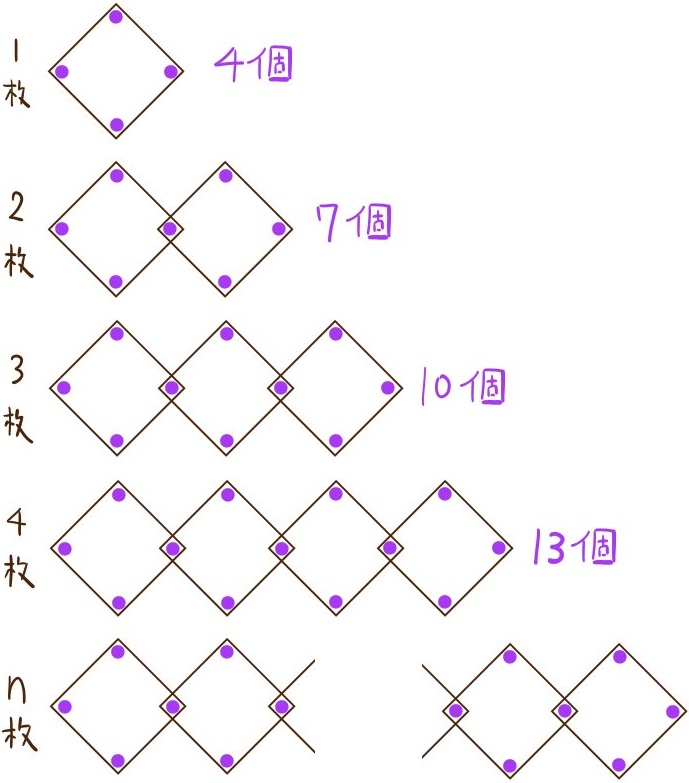
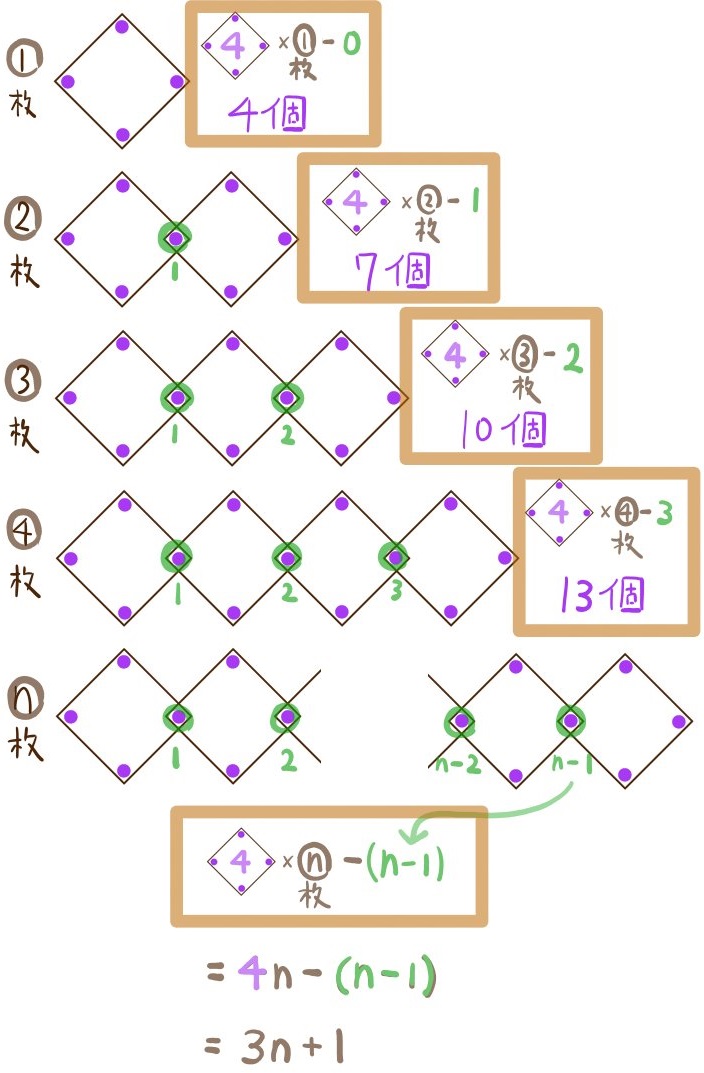
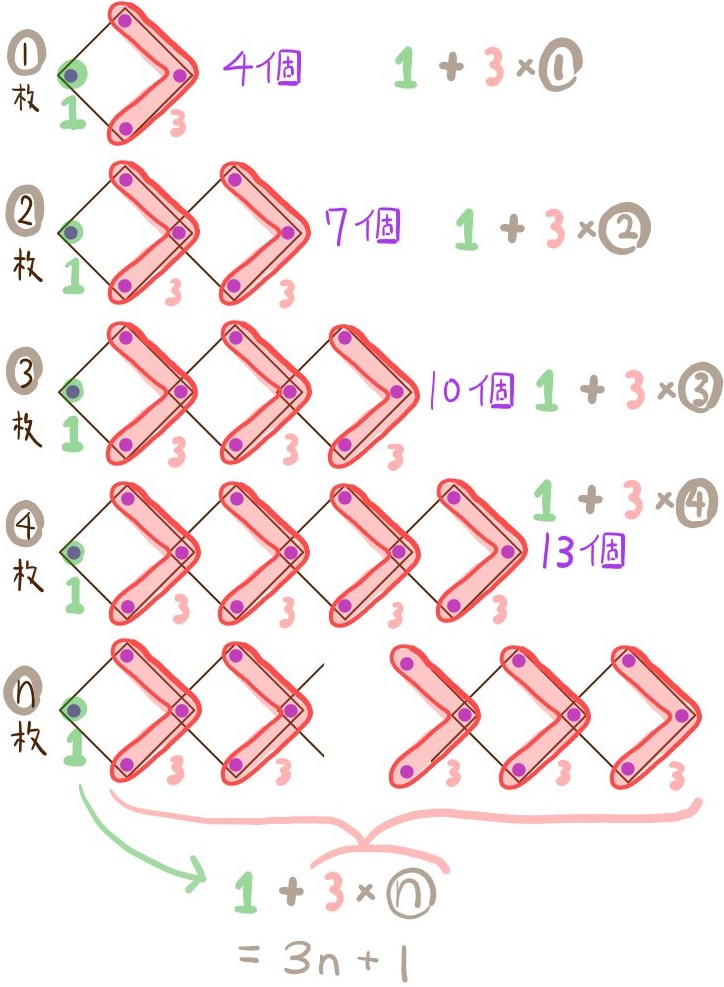
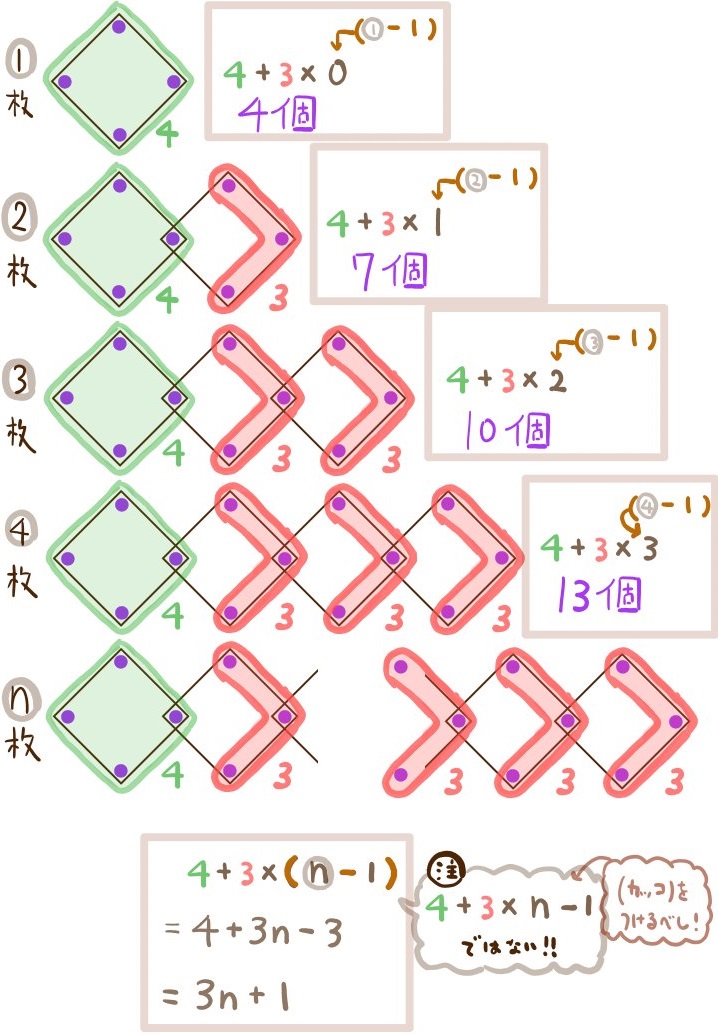
様々な考え方で式を作ることができますが、ここに示したように３通りの考え方でスラスラ式を組み立てられる練習をしておくと理解が深まり、実力が上がります。
縦5㎝、横3㎝の長方形の紙を、のりしろ1㎝で次のように張り合わせていく。
ｎ枚の紙をつなげたときの面積をｎの式で表せ。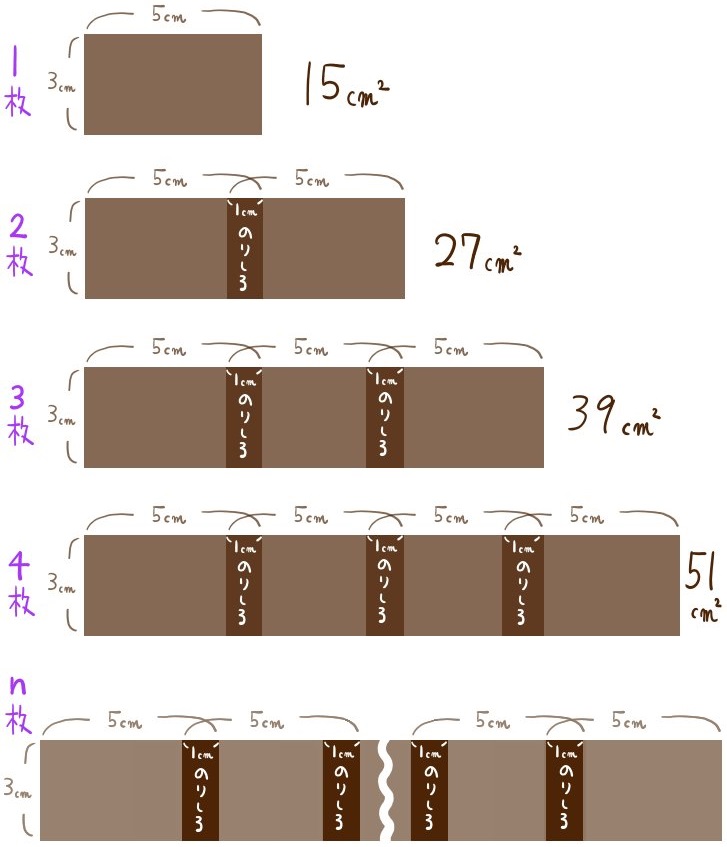
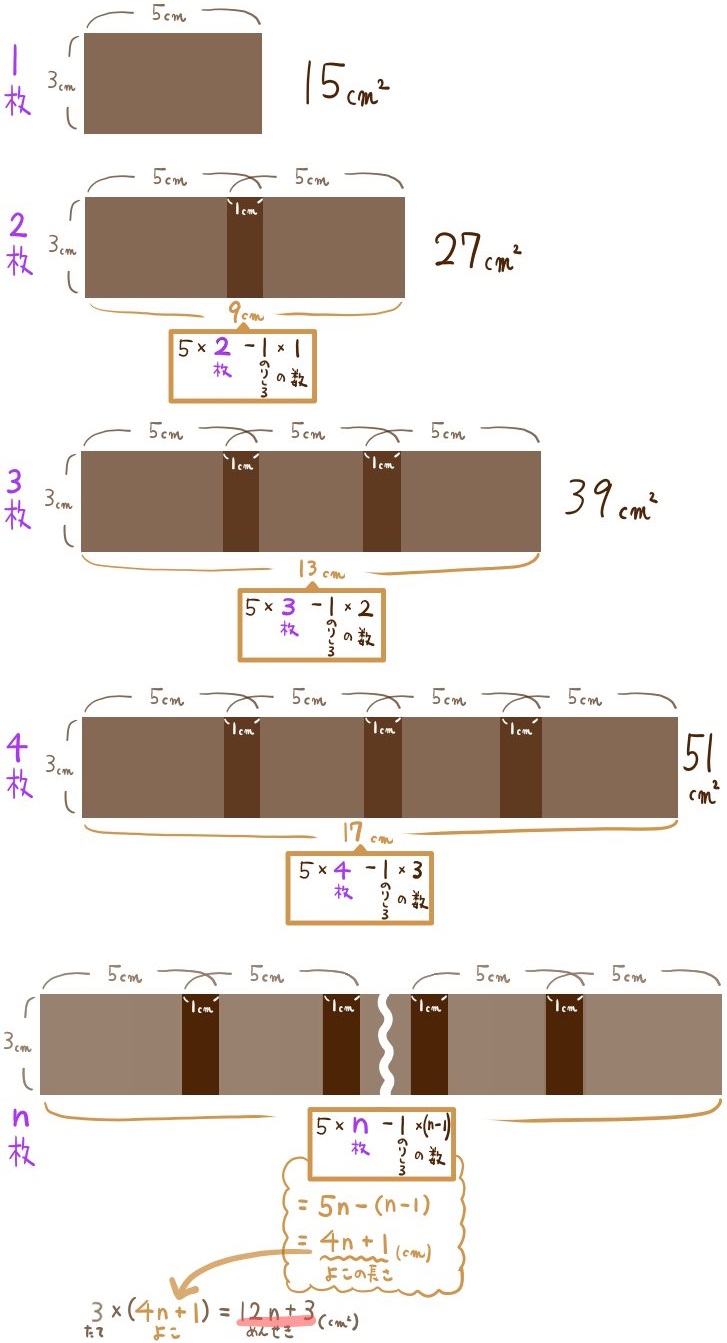
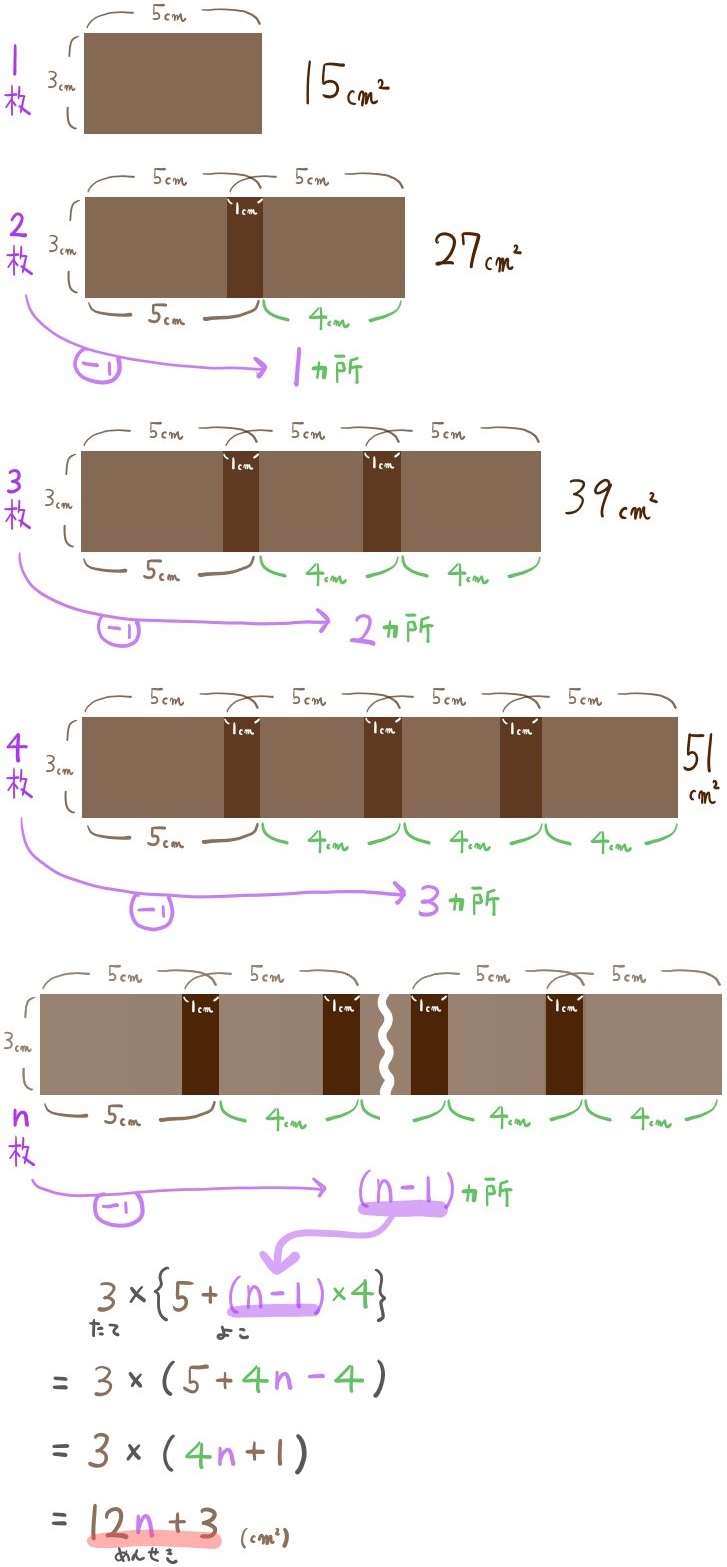
のりしろの長さが2㎝の場合を考えてみると、どちらの考え方のほうが式が作りやすいでしょうか？試してみましょう。
次の図のように、各辺の長さが2㎝の正三角形を、となり合う正三角形どうしの底辺が1㎝ずつ重なるように貼り合わせて図形をつくっていく。実線部分は図形の周を表し、『・』は図形の頂点を表している。
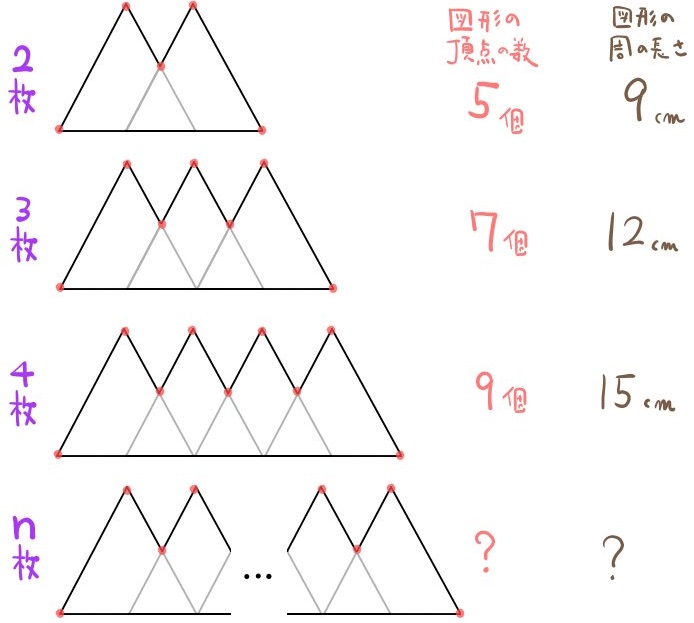
三角形をｎ枚張り合わせたときにできる図形の頂点の数と、周の長さについて、それぞれｎを用いた式で表せ。ただしｎは２以上の自然数とする。
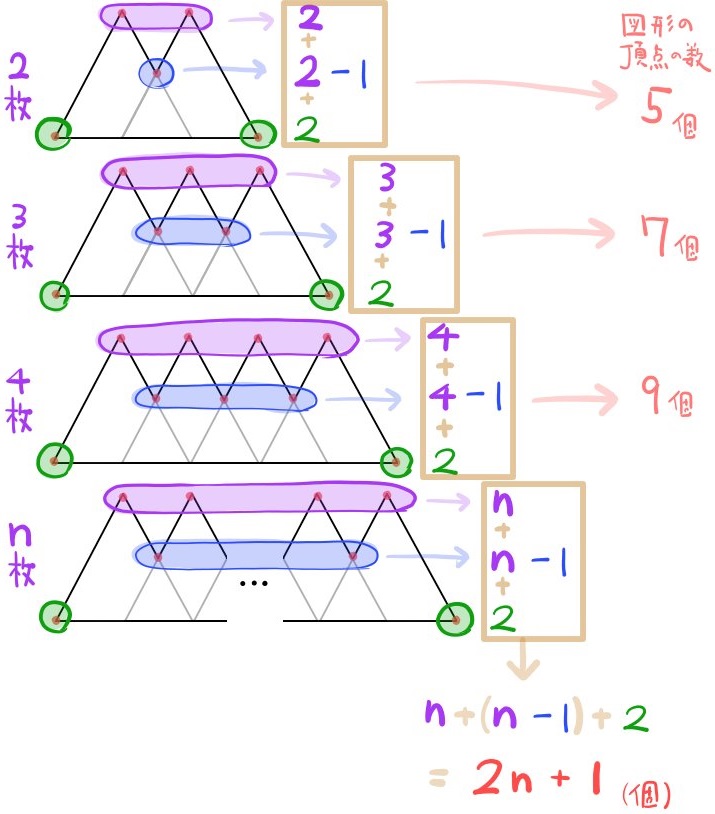
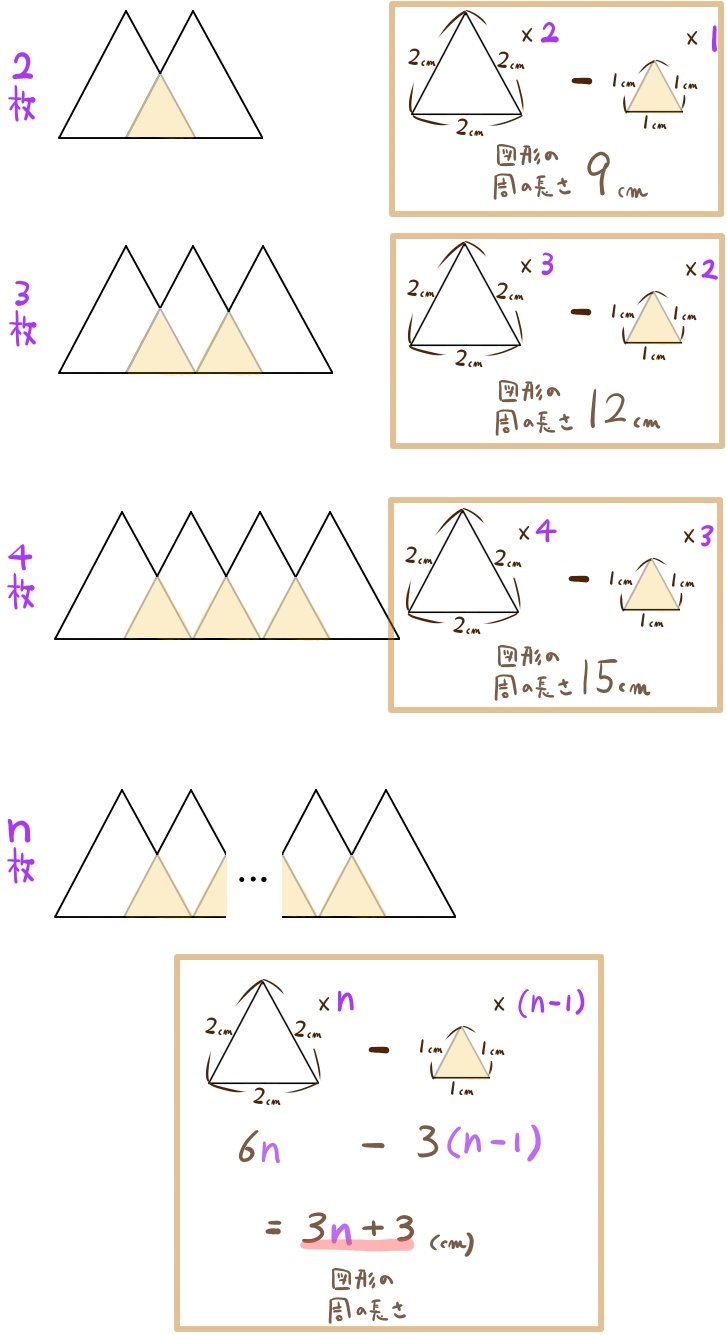
規則性の問題の応用～難問
次のように、数が規則的に並んでいる。次の問いに答えよ。(石川県改)
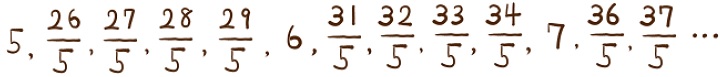
(1) 5と6の間には4つの分数が並んでおり、その和は22である。同様に考えて、7と8の間に並ぶ数の和を求めよ。
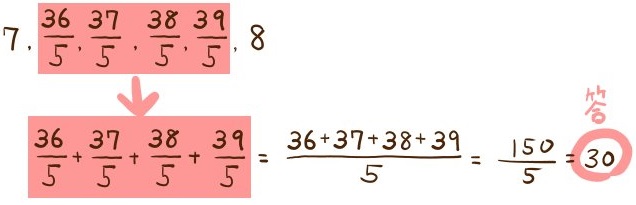
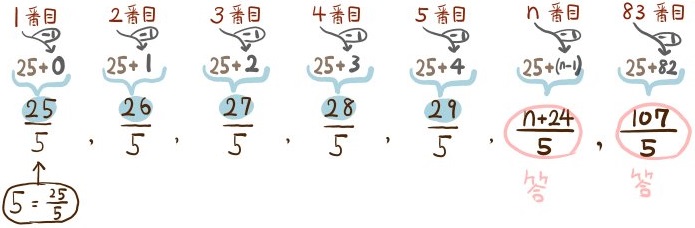
まず、5と6の間に並んでいる数は4個あるという情報から、「では5と7の間に並んでいる数はいくつあるか？」と数えてみます。すると4個に5個を加えた9個である、ということがわかります。次に、「5と8の間に並んでいる数」を数えてみると、さらに＋5個の14個である、ということがわかります。
つまり、最初の4個から、何回5を加えていくか、という見方で式をつくることができそうだ、と気がつきます。
5と6の間に並んでいる数の場合は、4に5を加える回数は0回
5と7の間に並んでいる数の場合は、4に5を加える回数は1回
5と8の間に並んでいる数の場合は、4に5を加える回数は2回
5とxの間に並んでいる数の場合は、4に5を加える回数は(x-6)回
と、なります。
1辺の長さが1㎝の正三角形を三角形Ａとする。
１番目は三角形Ａを１枚使い、２番目は三角形Ａを４枚使い、‥といったように、以下のように、三角形Ａをすきまなく並べ、順番に図形を作ってゆく。
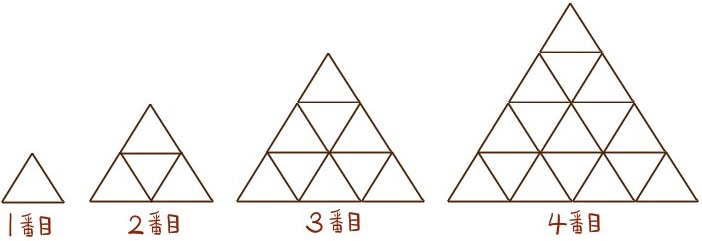
(1) n番目の図形はいくつの三角形Ａでできているか。また、その図形の周りの長さについて、それぞれｎを使った式を表せ。
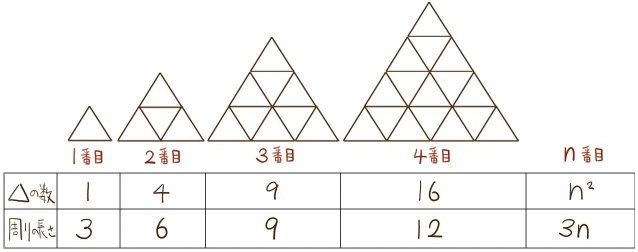
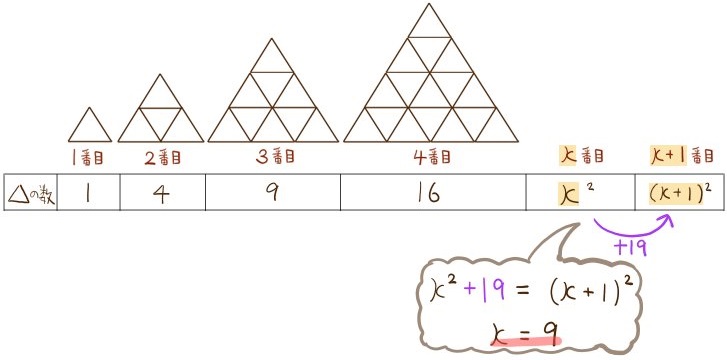
(2)の問題のような解き方も身に付けておきましょう。※このパターンの練習ができる問題が意外と少ないです。
各辺の長さが1㎝の立方体を、次のように、１番目、２番目と順に積んでゆく。また、それらの図形の正面から見た図についても次の通りである。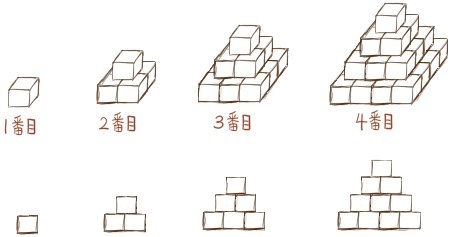
(1) 4番目の図形に使用した立方体の数を求めよ。
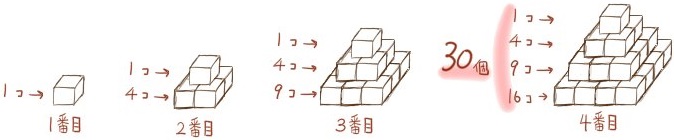
(2) n番目の図形について、正面から見た形の面積をnの式で表せ。
(3) n番目の図形の表面積をnの式で表せ。
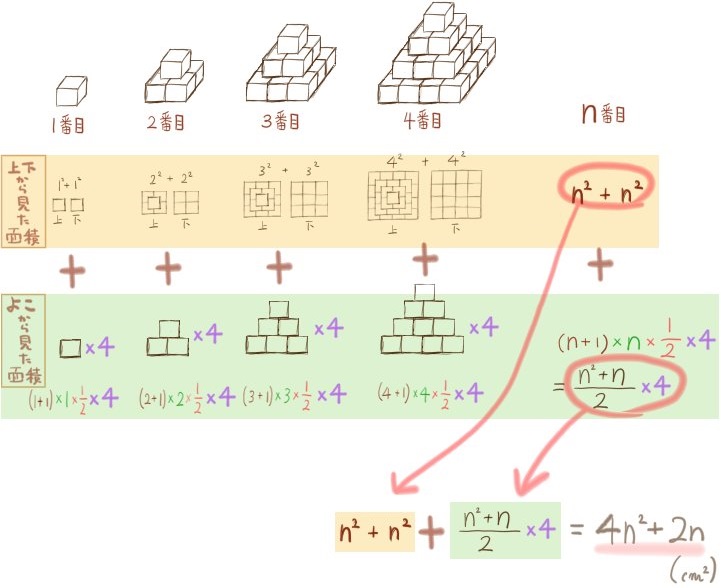
表面積を求める際に、側面から見た面積の合計は、(2)で求めた問題を利用することになります。それに、上から見た図と下から見た図のかたちの面積を合計すると、求める表面積になります。ここの考え方を知っておいてください。
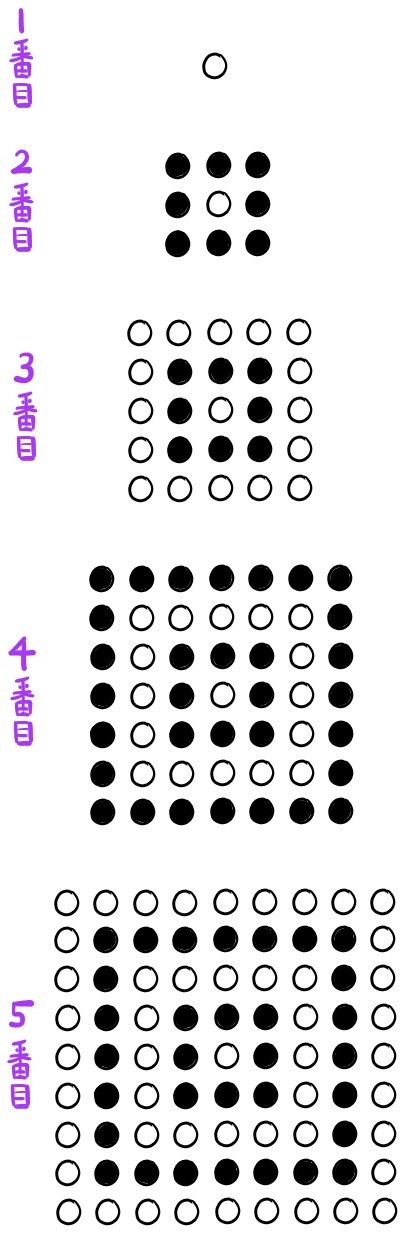
次の操作に従い、白い石と黒い石を順に置いていく。
１番目の操作：白い石を１個置く。
２番目の操作：１番目に置いた白い石の外側に、黒い石を正方形の形に追加して置く。
３番目の操作：２番目に置いた黒い石の外側に、白い石を正方形の形に追加して置く。
ｎ番目の操作：ｎ-１番目に置いた石の外側に、その石と異なる色の意志を正方形の形に追加して置く。ただしｎは２以上の自然数とする。(佐賀：改)
(1)ｎ番目の操作では、ｎ-１番目に置いた石の外側に石を72個追加して置いた。ｎの値を求めよ。
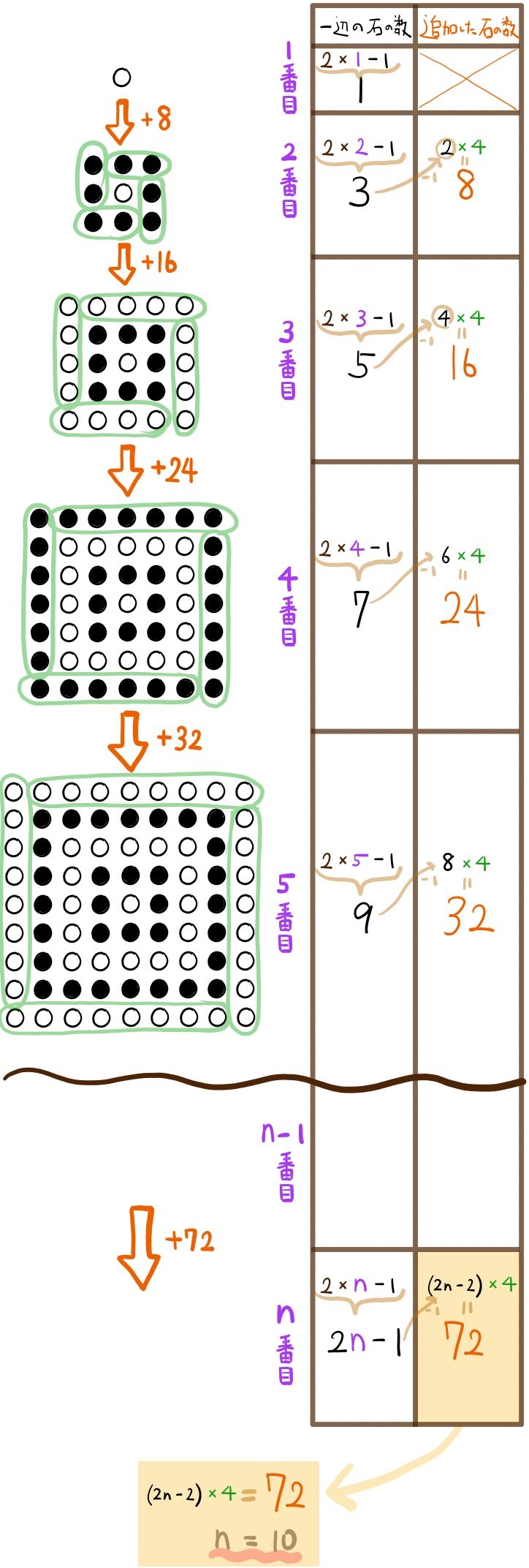
(2)また、(1)のとき白い石は全部で何個あるか求めよ。
ｎの値は10なので、1番目の白の数１個と、10番目までに追加された白い石の数の合計が、求める数になります。
白の石が追加されるのは、奇数番目の操作なので、10番目の操作までにそれは、３番目の操作、５番目の操作、７番目の操作、９番目の操作、と４回あります。
また、ｎ番目の操作により追加される石の数は、 \(\left( 2n-2\right) \times 4=8n-8\)(個)となります。(先程の問題の解説のところにあります。)
よって、３番目の操作、５番目の操作、７番目の操作、９番目の操作で追加された白い石の数は、8n-8のｎに３、５、７、９を代入して求めることができます。
１回目の操作により追加された白い石の数と、その後の４回の操作により追加された白い石の数をそれぞれ求め、その和を計算すると、次のようになります。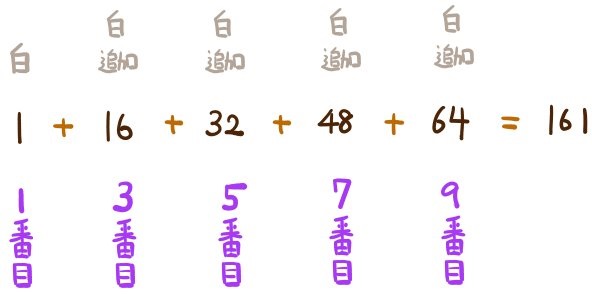
(3)また、(1)のとき黒い石は全部で何個あるか求めよ。
先程の問題と同様に考えます。
黒の石が追加されるのは、偶数番目の操作なので、10番目の操作までに追加された黒い石の数を求めるとこのようになります。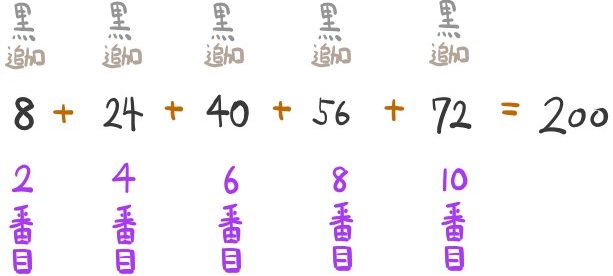
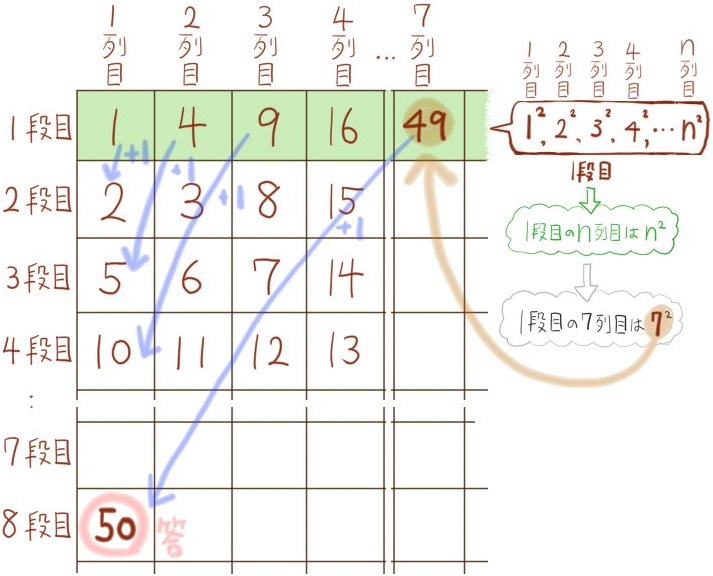
次のように、数を規則的に並べてゆく。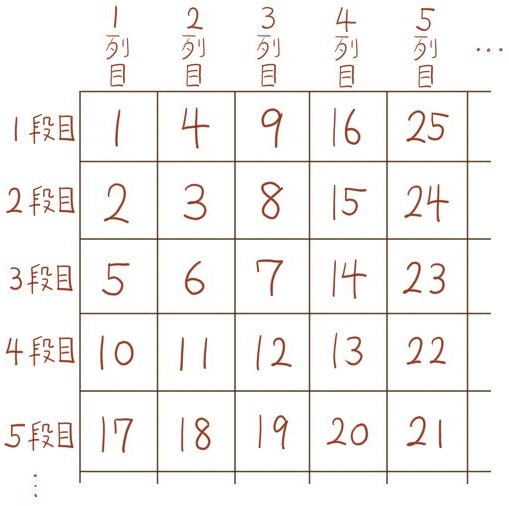
(1) ２段目の８列目の数を求めよ。
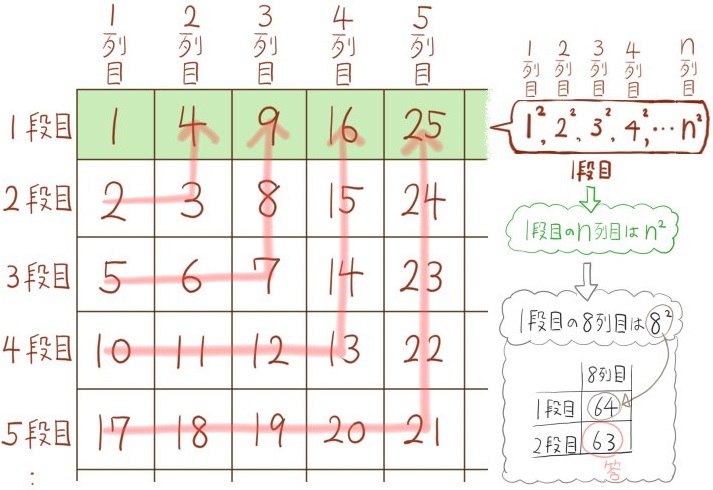
(2) ８段目の１列目の数を求めよ。
(3) 103は何段目の何列目か。
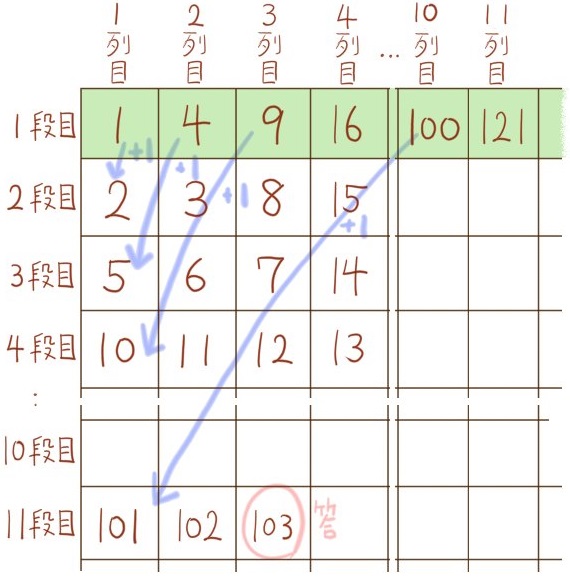
n段目のn列目の数を、nを使って表すと、その式はどうなるでしょうか。
