- 「2次方程式を解け」のパターンの難問
- 2次方程式の解から定数を求める難問
- 1つの2次方程式が登場する様々なパターン
- 2つの2次方程式が登場する難問
「2次方程式を解け」のパターンの難問|高校入試
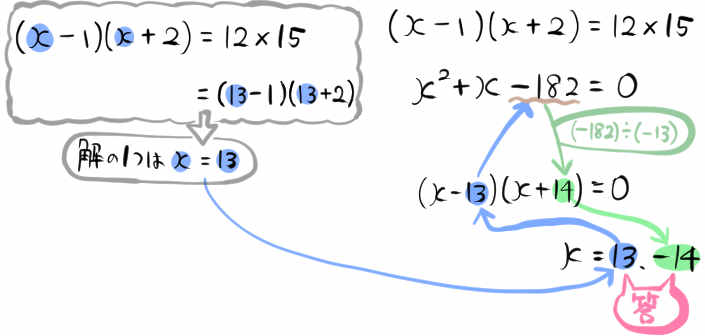
2次方程式 \(\left( x-1\right) \left( x+2\right) =12\times 15\) を解きなさい。
なぜ \(12\times 15\) の形で出題されているのか?と、疑問をいだくことが、問題制作者の意図に気が付くポイントです。
2次方程式 \(\left( x-\sqrt{2}\right) ^{2}-5\left( x-\sqrt{2}\right) +6=0\) を解きなさい。
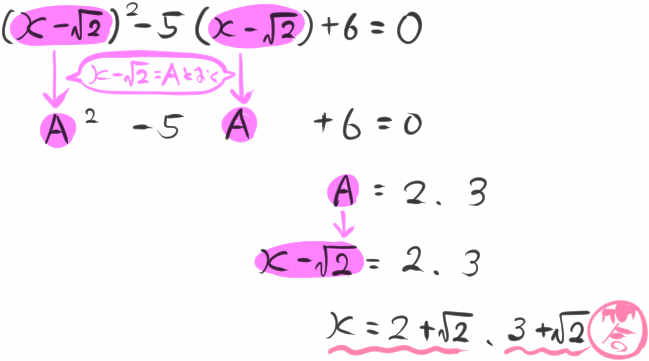
式のなかに同じかたちのかたまりがあれば、文字に置き変えます。
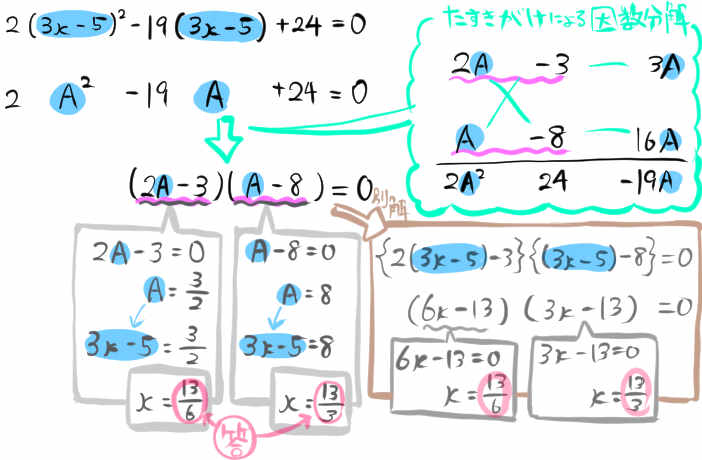
方程式 \(2\left( 3x-5\right) ^{2}-19\left( 3x-5\right) +24=0\) を解け。
この2次方程式の解を求めなさい。
![]()

式のなかに似たようなかたちがありますので、『式変形で同じかたちを作り出し、文字に置き換えることができないか』を考えます。
2次方程式の解から定数を求める難問

\(x\) の2次方程式 \(x^{2}-2x+1-2a=0\) の1つの解が \(x=1+\sqrt{2}\) であるとき、定数aの値を求めなさい。
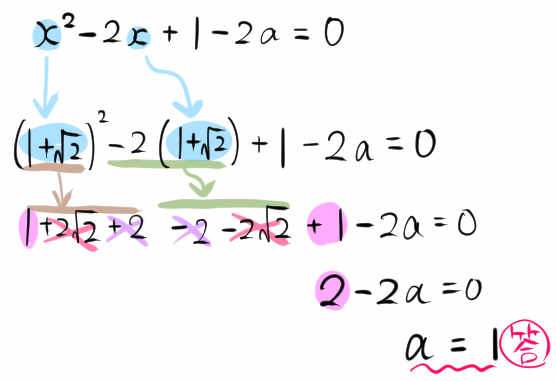
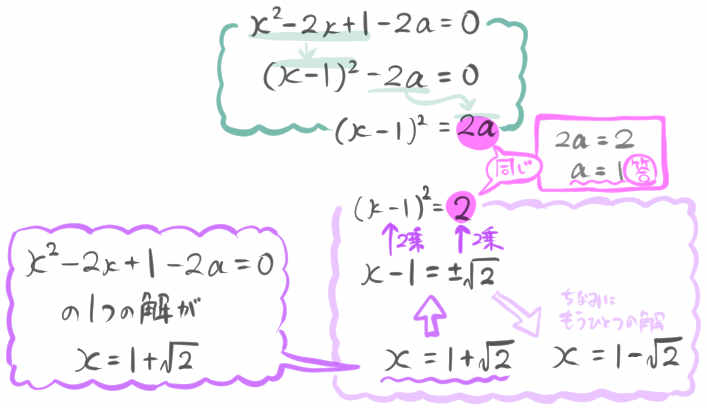
xについての2次方程式の解をxに代入すると、等式が成り立ちます。
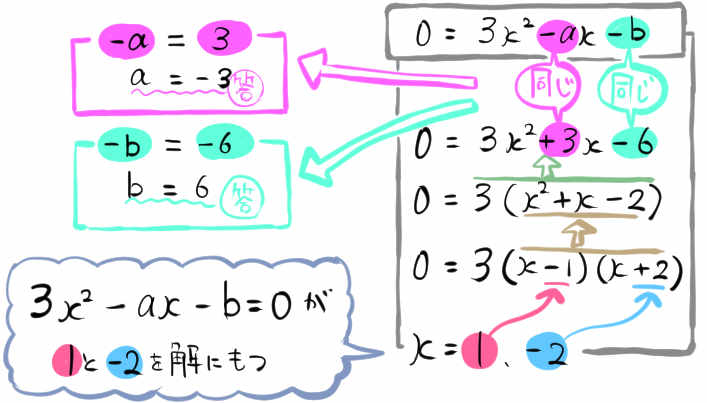
\(x\) の2次方程式 \(3x^{2}-ax-b=0\) が1と-2を解にもつとき、定数a,bの値を求めなさい。
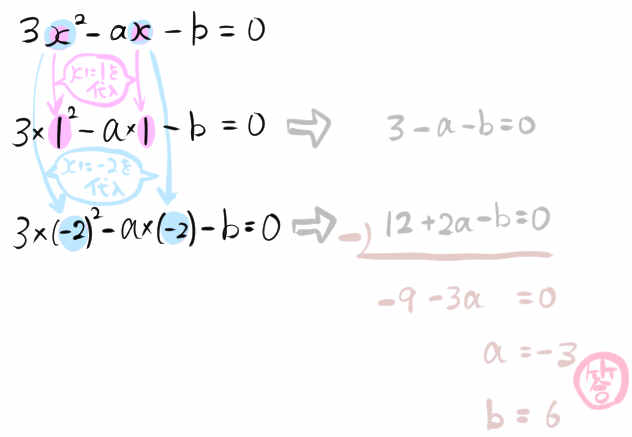
\(x\) についての2次方程式 \(x^{2}-3ax+\left( a+1\right) \left( a-6\right) =0\) の解の1つが\(a-2\) であるとき、
aの値を求めなさい。
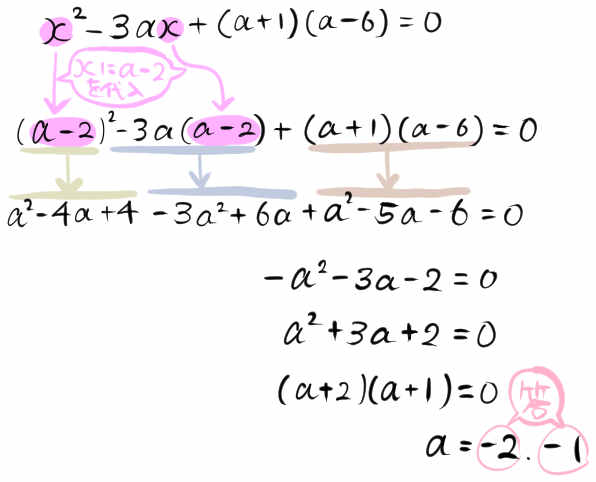
aを正の定数とする。
\(x\) の2次方程式 \(x^{2}+\left( 2a+1\right) x-4a^{2}+2=0\) の解の1つがaであるとき、aの値と、もう一つの解を求めなさい。

\(x\) の2次方程式 \(x^{2}+ax-20=0\) が2つの整数の解を持つとき、aのとりうる値をすべて求めなさい。
次のように、かけて-20になる整数Aと整数Bの組み合わせを考えます。
A+Bの値がaの値なので、それを答えます。
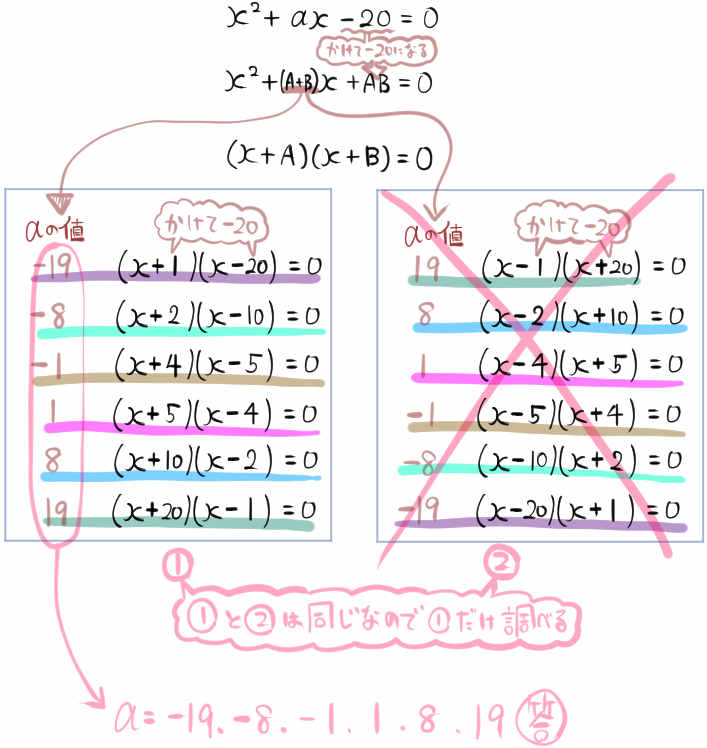
解が整数となる場合は、2次方程式の左辺が因数分解された形を予想するのが有効な手のひとつです。
\(x\) の2次方程式 \(x^{2}+ax+12=0\) の2つの解がともに負の整数であるようなaの値をすべて求めなさい。
かけて12になる2つの正の整数の組み合わせ(緑の数字の部分)を探すことになります。
1と12
2と6
3と4
この3パターンが存在します。

\(x\) についての2次方程式 \(x^{2}-2\left( a+6\right) x+a^{2}+8a=0\) の解が \(x=-3\) のみのとき、aの値を求めなさい。
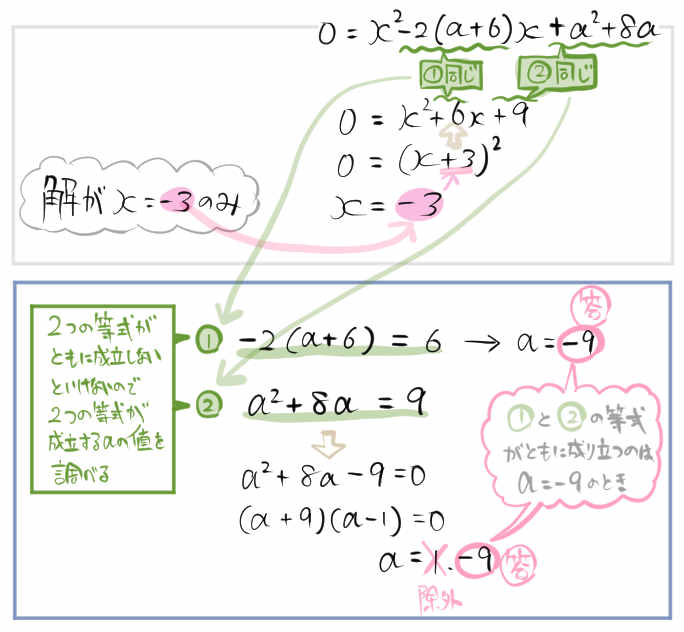

解が \(x=-3\) のみとならない場合を除外するチェックが必要です。
\(x\) の2次方程式 \(ax^{2}+bx-33=0\) は異符号の2つの解c.dを持ち、 \(c-d=\dfrac{7}{2}\) で、その絶対値の比は \(\left| c\right| :\left| d\right| =11:3\) である。
a.bの値を求めよ。
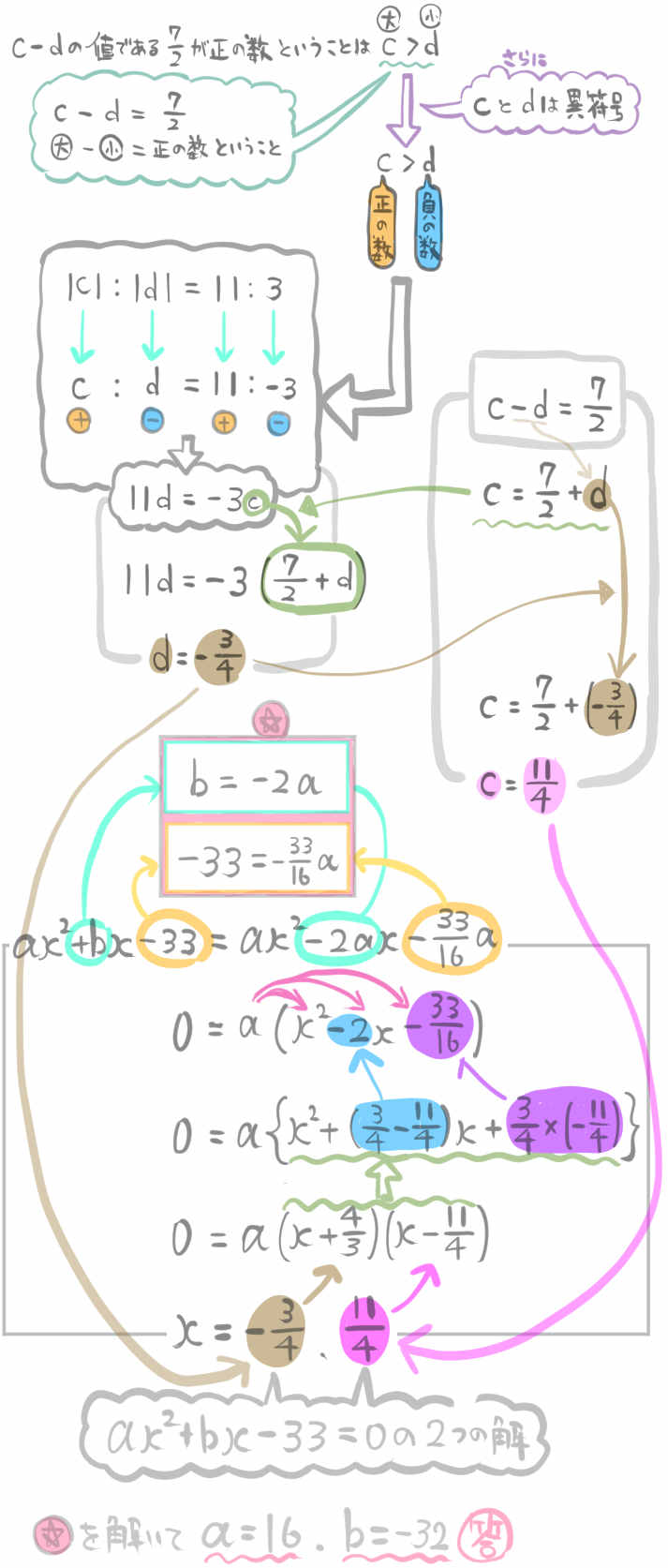
\(c-d=\dfrac{7}{2}\)つまり正の数になるということは、cとdのどちらが大きい数でしょうか。
その他、1つの2次方程式が登場する難問いろいろ
2次方程式 \(x^{2}-4x-3=0\) の正の解をaとするとき
\(a^{2}-3a+4-\sqrt{7}\) の値を求めなさい。

2次方程式 \(\left( x+3\right) ^{2}+\left( x+3\right) \left( x-3\right) =1\) の2つの解の差の2乗の値を求めよ。
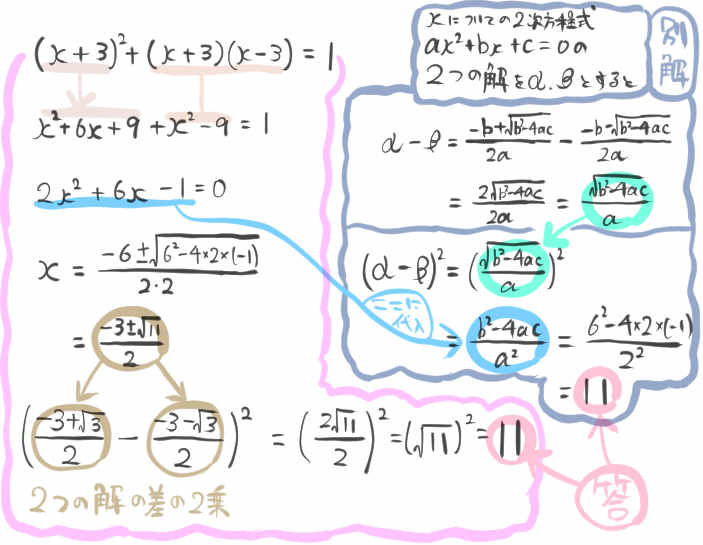
2つの解を求め、その差の2乗をする、という手順を踏むだけですが、2通りの手順を紹介しています。
2次方程式 \(x^{2}+ax+3=0\) の2つの解の差は \(2\sqrt{6}\) である。aの値を求めなさい。
解の公式を使い、2つの解について定数aを含む式で表します。

まず、2つの解について定数aを含む式で表します。
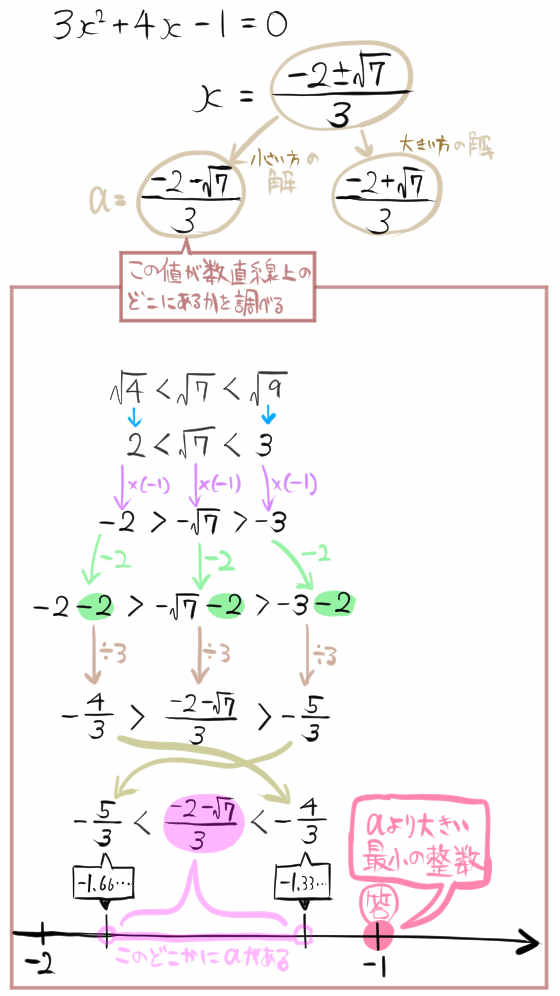
2次方程式 \(3x^{2}+4x-1=0\) の2解のうち、小さい方をaとする。
aよりも大きい最小の整数を求めなさい。
\(x\) の2次方程式
\({\small x^{2}-\left( a^{2}-4a+5\right) x+5a\left( a-4\right) =0}\)
において、aが正の整数であるとき、次の(1),(2)の問いに答えなさい。
(1) この2次方程式の解が1つになるようなaの値を求めよ。


(明治高校)
与えられた式をよく観察して、解説にあるような式変形に気が付けば、スムーズに解答できます。
2つの2次方程式が登場する難問|高校入試問題
\(x\) の2次方程式 \(x^{2}+ax+6=0\) の解の1つは2であり、もう1つの解は
\(x\) の1次方程式 \(ax+b=0\) の解になっている。
このとき、aとbの値を求めよ。
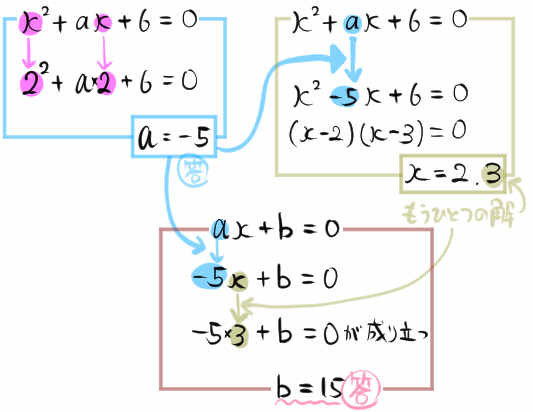
解の1つが2であるということは、\(x\) の2次方程式のxに2を代入すると、その等式が成り立つということです。それをaについて解いてaの値を求めます。このように、できることを順番に済ませてゆくと、一つひとつ明らかになっていきます。
\(x\) の2次方程式 \(x^{2}+ax+b=0\) の解が-3と2のとき
\(t\) の2次方程式 \(t^{2}+bt+a=-4\) を解きなさい。
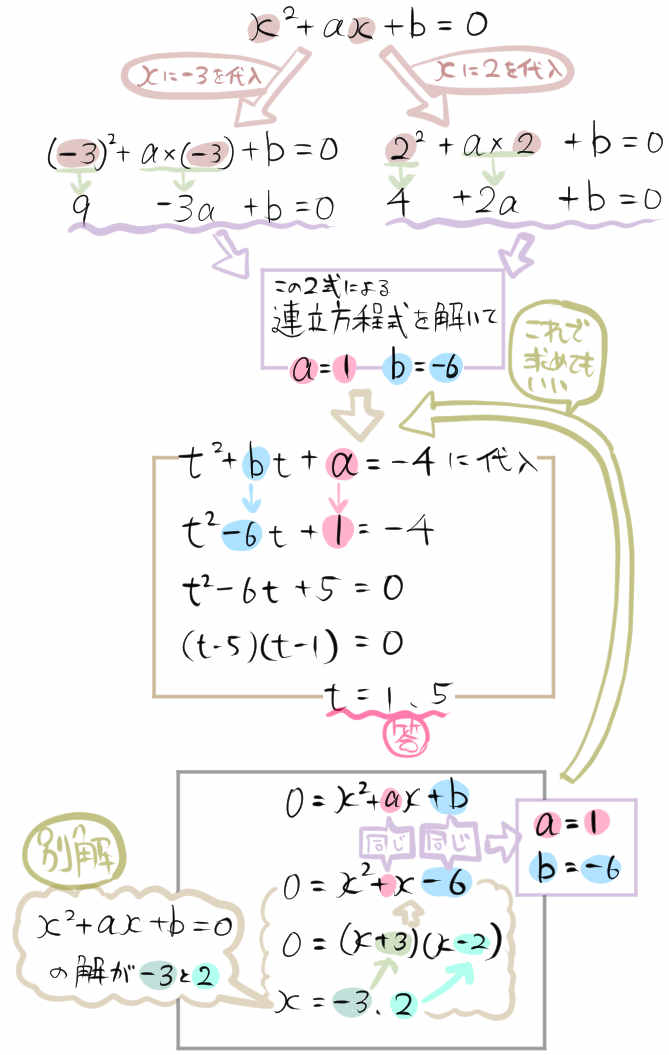
まず前者の式から、aとbを求めます。
\(x\) の2次方程式 \(x^{2}+ax+b=0\) の2つの解の逆数が
\(x\) の2次方程式 \(x^{2}-5x+6=0\) の解となる
aとb値をそれぞれ求めなさい。
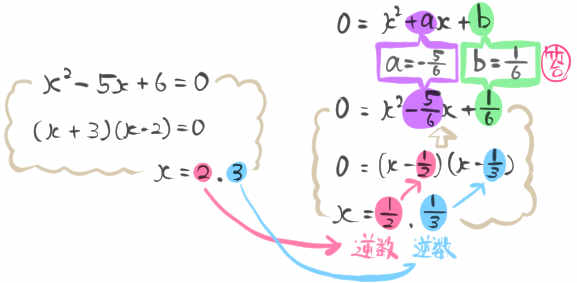
後者の方程式の解の逆数もまた、前者の方程式の解の逆数となります。
2次方程式 \(x^{2}-5x+3=0\) の2つの解からそれぞれ2を引くと
2次方程式 \(x^{2}+ax+b=0\) の解になるとき
a,bの値をそれぞれ求めよ。
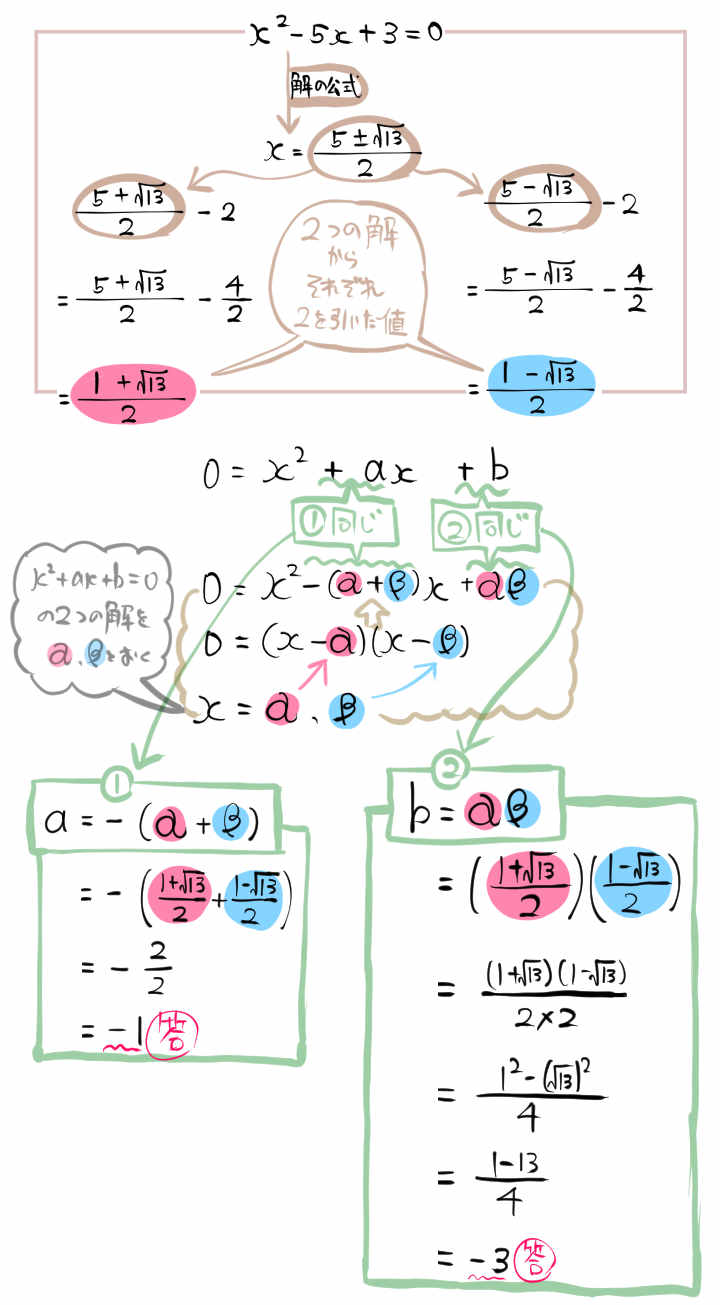

前者の方程式の解を文字におくと、後者の方程式の解はそこから2を引いたものとして表すことができます。
\(x\) についての2次方程式 \(x^{2}+ax+b=0\) の2つの解からそれぞれ1を引いて2倍した数が
\(x\) についての2次方程式 \(x^{2}-6x+4=0\) の2つの解になっている。
a,bの値を求めよ。
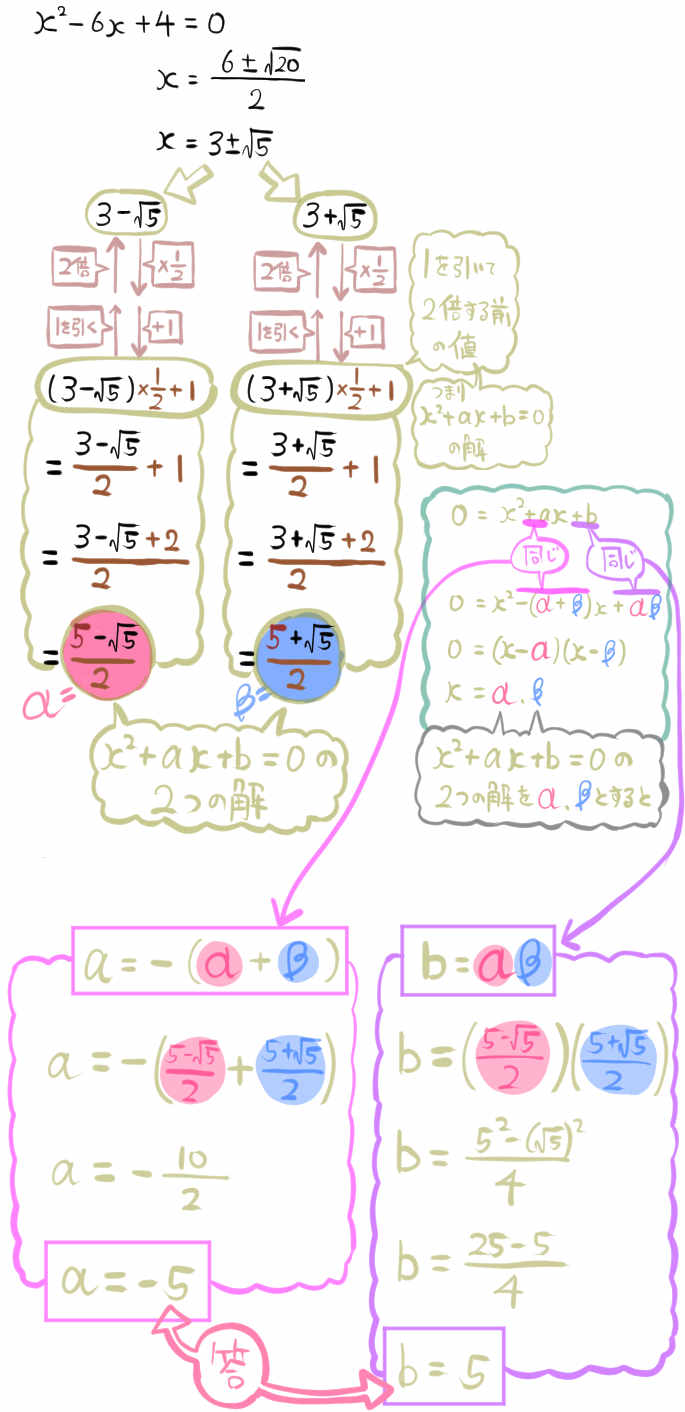
1を引いて2倍するという操作の逆を考えます。つまり、後者の式の解に対して、半分にして1を加えた数が、前者の式の解になります。
2次方程式 \(x^{2}+ax+b=0\) の2つの解にそれぞれ3を足したものは
2次方程式 \(x^{2}+bx+a=0\) の解になるという。
定数aとbの値をそれぞれ求めなさい。
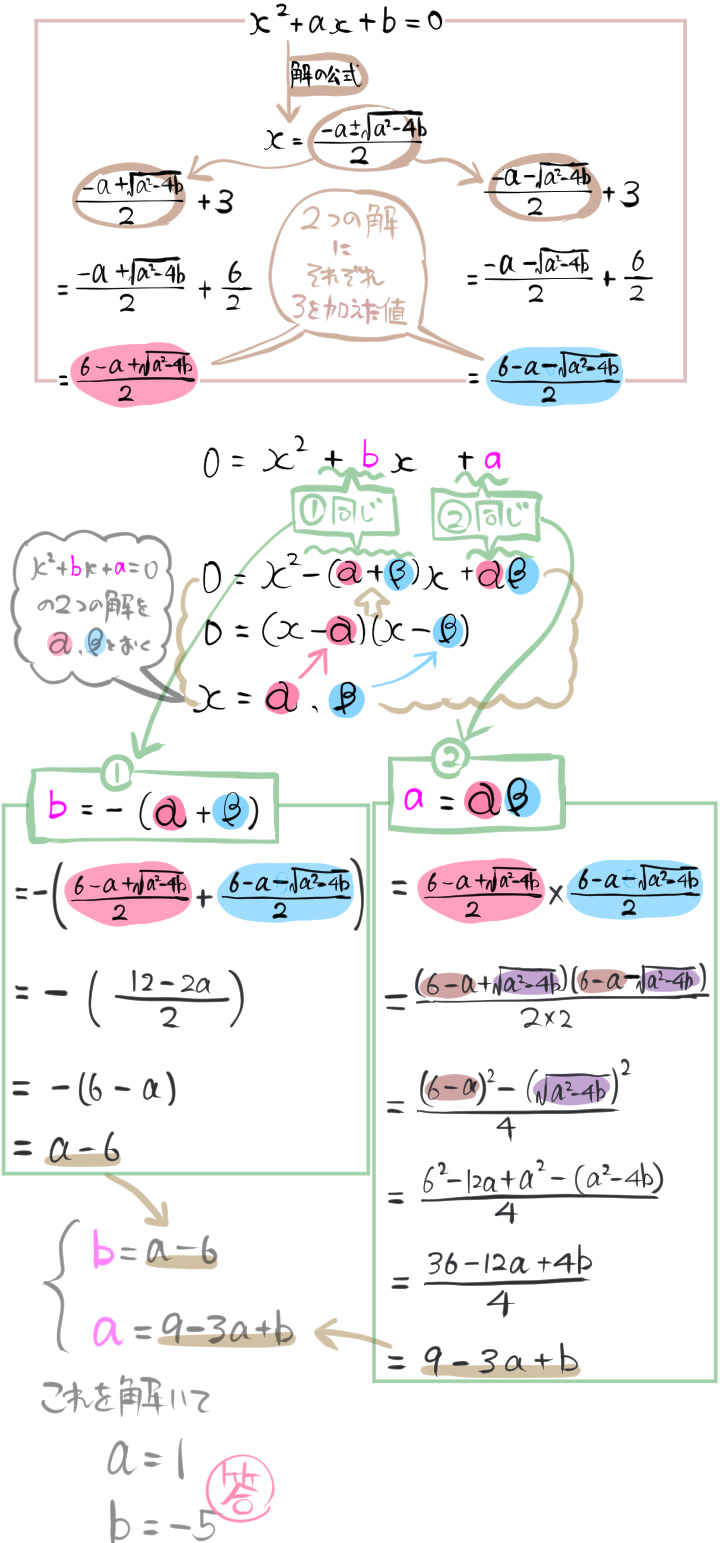
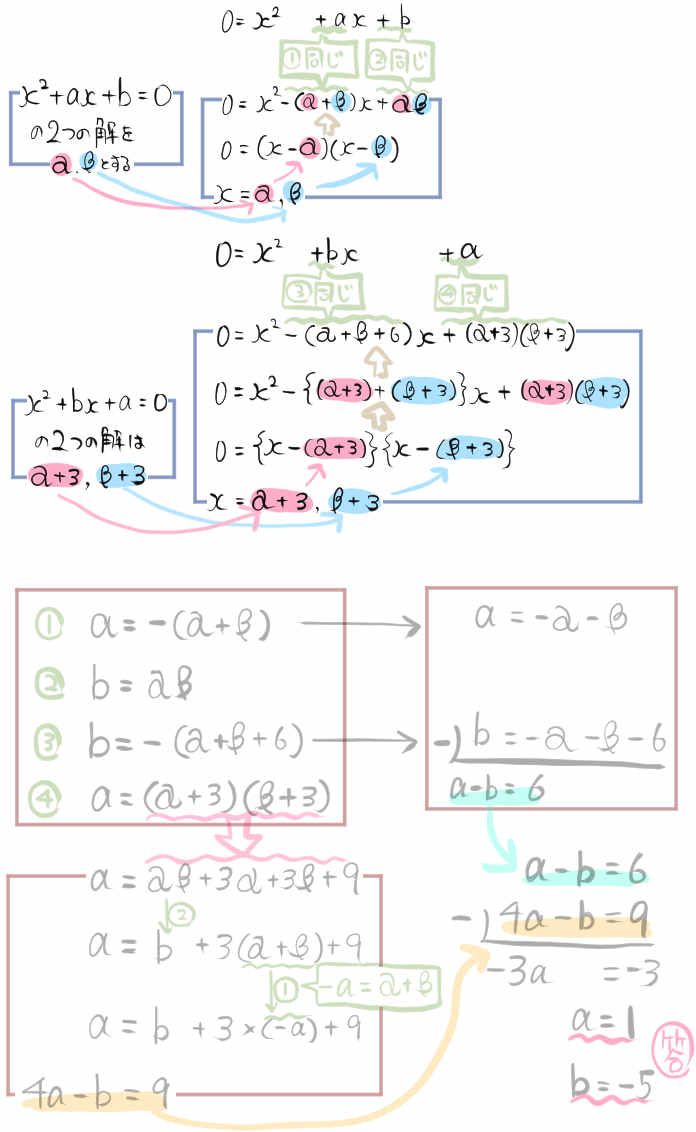
- 基本~難問『2次方程式の利用』
- 2次方程式の面白い問題
- 難問『因数分解』
- 因数分解の文章問題