


- 分数のある等式の変形の基本問題|定期テスト対策用
- 等式の変形の標準問題から、やや難しい応用問題まで
- 等式の変形の応用問題|高校入試の難問
分数のある等式の変形の基本問題|定期テスト対策用


等式を変形し、bについて解きなさい。
\(\dfrac{a}{2}-\dfrac{b}{3}=1\)
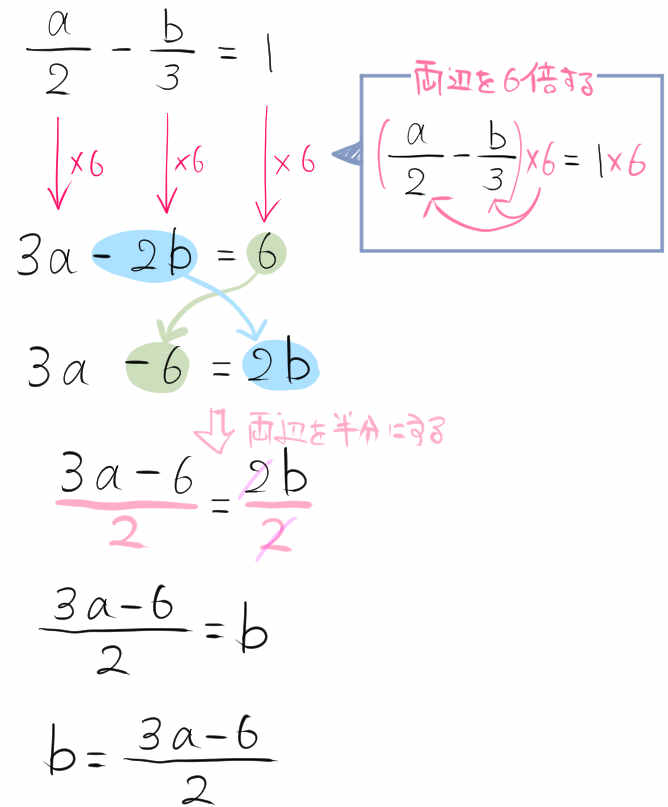
等式を変形し、bについて解きなさい。
\(a=\dfrac{2b-c}{7}\)
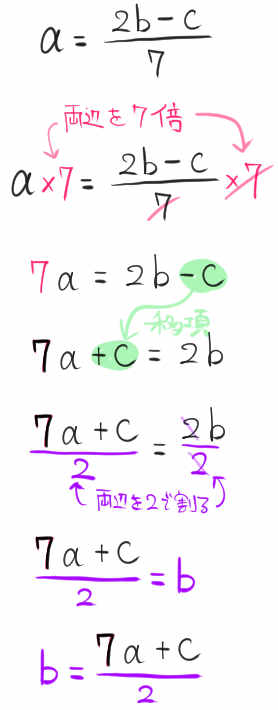
等式を変形し、cについて解きなさい。
\(a=\dfrac{1}{b}+\dfrac{c}{4}\)
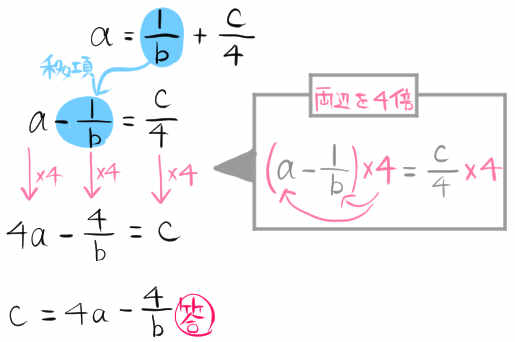
等式を変形し、cについて解きなさい。
\(a=\dfrac{c}{b}+d\)
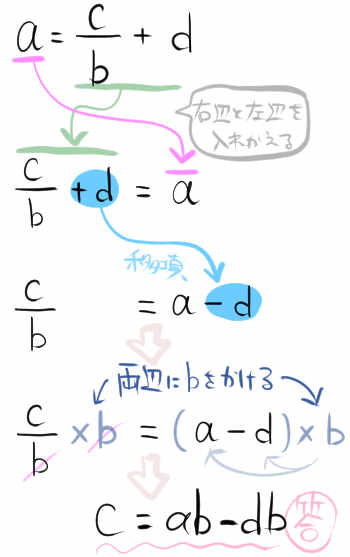
等式を変形し、bについて解きなさい。
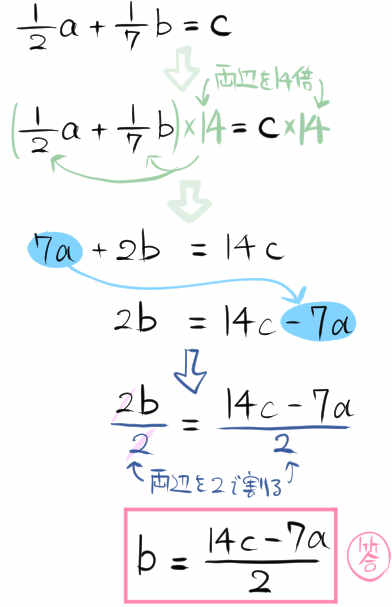
\(\dfrac{1}{2}a+\dfrac{1}{7}b=c\)
等式を変形し、yについて解きなさい。
\(2a=\dfrac{x\left( y-1\right) }{b}\)

等式の変形の問題|標準~やや難しい応用問題
等式を変形し、bについて解きなさい。
\(1.25a+0.25b=0.5\)
別解のように、各項の係数が0.25の倍数だと気が付くとスムーズに解けます。
しかし、気が付かなくても、両辺を100倍して解いていけば大丈夫です。
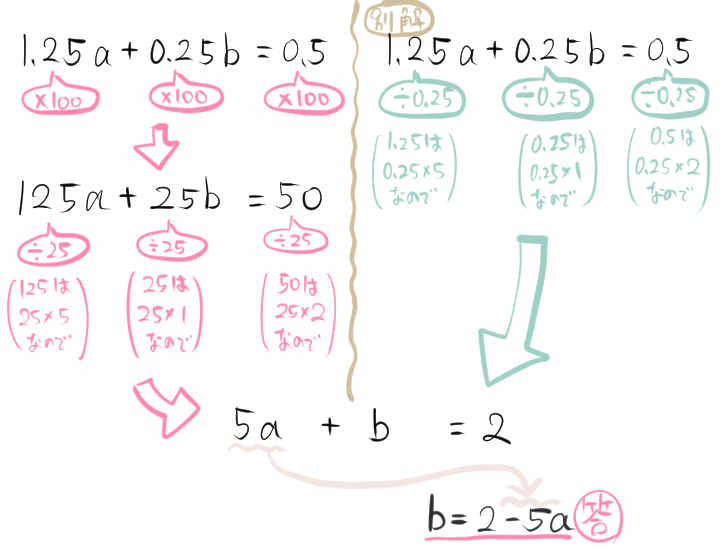
等式の変形で小数がある場合は、両辺を何倍かして、等式の係数を整数にします。ただ、別解のように解く方法もあります。
等式を変形し、yについて解きなさい。
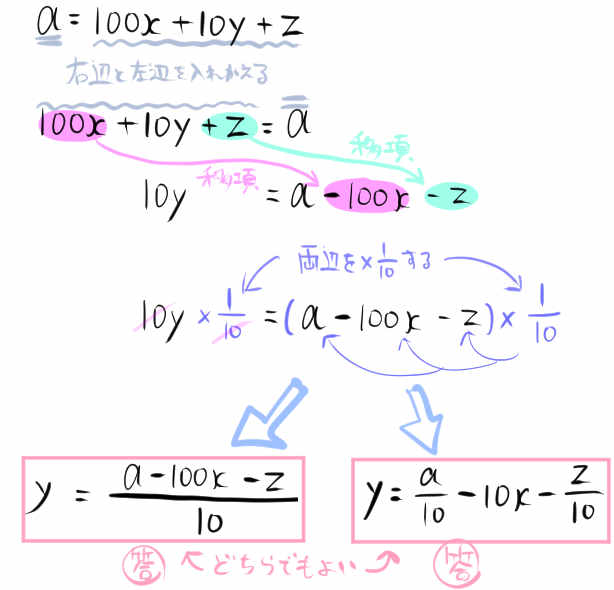
\(a=100x+10y+z\)
等式を変形し、 \(l\) について解きなさい。
\(S=\pi r^{2}+\pi lr\)

等式を変形し、aについて解きなさい。
\(\dfrac{a}{b}=\dfrac{2a+3b}{5}\)
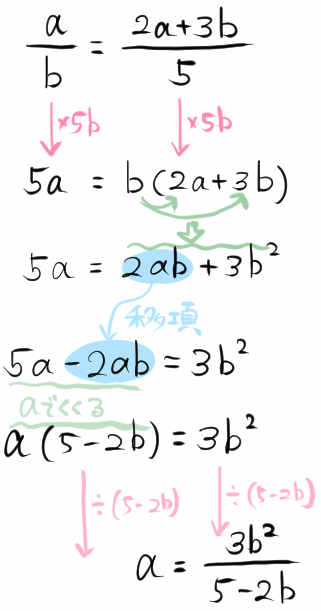
aについて解くように指示があるので、まずaのついている項をまとめます。
等式を変形し、aについて解きなさい。
\(x=\dfrac{5}{a}-\dfrac{7}{b}\)
まず、両辺にabをかけます。
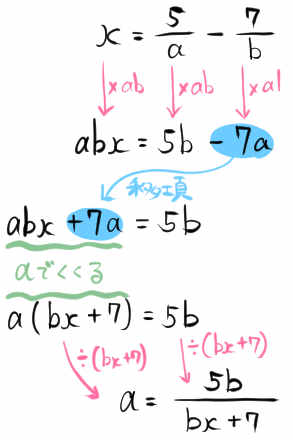
分母の文字を消すために両辺に何をかければいいかと考えます。
等式を変形し、aについて解きなさい。
\(\dfrac{1}{2a}-\dfrac{2}{b}=c\)
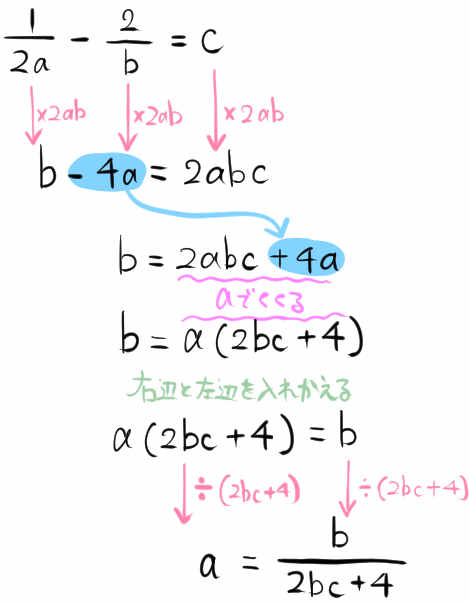
等式を変形し、aについて解きなさい。
\(x=\dfrac{1}{2}\left( a+b\right) c\)
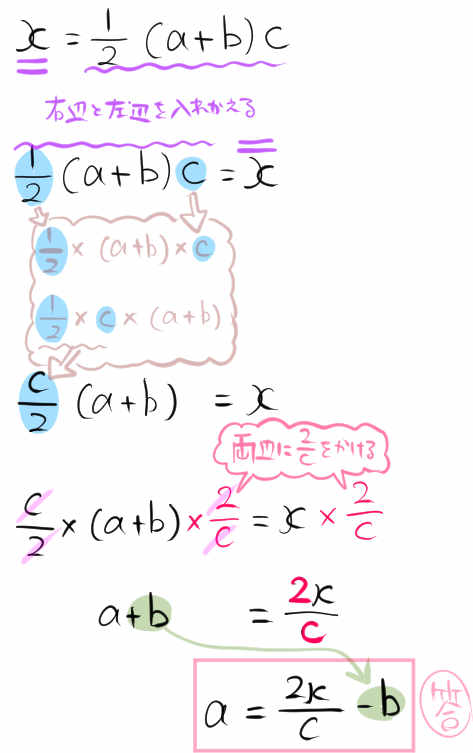
解説では、\(\dfrac{1}{2}\)と \(c\) をまとめていますが、ひとつずつ消すことを考えてもOKです。
等式を変形し、bについて解きなさい。
\(x=\left( 3a-2b+c\right) y\)
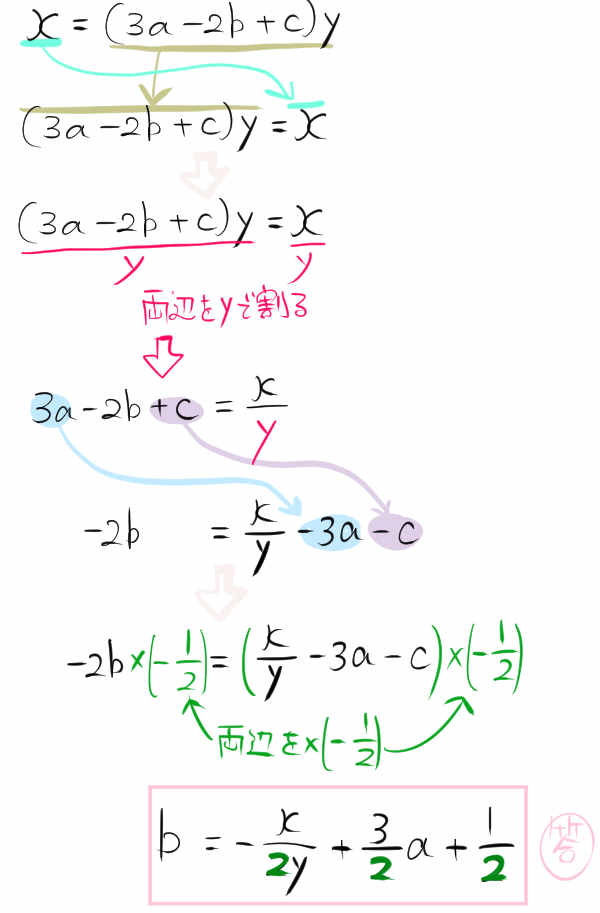
等式の変形の応用問題|高校入試の難問
等式を変形し、xについて解きなさい。
\(\dfrac{1}{x}=\dfrac{1}{y}+\dfrac{1}{z}\)
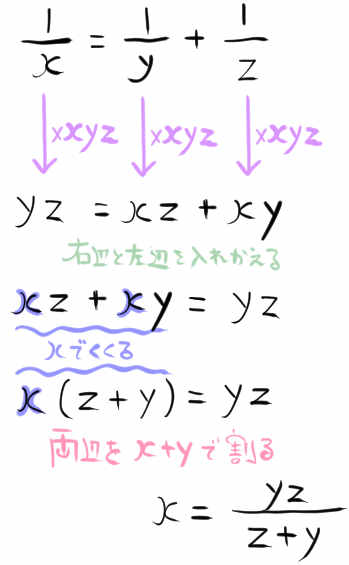
等式を変形し、xについて解きなさい。
\(y=\dfrac{7x+5}{2x-3}\)
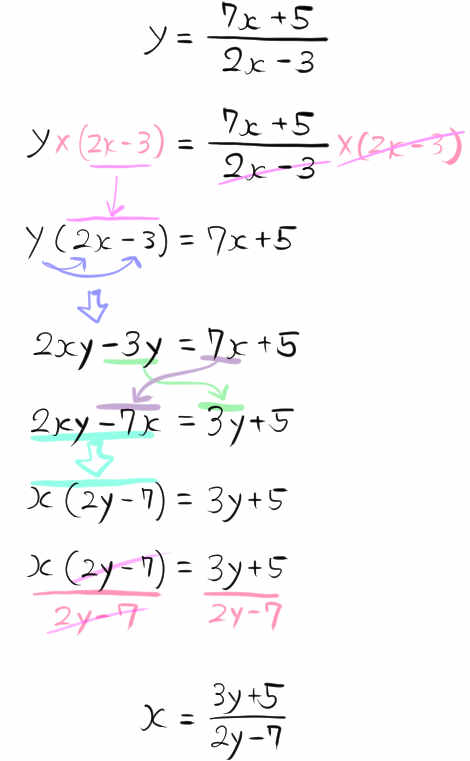
分母の式をどう処理するかがポイントです。このページでは初めて見る変形なので、少し考えてわからない場合は解き方を見ましょう。
等式を変形し、cについて解きなさい。
\(\dfrac{a\left( c-d\right) }{c+d}+\dfrac{b\left( c+d\right) }{c-d}=a+b\)

高校入試に出題された応用問題の難問です。中学3年生で学習する乗法公式も利用します。





























