

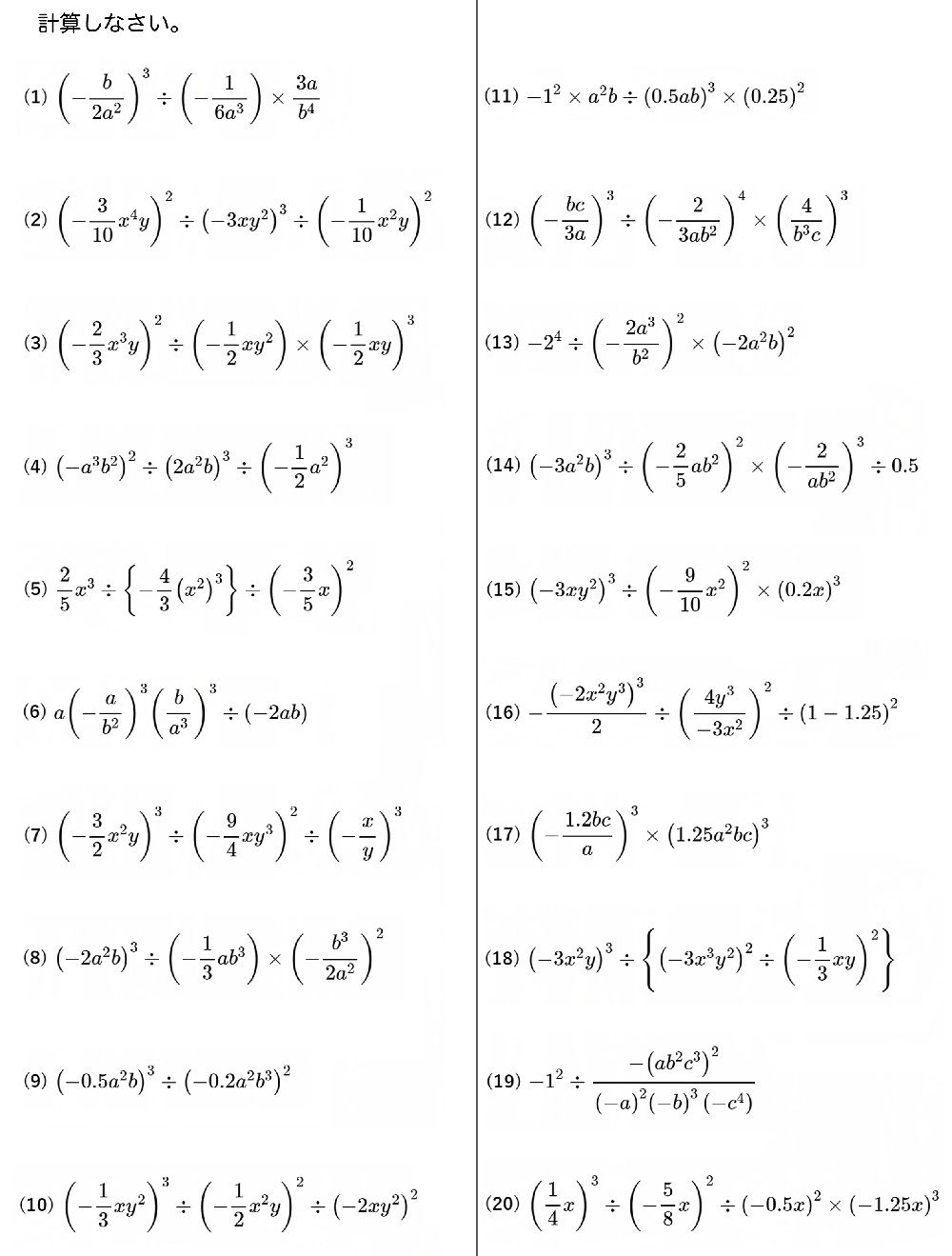

中2|単項式の乗除の難問たち
(1) \(\left( -\dfrac{b}{2a^{2}}\right) ^{3}\div \left( -\dfrac{1}{6a^{3}}\right) \times \dfrac{3a}{b^{4}}\)
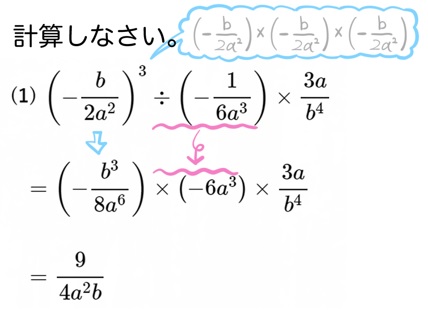
(2) \({\small \left( -\dfrac{3}{10}x^{4}y\right) ^{2}\div \left( -3xy^{2}\right) ^{3}\div \left( -\dfrac{1}{10}x^{2}y\right) ^{2}}\)
(3) \({\small \left( -\dfrac{2}{3}x^{3}y\right) ^{2}\div \left( -\dfrac{1}{2}xy^{2}\right) \times \left( -\dfrac{1}{2}xy\right) ^{3}}\)

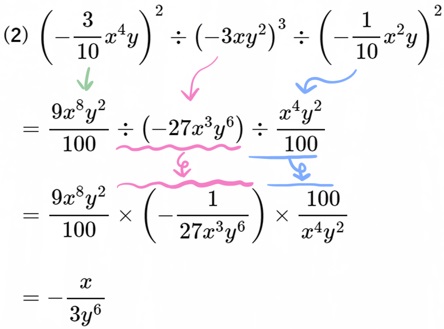
(4) \(\left( -a^{3}b^{2}\right) ^{2}\div \left( 2a^{2}b\right) ^{3}\div \left( -\dfrac{1}{2}a^{2}\right) ^{3}\)
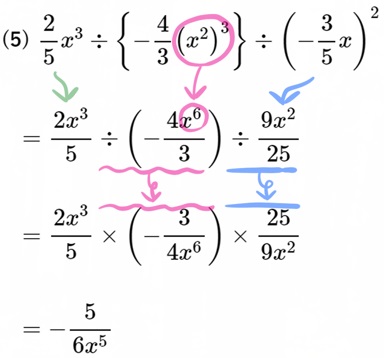
(5) \(\dfrac{2}{5}x^{3}\div \left\{ -\dfrac{4}{3}\left( x^{2}\right) ^{3}\right\} \div \left( -\dfrac{3}{5}x\right) ^{2}\)
(6) \(a\left( -\dfrac{a}{b^{2}}\right) ^{3}\left( \dfrac{b}{a^{3}}\right) ^{3}\div \left( -2ab\right) \)
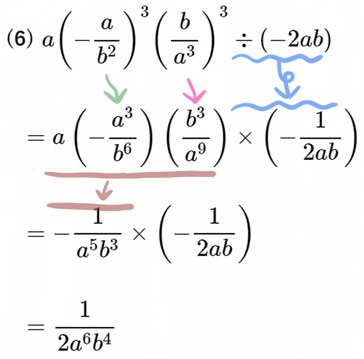
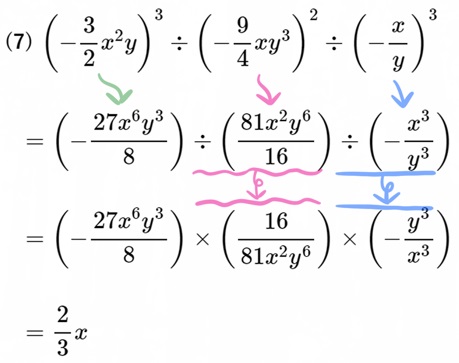
(7) \(\left( -\dfrac{3}{2}x^{2}y\right) ^{3}\div \left( -\dfrac{9}{4}xy^{3}\right) ^{2}\div \left( -\dfrac{x}{y}\right) ^{3}\)
(8) \(\left( -2a^{2}b\right) ^{3}\div \left( -\dfrac{1}{3}ab^{3}\right) \times \left( -\dfrac{b^{3}}{2a^{2}}\right) ^{2}\)
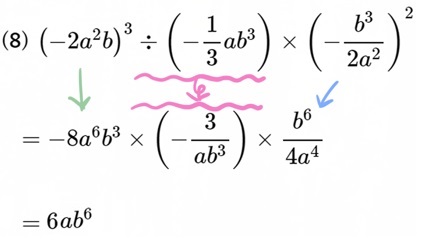
(9) \(\left( -0.5a^{2}b\right) ^{3}\div \left( -0.2a^{2}b^{3}\right) ^{2}\)
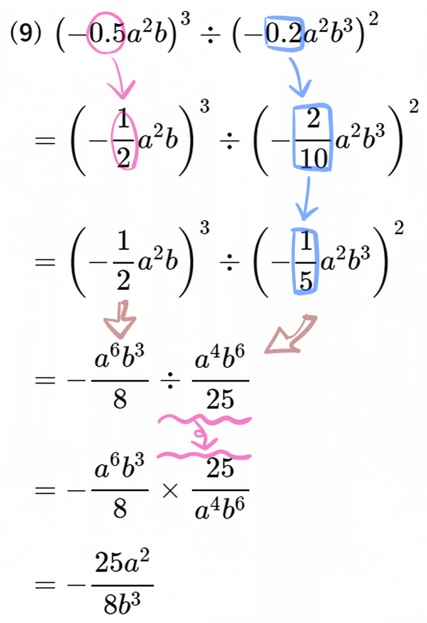
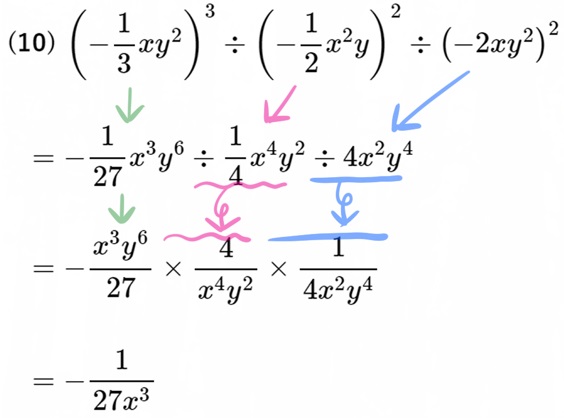
(10) \(\left( -\dfrac{1}{3}xy^{2}\right) ^{3}\div \left( -\dfrac{1}{2}x^{2}y\right) ^{2}\div \left( -2xy^{2}\right) ^{2}\)
(11) \(-1^{2}\times a^{2}b\div \left( 0.5ab\right) ^{3}\times \left( 0.25\right) ^{2}\)

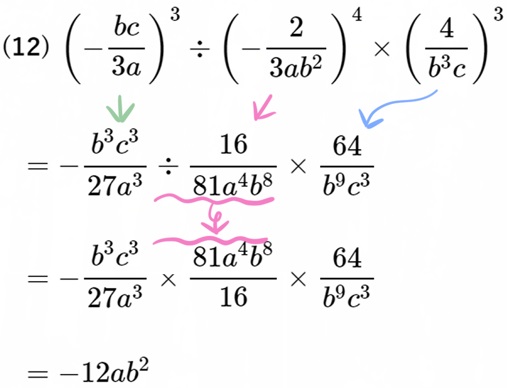
(12) \(\left( -\dfrac{bc}{3a}\right) ^{3}\div \left( -\dfrac{2}{3ab^{2}}\right) ^{4}\times \left( \dfrac{4}{b^{3}c}\right) ^{3}\)
(13) \(-2^{4}\div \left( -\dfrac{2a^{3}}{b^{2}}\right) ^{2}\times \left( -2a^{2}b\right) ^{2}\)
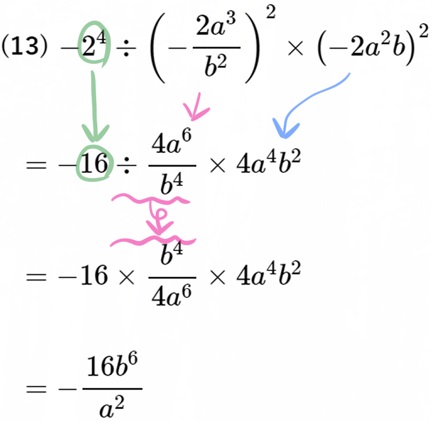
(14) \({\small \left( -3a^{2}b\right) ^{3}\div \left( -\dfrac{2}{5}ab^{2}\right) ^{2}\times \left( -\dfrac{2}{ab^{2}}\right) ^{3}\div 0.5}\)
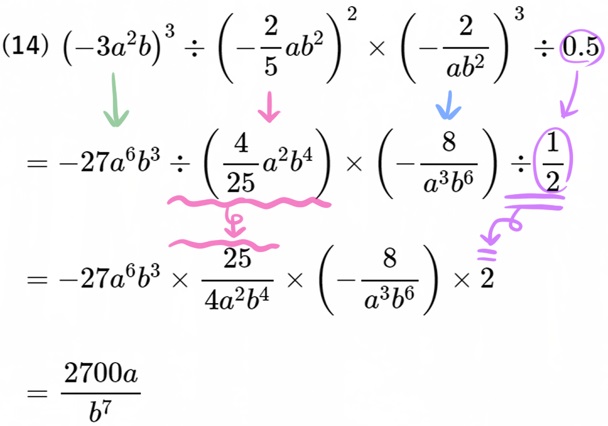
(15) \(\left( -3xy^{2}\right) ^{3}\div \left( -\dfrac{9}{10}x^{2}\right) ^{2}\times \left( 0.2x\right) ^{3}\)

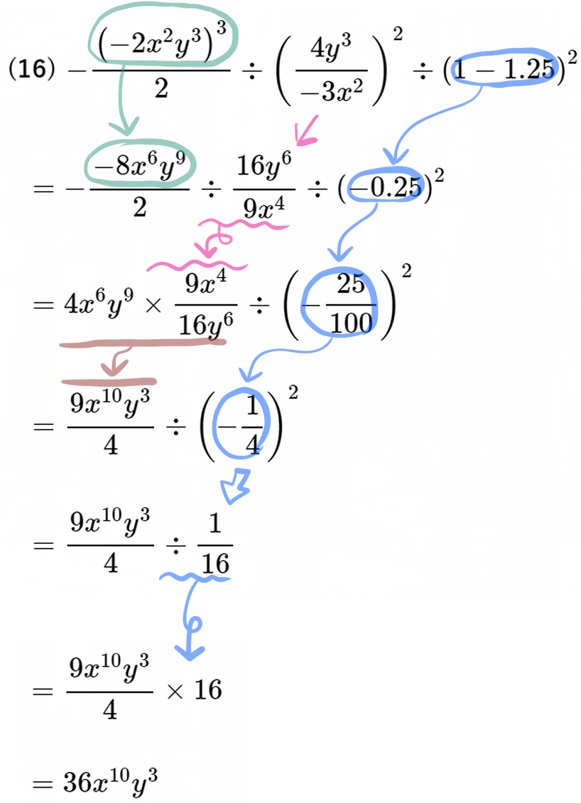
(16) \({\small -\dfrac{\left( -2x^{2}y^{3}\right) ^{3}}{2}\div \left( \dfrac{4y^{3}}{-3x^{2}}\right) ^{2}\div \left( 1-1.25\right) ^{2}}\)
(17) \(\left( -\dfrac{1.2bc}{a}\right) ^{3}\times \left( 1.25a^{2}bc\right) ^{3}\)

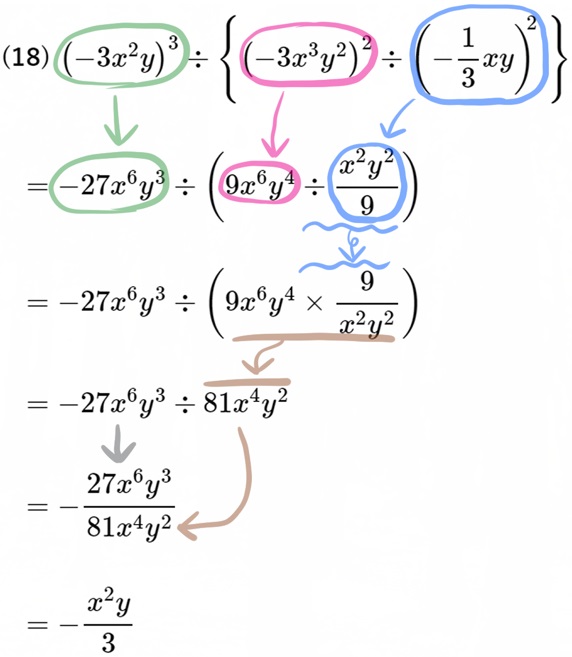
(18) \({\small \left( -3x^{2}y\right) ^{3}\div \left\{ \left( -3x^{3}y^{2}\right) ^{2}\div \left( -\dfrac{1}{3}xy\right) ^{2}\right\} }\)
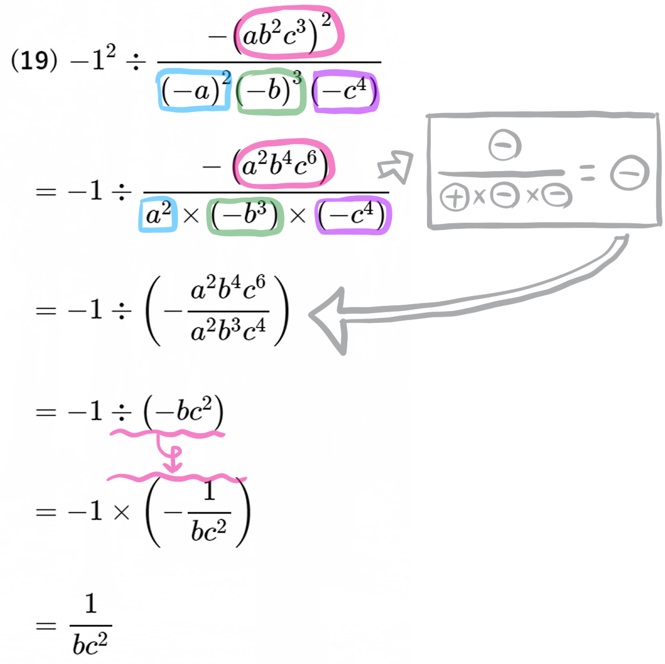
(19) \(-1^{2}\div \dfrac{-\left( ab^{2}c^{3}\right) ^{2}}{\left( -a\right) ^{2}\left( -b\right) ^{3}\left( -c^{4}\right) }\)
(20) \({\small \left( \dfrac{1}{4}x\right) ^{3}\div \left( -\dfrac{5}{8}x\right) ^{2}\div \left( -0.5x\right) ^{2}\times \left( -1.25x\right) ^{3}}\)


※セット版も単品版もあります。










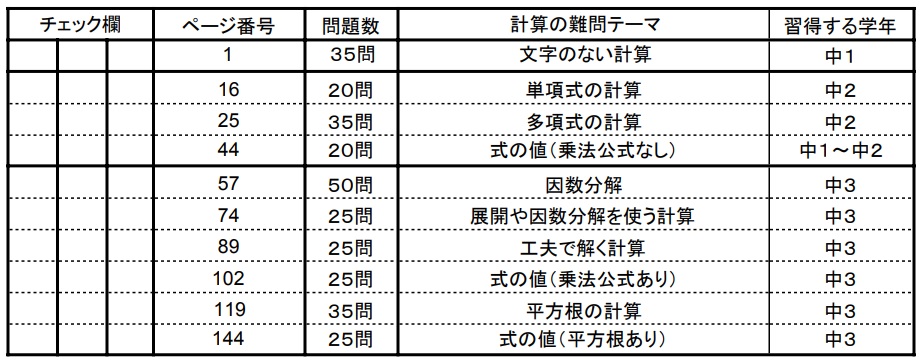
- 文字のない計算(正負の数の計算問題・四則演算)
- 単項式の計算(単項式の乗除)(←このページ)
- 多項式の計算問題の難問
- 式の値(乗法公式なし)
- 因数分解の難問
- 展開や因数分解を使う計算(多項式の計算)
- 工夫で解く計算問題
- 式の値(乗法公式あり)
- 平方根の計算問題の難問
- 式の値(平方根あり)

単項式の乗除の難問を計算する際に小数が出た場合の処理
小数から分数への変換は、代表的なものは暗記しておいてもいいでしょう。
とりあえずよく登場するは0.25の倍数です。
\(0.25=\dfrac{25}{100}=\dfrac{1}{4}\)
\(0.75=\dfrac{75}{100}=\dfrac{3}{4}\)
\(1.25=\dfrac{125}{100}=\dfrac{5}{4}\)
\(1.75=\dfrac{175}{100}=\dfrac{7}{4}\)
約分の際に25が何個あるかを意識して約分するといいでしょう。
単項式の計算問題の難問の学習は以上になります。



























