



中2|多項式の計算問題の難問35パターン
(1) \(2\left( \dfrac{2a-3b}{6}\right) -8\left( \dfrac{3a-b}{4}\right) \)

(2) \(\dfrac{3x-2y+1}{2}+x-2y+1\)

(3) \(-\dfrac{2x-y}{6}+\dfrac{x-y}{9}-\dfrac{x-2y}{4}\)

(4) \(\dfrac{2x+y}{3}-\dfrac{x-2y}{2}-\dfrac{2x-3y}{6}\)

(5) \(\dfrac{4x-y}{12}-\left( \dfrac{2x-y}{6}-\dfrac{3x-5y}{4}\right) \)

(6) \(x-\left( \dfrac{3y-z}{4}-\dfrac{x-2y-3z}{6}\right) \)

(7) \(\dfrac{3a-4b-c}{2}-\left( a-\dfrac{2b-c}{3}\right) \)

(8) \(\dfrac{2\left( 3a-8b\right) }{7}-\dfrac{3\left( a-3b\right) }{2}\)

(9) \(\dfrac{2x\left( x-3y\right) }{3}-\dfrac{3y\left( 2x-y\right) }{2}-\dfrac{1}{6}x^{2}\)

(10) \(a-\dfrac{3\left( a-2b\right) }{2}-\dfrac{2}{3}b\)

(11) \(\dfrac{4}{3}\left( \dfrac{a-3b}{2}\right) -\dfrac{1}{3}\left( a-b\right) \)

(12) \(\dfrac{1}{4}\left( 2a-3b\right) -\dfrac{a-2b}{6}+\dfrac{a+3b}{3}\)

(13) \(\dfrac{2x+y}{3}-0.2x+y\)

(14) \(5x-3y-\dfrac{2x-y}{3}\times 5\)

(15) \(\dfrac{3x+2y}{3}-y-\dfrac{2x-y}{2}\)

(16) \(-\dfrac{3x+y}{2}-3x+2y-1\)

(17) \(\dfrac{5x-2y}{6}-3x+y-\dfrac{x-y}{4}\)

(18) \(\dfrac{2a-3b}{8}\times \left( -20\right) -\dfrac{a-b}{6}\times 36\)

(19) \(6\left( \dfrac{3a-b}{12}-\dfrac{a-b}{18}+a\right) \)

(20) \(\dfrac{2x-y-1}{6}-\dfrac{2}{3}\left( x-2\right) -\dfrac{x-3y+1}{2}\)

(21) \({\small 3\left( x-2y-1\right) -\dfrac{3x-y}{2}-\dfrac{1}{4}\left( x-y+1\right)} \)

(22) \(\dfrac{-\left( -2\right) ^{2}}{6}+144x^{6}y^{3}\div \left( -6x^{2}y\right) ^{3}\)

(23) \(\dfrac{1-2a}{5}-2\left( 1-3a\right) -\dfrac{1}{2}a\)

(24) \(\left( 1\div \dfrac{3}{x}\right) -3\times \dfrac{x-2y}{2}-y\)

(25) \(a-3b-\left\{ \dfrac{1}{4}a-\dfrac{1}{3}\left( a-2b\right) \right\} \)

(26) \(\dfrac{1}{6}x-\left( \dfrac{x-y}{8}-\dfrac{x-y}{9}\right) \times 12-y\)

(27) \({\tiny 3\left( \dfrac{a-2b}{2}-\dfrac{a+4b}{6}\right) -2\left( \dfrac{a-b}{2}-\dfrac{2a-b}{6}\right)} \)

(28) \({\tiny \left\{ \left( \dfrac{3x^{6}y^{3}}{2}\right) ^{2}-\dfrac{\left( 2x^{4}y^{2}\right) ^{3}}{7}\right\} \div \left( -\dfrac{1}{2}x^{2}y\right) ^{3}\times \left( \dfrac{xy^{2}}{31}\right) ^{2}}\)

(29) \(\left\{ \dfrac{1}{3}x^{2}y-\left( -3y\right) ^{2}\right\} \div \left( 1\div 0.3\right) ^{2}\div y\)

(30) \(\dfrac{2}{3}\left( 2a-\dfrac{1}{6}b\right) -\dfrac{1}{2}\left\{ \dfrac{5\left( a-b\right) }{3}\right\} \)

(31) \(6\left( \dfrac{1}{2}a^{2}-\dfrac{2}{3}a+0.5\right) -\dfrac{2}{3}\left( a^{2}-2\right) \)

(32) \(\dfrac{1}{0.2}\times \left\{ -\dfrac{1}{5}\left( a-b\right) -0.4a\right\} \)

(33) \(\left( \dfrac{a^{2}b}{0.25}\right) ^{2}-\left( 1\div \dfrac{1.5}{a}\right) ^{3}\div \left( a\div 3\right) ^{3}\)

(34) \(\dfrac{2a^{4}b-4a^{3}b^{2}}{2a^{2}b}-\dfrac{1.5a^{3}b^{2}-5a^{2}b^{3}}{3ab^{2}}\)


(35) \({\tiny \dfrac{x^{2}+3x^{2}y}{2}\div \left\{ \dfrac{15y^{2}+16}{8}-2\left( y^{2}+1\right) \right\} \div \left( -\dfrac{2x}{3y}\right) ^{2}}\)


※セット版も単品版もあります。










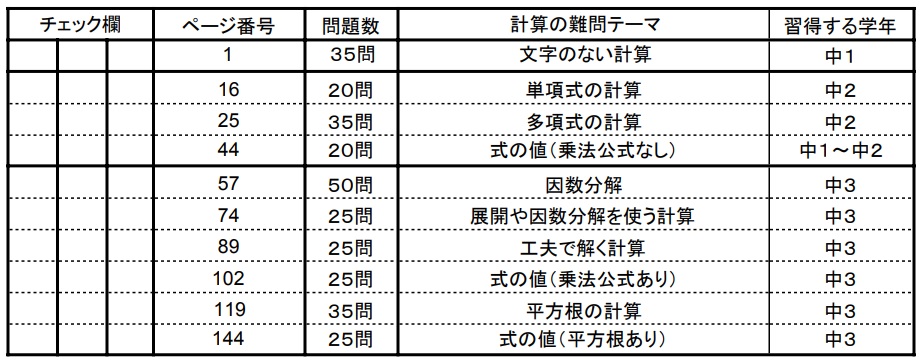
- 文字のない計算(正負の数の計算問題・四則演算)
- 単項式の計算(単項式の乗除)
- 多項式の計算問題の難問(←このページ)
- 式の値(乗法公式なし)
- 因数分解の難問
- 展開や因数分解を使う計算(多項式の計算)
- 工夫で解く計算問題
- 式の値(乗法公式あり)
- 平方根の計算問題の難問
- 式の値(平方根あり)




























