



- 相似比とは何か?三角形、四角形、円の3例で説明
- 円の相似比
- 相似比とは何かについてのまとめ(平面図形)
- 立体の相似比一覧|円錐や球、立方体など
- 相似比だと勘違いしやすい2辺の比との違い|両方使えると便利
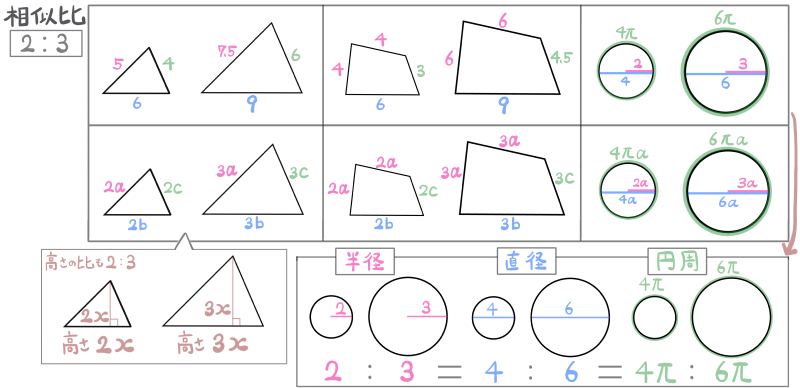
相似比とは何か?三角形、四角形、円の3例で説明
相似比とは、相似な図形の大きさの比率を表したものです。
大きさの比は、対応する部分の長さの比を調べると、それがそのまま大きさの比(相似比)になります。(まだ意味がわからなくてもOK)


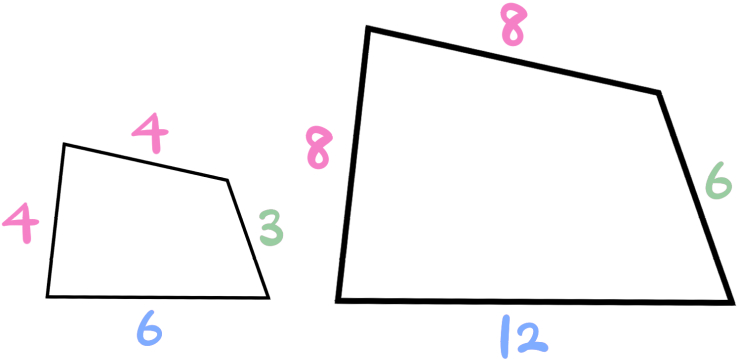
これもまた、各辺の長さが左と右で1:2になっています。
なので、左の四角形と右の四角形の相似比は1:2になります。
この四角形を使って、「各辺の長さは不明だけれど、相似比が1:2であることを表す図」を書くとこうなります。
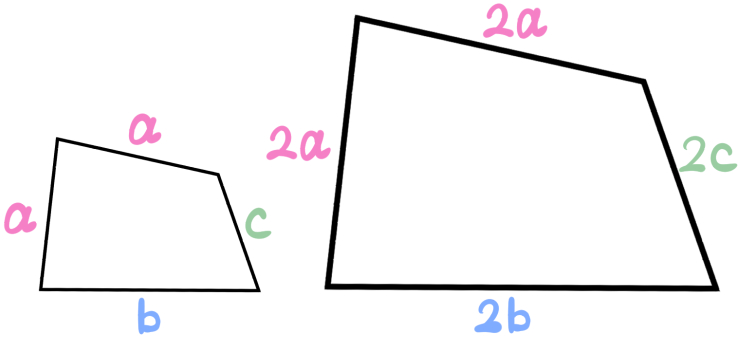
このように、同じ長さの辺には、同じ文字aを使います。

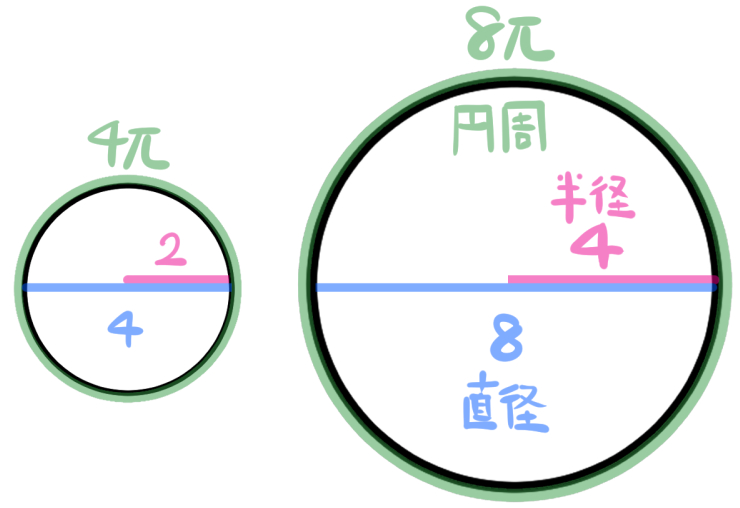
右の円の半径、直径、円周の長さが、左の円と比べてそれぞれ2倍になっています。
半径の長さの比は1:2
直径の長さの比は4:8(つまり1:2)
円周の長さの比は4π:8π(つまり1:2)

円の大きさの比率が左と右で1:2になっています。
なので、左の円と右の円の相似比は1:2です。
次に、「半径が不明だけれど、ともかく相似比が1:2になっている二つの円」を表すとこうなります。
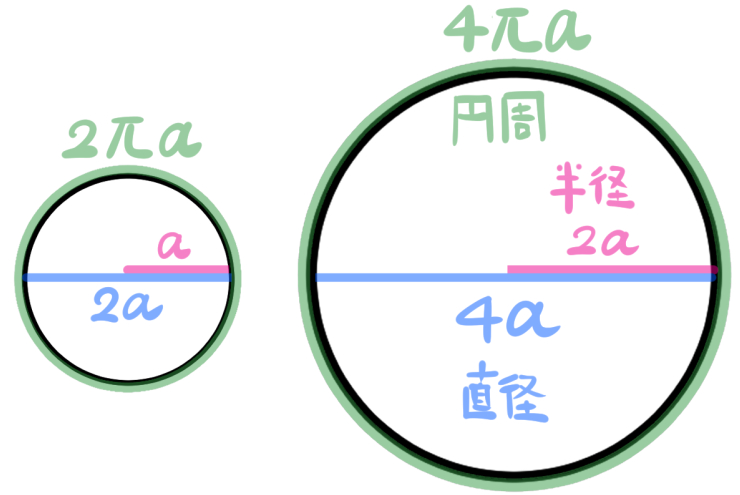
半径が不明なので、直径も不明となり、円周も不明となります。
半径をaと表すと、直径はその2倍の2aとなり、さらにπをかけた2πaが円周になります。





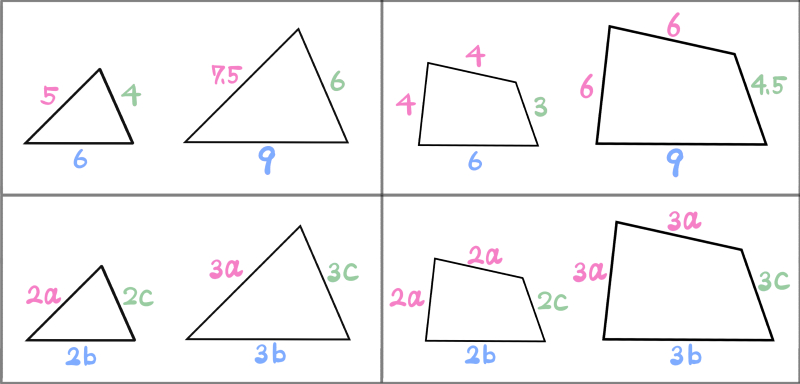

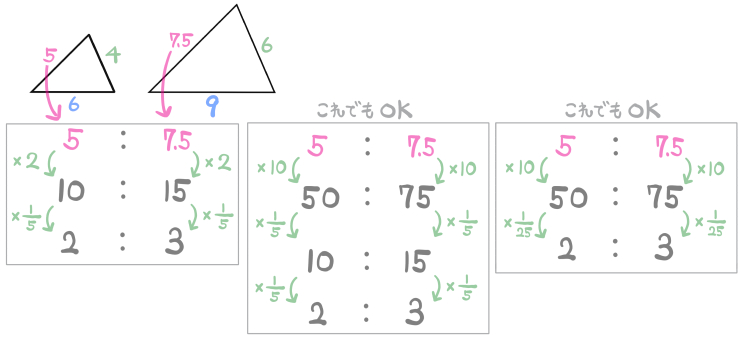
三角形の赤色の部分の辺の長さは「5:7.5」ですね。
このような小数の比を簡単にする手順はこうなります。
また辺の長さが「2a、3a」など、文字で表してある図形は、こう見るといいでしょう。
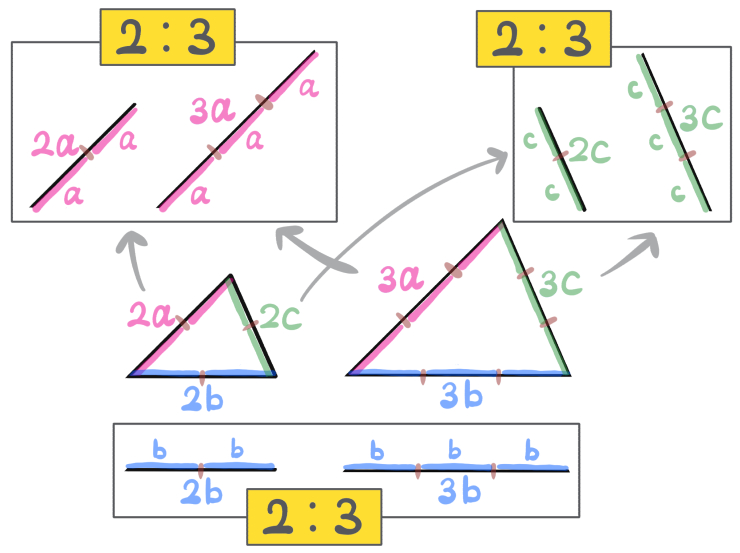
このように「基準となる長さa、b、cがあり、その長さが何個分あるかを表した図」だと思うとわかりやすいと思います。
円の相似比
それでは円の相似比について、同じように見ていきましょう。

半径が2の円と半径が3の円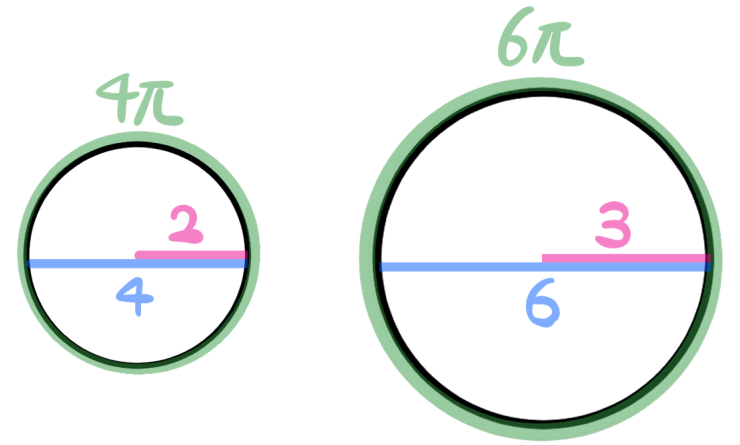
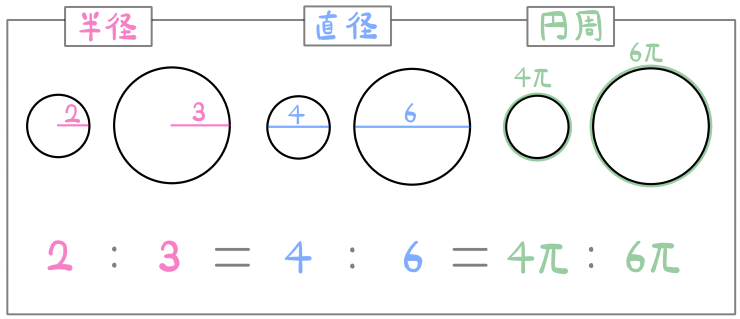
半径も直径も円周もすべて2:3になります。

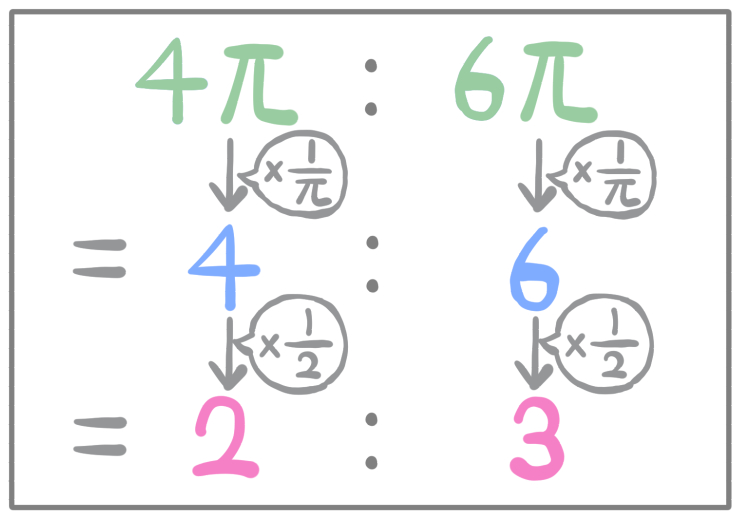
このように、対応する部分の長さを比べることができれば、相似比(相似な図形同士の大きさの比率)がわかるというワケです。
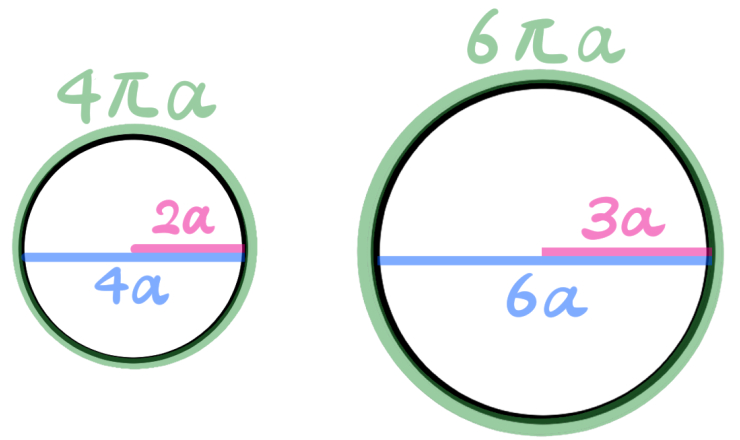
円の半径をそれぞれ2aと3aとおくことで、半径の比が2:3である二つの円になっています。
直径は半径の2倍なので、それぞれ4aと6aになり
円周は直径に円周率をかけた値なので、それぞれ4πaと6πaになります。

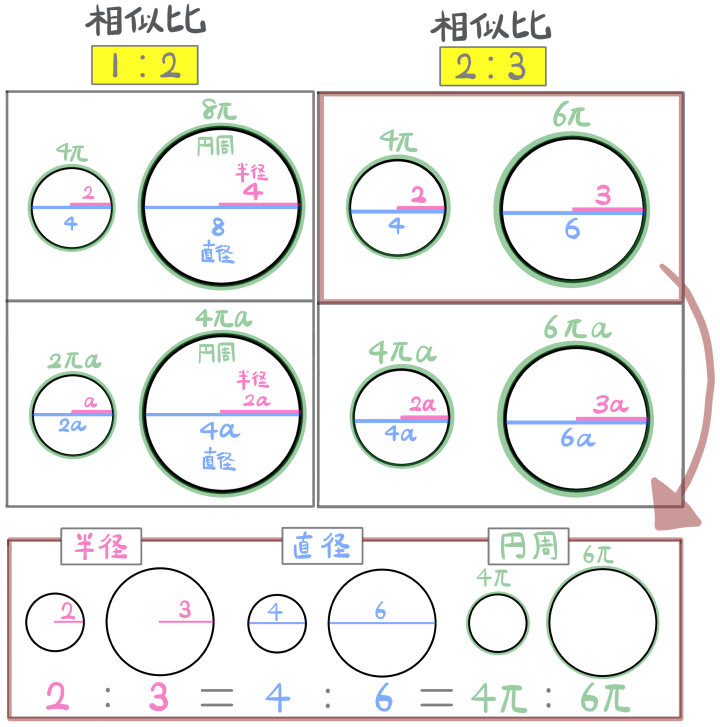
相似比とは何かについてのまとめ(平面図形)

相似比とは、形が同じ図形同士の大きさの比を表したものです。





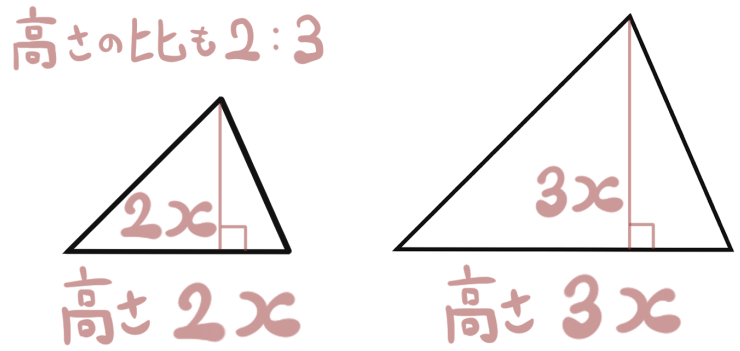
この相似な三角形は、高さの比が2:3なので、相似比も2:3ですね。(ただし、2つの図形が相似だとわかっていないと使えません)



円周の長さが2:3なので、相似比も2:3になります。(円と円はそもそも相似になっているので、相似であるかどうかの確認は必要ありません)

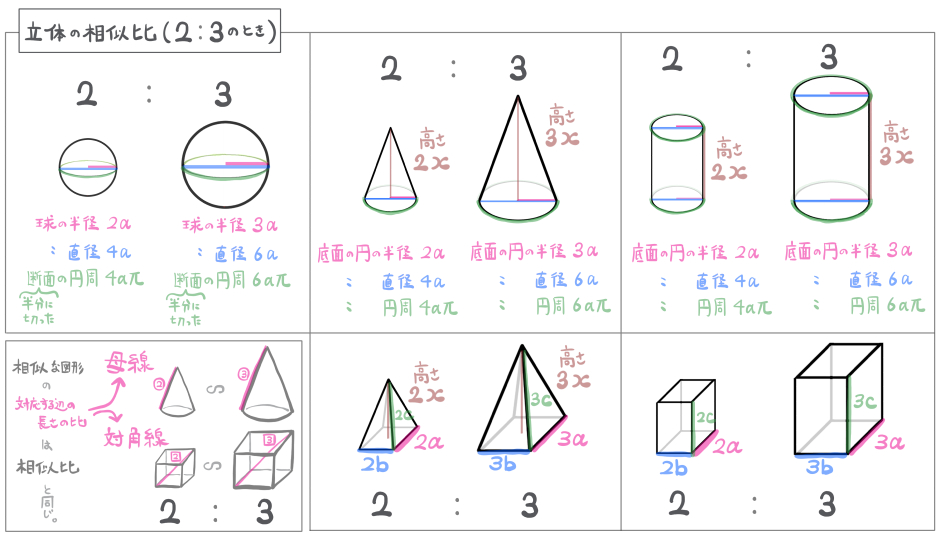
立体の相似比一覧|円錐や球、立方体など
立体の相似比も、相似な立体同士の大きさの比率を答えればよいです。
そしてその比率は、平面図形の場合と同じように、対応する部分の辺の長さの比を見ることでわかります。



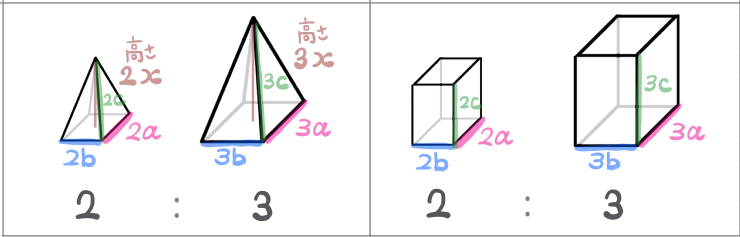
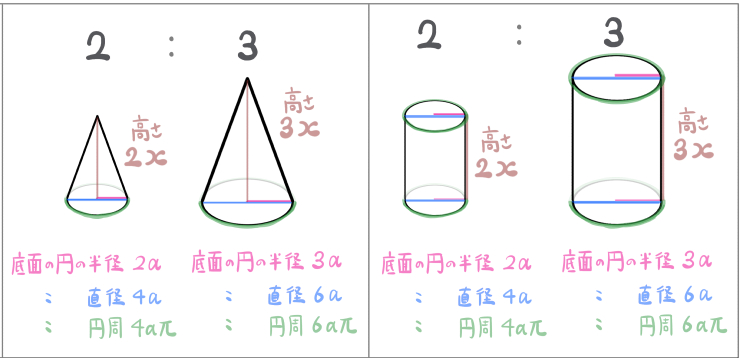
相似な円錐と相似な円柱
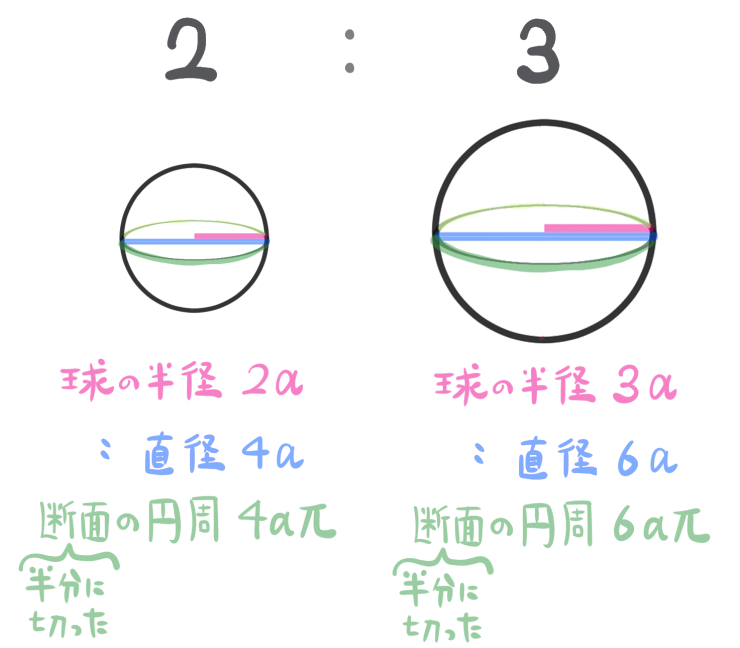
相似な球
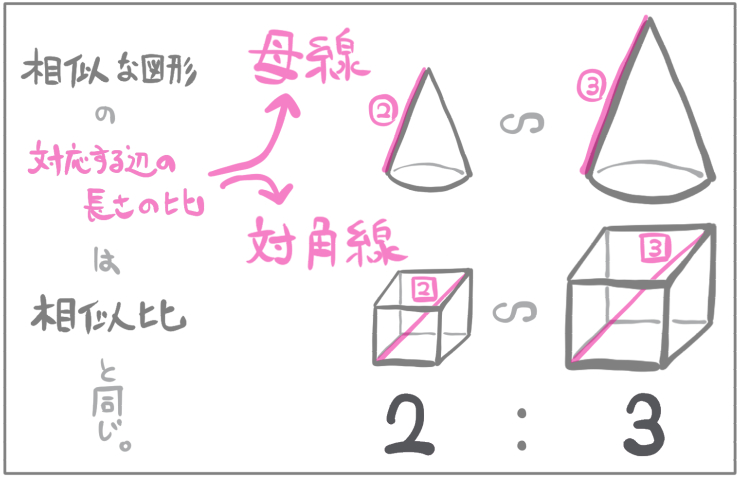
平面図形であろうと立体図形であろうと、相似な図形同士の、対応する部分の辺であれば、その長さの比が相似比になります。




相似比だと勘違いしやすい2辺の比との違い|両方使えると便利


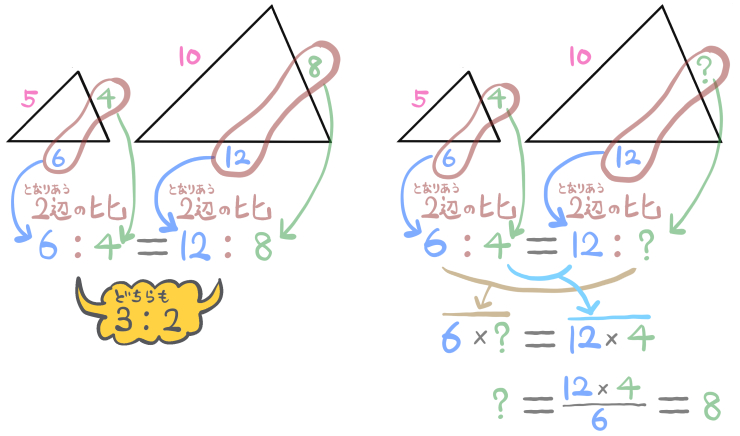
次の相似な三角形について?を求めよ。(それぞれの値は辺の長さを表すものとする)
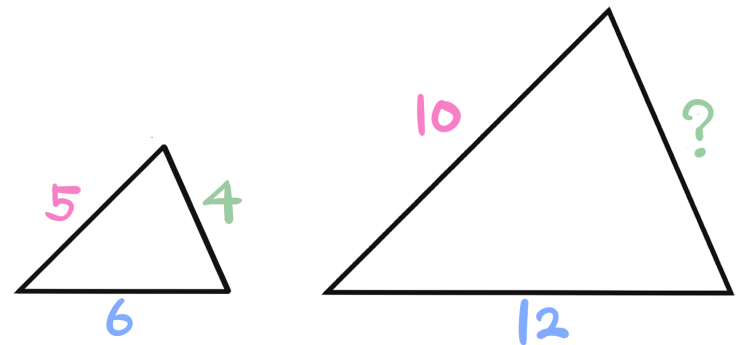

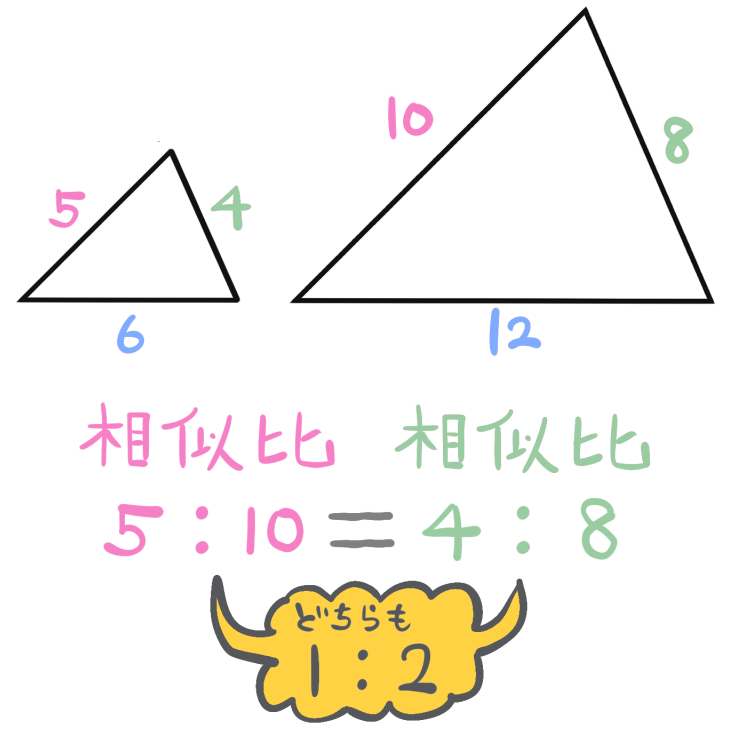


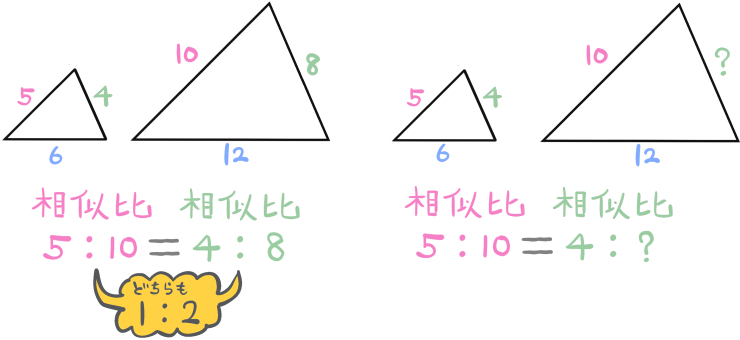

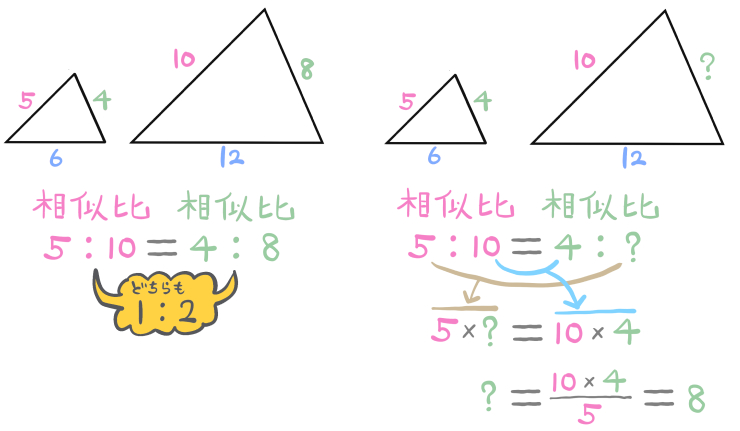

今度は相似比ではなく、三角形のとなり合う2辺の比を利用して解いてみます。
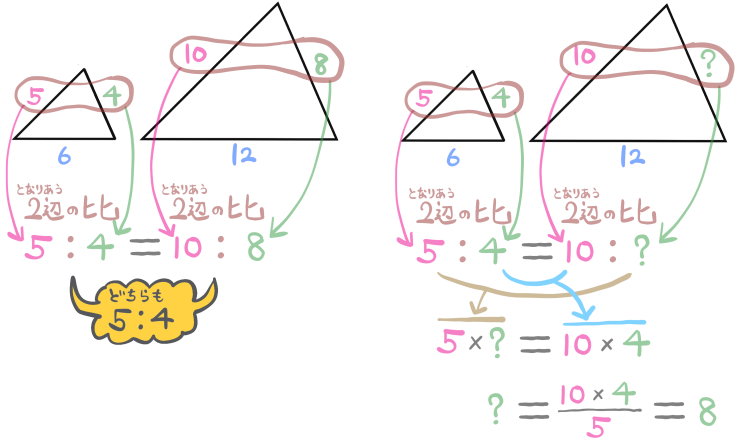
赤色と緑色の辺の長さの比は、この三角形の場合は5:4になっています。
「相似な図形のとなり合う2辺の比はそれぞれ等しい」という性質を使いました。
これを利用して、比例式を作ったということです。
ただしこの方法には注意点が2つあります。
2:選ぶ2辺によって、となり合う2辺の比は変わります。


赤色と緑色の辺の長さの比が5:4だったのに対して
青色と緑色の辺の長さの比は3:2になっていますね。
この方法を使う場合、相似比を使って解いているわけではない、ということは理解しておきましょう。
(実は、中学数学で最後のほうに学習する「三平方の定理」でも、「三角形の3辺の割合」が登場します。)
今みたいな問題を解くときに、「相似比」と、「3辺の割合(となり合う2辺の比)」を両方使えると、(大きな値でない限り)かなり暗算で解くことができます。
その方法はまた別のところで解説します。(限られた試験時間に少しでも余裕を作りたい方は習得していってください。)





























2つの三角形を見比べてみると、左と比べて右が2倍の大きさになっています。
それぞれの辺の長さがすべて2倍になっていますね。
こんなとき、△ABCと△DEFの相似比は1:2であると言えます。
ただし、それぞれの辺の長さは、これだけでは不明です。
左の三角形では長さがaの辺は、右の三角形では長さが2a(つまりaの2倍の長さ)になっています。
b、cも同じように、それぞれ2倍ずつの長さである2b、2cになっていることがわかります。
左と右で、相似な図形の大きさの比率が1:2になってるので、相似比は1:2になります。