

坂田先生
このページでは、中3数学で学習する相似な図形についての基本事項を1からていねいに説明します。

にゃんこ
ちなみに相似(そうじ)と読みます。
このページの内容
- 相似とはどのような関係か?わかりやすく解説
- 相似な図形と合同な図形の違いとは?
- 向きが違う相似な図形|頂点の順番や向きの揃え方
相似とはどのような関係か?わかりやすく解説

坂田先生
相似とはどのような関係かについて、一言でわかりやすく説明するならズバリこう言います。
形が同じで大きさが違う2つの図形のことを相似な図形と言うんだよ。

にゃんこ
例えば、次のような2つの図形がそうです。
四角形の場合
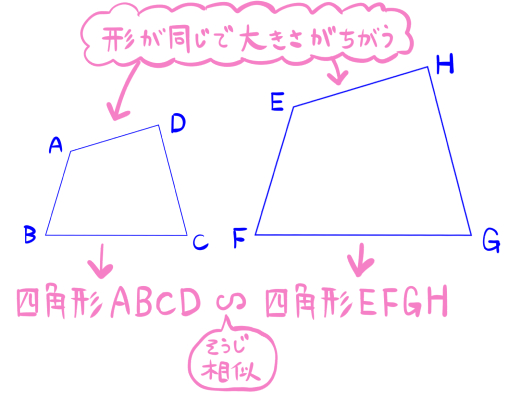
このような場合、「四角形ABCDと四角形EFGHは相似である」と言うことができます。
また、相似の記号∽を使ってこのように表現しても同じ意味になります。
四角形ABCD∽四角形EFGH
読み方:四角形ABCDそうじ四角形EFGH、と読みます。

坂田先生
ついでに、三角形の場合も見てみましょう。この例を見てください。
三角形の場合
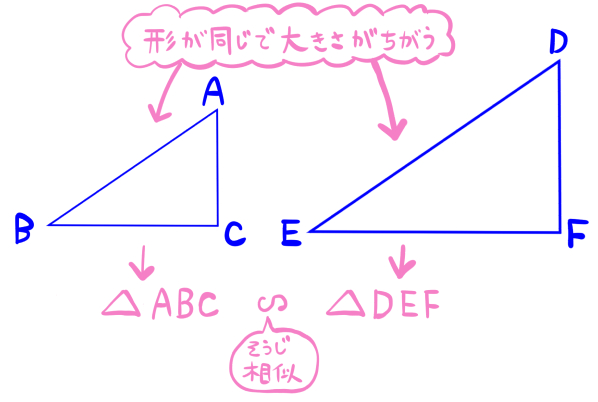
この2つの三角形は相似になっています。
このような場合、「△ABCと△DEFは相似である」と言えます。
相似の記号∽を使って同じ意味を表現すると、こうなります。
△ABC∽△DEF
読み方:三角形ABCそうじ三角形DEF
相似な図形と合同な図形の違いとは?

坂田先生
中2で学習した「合同な図形」は、形も大きさも同じである図形がテーマでした。

にゃんこ
それに対して「相似な図形」は、形だけが同じで大きさが違います。
つまり
「合同な図形」と「相似な図形」に共通しているのは、
「2つの図形の形が同じ」だということで、さらに
大きさまで同じなら「合同な図形」となり
大きさだけ違うなら「相似な図形」となります。

坂田先生
これまでに中学数学で学習した「2つの三角形の関係を説明する記号」をまとめると、こうなります。
相似、合同、面積の記号まとめ
- △ABC∽△DEF(△ABCと△DEFは相似である)
形だけ同じで大きさが違う。 - △ABC≡△DEF(△ABCと△DEFは合同である)
形も大きさも同じ。 - △ABC=△DEF(△ABCと△DEFの面積は同じである)
面積が同じ。
(相似なのか合同なのか、どちらでもないのかこれだけでは不明)
向きが違う相似な図形|頂点の順番や向きの揃え方

坂田先生
相似な図形を答える際には、「対応する頂点の並びに合わせて書くべし」というルールがあります。
これは、合同な図形でも同じことだったので、すでに理解している方は次の授業に進んでください。

にゃんこ
対応する頂点の並びに合わせて?なんのこっちゃ?
‥という方は、ていねいに説明しますので、このまま読み進めてください。
具体例で説明します

坂田先生
先程の相似な図形の説明では、同じ向きに並んでいる2つの図形を例にあげました。


坂田先生
では、2つの図形の向きが違っていたり、一方だけひっくり返されたような裏返しの図形である場合、どうすればいいでしょうか。

にゃんこ
例えばこんな場合です。
裏返しの図形の問題
次の2つの図形は相似である。このことを記号を使って表しなさい。
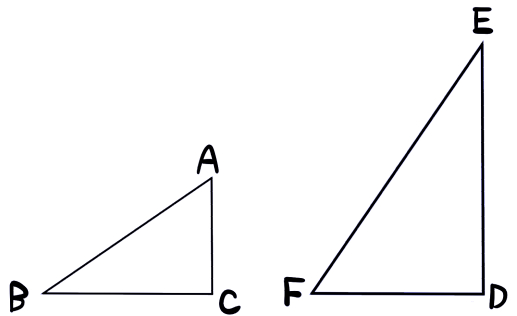

考え方:並びを合わせて対応する頂点を探す

にゃんこ
まず、右側の図形を、くるっと回してみます。
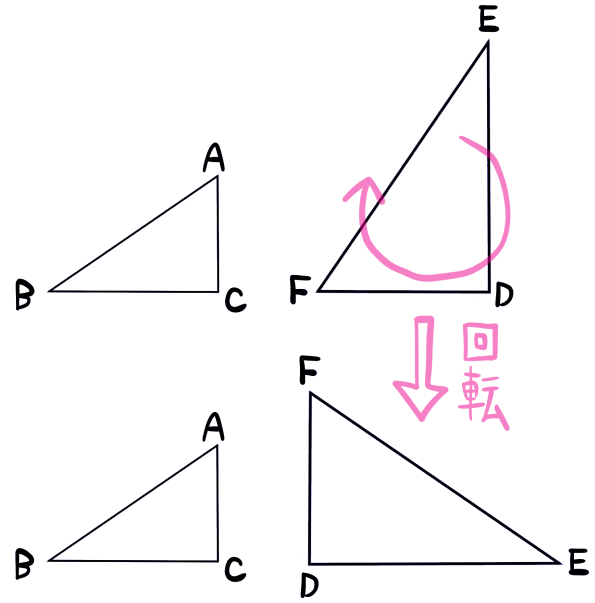

坂田先生
さらに向きをそろえてみます。
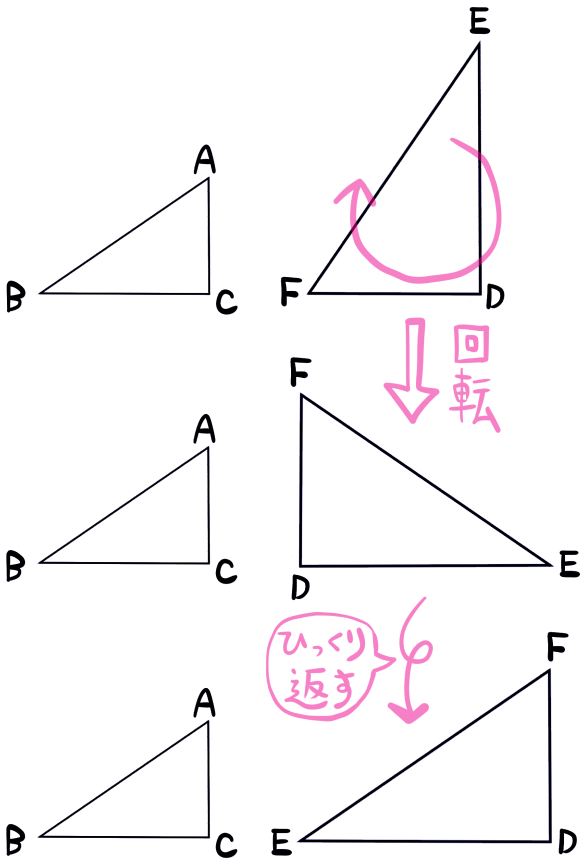

にゃんこ
すると‥
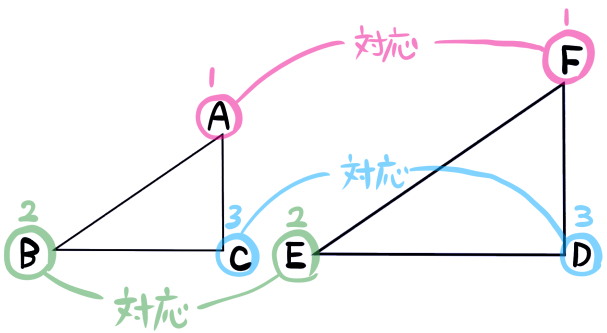
頂点Aと頂点Fが対応している(同じ位置にある)
頂点Bと頂点Eが対応している(同じ位置にある)
頂点Cと頂点Dが対応している(同じ位置にある)

坂田先生
ということに気が付きます。
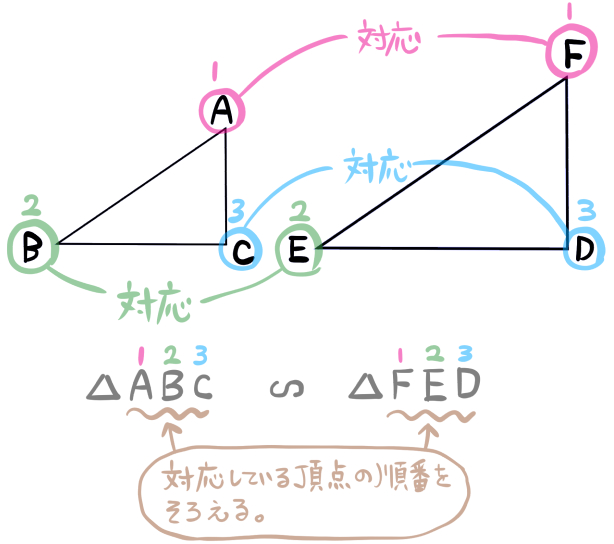
このとき「対応する頂点の順番をそろえて答える」ということが大事です。
よって△ABC∽△FEDが正解ということです。
ちなみに△ABC∽△DEFでは頂点が対応していないので不正解です。
このように、相似な図形を答える際には、「対応する頂点の並びに合わせて書くべし」というルールに注意しましょう。

にゃんこ
図形で「対応する」という言葉が出たら、こういう意味だと思ってください。
相似とはどのような関係かについてのおさらい&このページの復習

にゃんこ
このページの復習です。
・相似な図形とは、形が同じで大きさが違う図形のことを指します。
・合同な図形とは、形も大きさも同じ(つまり、ぴったり重ねることができる)図形のことを指します。
相似な図形の向きが同じ場合

相似な図形の向きが違う場合


相似、合同、面積の記号まとめ
- △ABC∽△DEF(△ABCと△DEFは相似である)
形だけ同じで大きさが違う。 - △ABC≡△DEF(△ABCと△DEFは合同である)
形も大きさも同じ。 - △ABC=△DEF(△ABCと△DEFの面積は同じである)
面積が同じ。
(相似なのか合同なのか、どちらでもないのかこれだけでは不明)




























