



中1中2の『式の値』難問20パターン|高校入試問題レベル
(1) \(\dfrac{1}{5}a=\dfrac{1}{2}b\)のとき、\(\dfrac{3a+10b}{2a+5b}\)の値を求めよ。(\(a\)、\(b\)は\(0\)でない)

(2) \(3x+y=x-2y\)のとき、\(\dfrac{5x-y}{3x+2y}\)の値を求めよ。(\(x\)、\(y\)は\(0\)でない)


(3) \(5a-2b=5\)のとき、\(\dfrac{3a-2b}{2}+\dfrac{2a-b}{3}+\dfrac{7}{6}a\)の値を求めよ。

(4) \(a^{2}b=4\)のとき、\(\left( 3ab^{2}\right) ^{3}\div \left( -3ab\right) ^{2}\times a^{7}\)の値を求めよ。

(5) \(\dfrac{1}{a}+\dfrac{1}{b}=3\)のとき、\(\dfrac{5a-ab+5b}{a+b}\)の値を求めよ。

(6) \(\dfrac{a+b}{2}=\dfrac{a-b}{3}\) \(( \neq 0) \) のとき、\(\dfrac{b}{a}\)の値を求めよ。

(7) \(\dfrac{1}{a}-\dfrac{1}{b}=1\)のとき、\(\dfrac{5ab}{a-b}\)の値を求めよ。

(8) \(\dfrac{x+3y}{xy}=\dfrac{2}{7}\)のとき、\(\dfrac{15}{x}+\dfrac{5}{y}\)の値を求めよ。

(9) \(2x+3y=5x-6y\)のとき、\(\dfrac{2x+3y}{x-y}\)の値を求めよ。(\(x\)、\(y\)は\(0\)でない)

(10) \(a:b=1:2\)のとき、\(\dfrac{\left( 2a+b\right) ^{2}}{3a^{2}+ab+b^{2}}\)の値を求めよ。

(11) \(a:b=2:3\) 、\(b:c=3:5\)のとき、\(\dfrac{c}{a}\)の値を求めよ。

(12) \(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\)のとき、\(\dfrac{ab+bc+ca}{a^{2}+b^{2}+c^{2}}\)の値を求めよ。(\(a\)、\(b\)、\(c\)は\(0\)でない)

(13) \(2a=3b\)のとき、\(\dfrac{\left( a-b\right) ^{2}}{\left( a+b\right) ^{2}}\)の値を求めよ。(\(a\)、\(b\)は\(0\)でない)

(14) \(a+b=8\) 、\(b+c=12\)、\(a+c=10\)のとき、\(a+b+c\)の値を求めよ。

(15) \(a+b+c=0\)のとき、\(\dfrac{c}{a+b}+\dfrac{a}{b+c}+\dfrac{b}{c+a}\)の値を求めよ。(\(a\)、\(b\)、\(c\)は\(0\)でない)

(16) \(ab=6\) 、\(bc=15\) 、\(ac=10\)のとき、\(abc\)の値と\(a\)の値を求めよ。(\(a\)、\(b\)、\(c\) は自然数とする)
 【解説の途中からややこしいと感じた方へ】abcを2乗した値が2×3×5の2乗の値(すなわち900)と等しいということは、abcの値は「2乗して900になる値」である \(30\) または \(-30\) ということになります。問題文にa、b、cは自然数という条件があるので、その3つを掛け合わせたabcは正の数ですね。なので、abcの値は \(-30\)はあり得ないので、 \(30\) のみとなります。
【解説の途中からややこしいと感じた方へ】abcを2乗した値が2×3×5の2乗の値(すなわち900)と等しいということは、abcの値は「2乗して900になる値」である \(30\) または \(-30\) ということになります。問題文にa、b、cは自然数という条件があるので、その3つを掛け合わせたabcは正の数ですね。なので、abcの値は \(-30\)はあり得ないので、 \(30\) のみとなります。(17) \(a+b+c=0\) 、\(\left( a+b\right) ^{2}b^{2}\left( b+c\right) ^{2}=25\)のとき、\(abc\)の値を求めよ。(\(a\)>\(0\)、\(b\)>\(0\)、\(c\)>\(0\)とする)

(18) \(a+b+c=3\) 、\({\small a\left( \dfrac{1}{b}+\dfrac{1}{c}\right) +b\left( \dfrac{1}{a}+\dfrac{1}{c}\right) +c\left( \dfrac{1}{a}+\dfrac{1}{b}\right) =1}\)のとき、\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)の値を求めよ。


(19) \(a+2b=3c\) 、\(2a+b=4c\)のとき、\(\dfrac{c}{a}\)の値を求めよ。( \(a\)、\(b\)、\(c\) は0でない)

(20) \(\dfrac{a+b}{2}=\dfrac{b+c}{3}=\dfrac{c+a}{4}\)のとき、\(\dfrac{a^{2}}{bc}\)の値を求めよ。( \(a\)、\(b\)、\(c\) は0でない)


※セット版も単品版もあります。










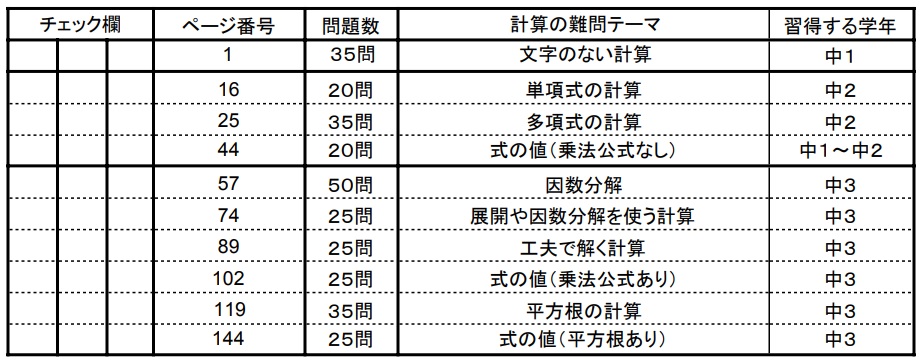
- 文字のない計算(正負の数の計算問題・四則演算)
- 単項式の計算(単項式の乗除)
- 多項式の計算問題の難問
- 式の値(乗法公式なし)(←このページ)
- 因数分解の難問
- 展開や因数分解を使う計算(多項式の計算)
- 工夫で解く計算問題
- 式の値(乗法公式あり)
- 平方根の計算問題の難問
- 式の値(平方根あり)




























