

にゃんこ
ここでは中学数学や高校入試対策として練習しておきたい三平方の定理を使う平面図形の難問について学習できます。
このページの内容
- 三平方の定理を使う平面図形の難問たち
- 三平方の定理を使う円や半円をからめた問題たち
三平方の定理を使う平面図形の難問たち
三平方の定理を利用して三角形の高さを求める問題
次の図のような三角形ABCがあり、BC⊥AHである。
このとき、AHの長さを求めよ。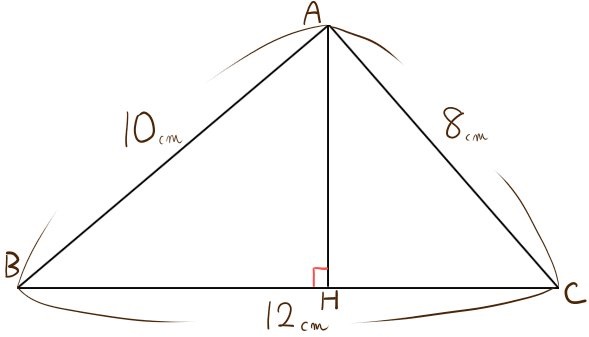
答え:\(\dfrac{5}{2}\sqrt{7}\)(㎝)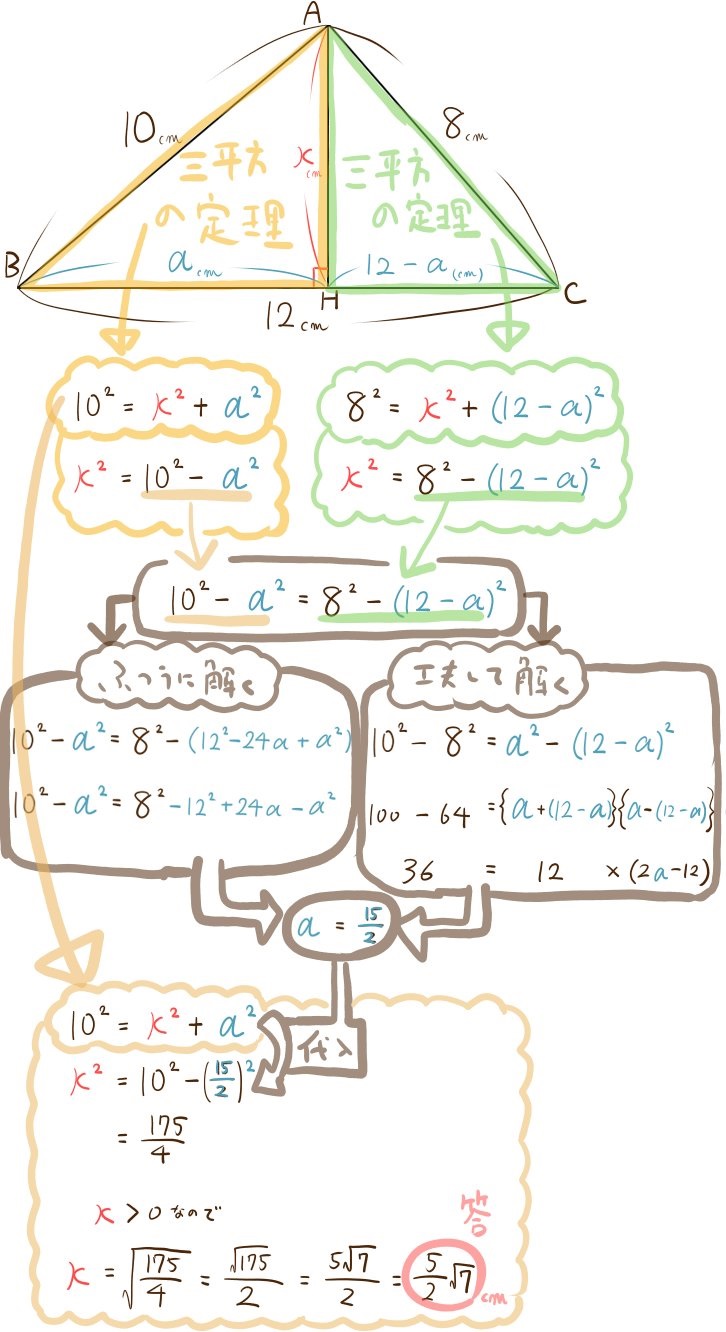

三平方の定理を使う、このパターンは頻出なので基本の型として慣れておきましょう。また、解説中に『ふつうに解く』と『工夫して解く』の2種類の解き方が登場していますので、確認しておいてください。
三平方の定理を利用して長方形の対角線を求める問題
この長方形の対角線の長さを求めよ。ただしこの長方形の面積は \(2\sqrt{3}\)(㎠)とする。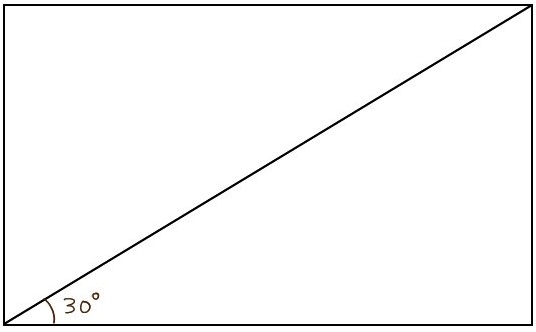
答え:\(2\sqrt{2}\) (㎝)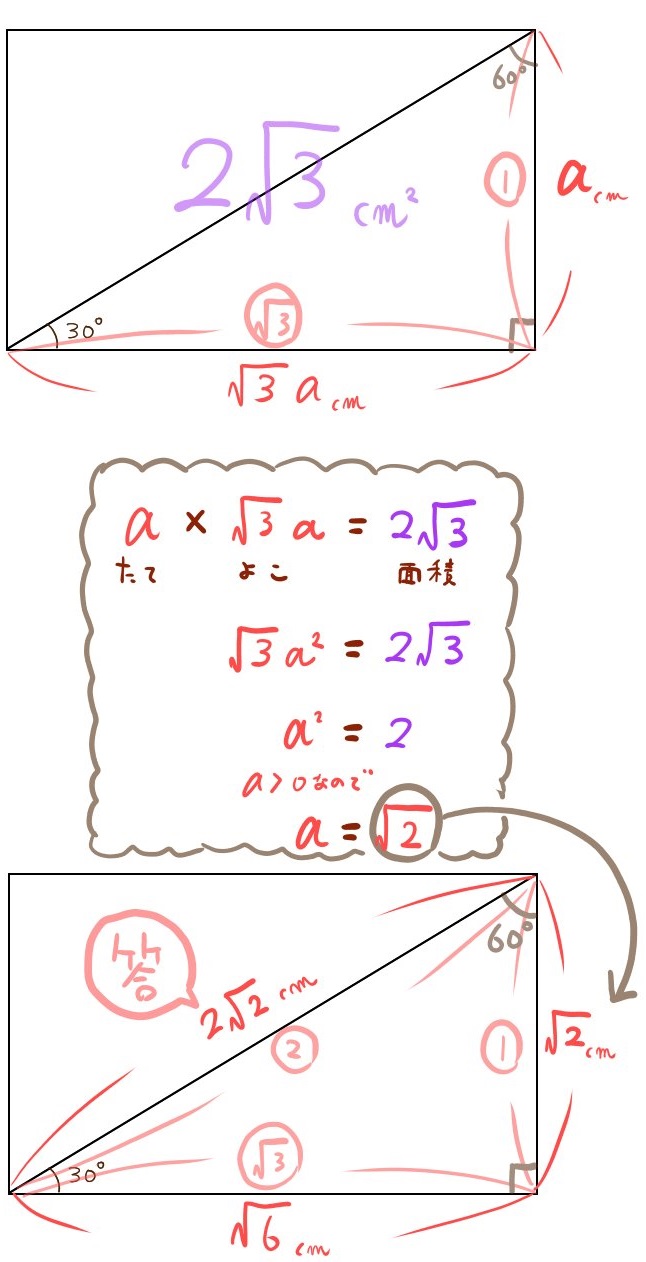

長方形の縦の長さと横の長さの比が1:\(\sqrt{3}\)になるので、縦をa(㎝)とすると横は\(\sqrt{3}a\) (㎝)とおくことができます。このように文字を使って比を表す方法を学びます。
辺の長さの比を使って解く問題
三角定規のかたちをした2種類の三角形を以下の図のように張り合わせ、多角形を作った。この多角形の周りの長さが36㎝であるとき、頂点Cと頂点Eを結んだ線分CEの長さを求めよ。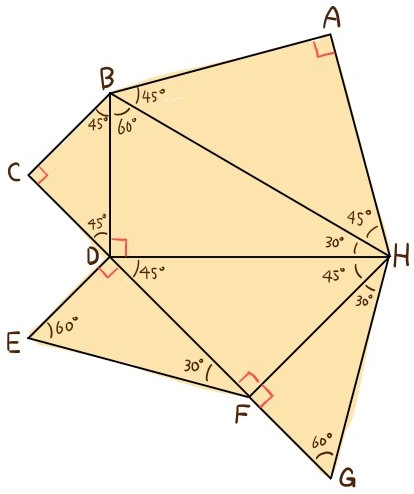
答え: \(3\sqrt{2}\) (㎝)CBの長さを \(x\) ㎝とすると、各辺の長さは次のようにおける。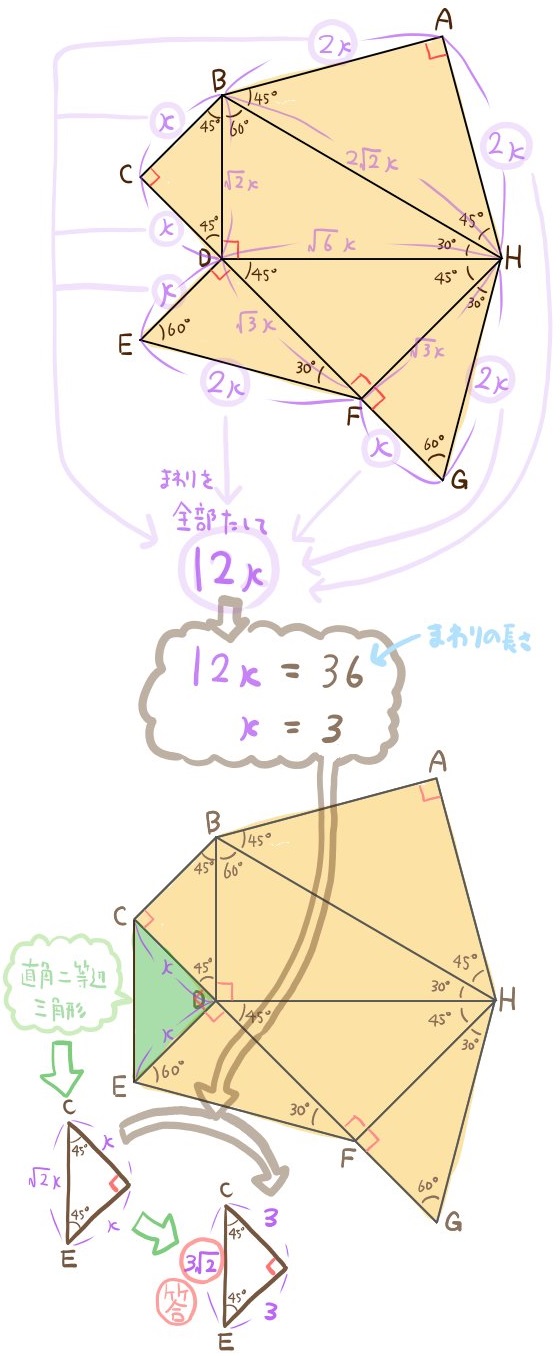

三角定規の2種類三角形の辺の比を利用して解く問題です。このような複雑さの問題が出ることは少ないのですが、各辺の比を文字式で書き加えてゆく力は、入試対策でも十分使う可能性があります。よって、その練習として用意しました。
三平方の定理を使う平面図形の応用問題
次の図のような三角形がある。
∠AEC=∠ADC=90°
AB=AC=5㎝
BC=6㎝である。(明訓高校)
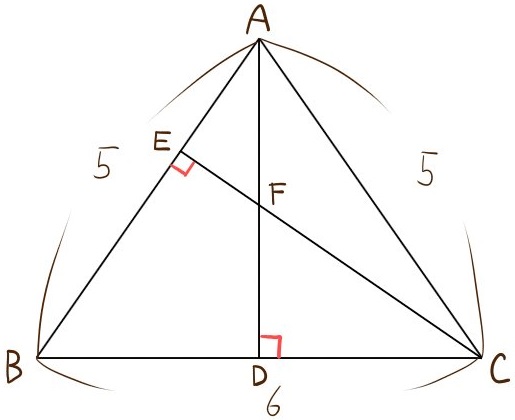
(1)△ABCの面積と、CEの長さを求めよ。
答え:△ABCの面積は12(㎠)、CEの長さは \(\dfrac{24}{5}\) (㎝)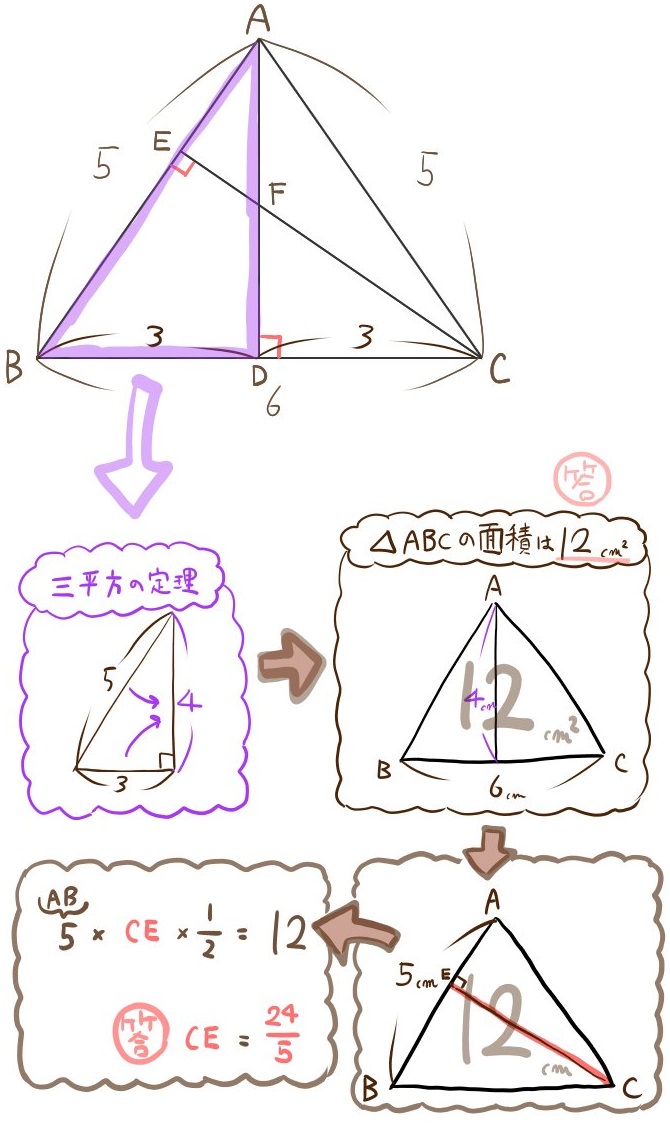

(2)△CFDの面積と△CBEの面積の比を最も簡単な整数の比で表せ。
答え:(△CFDと△CBEの面積比は)25:64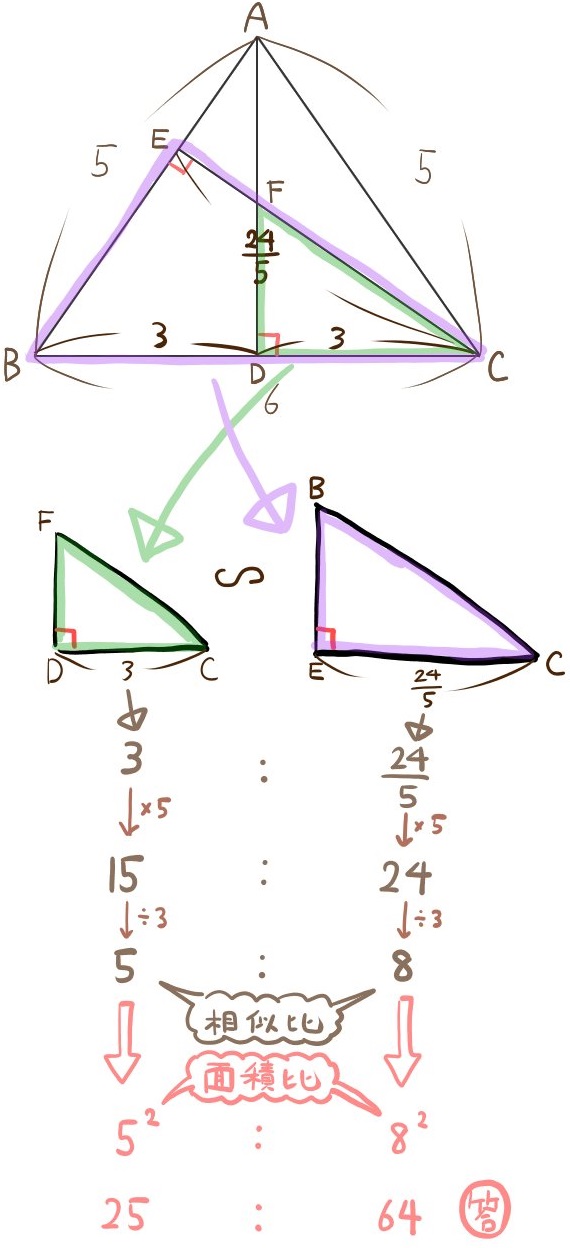

(3)△CFDの面積を求めよ。
答え: \(\dfrac{27}{8}\) (㎠)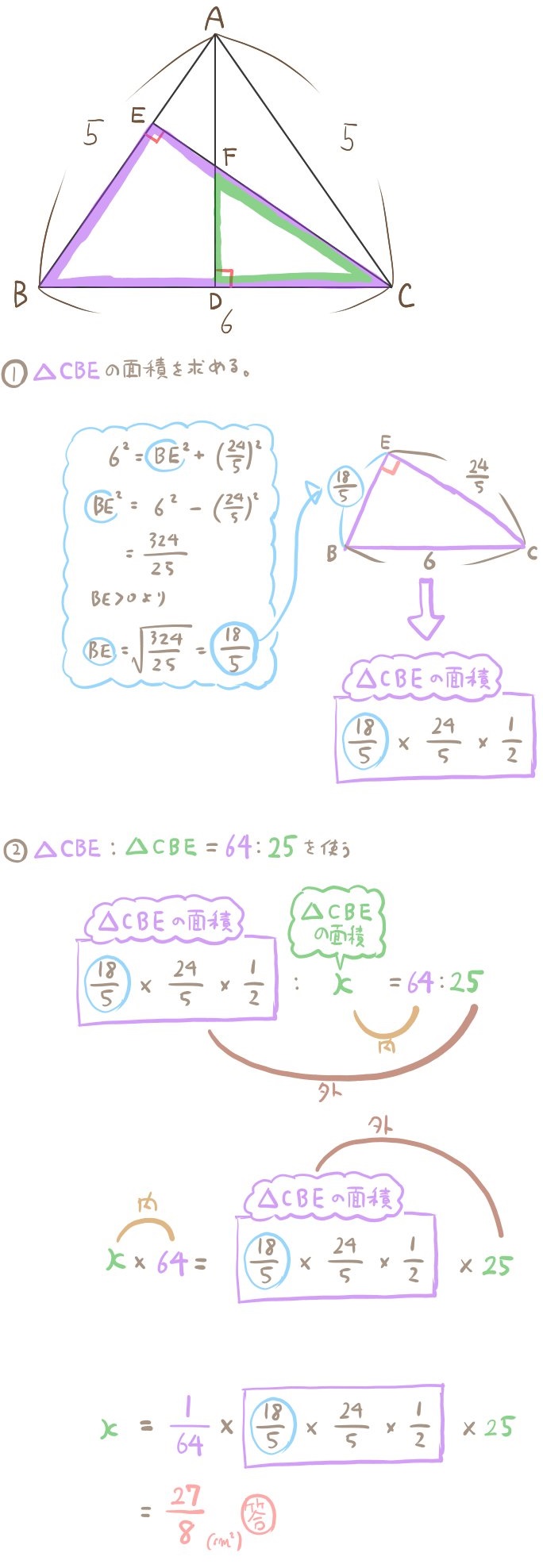

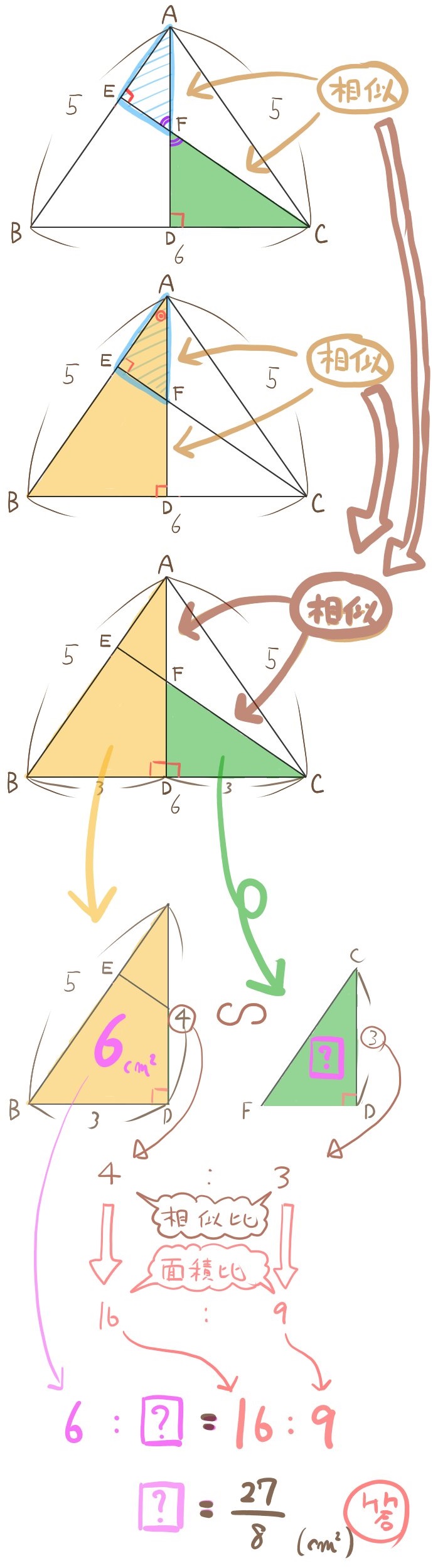
問題文の条件に2か所、90°がありました。直角三角形があるところは三平方の定理を使う可能性がありますので、その点を踏まえつつ解答にとりかかる癖をつけておきましょう。(3)は別解も含めて2パターンでスラスラ解ける状態に仕上げておきましょう。
三平方の定理で方程式を作る難問
下の図について考える。
AH:BH=3:4
∠BAC=∠AHC=90°
BC=6(㎝)である。
△ABCの面積を求めよ。
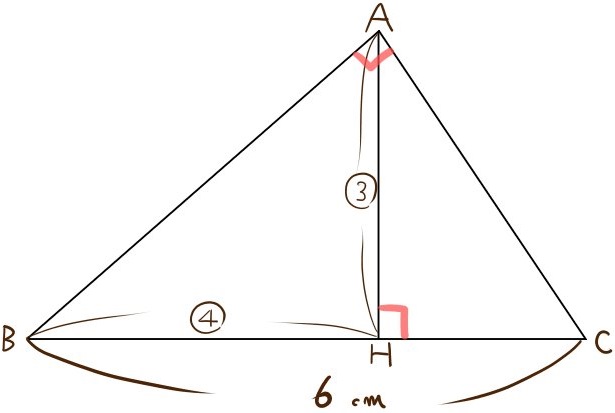
答え: \(\dfrac{216}{25}\) (㎠)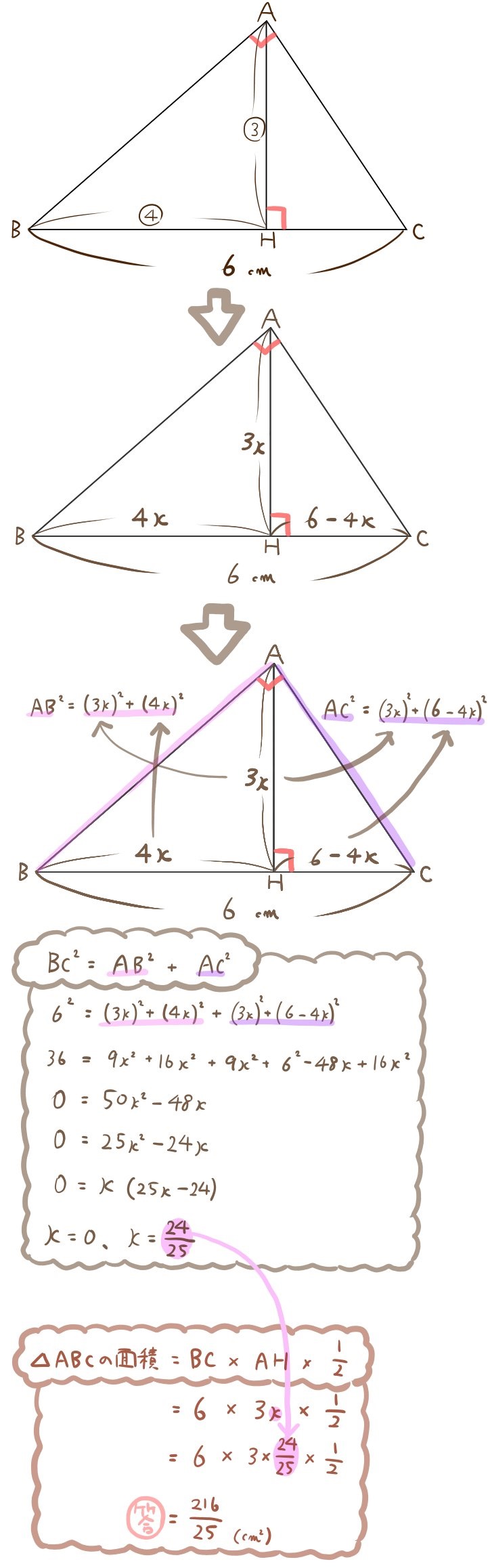

三平方の定理で方程式を作るパターンです。これもまた、辺の長さの比を文字で表しています。
平行四辺形と相似比と三平方の定理
次のような平行四辺形ABCDがある。
AB=AF
AB=15㎝
AD=25㎝
∠BAC=90°
BC⊥AE
であるとき、三角形AGHの面積を求めよ。(神奈川)
答え: \(\dfrac{25}{4}\) (㎠)
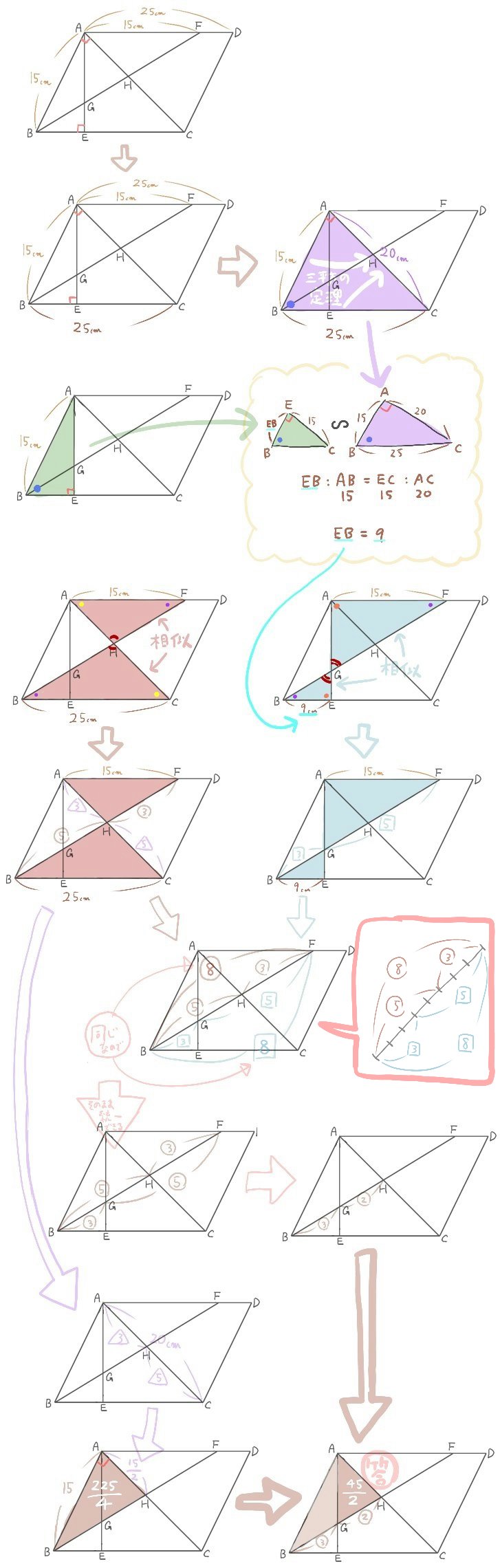

ここでは2通りに表した辺の比を統一するテクニックが登場しています。知らないと戸惑う事柄ですので、解説だけでも一読しておきましょう。
三平方の定理を使う円や半円をからめた問題たち

にゃんこ
後半は、三平方の定理と円や半円をからめた問題について練習したい方のためのページになります。
学習ページはこちら:円や半円の難問たち

坂田先生
このような問題たちを学習できます。
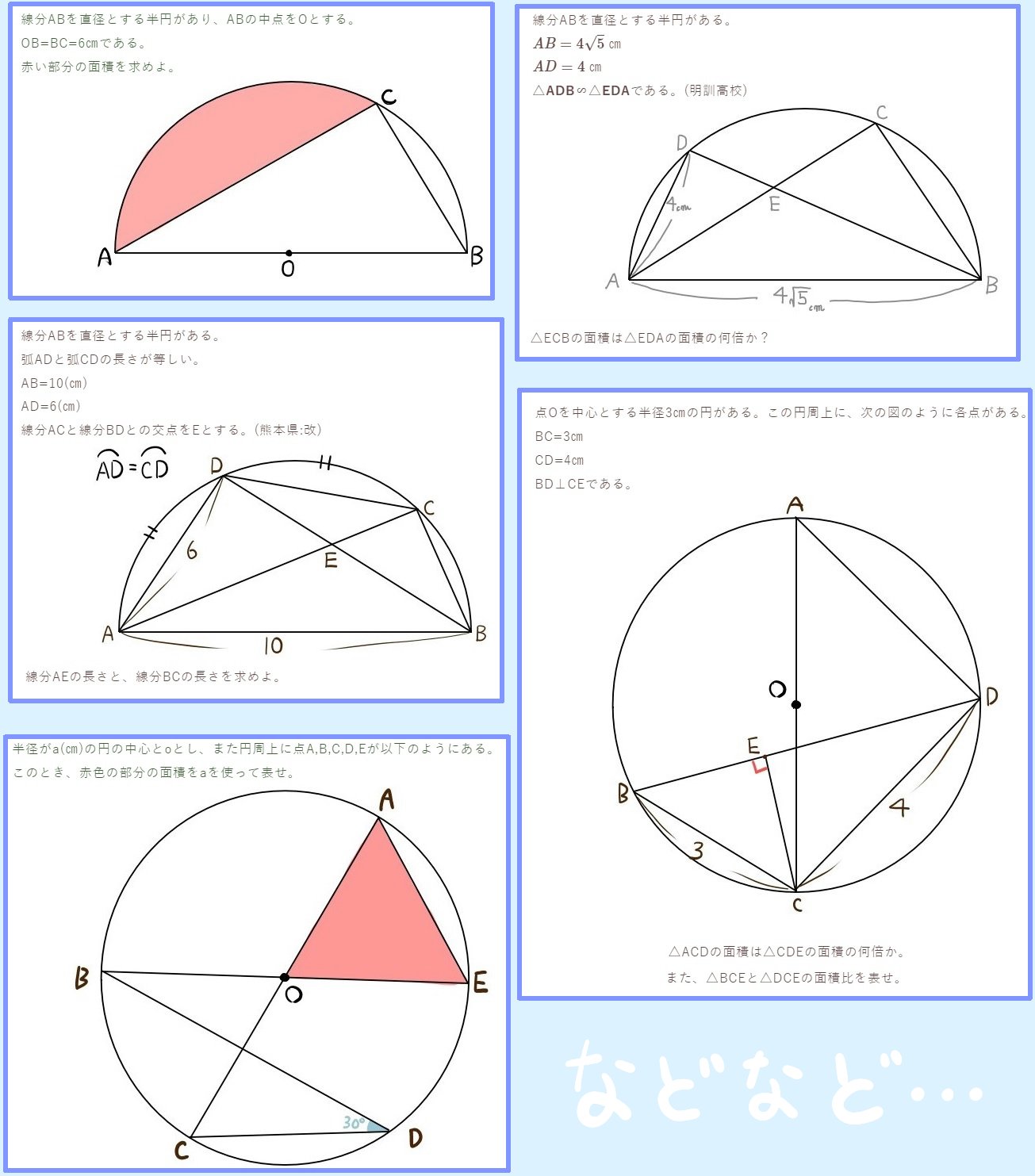

にゃんこ
高校入試対策の問題としてまとめましたので、三平方の定理だけでなく、相似比や面積比など、様々な学習事項を駆使して解く応用問題となっています。
円の問題にて三平方の定理が登場する典型的なパターン






























円が登場する場面では、直径が登場するとそこに直角三角形ができ、三平方の定理を利用するという場面が頻繁にあります。
また、円の半径は等しいので、二等辺三角形や正三角形なども可能性として考えられ、これもまた、三平方の定理を利用することにつながる場合があります。