



工夫して解く計算問題の難問|中学3年~高校入試問題レベル
(1) \(1111^{2}\times 3^{2}-3330\times 3336\)

(2) \(146\times 148-151\times 302+1501+150^{2}\)

(3) \({\small 211^{2}-335^{2}-189^{2}-243^{2}+365^{2}+257^{2}}\)

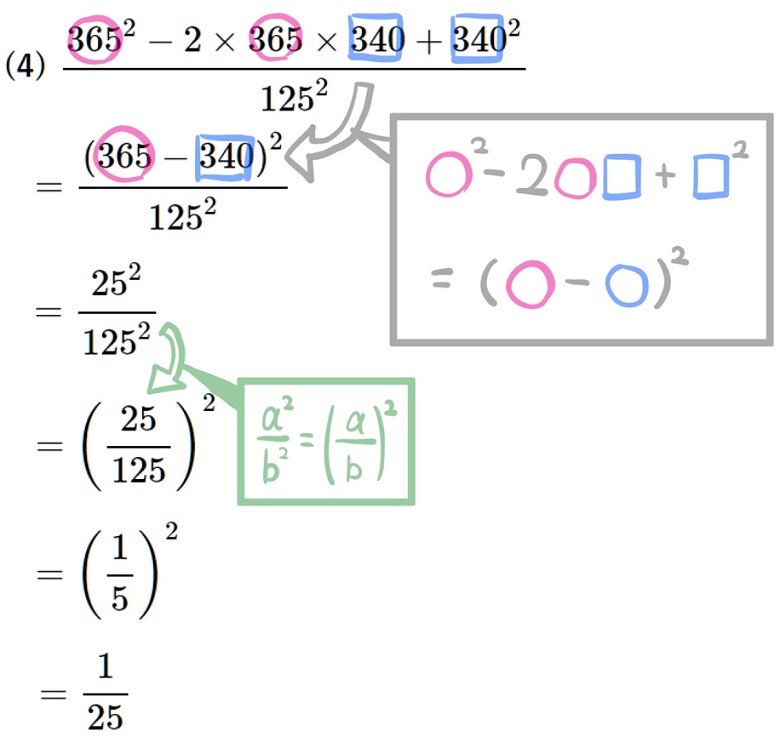
(4) \(\dfrac{365^{2}-2\times 365\times 340+ 340^{2}}{125^{2}}\)
(5) \(\dfrac{121^{2}-12100}{33}\)

(6) \(\dfrac{169-121}{169-22\times 13+121}\)

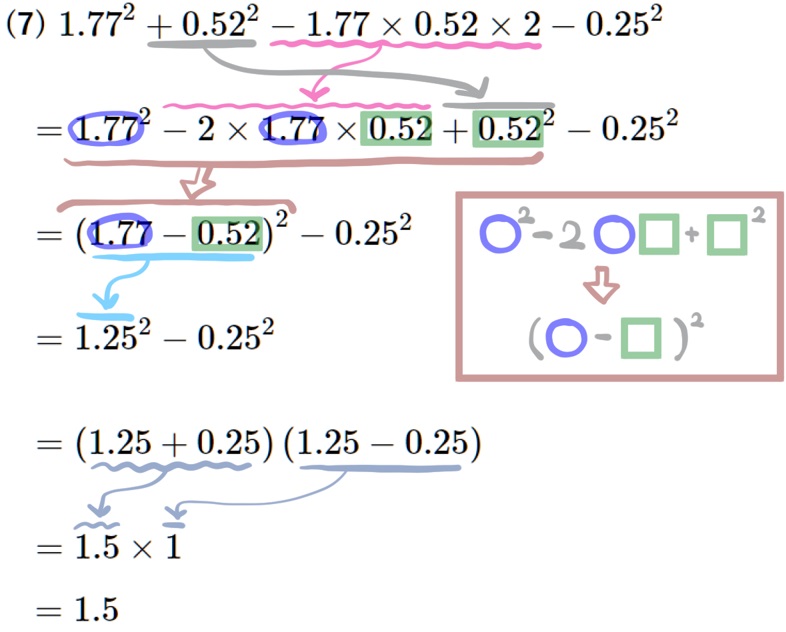
(7) \(1.77^{2}+0.52^{2}-1.77\times 0.52\times 2-0.25^{2}\)
(8) \(\dfrac{1234^{2}+2469}{1235}\)
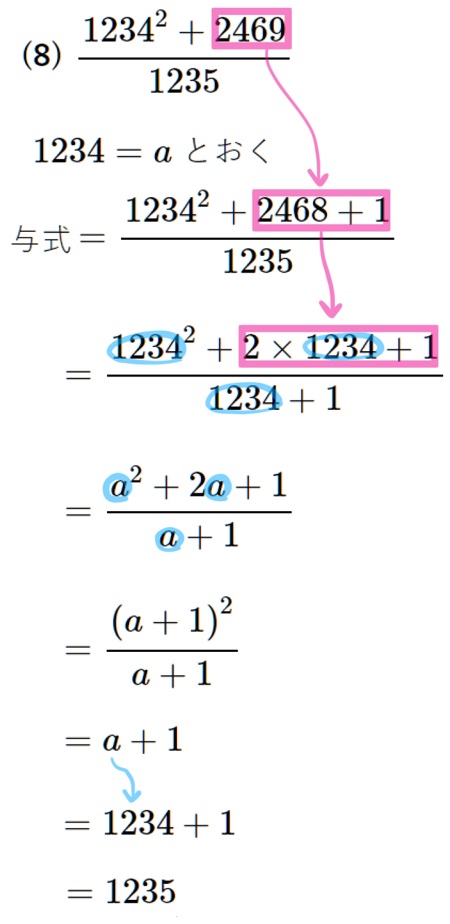
(9) ![]()

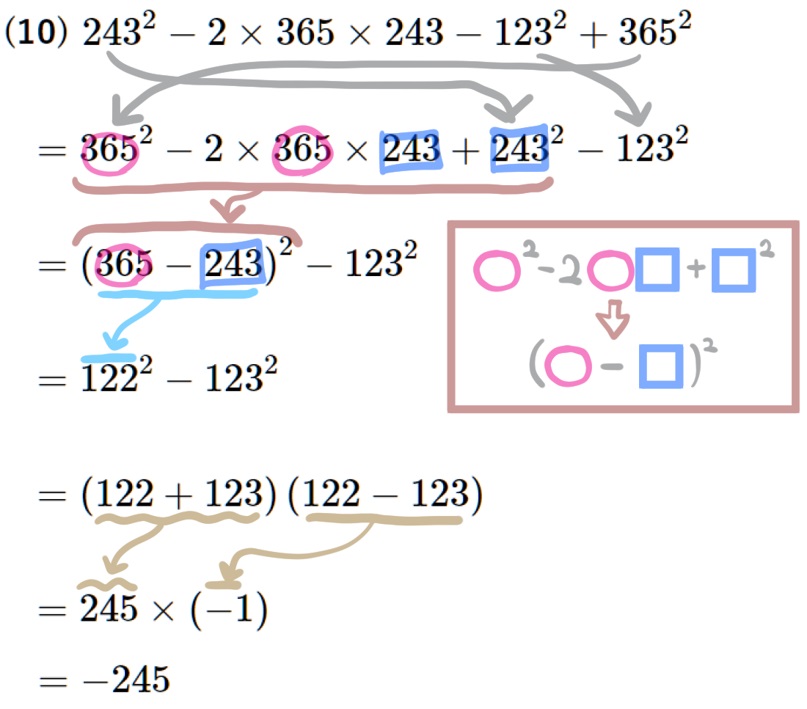
(10) \(243^{2}-2\times 365\times 243-123^{2}+365^{2}\)
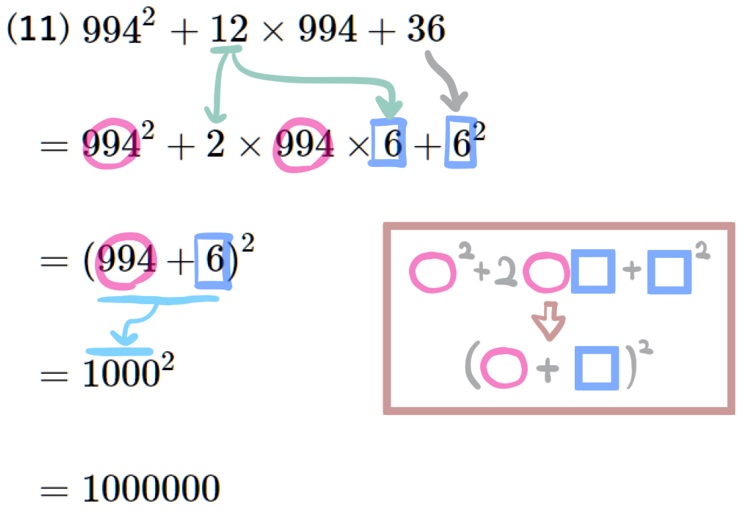
(11) \(994^{2}+12\times 994+36\)
(12) \(1.72^{2}+4\times 1.72\times 0.14+4\times 0.14^{2}\)

(13) \(\dfrac{222-33}{111\times 444-11\times 99}\)

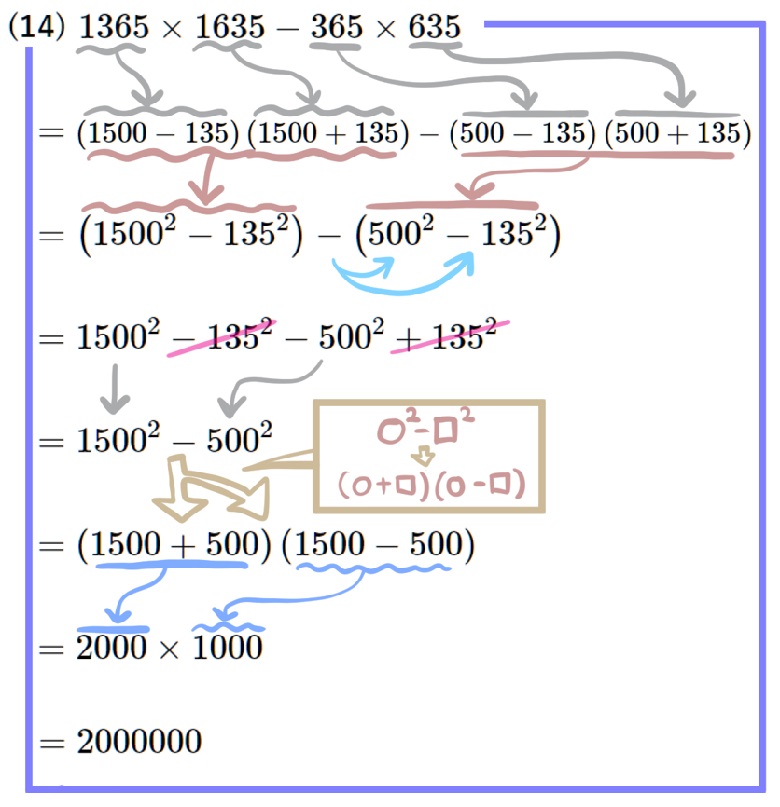
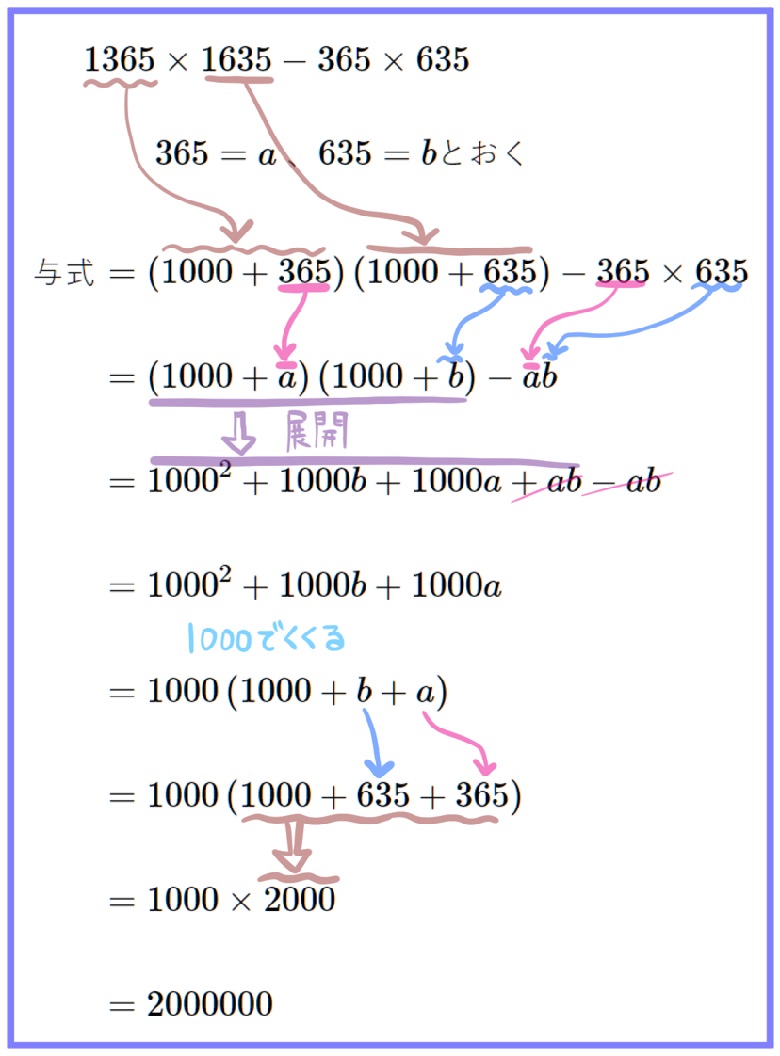
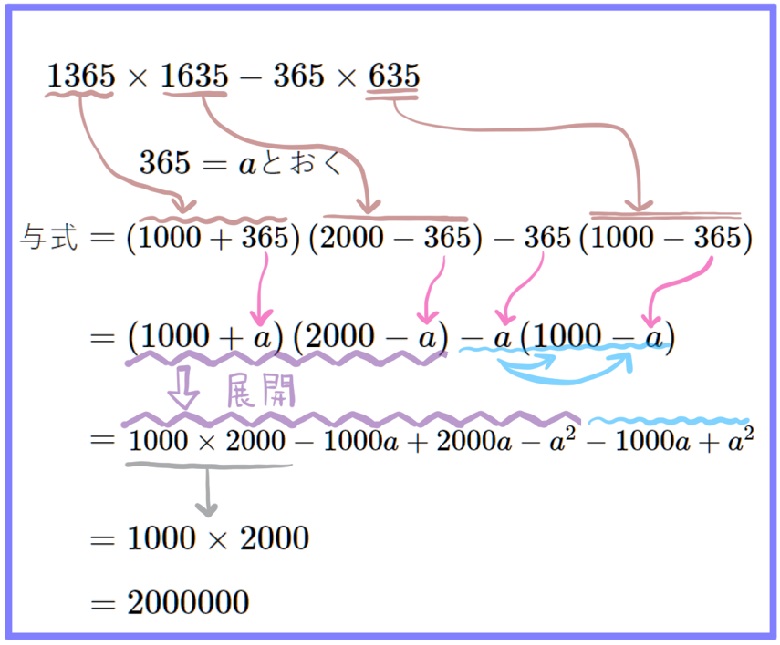
(14) \(1365\times 1635-365\times 635\)
(15) \(\dfrac{12345^{3}-2\times 24690}{12343\times 12347}\)

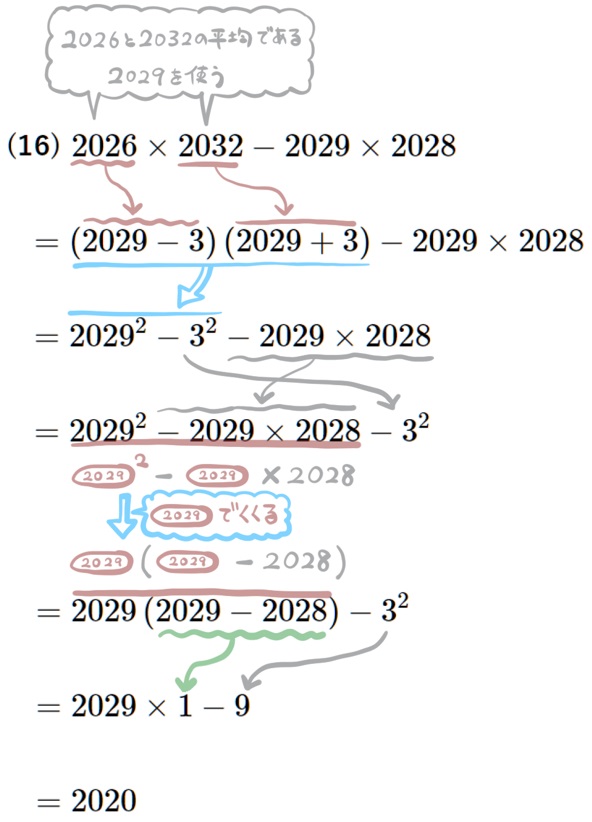
(16) \(2026\times 2032-2029\times 2028\)
(17) \(328\times 1433-322\times 1439\)

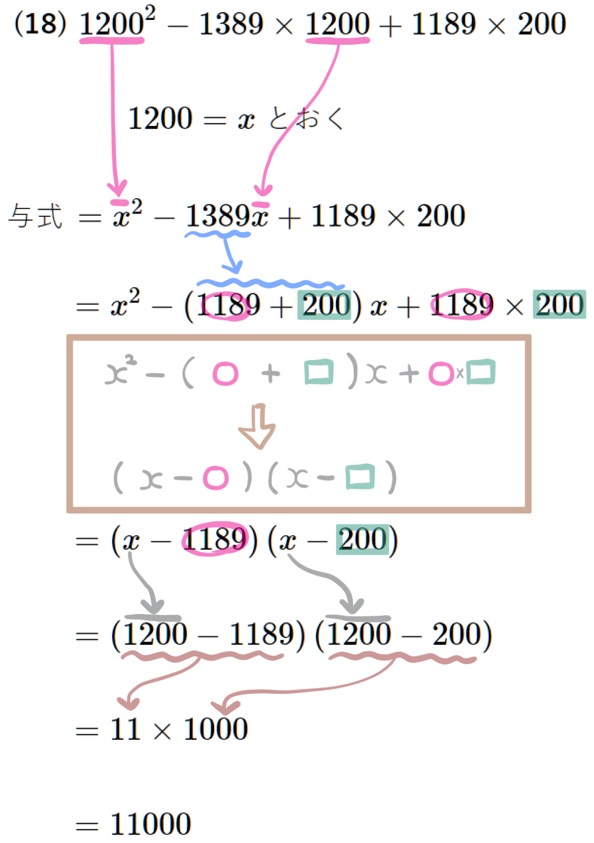
(18) \(1200^{2}-1389\times 1200+1189\times 200\)
(19) \({\small 12.34\times 45.67+54.33\times 11.11+1.23\times 54.33}\)

(20) \(5035\times 5031-4970\times 4964-5\)

(21)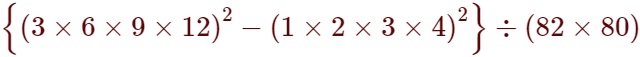

(22) 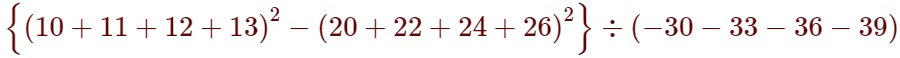
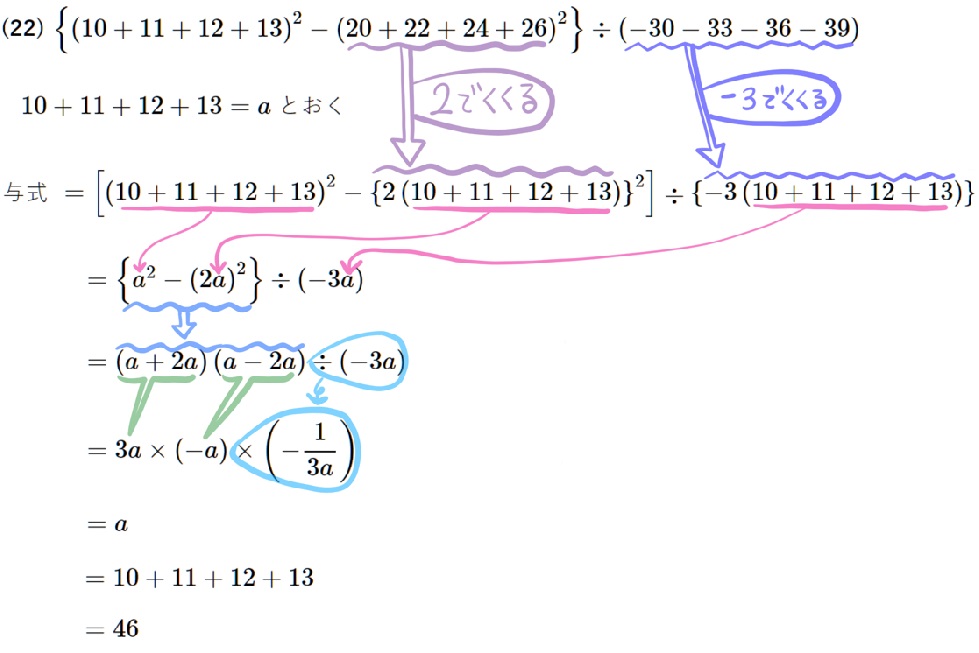
(23) \(\dfrac{22^{3}-11^{3}}{77}\)
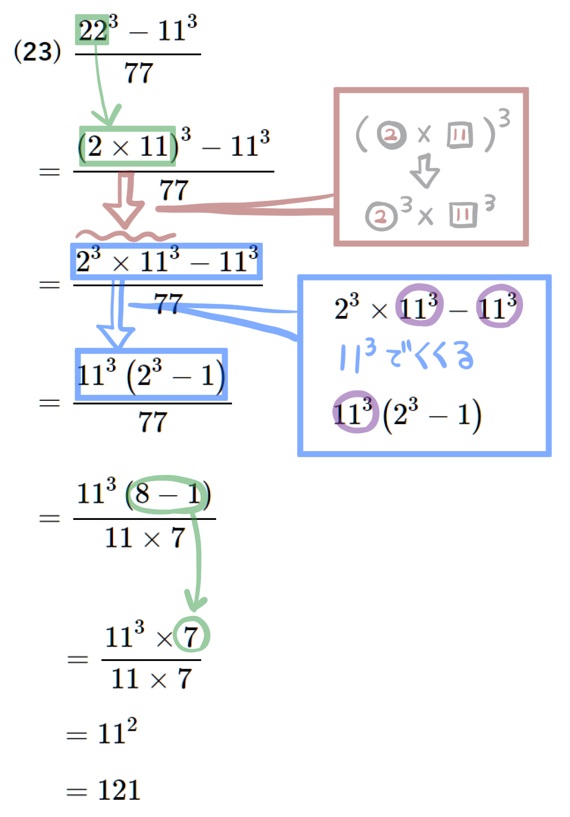
(24) \(11^{4}-11^{2}\times 120\)
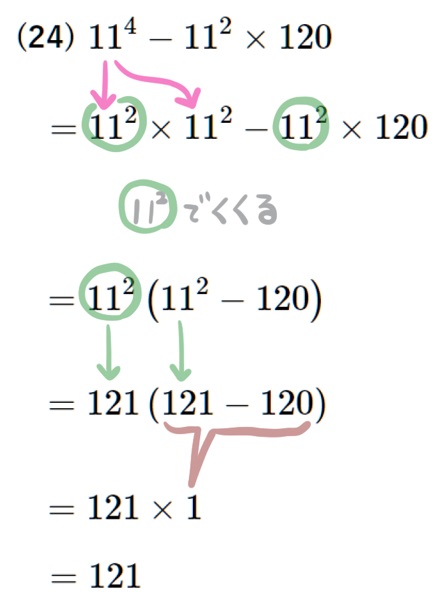
(25) \(\left( 13^{3}-7\times 13^{2}-6^{3}-7\times 6^{2}\right) \div 42\)
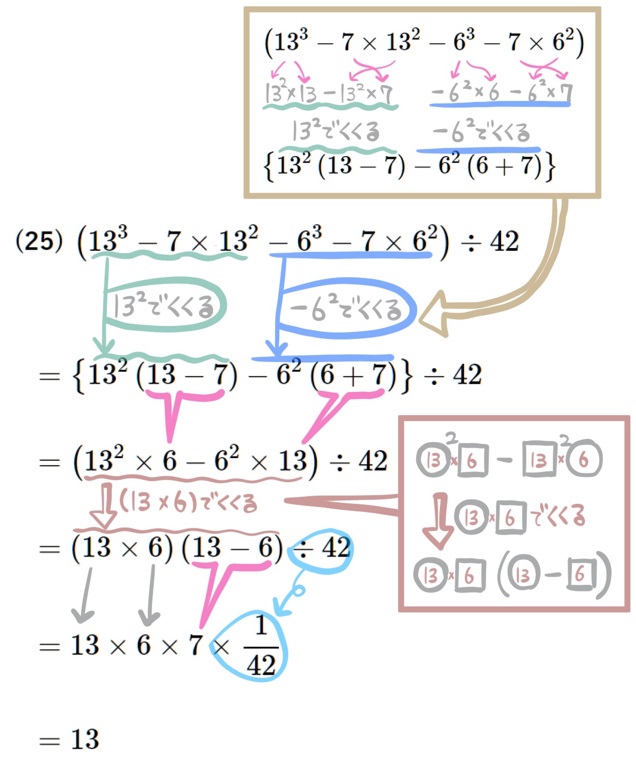

※セット版も単品版もあります。










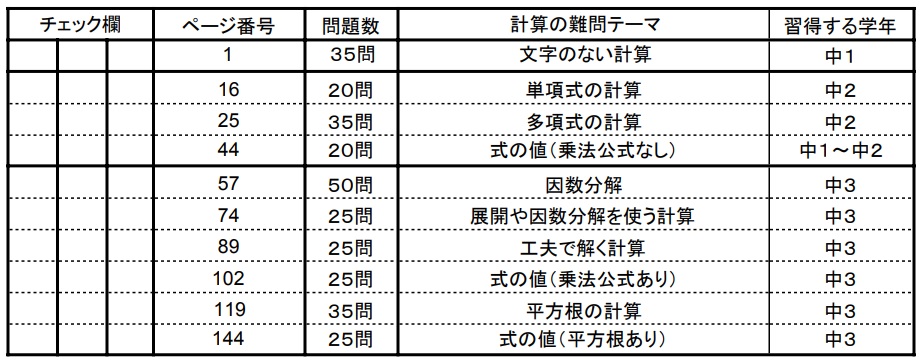
- 文字のない計算(正負の数の計算問題・四則演算)
- 単項式の計算(単項式の乗除)
- 多項式の計算問題の難問
- 式の値(乗法公式なし)
- 因数分解の難問
- 展開や因数分解を使う計算(多項式の計算)
- 工夫で解く計算問題(←学習したページ)
- 式の値(乗法公式あり)
- 平方根の計算問題の難問
- 式の値(平方根あり)




























