


- サイコロ2個での確率の練習問題|基本~標準
- サイコロ2個での確率の応用問題|難問
- サイコロ3個での確率の問題
- サイコロ4個または4回投げる確率の問題
基本~標準:サイコロを2個投げる確率の練習問題|中学数学レベル

- ab=12となる確率
- a+bが5の倍数となる確率
- \(a+b\)が素数となる確率
- abが奇数となる確率
- \(a+b\) が奇数となる確率
- \(a\leqq b\) となる確率
- \(\sqrt{ab}\) が整数となる確率
- \(\dfrac{a}{b}\) が整数となる確率
- 少なくとも1つの目が3以上となる確率
- 少なくとも1つの目が偶数となる確率
 異なる2個のサイコロを投げる場合、目の出方は全部で36通りあります。
異なる2個のサイコロを投げる場合、目の出方は全部で36通りあります。
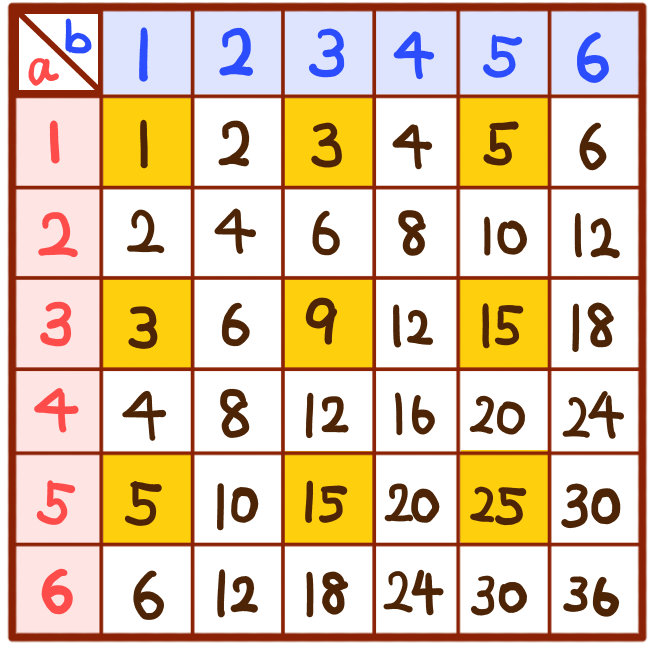
大のサイコロの目と小のサイコロの目の積を書き込んだ表をつくり、積が12となるマス目を数え上げます。

目の出方は全部で36通りあるので、確率は\(\dfrac{4}{36}=\dfrac{1}{9}\)ということです。


ここで紹介している練習問題を使い、高校入試までの対策をしてください。
 よって、\(\dfrac{7}{36}\) になります。
よって、\(\dfrac{7}{36}\) になります。 2から12までのなかで、素数は2,3,5,7,11になります。
2から12までのなかで、素数は2,3,5,7,11になります。
なので、二つのサイコロを振って、その和が素数になるのは15通り。
よって、\(a+b\)が素数になる確率は \(\dfrac{15}{36}=\dfrac{5}{12}\)
 答え: \(\dfrac{9}{36}=\dfrac{1}{4}\)
答え: \(\dfrac{9}{36}=\dfrac{1}{4}\)
奇数×奇数=奇数を利用して解くとこうなります。
大のサイコロの目が奇数になるのは1,3,5の3通り。
小のサイコロの目が奇数になるのは1,3,5の3通り。
よって2つのサイコロの目の積が奇数になるのは、3×3=9通り。
したがって、\(\dfrac{9}{36}=\dfrac{1}{4}\)
 答え:\(\dfrac{18}{36}=\dfrac{1}{2}\)
答え:\(\dfrac{18}{36}=\dfrac{1}{2}\)

二つのサイコロの目の数をたして奇数となるのは
偶数+奇数=奇数
奇数+偶数=奇数
となる場合である。
大のサイコロの目が奇数になるのは1,3,5の3通り。
小のサイコロの目が偶数になるのは2,4,6の3通り。
よって、大のサイコロで奇数の目が出て、小のサイコロで偶数の目が出る場合は
3×3=9通り
また
大のサイコロの目が偶数になるのは2,4,6の3通り。
小のサイコロの目が奇数になるのは1,3,5の3通り。
よって、大のサイコロで偶数の目が出て、小のサイコロで奇数の目が出る場合は
3×3=9通り
よって9通+9=10通りが求める場合の数になる。
したがって二つのサイコロを投げて目の和が奇数になる確率は\(\dfrac{18}{36}=\dfrac{1}{2}\)
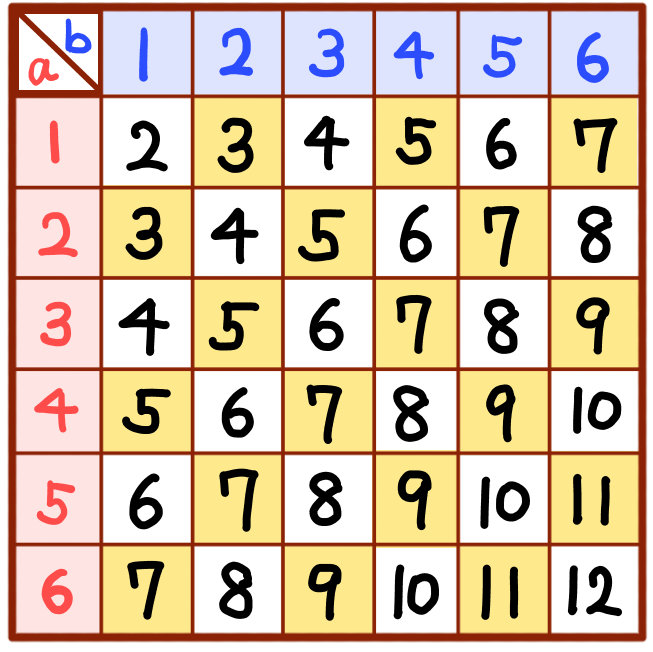
 aの目とbの目の数を比べて、二つの目の数が同じか、bの目のほうが大きい場合の数を数えます。
aの目とbの目の数を比べて、二つの目の数が同じか、bの目のほうが大きい場合の数を数えます。21通りありますので、求める確率は\(\dfrac{21}{36}=\dfrac{7}{12}\)
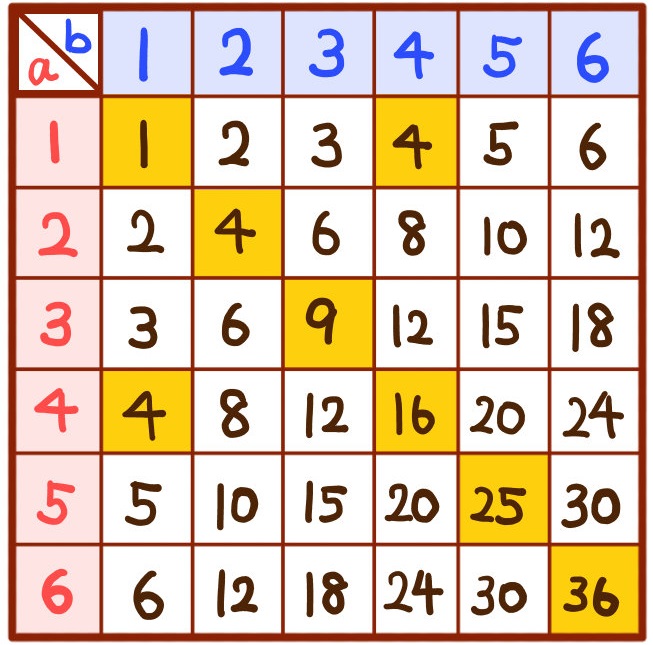 ルートabの値が整数となるためには、abの値が1,4,9,16,25,36のいずれかになればよい。
ルートabの値が整数となるためには、abの値が1,4,9,16,25,36のいずれかになればよい。
なので、その場合は上の表より、8通りとなる。
よってルートabの値が整数となる確率は \(\dfrac{8}{36}=\dfrac{2}{9}\)
 よって、 \(\dfrac{14}{36}=\dfrac{7}{18}\) となります。
よって、 \(\dfrac{14}{36}=\dfrac{7}{18}\) となります。
大小2つのサイコロの目を、問題文にしたがって分数にして考えます。
その際、分母がbなので、上の表で縦にそって\(\dfrac{a}{b}\) が整数になるかどうかのチェックをしていくとわかりやすいです。

なので中学数学でサイコロの確率の問題を対策する場合、このページで解説している練習問題を使って、『問題文を見ながら表を完成される練習』を繰り返してください。
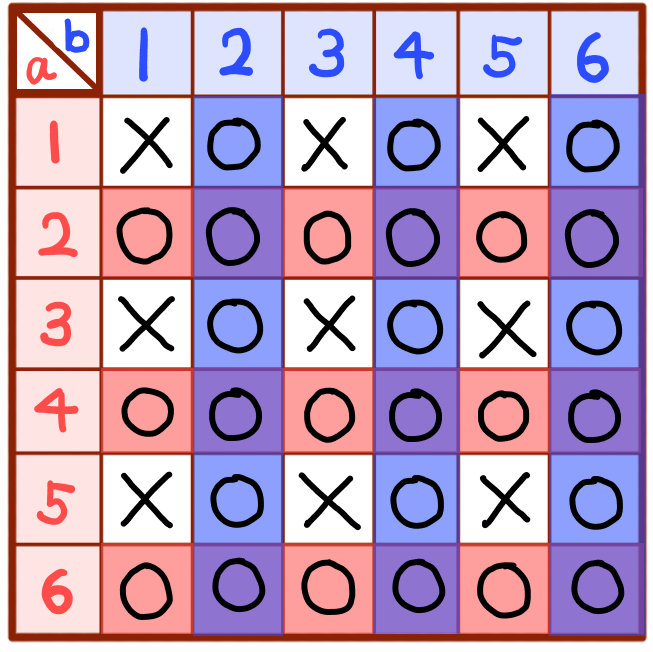
 赤い色のエリアが大のサイコロの目が3以上となる場合。
赤い色のエリアが大のサイコロの目が3以上となる場合。青い色のエリアが小のサイコロの目が3以上となる場合です。
よって、これらの色のついているエリアが、求める場合のところです。

しかし「少なくとも」という表現があった場合、『少なくとも1つの目が3以上となる場合以外(余事象)』は何通りあるかを数えたほうが早いことが多いです。
それはつまり『サイコロの目が両方とも2以下の場合』となります。
大のサイコロで1または2の2通り。
小のサイコロで1または2の2通り。
よって求める場合の余事象は2×2で4通りあることになります。
なので、36-4=32通りが求める場合の数になります。
(数え上げた結果と同じになりましたね。)

ちなみに、余事象が起こる確率は \(\dfrac{4}{36}\) なので、余事象が起こらない確率が求める確率となります。

\(1-\dfrac{4}{36}\)
\(=\dfrac{36}{36}-\dfrac{4}{36}\)
\(=\dfrac{36-4}{36}\)
\(=\dfrac{32}{36}\)
\(=\dfrac{8}{9}\)
 少なくとも1つの目が偶数となる場合の余事象は、両方のサイコロの目が奇数の目となる場合です。
少なくとも1つの目が偶数となる場合の余事象は、両方のサイコロの目が奇数の目となる場合です。
奇数の目は1,3,5の目しかありませんので、3通り×3通り=9通りとなります。

なので、それ以外の場合(求める場合の数)は36-9=27通りとなります。


\(1-\dfrac{9}{36}\)
\(=\dfrac{36}{36}-\dfrac{7}{36}\)
\(=\dfrac{36-9}{36}\)
\(=\dfrac{27}{36}\)
\(=\dfrac{3}{4}\)

- \(a+2b\) の値が3で割り切れる確率
- 出る目の数の最大公約数が2となる確率
- 出る目の数の最小公倍数が10以上となる確率
- \(\dfrac{a}{b}\leqq \dfrac{1}{2}\) となる確率
- aとbの差の絶対値が3より小さくなる確率
- 大のサイコロの目の数を十の位の数、小のサイコロの目の数を一の位の数として2桁の整数を作る。このとき、作った整数が7の倍数になる確率。
- \(a≦3<b\) となる確率
- \(4 <\sqrt{ab} <5\) となる確率
- \(\dfrac{3a}{b}\) が整数となる確率
- \(ab\) を3で割ると1余る確率

a+3bの値を表に書き込み、数え上げます。12通りですね。
bはあらかじめ3倍にしたもの、つまり3bの値の欄を準備しておくと計算が楽です。
よって、求める確率は\(\dfrac{12}{36}=\dfrac{1}{3}\) となります。
(八王子東高校)
 二つのサイコロの目の最大公約数を表に書き込むと上のようになります。
二つのサイコロの目の最大公約数を表に書き込むと上のようになります。
よって、求める確率は \(\dfrac{7}{36}\)
 二つのサイコロの目の最小公倍数を表に書き込むと上のようになります。
二つのサイコロの目の最小公倍数を表に書き込むと上のようになります。
よって、求める確率は \(\dfrac{12}{36}=\dfrac{1}{3}\)
 よって \(\dfrac{9}{36}=\dfrac{1}{4}\)
よって \(\dfrac{9}{36}=\dfrac{1}{4}\)
\(\dfrac{a}{b}\leqq \dfrac{1}{2}\) ということは、分子の値aが、分母の値bの半分以下ということです。


よってその確率は \(\dfrac{24}{36}=\dfrac{2}{3}\) となります。
 二桁の整数を書きならべ、順に調べる。
二桁の整数を書きならべ、順に調べる。

よって、求める2桁の整数が7の倍数になる確率は \(\dfrac{6}{36}=\dfrac{1}{6}\)
(大阪教育大学付属高校)
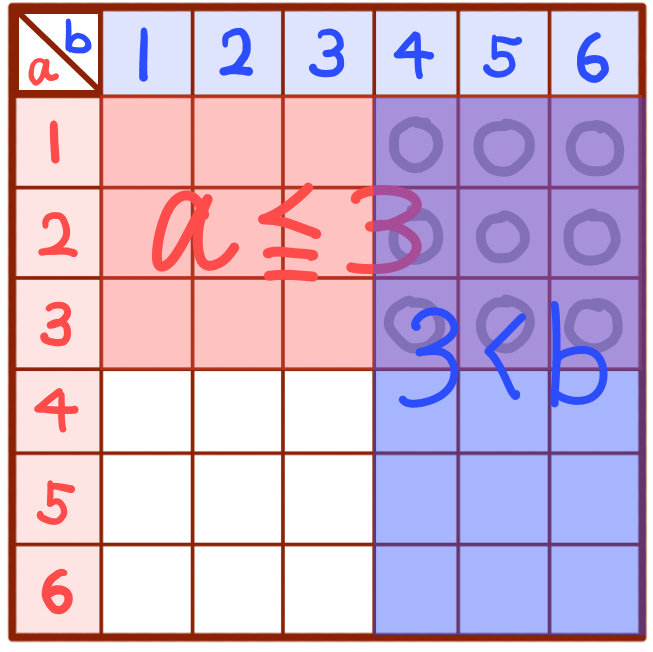 \(a≦3\)の場合は、赤色のエリアにあたります。
\(a≦3\)の場合は、赤色のエリアにあたります。
\(3<b\)の場合は、青色のエリアにあたります。
\(a≦3<b\)は、\(a≦3\)で、なおかつ\(3<b\)であるということなので、赤色と青色の共通するエリアの9通りが求める場合の数となります。
よってその確率は、\(\dfrac{9}{36}=\dfrac{1}{4}\)となる。
この場合、次のように処理をします。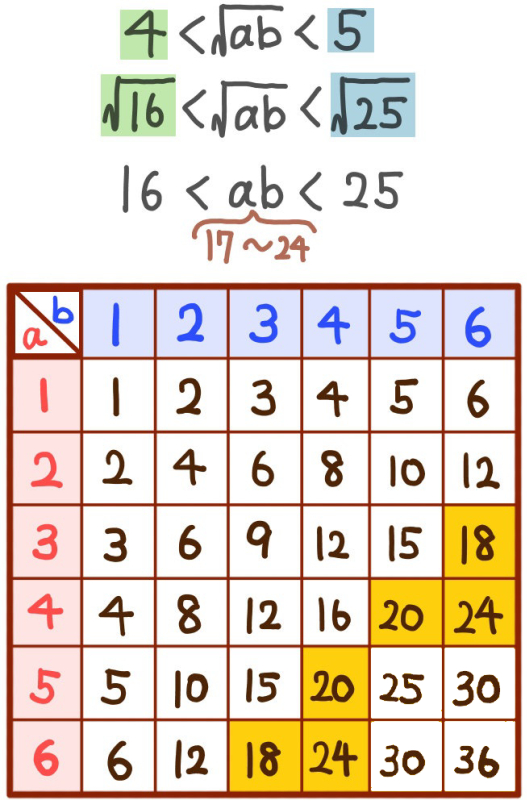 上のようにabの値が17から24までの場合を数えると6通りとなります。
上のようにabの値が17から24までの場合を数えると6通りとなります。
よって\(\dfrac{6}{36}=\dfrac{1}{6}\)


よって、36までの自然数でそのような数は
1、4、7、10、13、16、19、22、25、28、31、34
があります。
そうなるような場合の数を数えると下の表のようになります。
※ちなみに1は、3で割ると商は0で余りが1となります。

全部で8通りあるので、求める確率は\(\dfrac{8}{36}=\dfrac{2}{9}\)となります。
ここからは高校入試問題の対策となる難問レベルです。
難問:サイコロを2個投げる確率の応用問題|高校入試レベル
大小2つのサイコロを同時に投げ、大のサイコロで出た目をaとし、小のサイコロで出た目をbとする。次の確率を求めよ。
- 2直線 \(y=\dfrac{a}{b}x+3\) と \(y=2x+1\) が交わらない確率
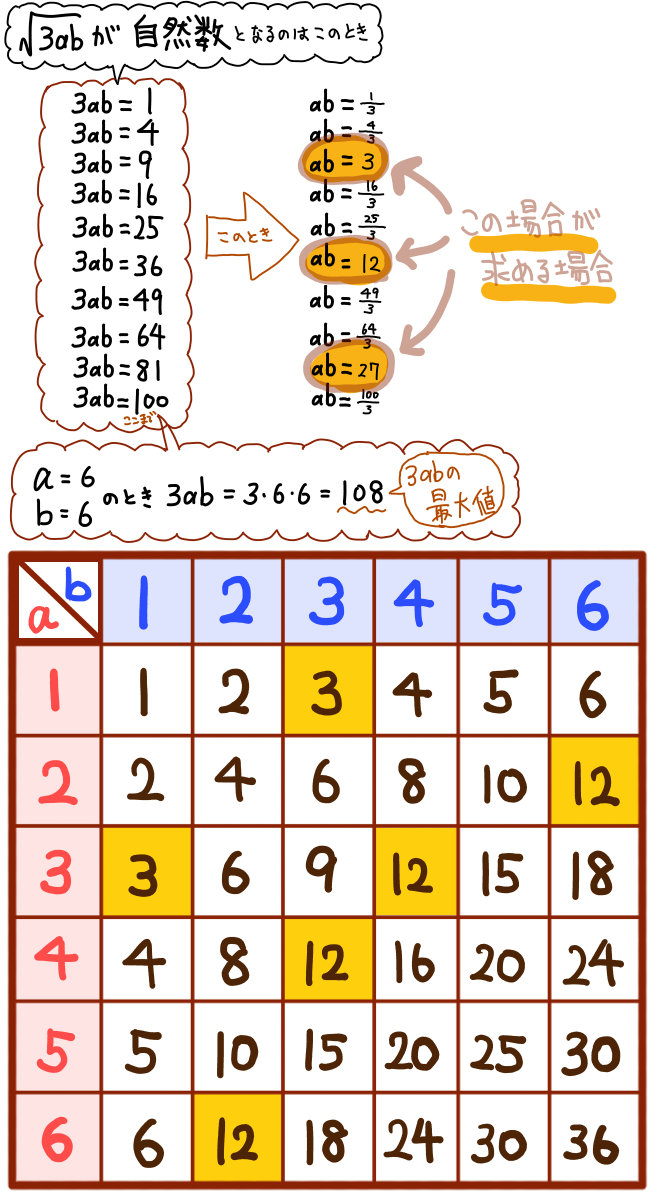
- \(\sqrt{3ab}\) が自然数となる確率
- \(ab+a+b+1\)が3の倍数となる確率
- \(ab-a-3b+3\) が自然数となる確率
- \(a^{2}+2ab+b^{2}\) が奇数となる確率
「2直線が交わらない」とは「2直線が平行かつy切片の値が異なる」ということです。
2直線のy切片はすでに異なっているので、2直線が平行になる場合だけを調べればよい、ということになります。
2直線が平行になる場合というのはつまり、 \(\dfrac{a}{b}\) の値が2になる場合のことです。


よって、 \(\dfrac{3}{36}=\dfrac{1}{12}\) が答えとなります。
(明治学院高校:改)

よって、\(\dfrac{6}{36}=\dfrac{1}{6}\)
こんな数え方もあります。ただし、最初の解法のほうが数え上げる手間が省けるのでおすすめです。
 まず、\(ab+a+b+1\)を因数分解して積の形に変形します。
まず、\(ab+a+b+1\)を因数分解して積の形に変形します。
(a+1)(b+1)が3の倍数になればいいということは、サイコロを振って出た目aに+1した目の値と、出た目bに+1した目の値の積が3の倍数になればいいということです。

基本的に中学数学では、確率を習ったあとに因数分解を学習するので、定期テストでこのような高校入試問題の対策ができる機会は比較的少なくなってしまいます。
高校入試で出されたサイコロの確率の問題を実際に解くことで、勉強がまだ足りていない弱点等に気が付くことができます。
(明訓高校の高校入試問題より)
 よって、答えは\(\dfrac{15}{36}=\dfrac{5}{12}\) となります。
よって、答えは\(\dfrac{15}{36}=\dfrac{5}{12}\) となります。
これも先程と同じ手順でクリアできます。
中学数学で学習するサイコロの確率の問題のなかでは難問の類ではありますが、一度解き方のパターンに慣れてしまえば、途中で詰まるところはない良問です。
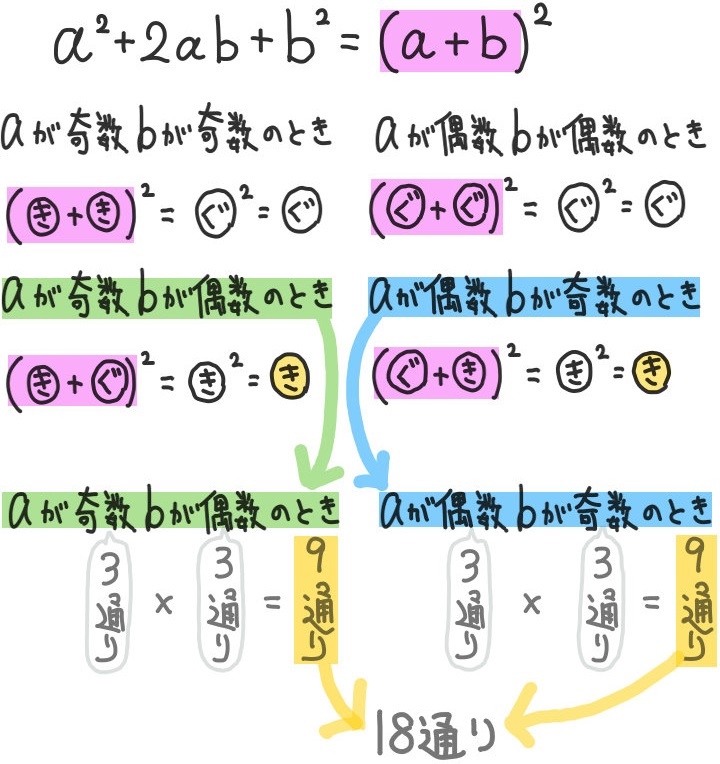 よって、\(\dfrac{18}{36}=\dfrac{1}{2}\)
よって、\(\dfrac{18}{36}=\dfrac{1}{2}\)
表に書いて数え上げようとすると手間と時間がかかってしまう難しいタイプの出題内容です。
偶数と奇数の性質に着目して、場合の数を調べる必要がある難問です。
基礎~難問:サイコロを3個投げる確率の問題|中学数学~高校入試
大中小のサイコロ3つを同時に投げる。このとき、次の確率を求めよ。
基本:3つのサイコロの目の積が偶数となる確率

奇数を「き」と書いて、偶数を「ぐ」を書いて説明しています。




基本:3つのサイコロの目の和が偶数となる確率
 3のサイコロを投げてその目の和が偶数になるのは次の2パターンあります。
3のサイコロを投げてその目の和が偶数になるのは次の2パターンあります。
1:3個とも偶数の目が出た場合
2:1個だけ偶数の目が出て、残りの2個で奇数の目が出た場合
それらの各場合について、求めることになります。
基本:少なくとも2つの目が同じになる確率
大のサイコロの目の出方は、全部で6通り
中のサイコロの目の出方は、大のサイコロで出た目以外の5通り
小のサイコロの目の出方は、大と中のサイコロで出た目以外の4通り
よって、「出た目のすべてが異なる目である場合」は6×5×4通り。
3つのサイコロの目の出方は \(6^{3}\)
出た目のすべてが異なる目となる確率は\(\dfrac{6\times 5\times 4}{6^{3}}=\dfrac{5}{9}\)
よって、求める確率は \(1-\dfrac{5}{9}=\dfrac{4}{9}\)
(桐蔭学園高校)
標準:出た目の数の和が5以下になる確率

3つのサイコロの出た目の和が3のとき
(1,1,1)
の1通り。
3つのサイコロの出た目の和が4のとき
(1,1,2)
(1,2,1)
(2,1,1)
の3通り。
3つのサイコロの出た目の和が5のとき
(1,1,3)
(1,3,1)
(3,1,1)
(1,2,2)
(2,2,1)
(2,1,2)
の6通り。
出た目の合計が5以下になるのは1+3+6=10通り
サイコロを3つ投げた場合の目の出方は全部で \(6^{3}\) 通り
よって \(\dfrac{10}{6^{3}}=\dfrac{5}{108}\)
(東大寺学園高校)
難問:大中小3つのサイコロを同時に投げ、出た目をそれぞれa、b、cとするとき、\(3a-2b-c=0\) となる確率
それらが1から6の整数値の場合のみ、それがcの値として方程式が成立することができます。


よって、求める確率は\(\dfrac{12}{36}=\dfrac{1}{3}\)
(函館ラ・サール高校)
サイコロを4個または4回投げる確率の高校入試問題
-
サイコロを4回続けて投げるとき、次の確率を求めなさい。
- すべて同じ目になる確率
- すべての目が異なる確率
- 1回目、2回目、3回目、4回目の順に、出る目が大きくなる確率
- 1の目と2の目がそれぞれ2回ずつ出る確率
- 1回だけ異なる目が出る確率
- 出る目が2種類になる確率
(1,1,1,1)
(2,2,2,2)
(3,3,3,3)
(4,4,4,4)
(5,5,5,5)
(6,6,6,6)
の6通り。
サイコロを4回投げた場合の目の出方は全部で \(6^{4}\) 通り。
よって、求める確率は \(\dfrac{6}{6^{4}}=\dfrac{1}{216}\)
2回目のサイコロの目は、1回目のサイコロで出た目以外の5通り
3回目のサイコロの目は、1回目と2回目のサイコロで出た目以外の4通り
4回目のサイコロの目は、1回目から3回目のサイコロで出た目以外の3通り
よって、すべての目が異なるのは
6×5×4×3=360通り
サイコロを4回投げた場合の目の出方は全部で \(6^{4}\) 通り。
したがって求める確率は、 \(\dfrac{360}{6^{4}}=\dfrac{5}{18}\)
(1,2,3,4)
(1,2,3,5)
(1,2,3,6)
(1,2,4,5)
(1,2,4,6)
(1,2,5,6)
(1,3,4,5)
(1,3,4,6)
(1,3,5,6)
(1,4,5,6)
(2,3,4,5)
(2,3,4,6)
(2,3,5,6)
(2,4,5,6)
(3,4,5,6)
の15通りあります。
サイコロを4回投げた場合の目の出方は全部で \(6^{4}=1296\) 通りです。
なので、求める確率は \(\dfrac{15}{1296}=\dfrac{5}{432}\) となります。
1の目と2の目がそれぞれ2回ずつ出るのは
(1,1,2,2)
(1,2,1,2)
(1,2,2,1)
(2,1,1,2)
(2,1,2,1)
(2,2,1,1)
の6通りある。
よって求める確率は \(\dfrac{6}{6^{4}}=\dfrac{1}{216}\)
異なる目を異
と表記すると
「同」になる目としては全部で6通りあり
「異」になる目は「同」の目以外の5通りあります。
なので、
「同」と「異」の目の組み合わせは全部で6×5=30通りあります。

この30通りの「同」と「異」の目の組み合わせ対して、次の4パータンの「目の出る順番の組み合わせ」があります。
(同,同,同,異)
(同,同,異,同)
(同,異,同,同)
(異,同,同,同)

(6,6,6,2)
(6,6,2,6)
(6,2,6,6)
(2,6,6,6)
の4パターンあるワケです。
なので、求める場合の数は、全部で30×4=120通りあります。
よって、求める確率は \(\dfrac{120}{6^{4}}=\dfrac{5}{54}\) となります。
(立教新座高校)
AとBの目の組は
Aが1から6までの6通り
BがAで出た目以外の5通り
よって6×5=30通りある。
この30通りに対して、「出る目が2種類になる」目の出方が次の7通りある。
1回だけ異なる目が出る場合
AAAB
AABA
ABAA
BAAA
2回ずつ2種類出る場合
AABB
ABBA
ABAB
よって、出る目が2種類になるのは30×7=210通り
求める確率は \(\dfrac{210}{6^{4}}=\dfrac{35}{216}\)
(慶応義塾志木高校)

1回だけ異なる目が出る場合
AAAB
AABA
ABAA
BAAA
だけでなく、さらに追加して
BBBA
BBAB
BABB
ABBB
2回ずつ2種類出る場合
AABB
ABBA
ABAB
だけでなく、さらに追加して
BBAA
BAAB
BABA

AAABの場合を考えると
例えば
A=3、B=4のとき「3334」となり、
A=4、B=3のとき「4443」となります。
なので、BBBAの場合まで含めて計算する必要はありません。
AABBについても同様です。
例えば
A=3、B=4のとき「3344」となり、
A=4、B=3のとき「4433」となります。
なので、BBAAの場合まで含めて計算する必要はありません。
ABBAについても同様です。
例えば
A=3、B=4のとき「3443」となり、
A=4、B=3のとき「4334」となります。
なので、BAABの場合まで含めて計算する必要はありません。
ABABについても同様です。
例えば
A=3、B=4のとき「3434」となり、
A=4、B=3のとき「4343」となります。
なので、BABAの場合まで含めて計算する必要はありません。






























大のサイコロで出た目をaとする。
小のサイコロで出た目をbとする。
ただし、2つのサイコロは、どの目が出る確率も同様に確からしいものとする。