


- 1次関数のグラフの応用問題や難問
- 1次関数のグラフの応用問題の解き方とおすすめ反復方法
1次関数のグラフの応用問題や難問|定期テスト対策~高校入試対策
図のように、関数\(y=\dfrac{a}{x}\) のグラフ上に3点A、B、Cがある。
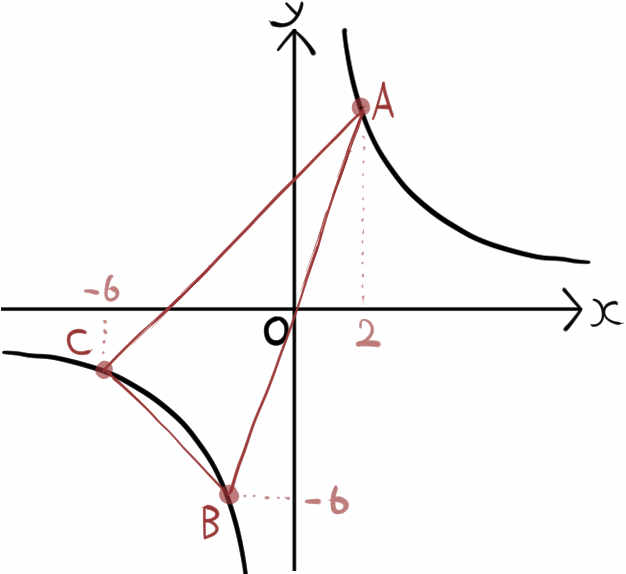
点Aと点Bは原点Oに対して点対象であり、
点Aのx座標は2
点Bのy座標は−6
点Cのx座標は−6である。
このとき、△ABCの面積を求めなさい。
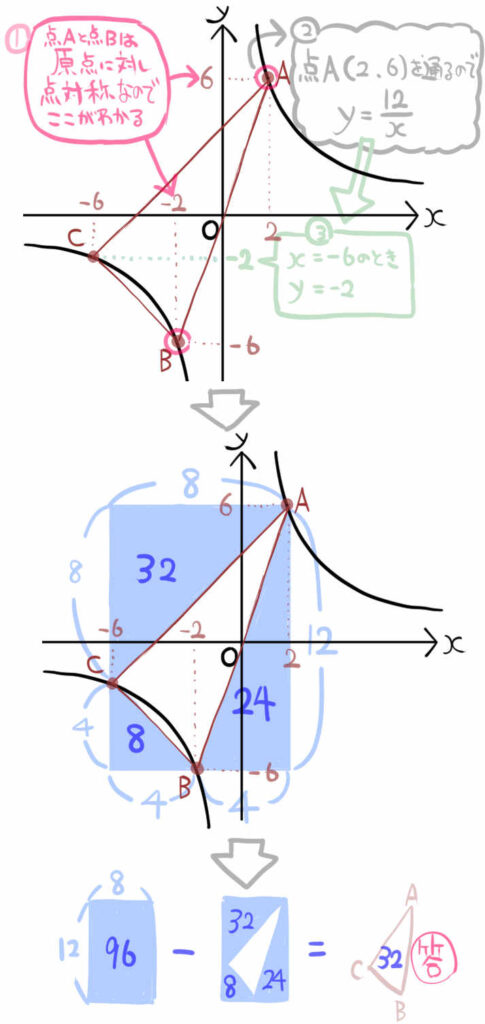
最初に定数aを求めたいところですが、情報が足りません。
点Aと点Bが原点Oに対して点対称なのでは?と気が付くところが突破口になります。
1次関数\(y=2ax-3\) と
1次関数\(y=2bx+a+1\)のグラフが
交点\(\left( -1,b\right) \)を作るとき
定数a、bの値を求めなさい。
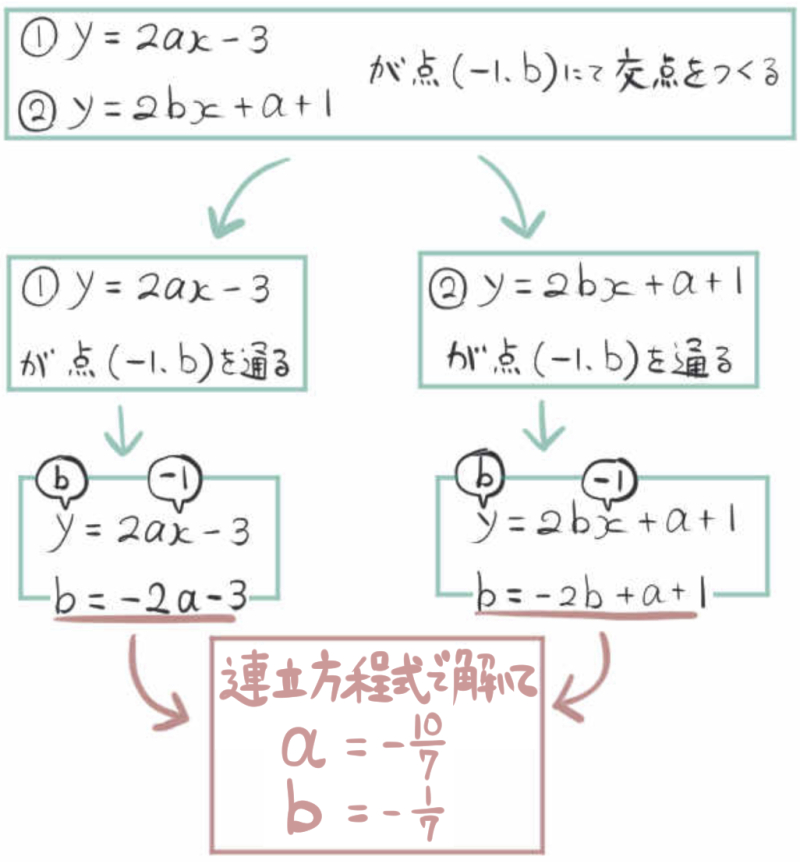
「交点を作る」ということは、1次関数のグラフはその交点の座標を通るということです。
なので、1次関数の式にその交点の座標を代入しても、できあがった等式は成り立ちます。
一次関数\(y=ax+2a+7\) (a <0)のグラフについて
xの変域が\(-5\leqq x\leqq 2\)であるとき
yの変域が\(3\leqq y\leqq 2b\) となるような
定数a、bの値を求めなさい。
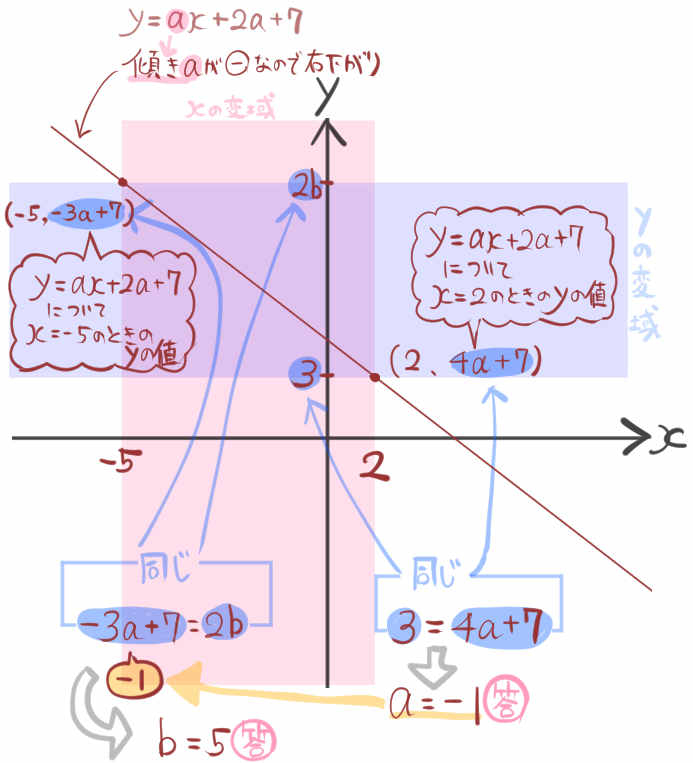
このような変域の問題は、変域をグラフに書き込んでから、求める一次関数がどのように書くことができるのか、という予測を立てます。この問題の場合、一次関数の傾きの符号までわかっているので、それも予測に利用します。
次の2つの条件を同時に満たす直線の式を求めなさい。
条件1:一次関数のグラフ\(y=\dfrac{1}{2}x-6\)との交点のx座標が8である。
条件2:x軸との交点のx座標が4である。
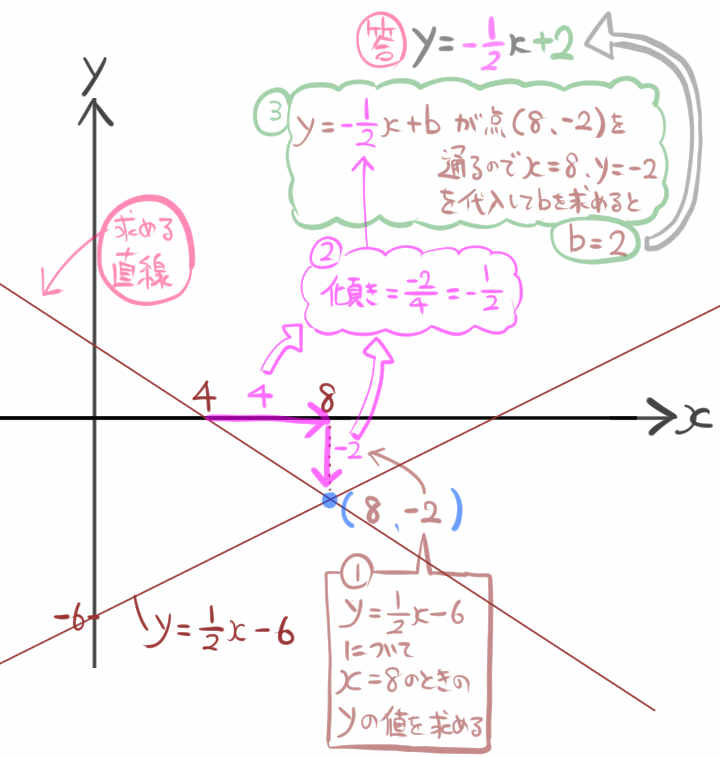
基本的に一次関数のグラフの問題はグラフを書いて、それを見ながら考えます。
解説に書かれてある①②③の手順で明らかにしていきます。
次の3つの直線について考える。
\(y=\dfrac{1}{2}x+6\)
\(y=x\)
\(y=ax\) (aは定数)
この3つの直線によって作られる三角形の面積が48であるとき、定数aの値を求めなさい。
ただしa<0とする。
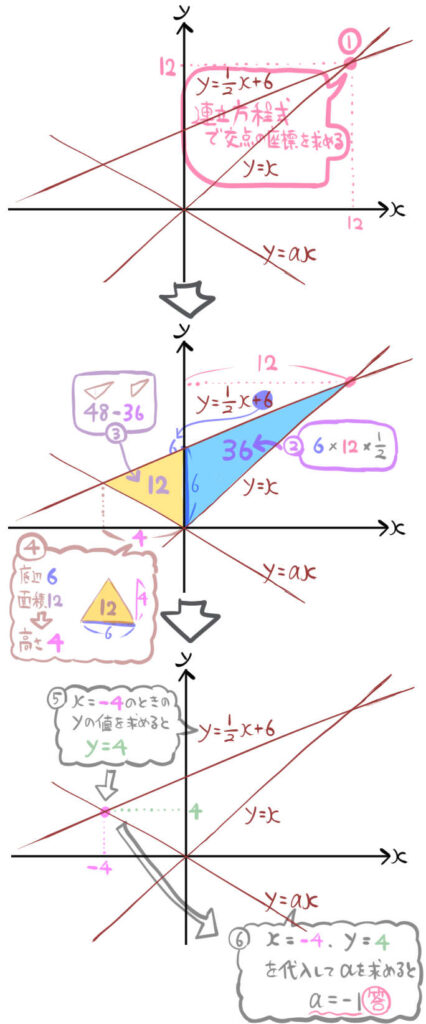
まずは、3本の直線をグラフを書いてみましょう。 \(y=ax\)の定数aが負の値なので、原点を通り、かつ右下がりのグラフであるというポイントをおさえておけば、だいたいのグラフでいいです。
座標平面上において、x座標、y座標ともに整数である点を格子点という。例えば点(2,3)は格子点である。
直線 \(y=-\dfrac{1}{2}x+\dfrac{5}{2}\) より下側にある格子点の座標をすべて求めよ。
ただし、直線 \(y=-\dfrac{1}{2}x+\dfrac{5}{2}\) 上の点を含み、 格子点のx座標、y座標ともに正の数であるものとする。
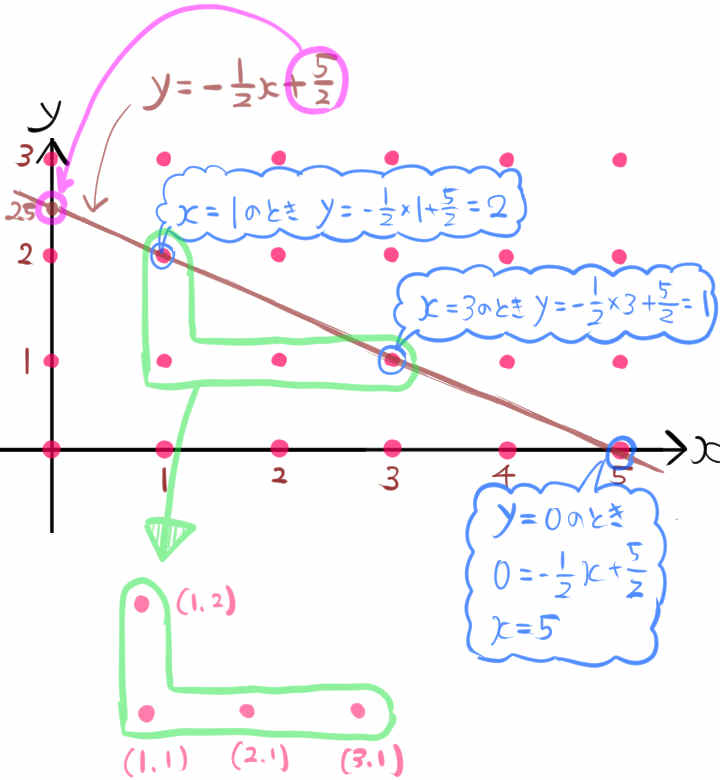
\(\dfrac{5}{2}\) が5の半分、つまり2.5なので、1次関数\(y=-\dfrac{1}{2}x+\dfrac{5}{2}\) のグラフは、y切片が2.5である右下がりのグラフとなります。それをまずは書きましょう。そのグラフの下側にある、x座標が正の整数である格子点について調べることとなります。
\(y=-\dfrac{1}{2}x+3+b\) が格子点(1、n)を通る。定数bがとりうる最小の値と、このときの整数nの値を求めなさい。ただしb>0とする。
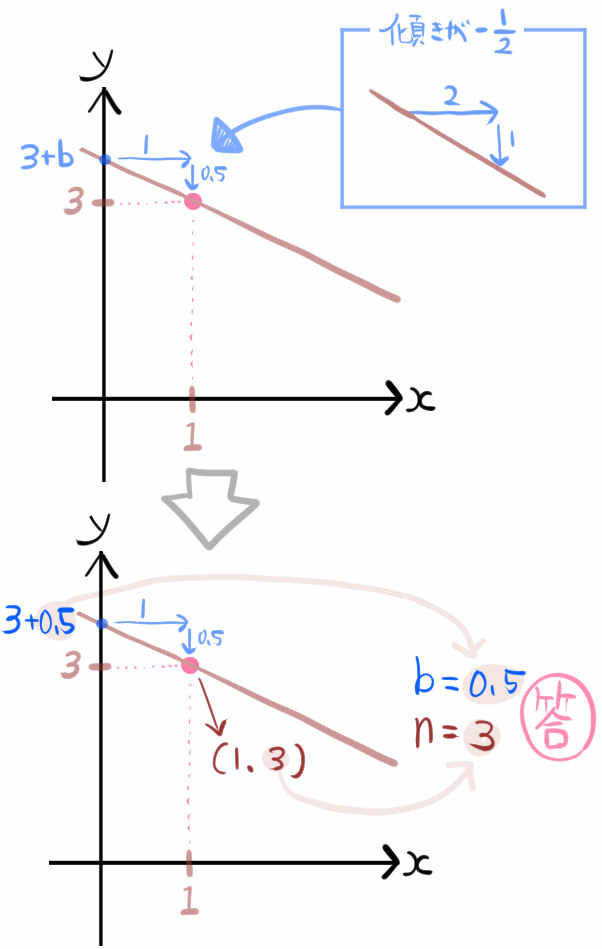
3+bがy切片である1次関数\(y=-\dfrac{1}{2}x+3+b\) のグラフをまずは書きます。
このグラフが通る格子点のx座標が1であるということから、グラフとy軸との交点(0、3+b)から、xが1増加したときのyの増加量について考えます。
傾きが \(-\dfrac{1}{2}\) なので、xが1増加したときのyの増加量は-0.5となります。
つまり、点(0、3+b)からxが1増加し、yが-0.5増加したときの座標が(1、3)になる場合が、bが最小の値をとる場合です。
次の3つの一次関数のグラフによって三角形が作られないような定数aの値をすべて求めなさい。
\(y=2x-4\)
\(y=-\dfrac{1}{3}x+3\)
\(y=ax\)
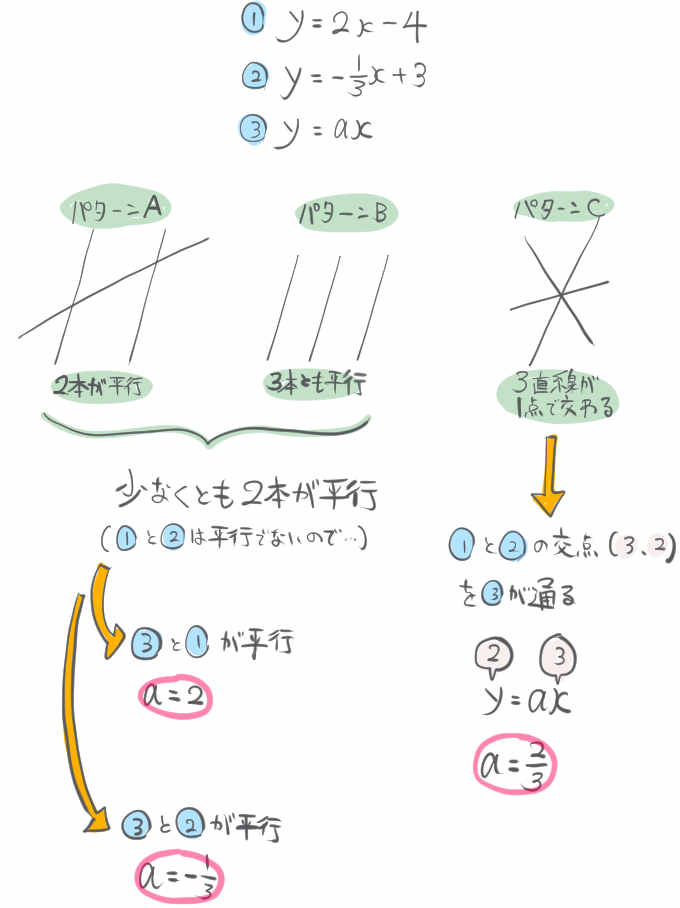
もし、初見の状態で試験本番でこの問題に出くわしたら、まずこのようにします。
3本の直線が三角形を作らないパターンというのは、どのようなパターンが考えられるか?を整理します。
1次関数のグラフの応用問題の解き方とおすすめ反復方法






























グラフを書いたあとで、「何に注目したのか」「何に気が付いたのか」「どんな予測が立ったのか」「何を試したのか」などの経験値を積むことが実力UPにつながります。
また、しっかり反復してある問題のストックがあれば、「あの問題と似ているかも」と、気が付くことも増えてくるでしょう。
ここで練習した問題は、そこまで「激ムズ」というほどの問題ではありません。(初見の場合はもちろん戸惑う問題もあります)
これぐらいのレベルの応用問題や難問は、ちょっと考えてわからなければ解答を見て、思考パターン、解法パターンのストックとして利用してください。
自分のなかでストックにするためには、反復が必要です。
手を動かして何周もすると時間がかかりまくるので、解法の図を見ながら口頭で自分に説明してあげてください。
この方法は、「解法の流れ」を府に落としやすいですし、時間短縮にもなり、かなりおすすめです。
また、復習や反復をせずに解き散らかすのはおすすめできません。
もし、手元に繰り返し愛用している問題集があるなら、そちらを反復しまくるほうが断然効率がいいです。
ここで習得できていない問題パターンだけ、ノートに写すなりして、反復用に加えるというのなら大丈夫です。