



因数分解の文章問題7選|中学数学~高校入試
(1) \(x^{2}-2x+1\) を因数分解した結果を利用し、 \(x^{2}-2x-8\)を因数分解せよ。
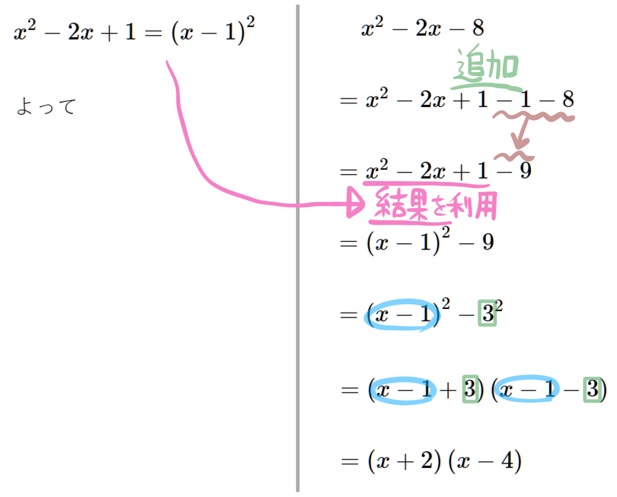
このように結果のかたちを利用して解くというのは誘導問題のある出題でよく使います。
(2) \(\left( a+b+1\right) ^{2}\)を展開した結果を利用し、 \(-3a^{2}+b^{2}+2ab+2a+2b+1\) を因数分解せよ。

先程と同じ発想で、+■⁻■というように、合計が0となるセットを追加して式変形すると作りやすいです。
(3) \(\dfrac{n\left( n+1\right) }{2}-\dfrac{\left( n-1\right) n}{2}\) を因数分解した結果を利用し、次の式を計算せよ。
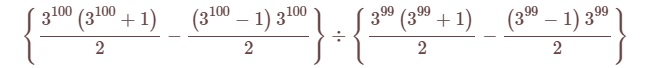
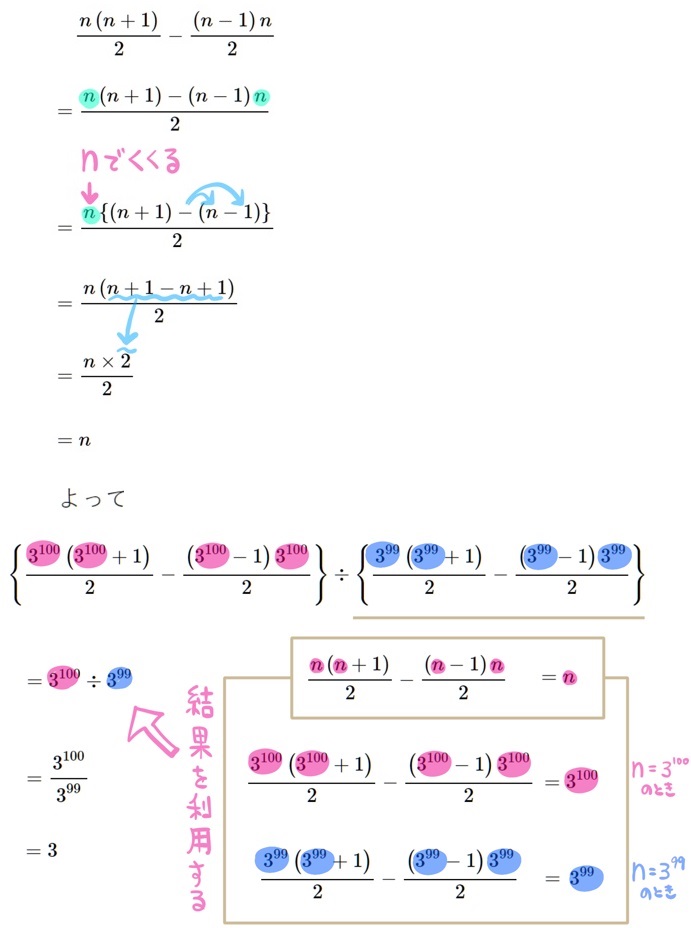
この問題の場合は、nが3の100乗である時と、nが3の99乗である時の2通りにおきかえています。
(4) \({\small \dfrac{n\left( n+1\right) \left( n+2\right) }{3}-\dfrac{\left( n-1\right) n\left( n+1\right) }{3}}\) を因数分解した結果を利用し、次の式を計算せよ。
\({\small 1\times 2+2\times 3+3\times 4+\ldots +28\times 29}\)

それを利用し、計算せよと指示された式を変形します。
すると、打ち消し合って和が0になる異符号の項が表れてゆくということに気が付きます。
どのように打ち消し合うか?という法則性に注目すると、最後にどこの項が残るかということがわかります。
(5) \(x^{2}+4x+b\) を因数分解すると、 \(\left( x+8\right) \left( x-a\right) \) となる。定数a、bの値をそれぞれ求めよ。

xの係数と定数項の部分がそれぞれ同じであることから、方程式を作ることができます。
(6) \(\left( ax-2y\right) \left( x+3by\right) \) を展開した結果、 \(x^{2}+4xy-cy^{2}\) となった。定数a、b、cの値をそれぞれ求めよ。
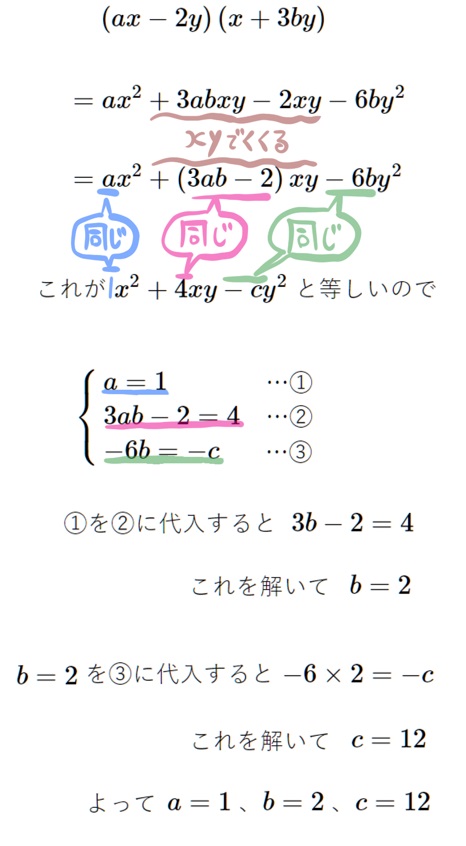
因数分解された形を展開し、各項の係数を比較します。
(7) \(1+2+3+\ldots +99\) の結果を利用し、 次の式を計算せよ。
\({\small \left( 1^{2}-2^{2}\right) +\left( 3^{2}-4^{2}\right) +\ldots +\left( 98^{2}-99^{2}\right)} \)

求めたい数列の2倍の値をまず求めてから、それを半分にするという計算方法です。
次に、この数列の和の結果を利用するために、同じ数列のかたちを取り出すことを考えます。
まずは「2乗-2乗」という並びが続いていますので、因数分解により変形してみると、突破口が見えてきます。

※この内容は特典として追加しています。








因数分解の文章問題の考え方のコツ

ここで用意した問題は「~を因数分解した結果を利用し」という言い回しがありますが、高校入試本番では、これが1つの小問となっていることが多いということです。
これを解き、2問目でそれを利用するという構成になっていると思ってください。
「誘導問題の結果を利用して次の問題を解く」という文章題の場合、主に次の3通りの使い方があります。
- 同じかたちを作り出し、式変形する。
例:(1)(2)(7)の問題 - 文字に値を代入する。
例:(3)(4)の問題 - 係数を比較する。
例:(5)(6)の問題




























