


平方根が日常生活で使われている例(カメラ)

F1.4
F2.0
F2.8
F4.0
F5.6
F8.0





平方根を日常生活で活用する具体例(面積の大きさ)


横bセンチメートル
の紙の面積(広さ)は
ab平方センチメートルです。
では、「この2倍の面積は?」
と質問されたら、当然「2ab平方センチメートルです」と答えますね。
では、「面積が2ab平方センチメートルになるためは、縦と横の長さは何であればいいですか?」
と質問されたら次のような回答が出ることでしょう。
横2bセンチメートル
面積\(a\times 2b=2ab\)平方センチメートル

横bセンチメートル
面積\(2a\times b=2ab\)平方センチメートル


縦1.5aセンチメートル
横\(\dfrac{4}{3}b\)センチメートル
面積\(1.5a\times \dfrac{4}{3}b=\dfrac{15}{10}a\times \dfrac{4}{3}b=2ab\)平方センチメートル

縦\(\sqrt{2}a\)センチメートル
横\(\sqrt{2}b\)センチメートル
面積\(\sqrt{2}a\times \sqrt{2}b=2ab\)平方センチメートル

これが方程式ですね。
左辺を整理すると
\(abx^{2}=2ab\)
aもbも0ではないので、abは0ではありません。
なので両辺をabで割ると
\(x^{2}=2\)
xは正の数なので
\(x=\sqrt{2}\)
と、求めることができます。
(xが正の数であるという理由:xが負の値であったら、それをかけあわせてできた縦、横の長さは負の数になります。長さが負の数になることは現実世界では考えられないので、負の数は除外するということです。)





円の面積は、半径×半径×円周率なので、半径を\(\sqrt{2}\)倍すると、面積は2倍になります。
半径をr、円周率をπとして、確認してみましょう。
半径を\(\sqrt{2}\)倍する前の円の面積
\(r\times r\times \pi =\pi r^{2}\)
半径を\(\sqrt{2}\)倍した後の円の面積
\(\sqrt{2}r\times \sqrt{2}r\times \pi =2\pi r^{2}\)
ちゃんと面積は2倍になっていますね。


↓\(\sqrt{2}\)倍
F1.4
↓\(\sqrt{2}\)倍
F2.0
↓\(\sqrt{2}\)倍
F2.8
↓\(\sqrt{2}\)倍
F4.0
↓\(\sqrt{2}\)倍
F5.6
↓\(\sqrt{2}\)倍
F8.0



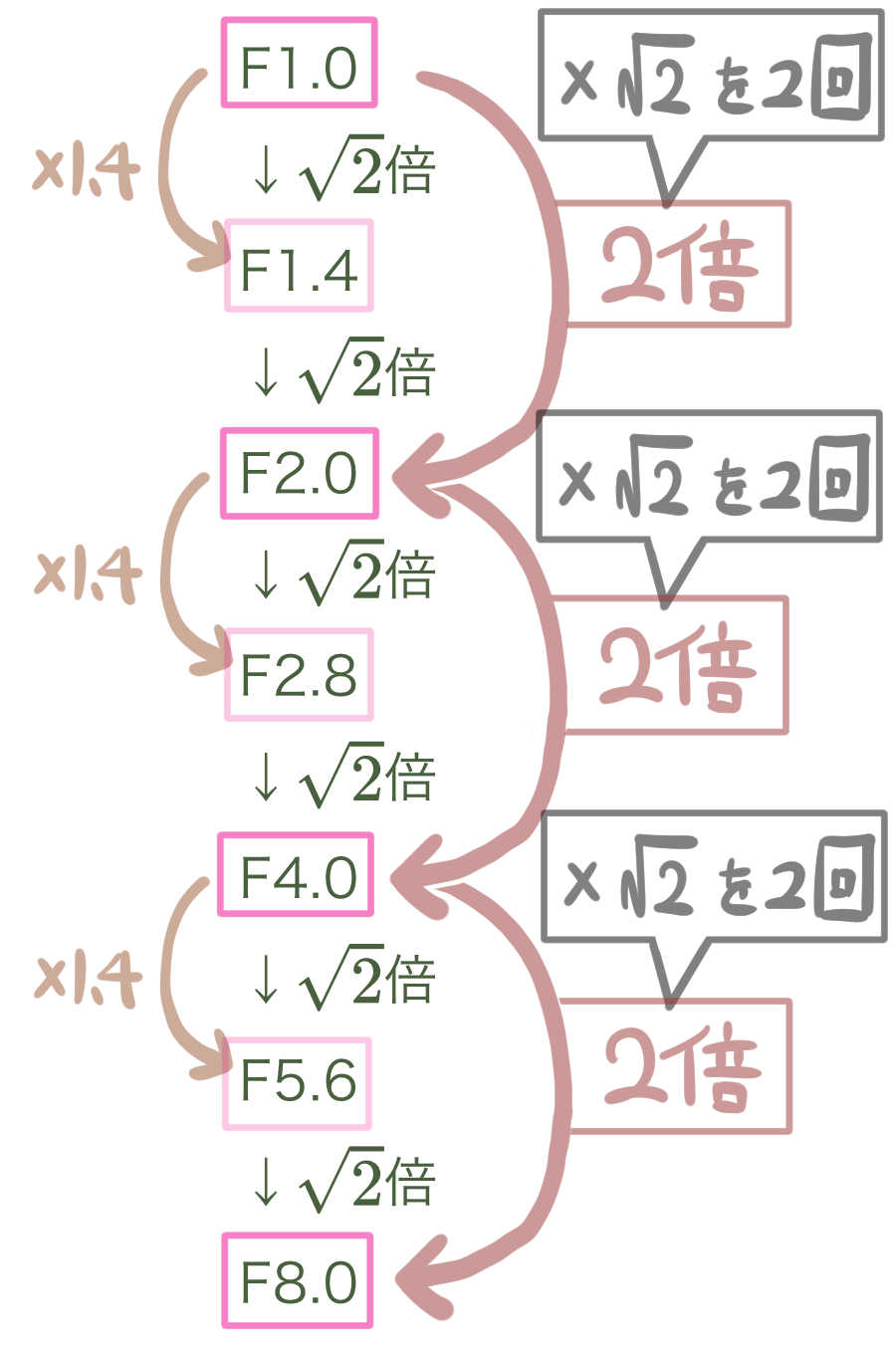
カメラのF値には、このように平方根が使われています。
カメラの例から学べる平方根の活用例


1:正方形や長方形の面積をn倍にしたい場合、縦、横の長さをともに\(\sqrt{n}\)倍すればよい。
2:円の面積をn倍にしたい場合、半径の長さを\(\sqrt{n}\)倍すればよい。
3:三角形や平行四辺形の面積をn倍にしたい場合、高さ、底辺の長さをともに\(\sqrt{n}\)倍すればよい。(同じ方法で確認できます)
以上のように、平方根の活用例は面積に関する話になりましたが、3乗根(高校で学習します)は体積をテーマに活用例を考えることができます。
例:ある立方体の体積を2倍にしたい場合、縦a、横b、高さcの長さをそれぞれ\(\sqrt[3] {2}\)倍すればよい。
すると体積は\(\sqrt[3] {2}a\times \sqrt[3] {2}b\times \sqrt[3] {2}c=2abc\)となり、元の体積abcの2倍となる。
※円錐でも球体でも同じように考えることができます。





























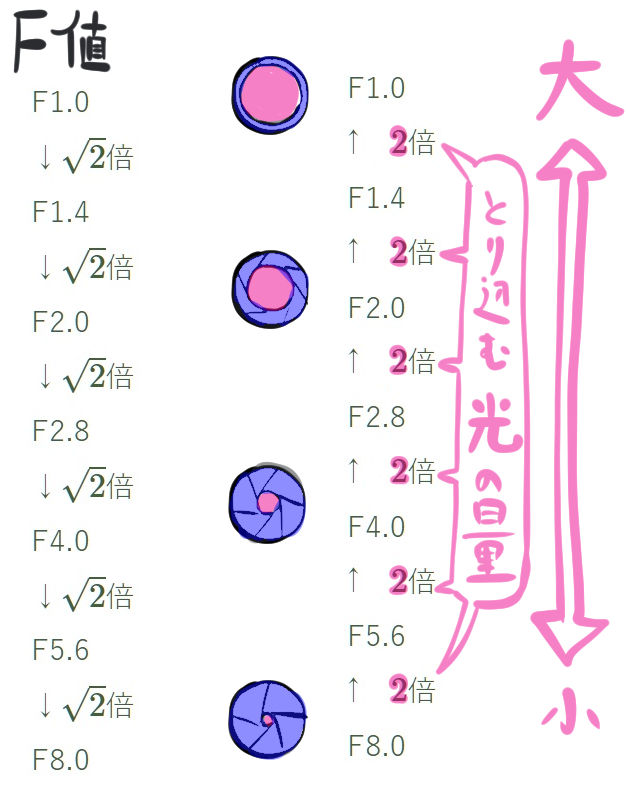
カメラはシャッターボタンを押した際に光を取り込んで撮影します。
この光の量をどれだけ取り込むかという調節をすることで写り方を変えることができます。
また、カメラのレンズには穴の大きさを調整する絞り値(F値)というものがあります。
このF値を変更することで写り方を変えることができるのですが、F値はこのようになっています。