



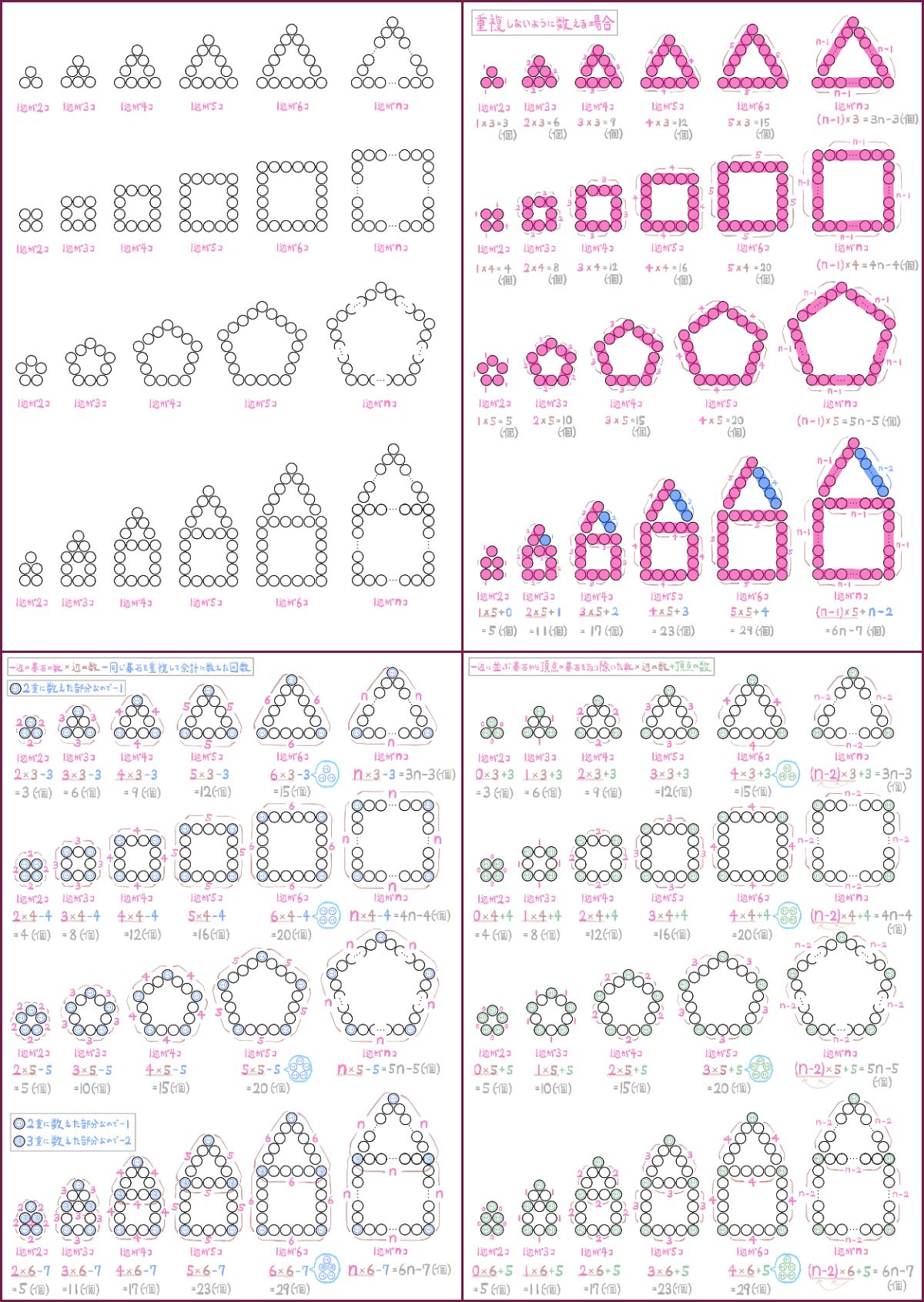
- 碁石の数がテーマの規則性の問題と碁石の数え方3通り
- 図形ごとの碁石の数の数え方|3通りまとめ
- 復習&練習用


碁石の数がテーマの規則性の問題と碁石の数え方3通り









まず、一番右から2番目の図形に書いてある式を理解しようとしてください。(左から2番目ではなく右から2番目の図形です)
それを理解する助けとして、一番右から3番目の図形や一番右から4番目の図形と式を見ます。
一番右から2番目の図形に書いてある式が理解できたら、一番右にある図形(1辺にn個の碁石が並んだ図形)の式を理解しようとしてください。
やってはいけないのは、最初に一番左にある図形の式の意味を理解しようとすることです。
その理由は、左のほうにある図形は碁石の数が少ないので「どうやってこの式になるのか」を考えても意味がわかりにくいからです。


次のように、「各辺の碁石の数から1を引いたかたまり」が何セットあるのかという考え方で、碁石の数を数えていきます。



ただし、最後の問題は「各辺の碁石の数から1を引いたかたまり」と「各辺の碁石の数から2を引いたかたまり」を作り出して、重複しないように数える必要があります。


2つ目の考え方は、重複して数えてしまった部分をあとで引こうというものです。
まず、1辺に並んだ碁石の数を数え、これが何セットあるかという計算をします。
それによって、2重にカウントしてしまった部分がありますので、その数だけマイナス1をします。
さらに、最後の問題は3重にカウントしてしまった部分も登場するので、その部分についてはマイナス2をしていきます。





最後の図形は、
2重にカウントしてしまった部分は3カ所(マイナス1が3カ所)
3重にカウントしてしまった部分は2カ所(マイナス2が2カ所)
あります。
よって、重複して数えた回数を引くために、計算の最後にマイナス7をします。

3つ目の数え方は、頂点以外の部分を最初に数えてしまって、最後に頂点の数を足すという方法です。
「1辺にならんだ碁石の数から2を引いた数」が何セットあるのかという見方をして、頂点以外の部分を数え上げていきます。
最後に、頂点の数だけ碁石を足して、計算完了となります。






図形ごとの碁石の数の数え方|3通りまとめ

碁石が3辺にn個並ぶ正三角形の場合




碁石が4辺にn個並ぶ正方形の場合




碁石が5辺にn個並ぶ正五角形の場合




碁石が6辺(家型)にn個並ぶ場合





復習&練習用















































