- 円周角の定理を使う円や半円の問題｜中学数学の定期テスト対策
中学数学の定期テスト対策の範囲です。 - 円周角の定理を使う円や半円の問題｜高校入試レベルの難問まで
三平方の定理や面積比などもからめた、高校入試で見かける問題です。
円周角の定理を使う円や半円の問題｜中学数学の定期テスト対策
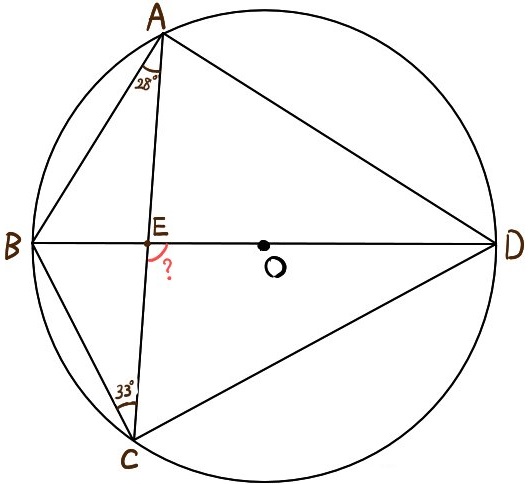
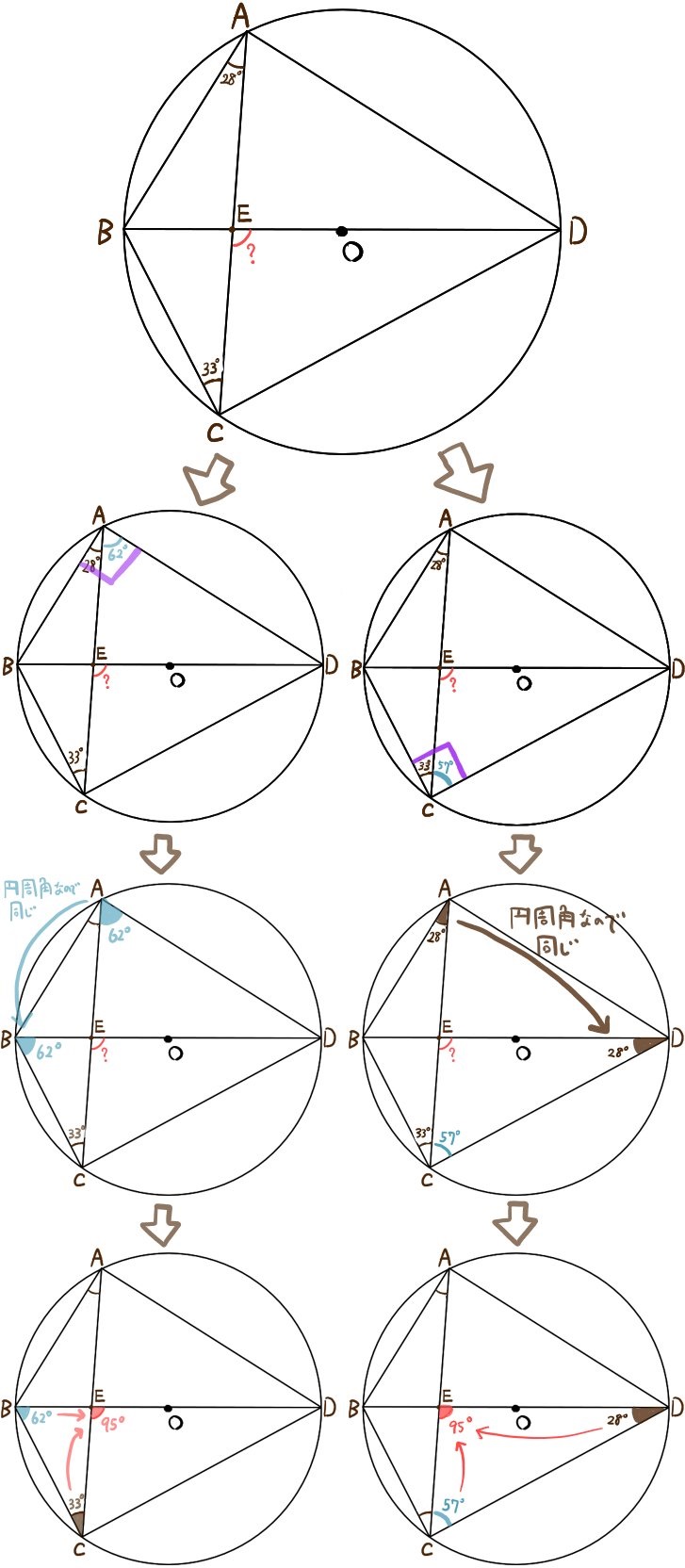
次の図のように、点Oを中心とする円に内接する四角形ABCDがある。
∠CEDの大きさを求めよ。
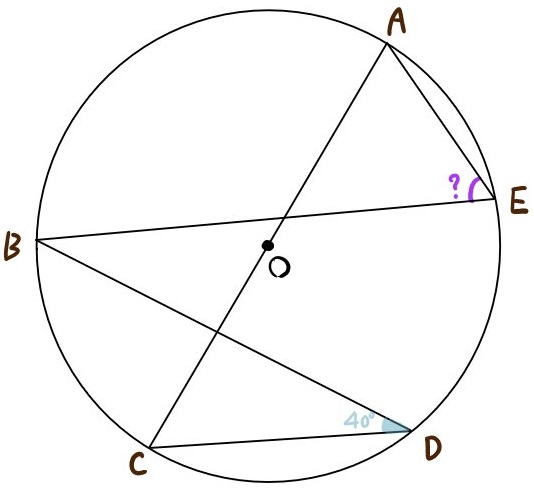
次の図のように、円周上に点A,B,C,D,Eがあり、点Oは円の中心である。
∠AEBの大きさを求めよ。
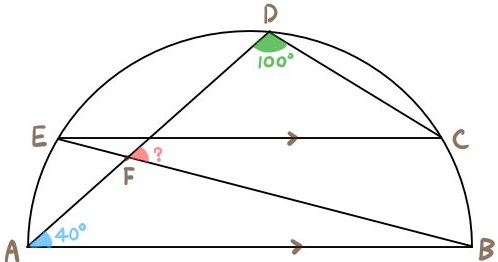
次の図のように、ABを直径とする半円がある。
∠BFDの大きさを求めよ。
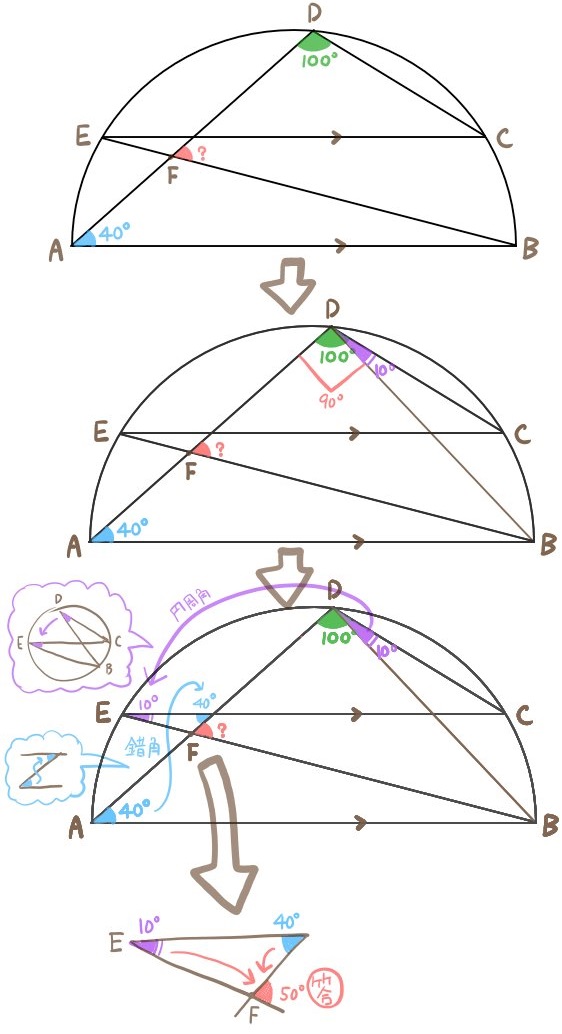１：平行線から錯角を利用する２：半円に対する円周角は直角である。
３：円周角の定理を利用する。
この３つがポイントになります。
円周上に点A、B、C、D、Eがある。
線分DBは∠CDAの二等分線
線分CEは∠DCAの二等分線
∠DAC=30°
のとき、∠EABの大きさを求めよ。
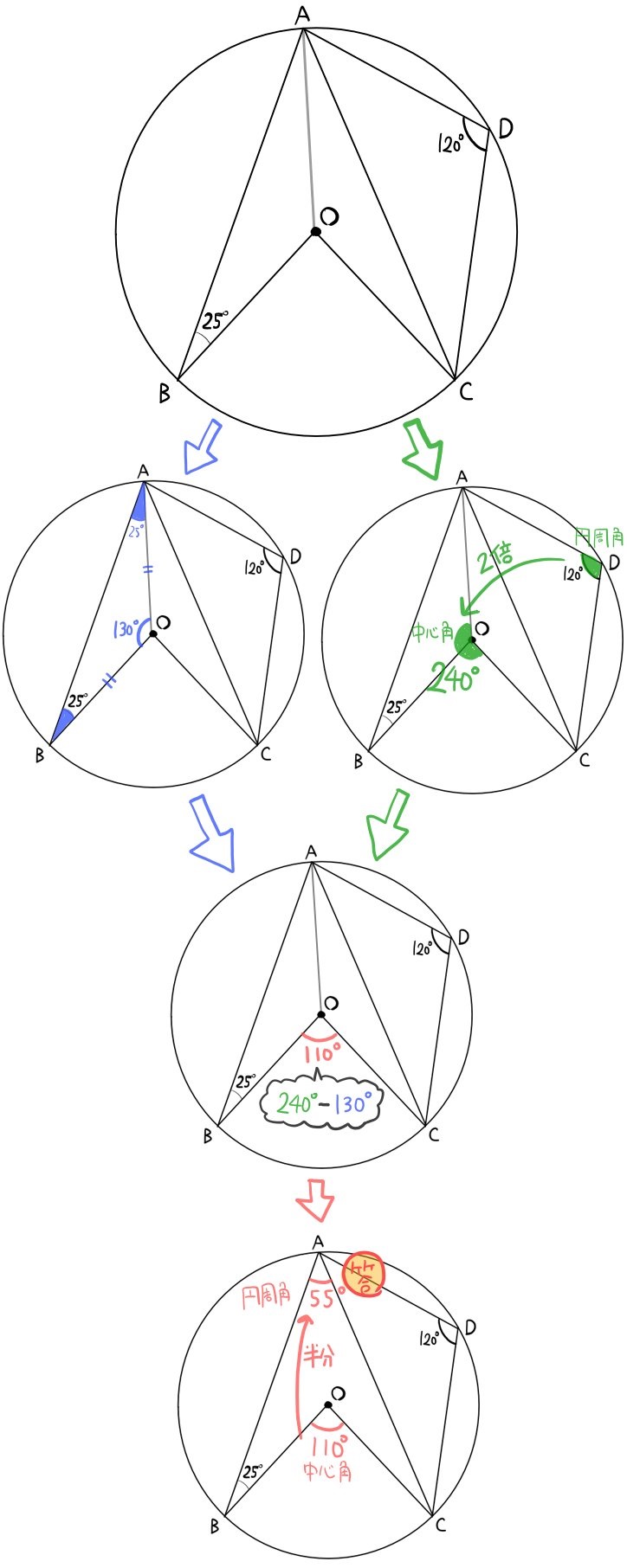
点Oを中心とする円周上に、点A、B、C、Dが次の図のようにある。
このとき、∠BACの大きさを求めよ。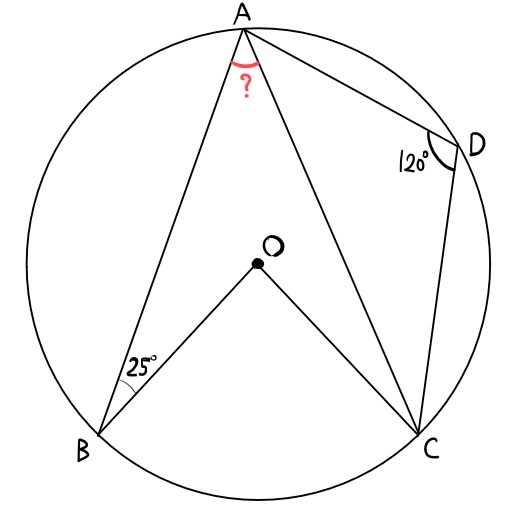
線分CDを直径とする半円があり、点Oは線分CDの中点である。
また、半円上に点A、Bがある。
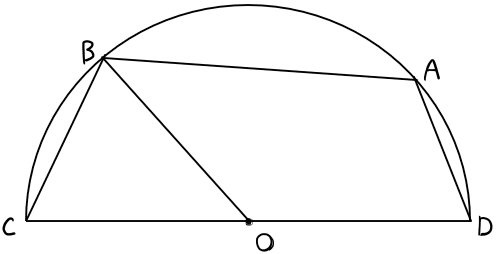
(1)∠OBC=65°のとき、∠DABの大きさを求めよ。
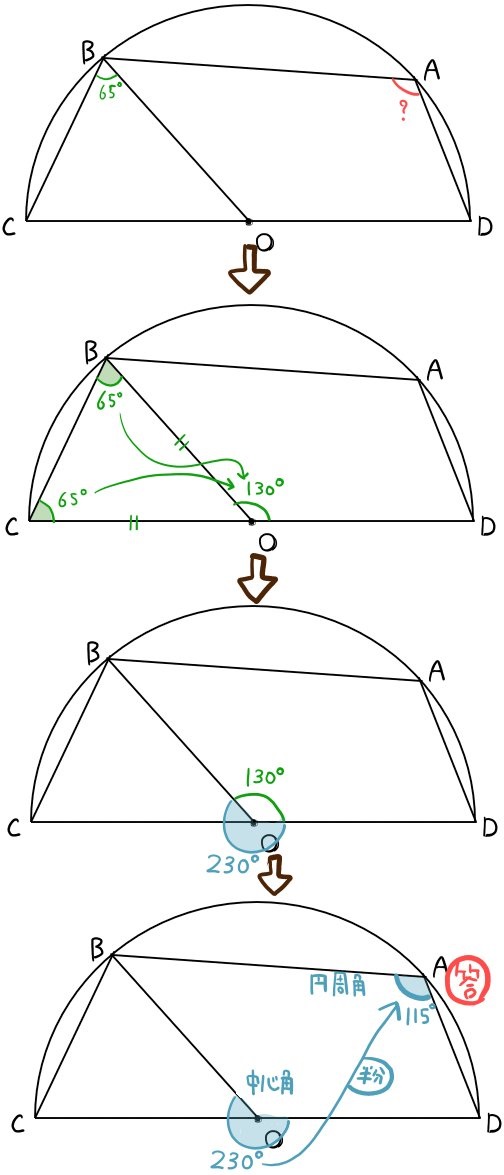
△OBCは正三角形なので、線分BCの長さは、線分OCの長さである5㎝と等しい。
よって線分BC＝5㎝
点Oを中心とする円があり、次の図のようにABとODの交点を点Cとする。
弦ABの中点を点Cとし、∠ADC=70°とする。
このとき、∠OBAの大きさを求めよ。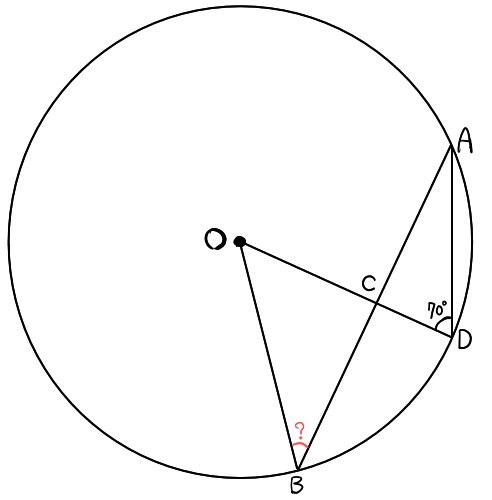
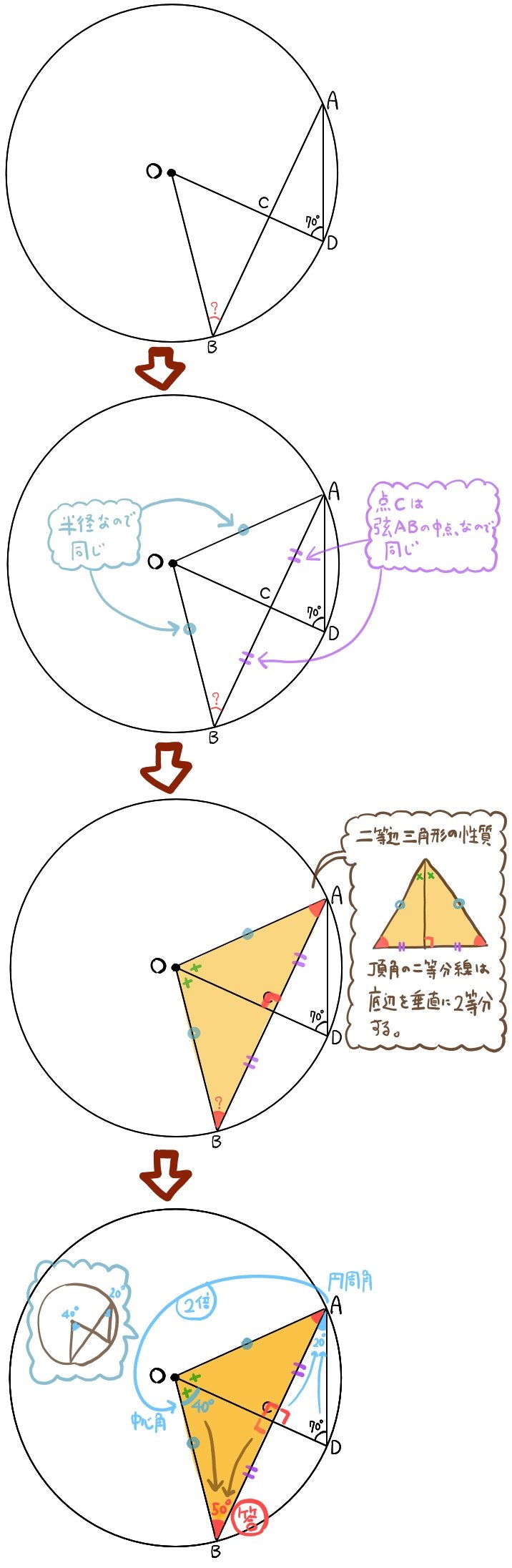二等辺三角形の性質を思い出し、それを利用するところが、慣れていないと難しいでしょう。また、最後に円周角を倍にした大きさである中心角の値を求めていますが、意識しないと気が付きにくいポイントです。
円の半径はどの線も長さが等しく、そこからできる二等辺三角形の性質を利用する問題です。
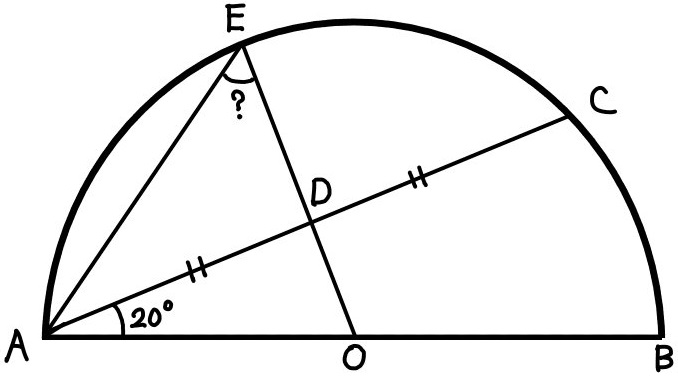
ABを直径とする半円がある。
点OはABの中点である。点DはACの中点である。∠BAC＝20°である。
∠OEAの大きさを求めよ。（島根県）
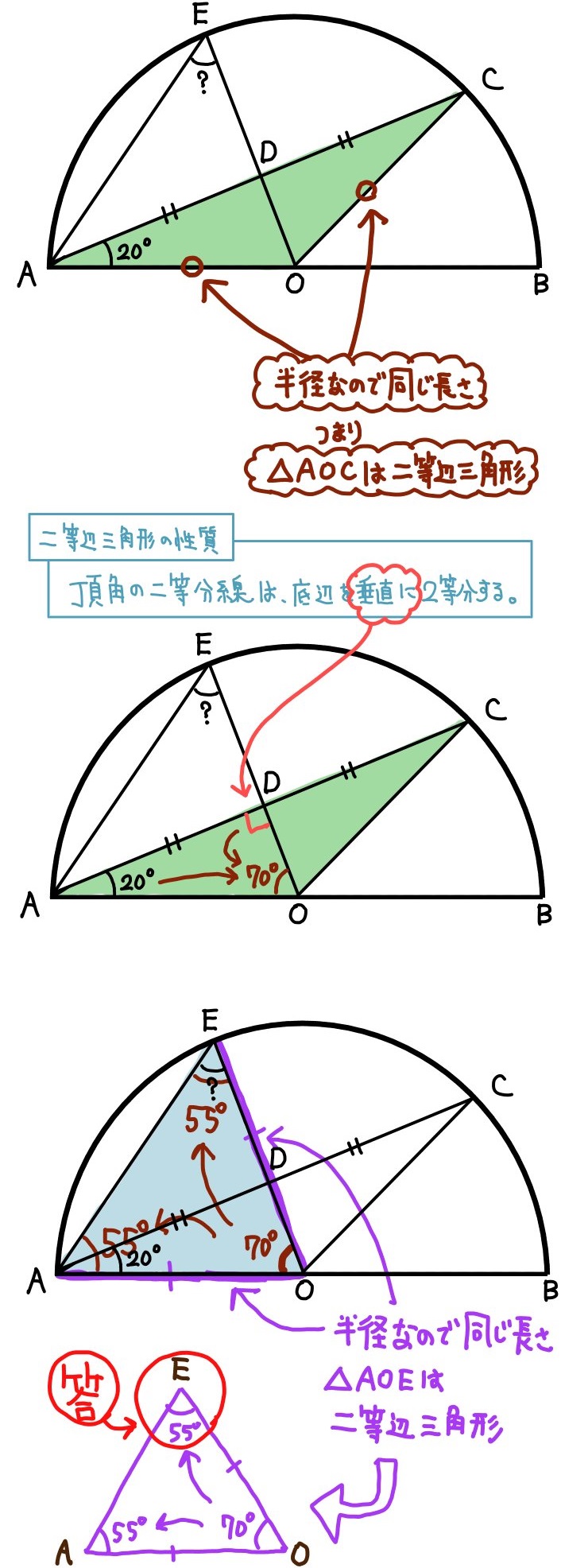
中点連結定理を利用できる図形である、ということに気が付くと糸口が見つかります。
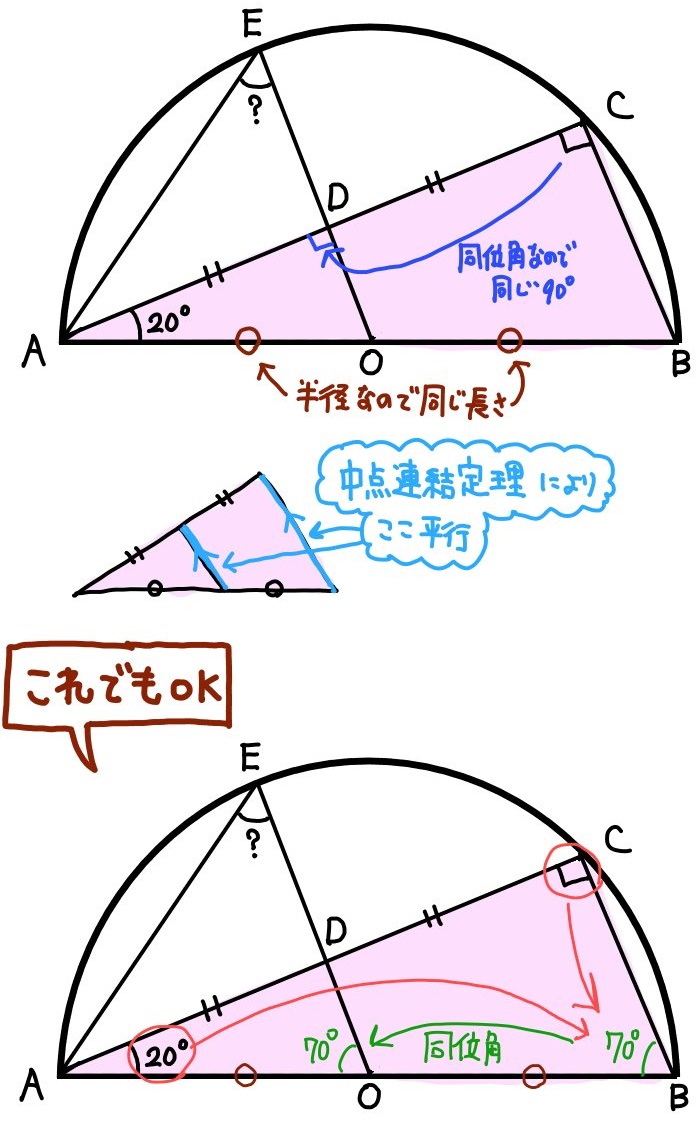あとは、最初の解法の通りに進めばOkです。
別解に示したように、中点連結定理を利用する解法の２通りで解ける状態にしておきましょう。
円周角の定理を使う円や半円の問題｜高校入試レベルの難問まで
次の図において、点Oは円の中心である。
AB=AC
∠ABC=30°
である。
(1)∠BOCの大きさを求めよ。
このかたちは、どちら側の中心角の大きさが、円周角の２倍になっているのか、わかりにくい方も多いと思いますので、慣れておきましょう。
次の図において、点Oは円の中心であり
\(AB=9\) ㎝
\(BC=8\) ㎝
\(CA=7\) ㎝
線分ADは線分BCの垂線である。(早稲田実業高校)
(1)線分ADの長さを求めよ。
(2)円の直径AEの長さを求めよ。
どの円周角とどの円周角が等しいのか気が付くのが難しい問題です。
半径がa(㎝)の円の中心とoとし、また円周上に点A,B,C,D,Eが以下のようにある。
このとき、赤色の部分の面積をaを使って表せ。
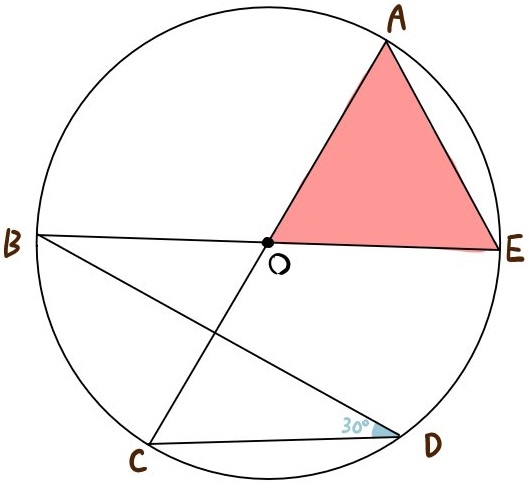
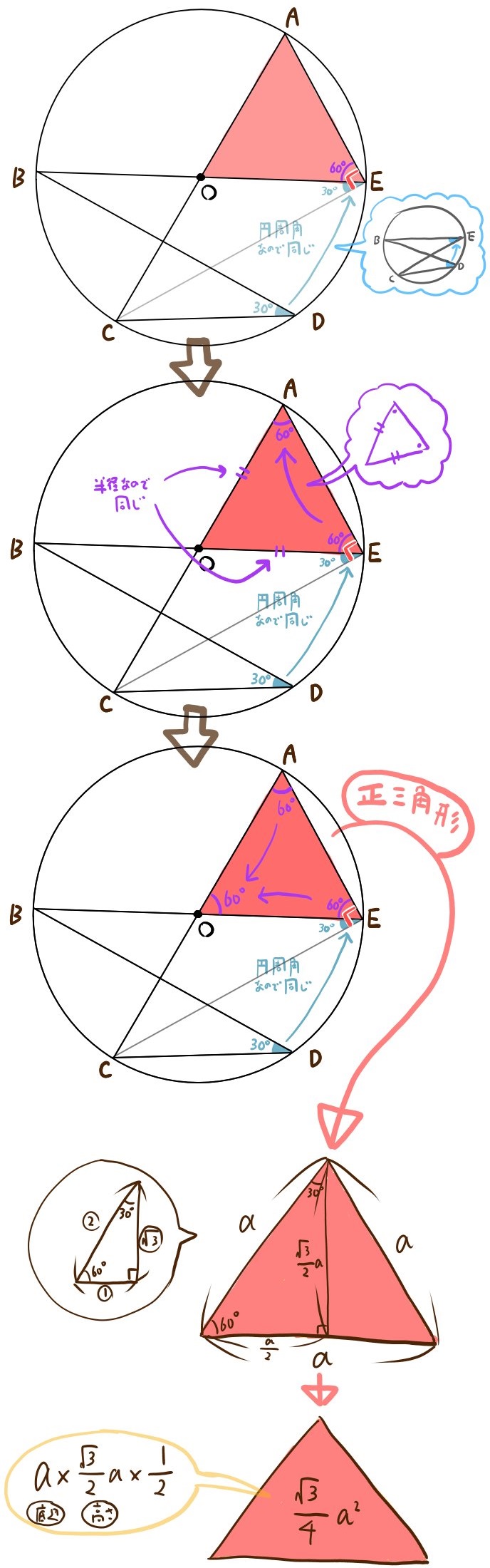
円の直径がある問題の場合、円周定理により90°となる角度を利用する場合が多いです。そのような思考で、まず補助線を引いてみるクセを付けるといいでしょう。
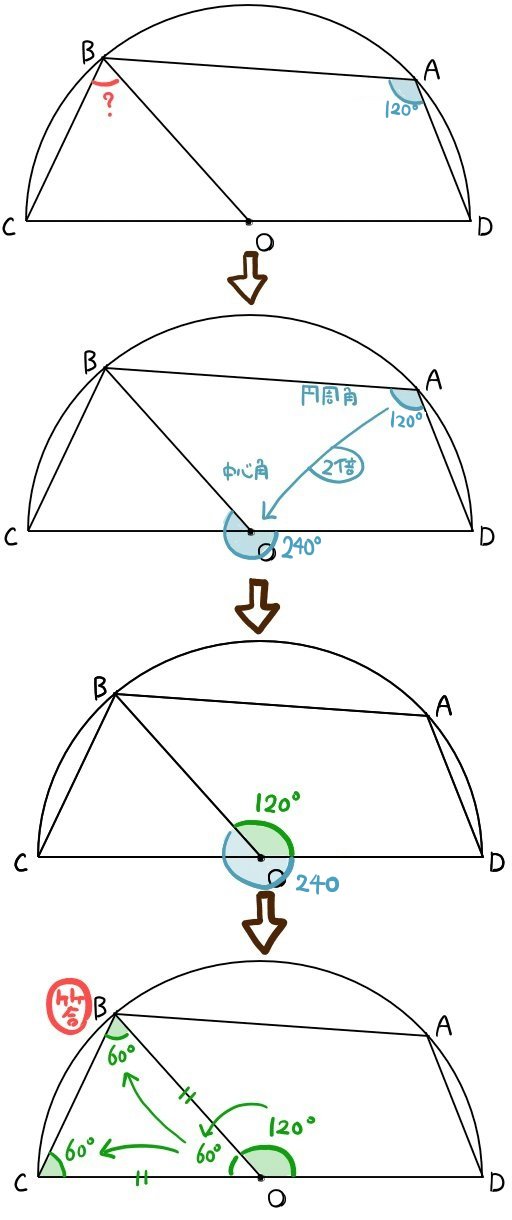
次の図において、点Oは半径1の円の中心である。
また、∠ADC=120°である。
線分ABの長さを求めよ。
円の直径を両端とする弧に対する円周角（半円に対する円周角）は90°です。これを利用すべく補助線を引きます。円に内接する四角形の問題のように見えますが、これも先程と同じ補助線の引き方をすることで、よく知った問題だということが見えてきます。
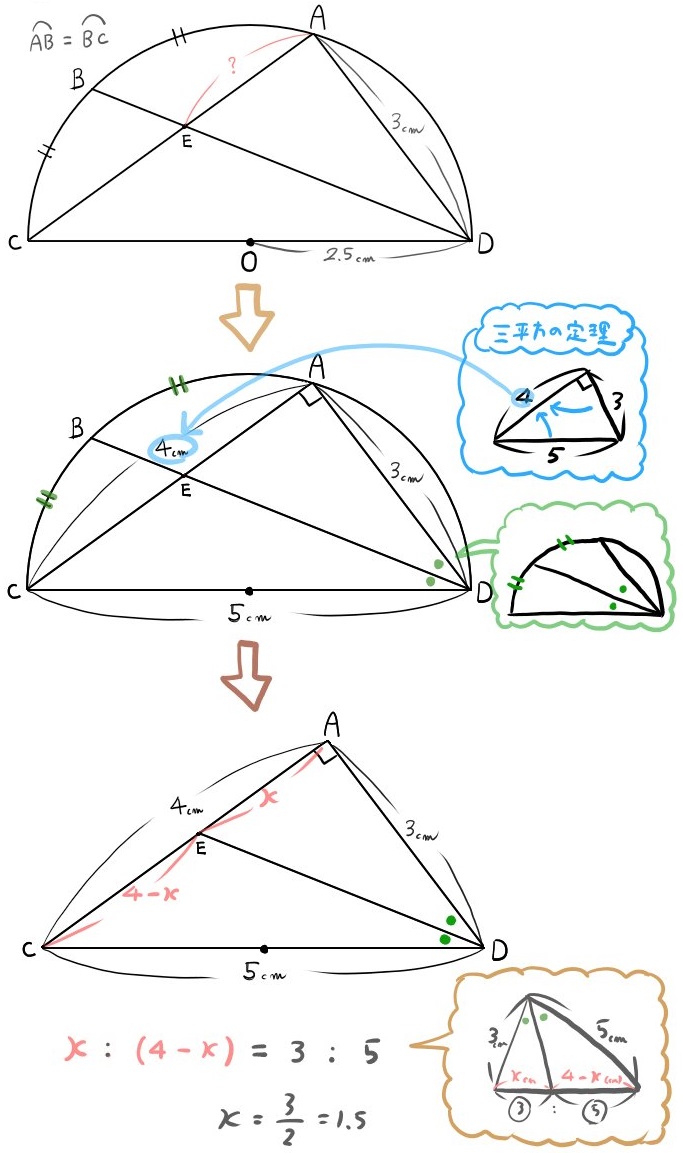
線分CDを直径とする半円があり、点A、B、C、D、Eが次の図のようにある。
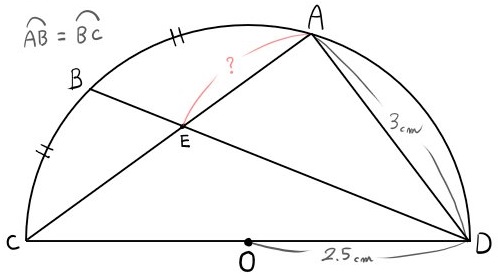
弧ABと弧BCの長さが等しく、AD=3㎝、OD=2.5㎝である。
このとき、線分AEの長さを求めよ。
線分ABを直径とする半円があり、ABの中点をOとする。
OB=BC=6㎝である。
赤い部分の面積を求めよ。
このような問題の場合は、扇形の面積をとして求めるとしたら、どの部分のことだろうか？と考えてみます。中学数学では、曲線が含まれる図形の面積と言えば、円や半円や扇形の面積しか求め方を学習しないので、それらの組み合わせで問題が作られています。よって、そのような考え方を巡らせると有効です。
次の図において、∠EFDの大きさと∠DCEの大きさをそれぞれ求めよ。
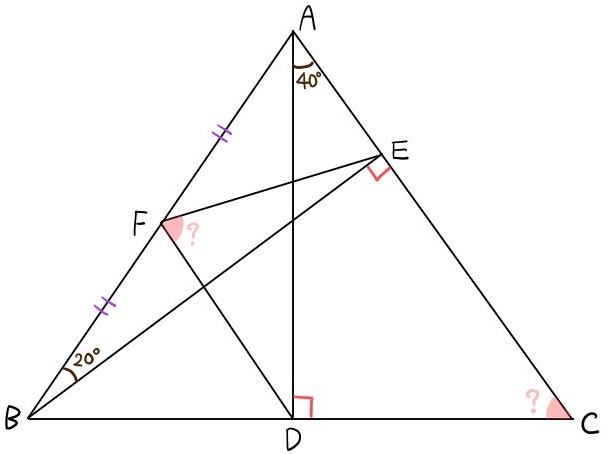
円周角の定理の逆より、次の図のように円に内接する三角形としてとらえることができます。
円周角の定理の逆を利用して、円に内接する図形を見出します。その練習になる問題です。
点Oを中心とする半径3㎝の円がある。この円周上に、次の図のように各点がある。
BC=3㎝
CD=4㎝
BD⊥CEである。
(1)△BCEと△ACDの面積比を、最も簡単な整数の比で表せ。
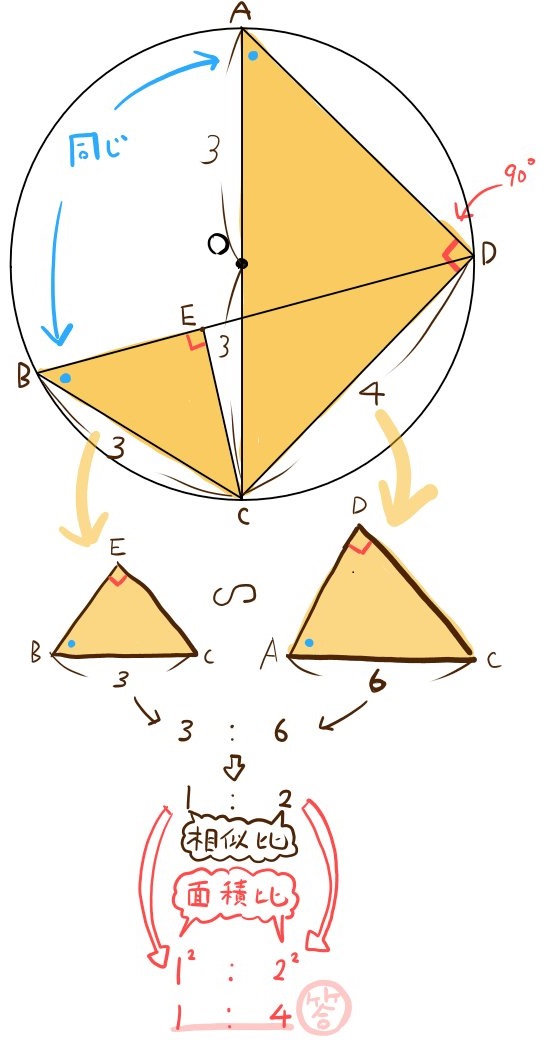
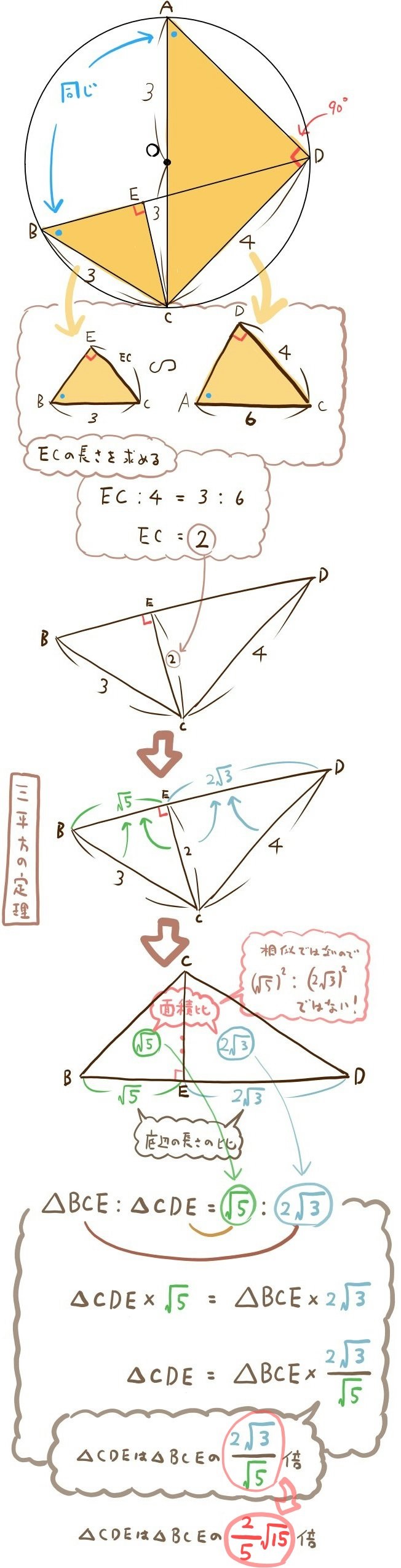
(2)△CDEの面積は△BCEの面積の何倍か。
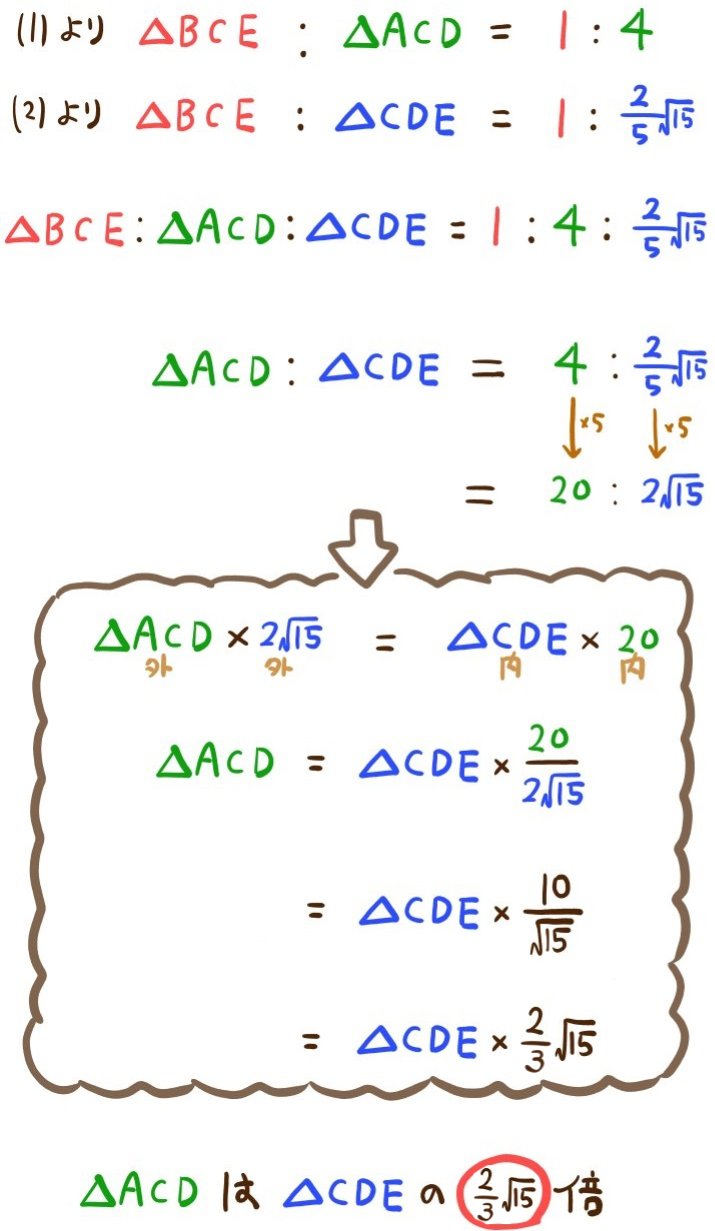
(3)△ACDの面積は△CDEの面積の何倍か。
次の図において(1)～(4)の問いに答えよ。
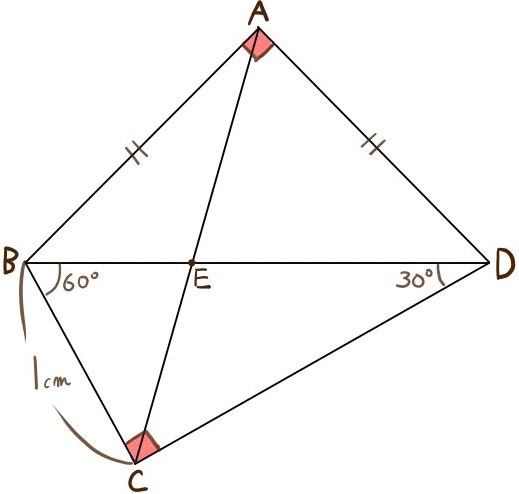
(1)四角形ABCDの面積を求めよ。
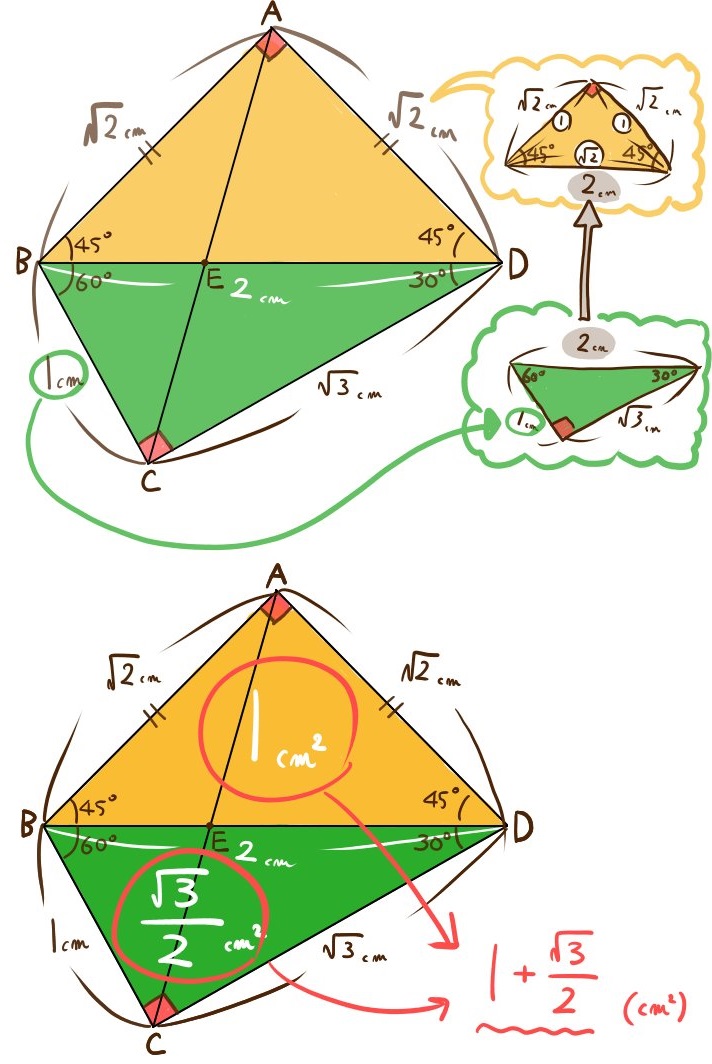
(2)△ABEと△DCEの面積比を最も簡単な整数の比で表せ。
また、△BCEと△ADEの面積比を最も簡単な整数の比で表せ。
（△BCEと△ADEの面積比は）１：２
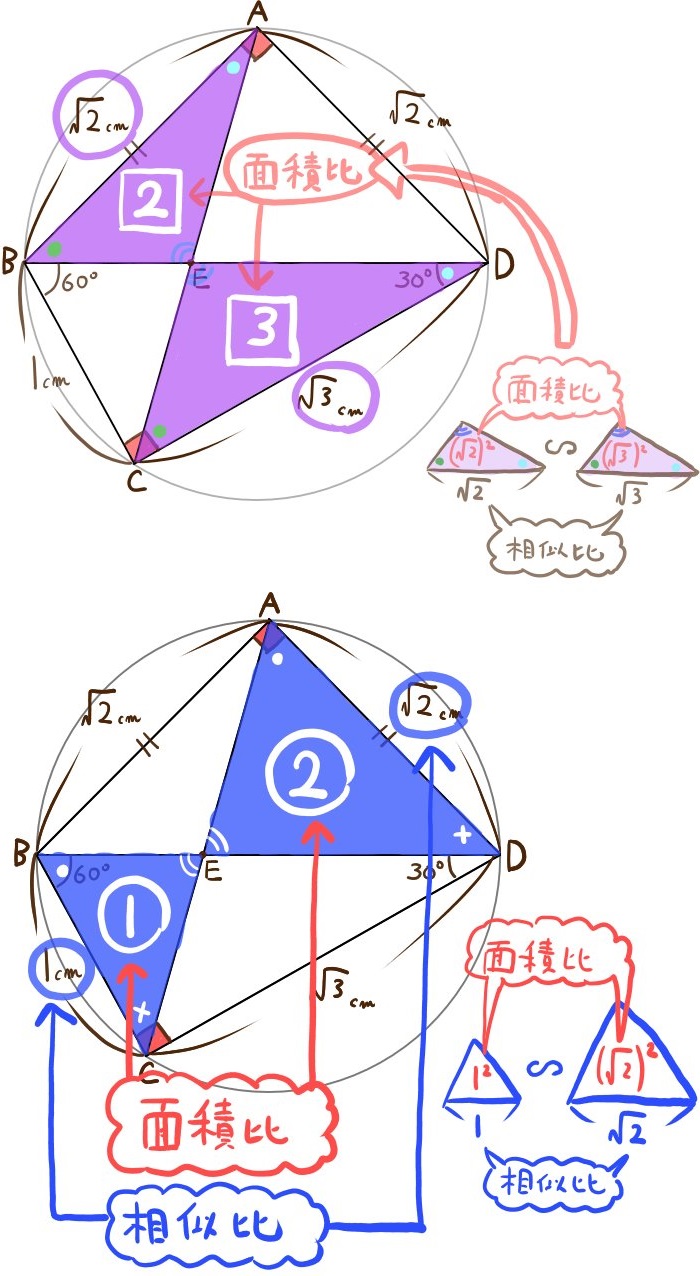
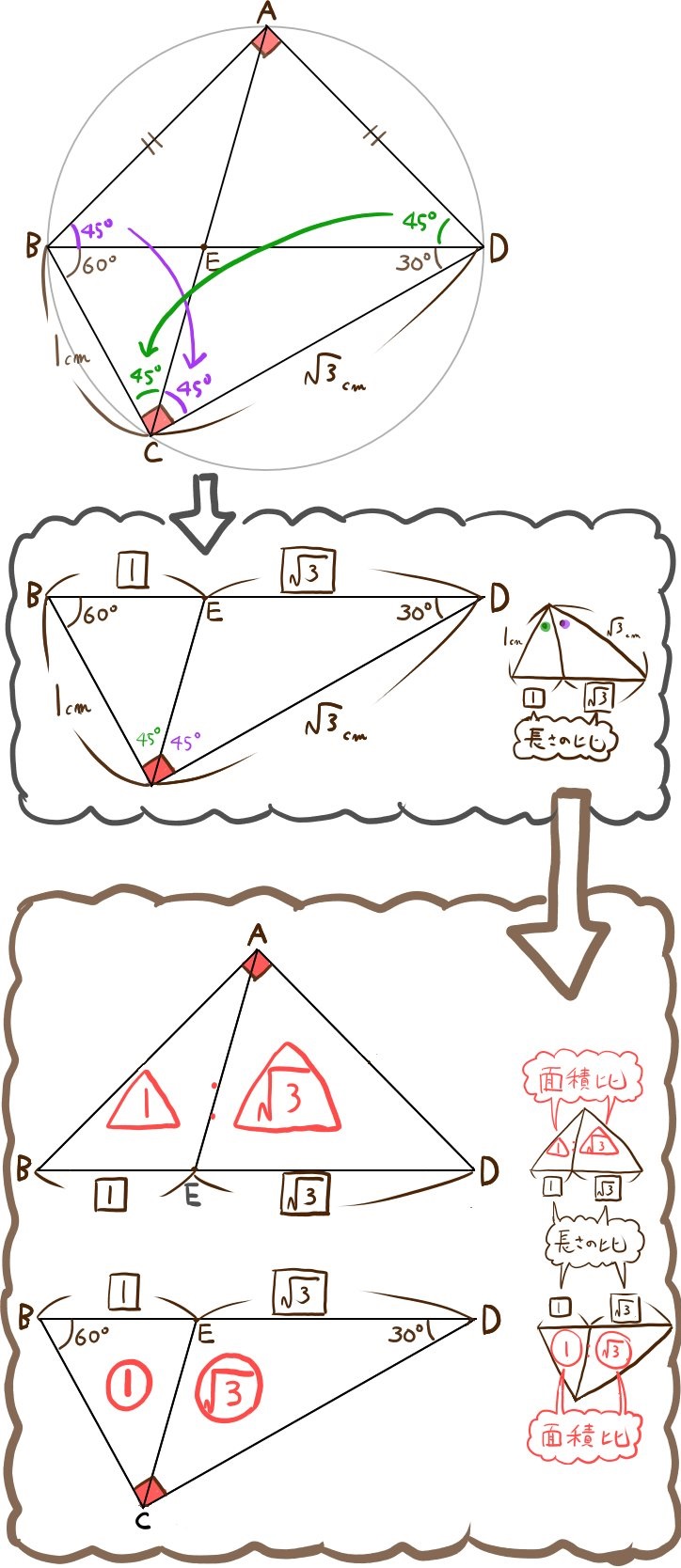
(3)△ABEと△ADEの面積比を表せ。
また、△BCEと△DCEの面積比を表せ。
（△BCEと△DCEの面積比は）１：\(\sqrt{3}\)
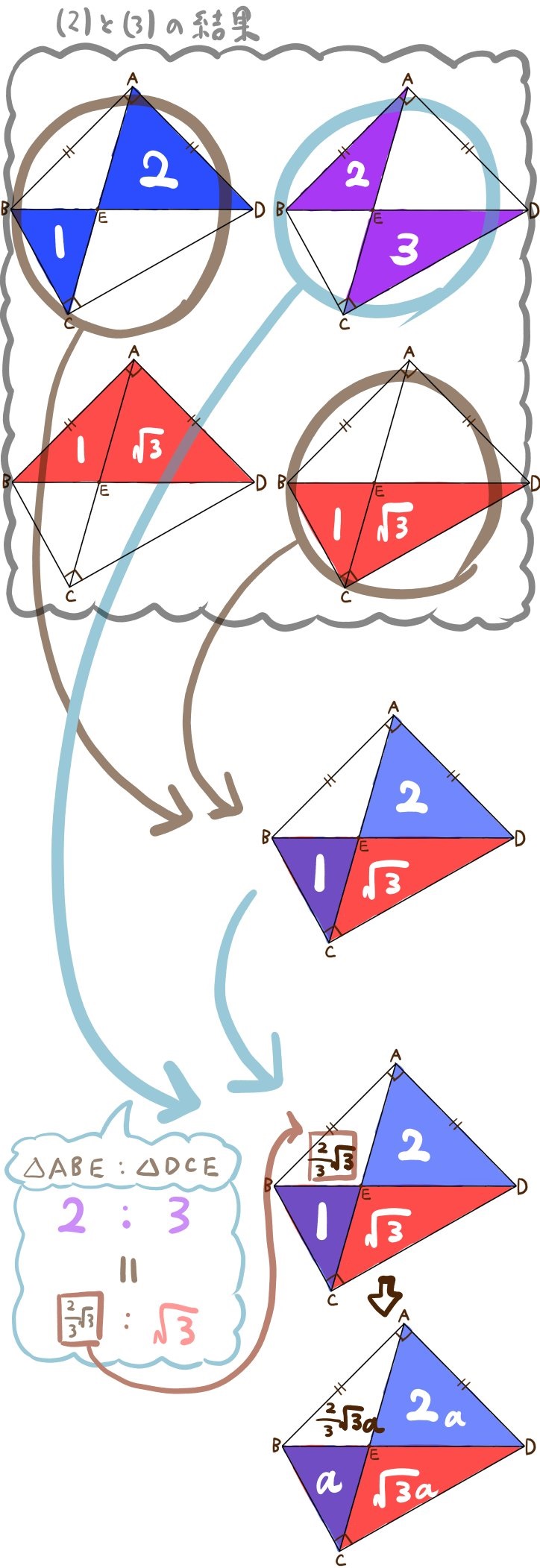
(4)△BCEの面積をaとする。このとき
△ABE、△ADE、△DCEの面積について、それぞれaを使って表せ。
△ABEの面積は \(\dfrac{2}{3}\sqrt{3}\)
△ADEの面積は2a
△DCEの面積は \(\sqrt{3}a\)
下の図において、点Mは線分ACの中点である。
∠CBA=90°
∠CDB=90°
BC= \(\sqrt{3}\) (㎝)
AB= \(\sqrt{5}\) (㎝)
である。
(明訓高校)
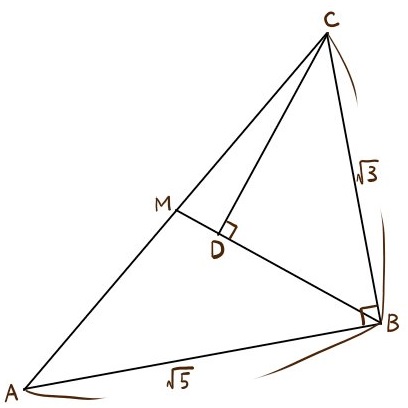
(1)ACの長さを求めよ。
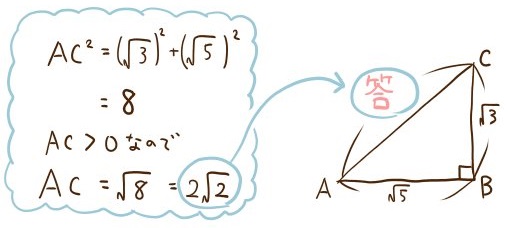
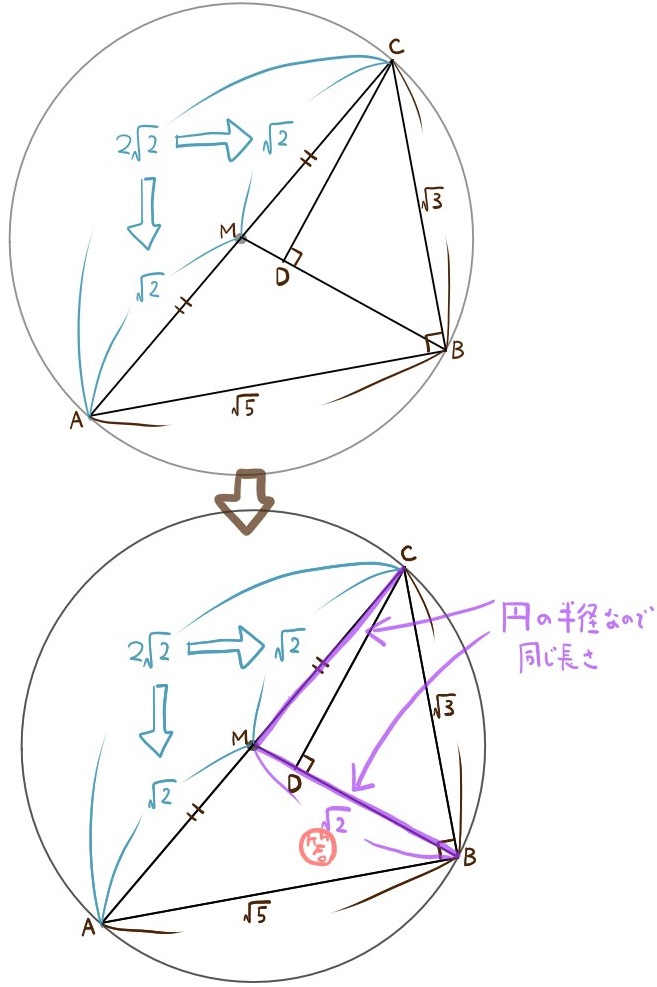
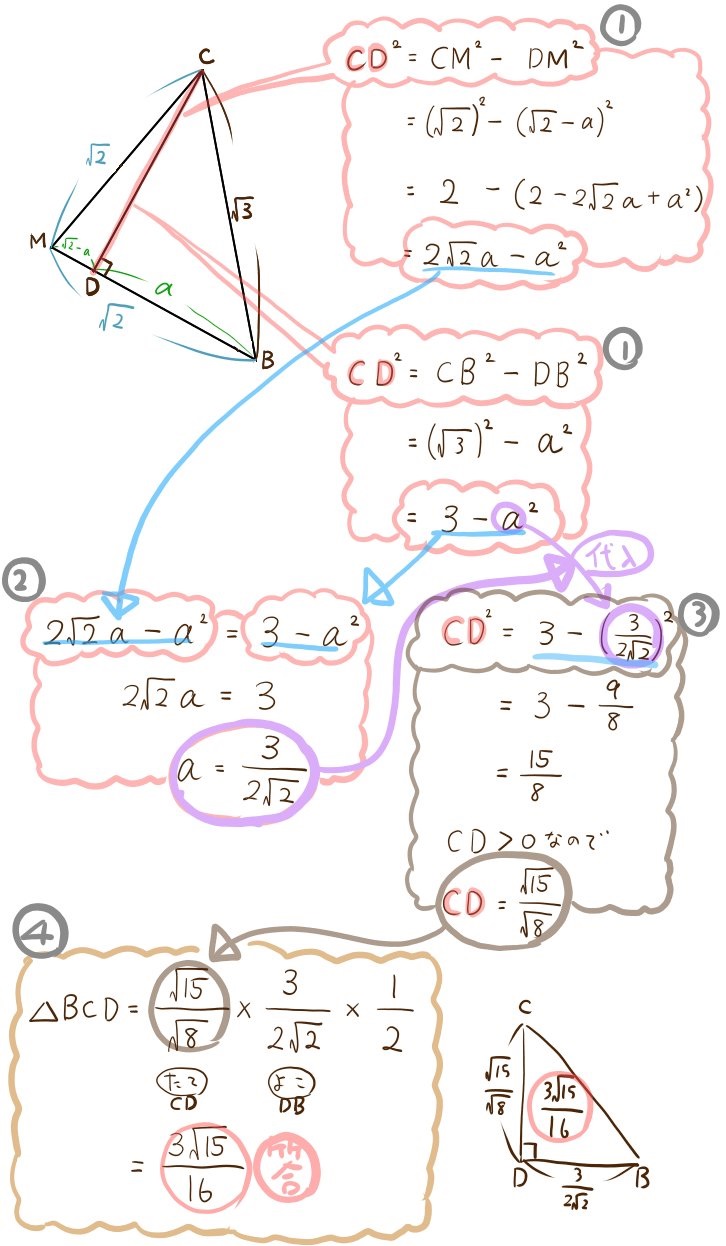
(3)△BCDの面積を求めよ。
線分ABを直径とする半円がある。
\(AB=4\sqrt{5}\) ㎝
\(AD=4\) ㎝
△ADB∽△EDAである。(明訓高校)
(1)BDの長さを求めよ。
よって \(BD=8\) ㎝
（△EDAと△ABEの面積の比は）1:3
（△ABEの面積は）12㎠
(3)△ECBの面積は△EDAの面積の何倍か？
線分ABを直径とする半円がある。
弧ADと弧CDの長さが等しい。
AB=10(㎝)
AD=6(㎝)
線分ACと線分BDとの交点をEとする。(熊本県:改)
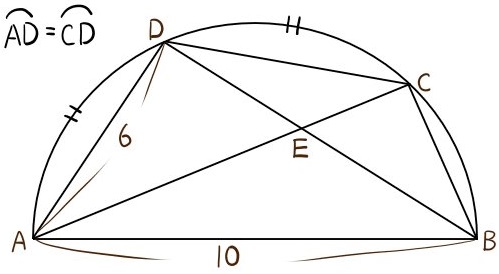
(1)△ABEと△DBCの面積比を求めよ。
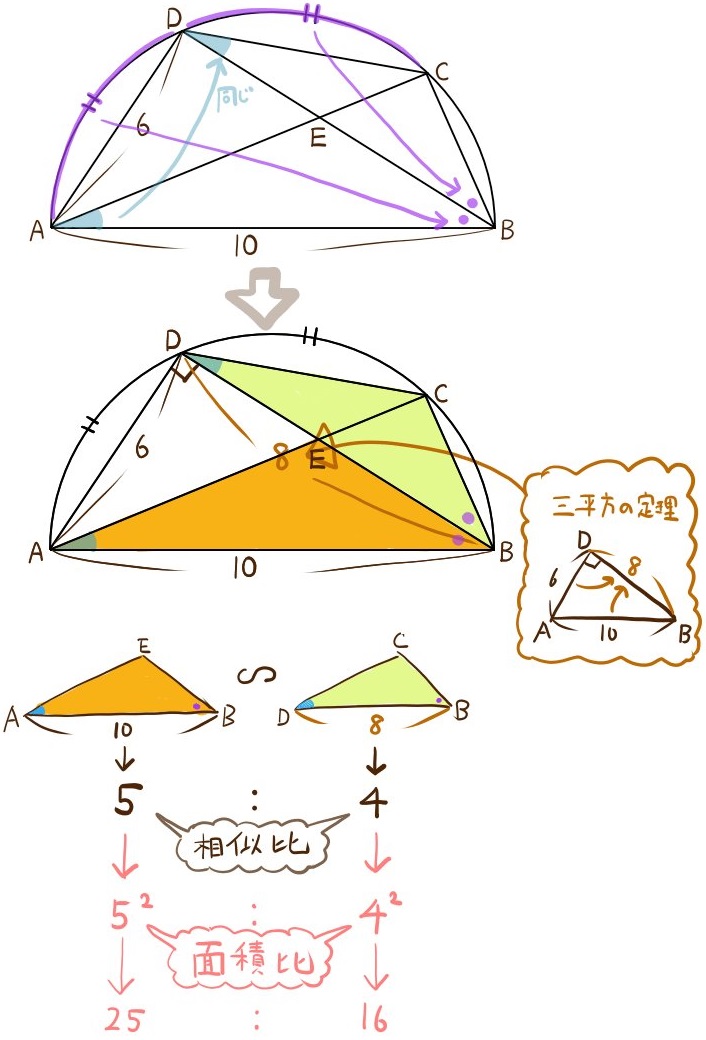
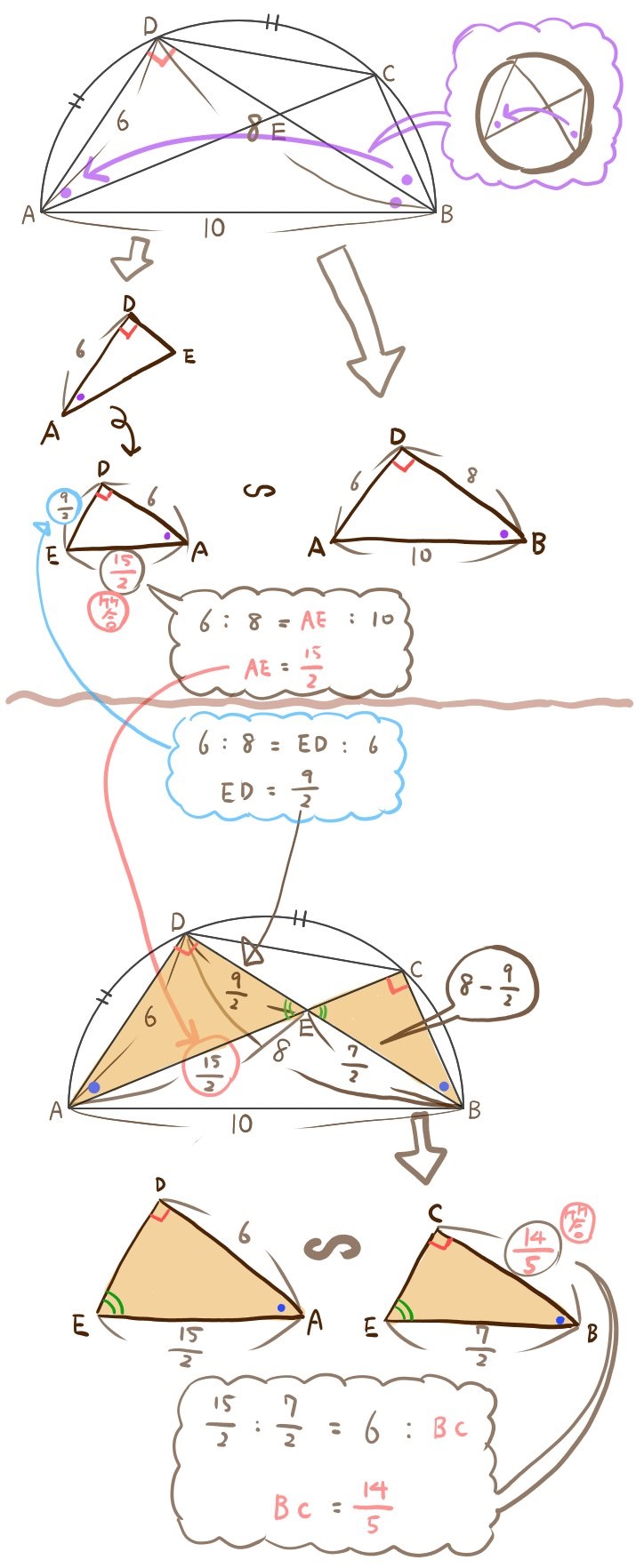
弧の長さが等しい問題の場合は、その弧から成す円周角の大きさは等しいので、まずそのことを書き込んで、考える材料としましょう。
