
このページの内容
- 定数項の大きい因数分解の解き方
- 定数項や係数の大きい因数分解の練習問題
- このパターンの因数分解を解く力をもっと鍛えたい方へ

にゃんこ
高校入試で出題される因数分解のなかに、定数項の大きい場合があります。

坂田先生
例えばこのような問題です。

坂田先生
ここでは、このような定数項の大きい因数分解の解き方とコツを解説し、さらにこのパターンの対策となる練習問題を用意しています。
定数項の大きい因数分解の解き方

坂田先生
先程の問題を例に、解き方を解説します。
因数分解しなさい。
\(x^{2}y-xy-156y\)
\(x^{2}y-xy-156y\)

にゃんこ
解き方はこうです。(まずはザッとご覧ください)
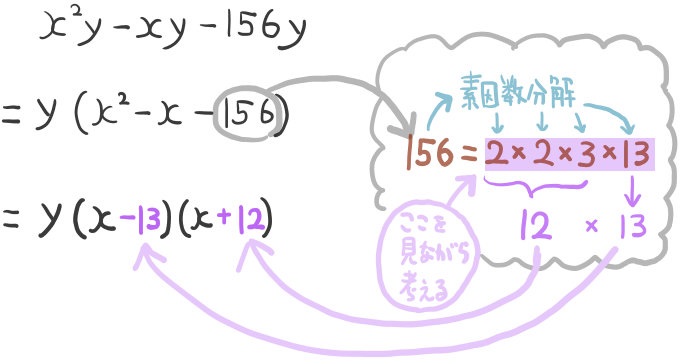
定数項の値が多い場合、このように、定数項を素因数分解します。
並んだ素因数をながめながら、(この問題の場合は)差が1になるような因数の組み合わせを探します。
その結果、解答にある通り、12と13の組み合わせが見つかったというワケです。
よって、積が-156になり和が-1になる数の組み合わせは、-13と12ということになります。
和が-1になる数の組み合わせから考えると無限に組合せが考えられますので、和から考えることはおすすめしません。

坂田先生
以上をまとめるとこうなります。
係数や定数項が大きい場合の因数分解の解き方手順
- 定数項を素因数分解する
- その素因数分解されたかたちを眺めながら、2つの数の組み合わせを探す
- 因数分解完了

にゃんこ
次に、この解法をマスターするための練習をしてみましょう。
定数項や係数の大きい因数分解の練習問題
(1) \(x^{2}+3x-700\)
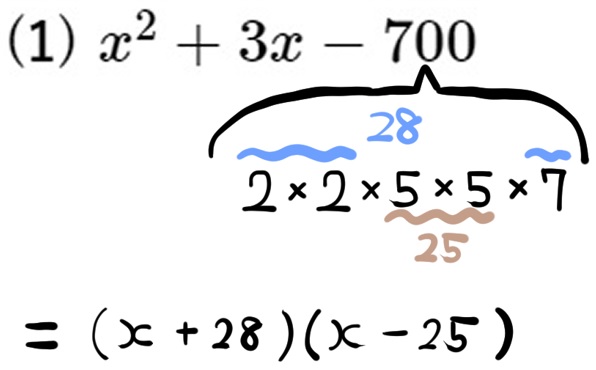 ~積が-700になり、和が3になる2数を突き止める流れ~
~積が-700になり、和が3になる2数を突き止める流れ~
定数項が負の数なので、2数は「正の数×負の数」または「負の数×正の数」というように異符号になります。
その異符号の2数の和が3になるということは、符号を無視した数だけの部分を見ると、その差が3になる組み合わせを探せばいいということになります。
素因数分解された定数項2×2×5×5×7の並びをみると、28と25の組み合わせの差が3になるので、これだということがわかります。
さいごに2数が異符号だという条件により、28と-25であればよいと突き止めることができました。
これで因数分解をします。
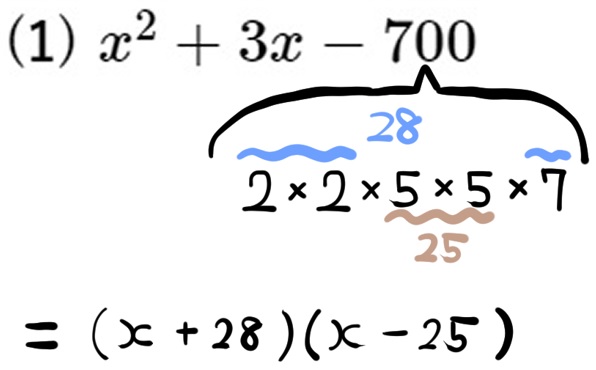
定数項が負の数なので、2数は「正の数×負の数」または「負の数×正の数」というように異符号になります。
その異符号の2数の和が3になるということは、符号を無視した数だけの部分を見ると、その差が3になる組み合わせを探せばいいということになります。
素因数分解された定数項2×2×5×5×7の並びをみると、28と25の組み合わせの差が3になるので、これだということがわかります。
さいごに2数が異符号だという条件により、28と-25であればよいと突き止めることができました。
これで因数分解をします。
(2) \(x^{2}-55x+700\)
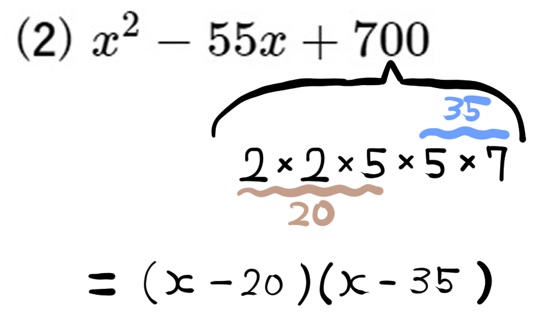
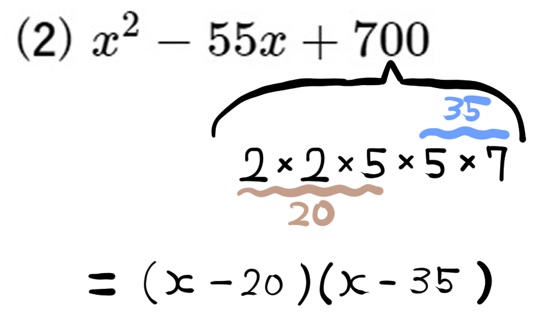
(3) \(x^{2}+9x-910\)
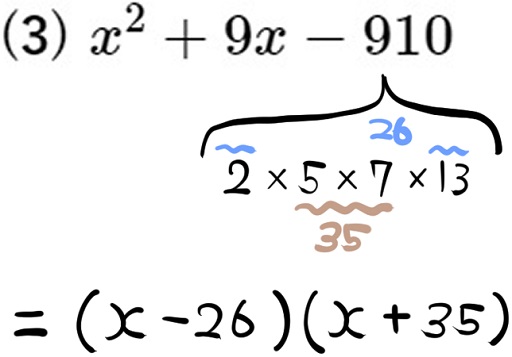 ~積が-910になり、和が9になる2数を突き止める流れ~
~積が-910になり、和が9になる2数を突き止める流れ~
先程と同じように定数項が負の数なので、2数は異符号になります。
その異符号の2数の和が9になるということは、符号を無視した数だけの部分を見ると、その差が9になる組み合わせを探せばいいということになります。
定数項2×5×7×13の並びから、26と35の組み合わせの差が9になるので、-26と35(2数は異符号)だと判明します。
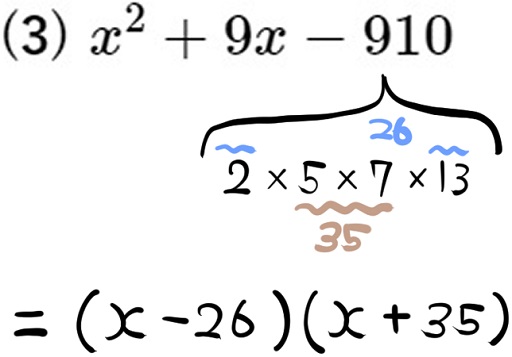
先程と同じように定数項が負の数なので、2数は異符号になります。
その異符号の2数の和が9になるということは、符号を無視した数だけの部分を見ると、その差が9になる組み合わせを探せばいいということになります。
定数項2×5×7×13の並びから、26と35の組み合わせの差が9になるので、-26と35(2数は異符号)だと判明します。
(4) \(x^{2}+83x+910\)
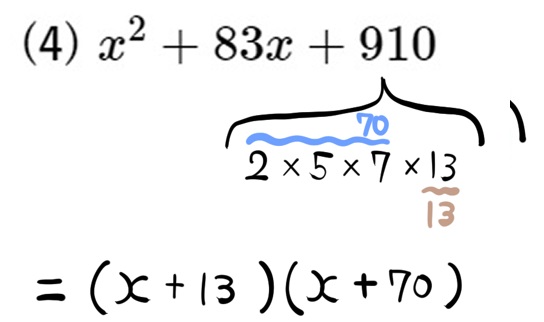
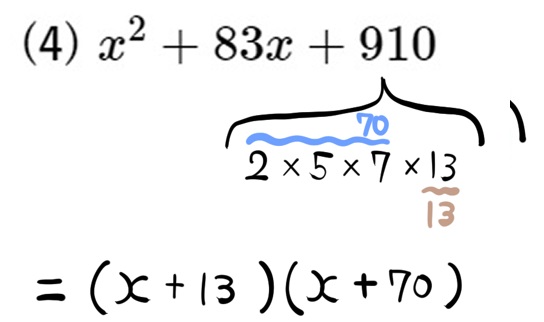
(5) \(x^{2}+77x+1210\)
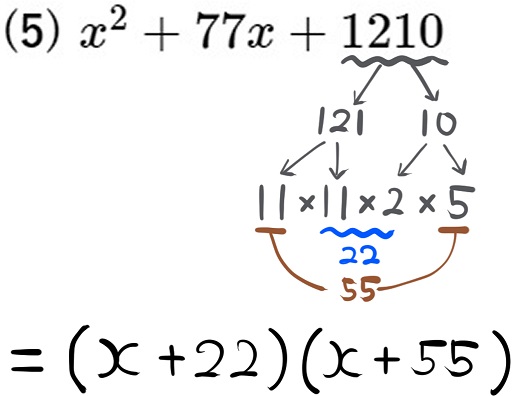 ~ちょっとしたテクニック~
~ちょっとしたテクニック~
定数項の素因数分解ですが、この問題のように、10の倍数があれば、121と10というように分解すると、処理が楽に進められます。
一つひとつ素因数で割る方法だと時間がかかることが多いので、大きな数はこの方法で素因数分解することを個人的にはおすすめします。
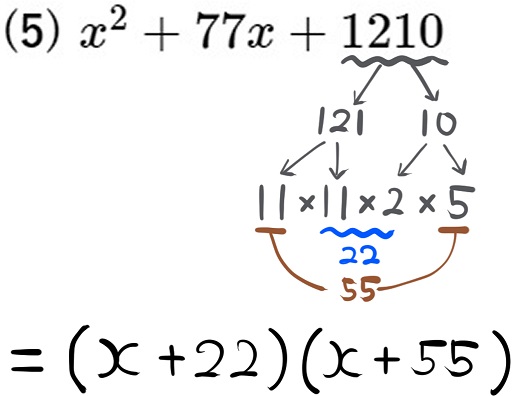
定数項の素因数分解ですが、この問題のように、10の倍数があれば、121と10というように分解すると、処理が楽に進められます。
一つひとつ素因数で割る方法だと時間がかかることが多いので、大きな数はこの方法で素因数分解することを個人的にはおすすめします。
(6) \(x^{2}+99x-1210\)
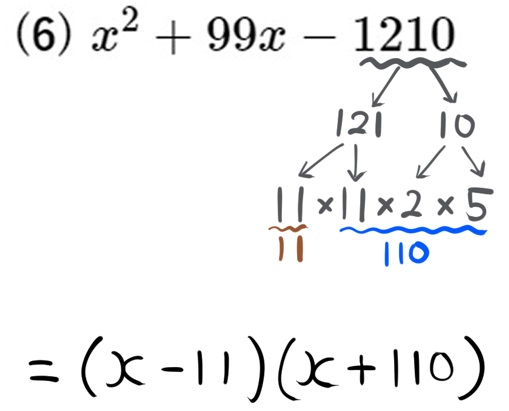
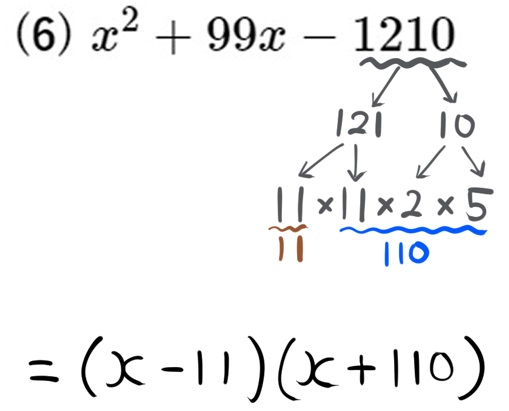
(7) \(x^{2}+54x+3^{4}\times 5\)
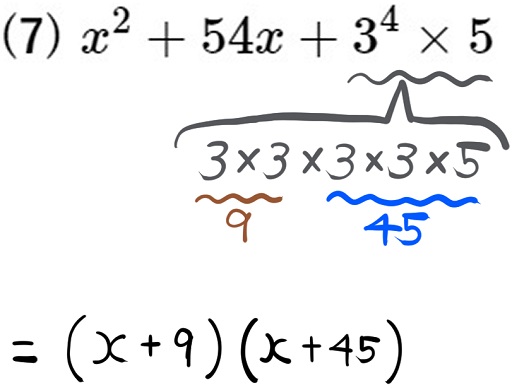 積が \(3^{4}\times 5\) になり、和が54になる2数の探し方
積が \(3^{4}\times 5\) になり、和が54になる2数の探し方
定数項が正の数なので、2数は「正の数×正の数」または「負の数×負の数」というように同符号になります。
その同符号の和が54になればいいので、定数項3×3×3×3×5の並びから探し、9と45であれば良いと気が付きます。
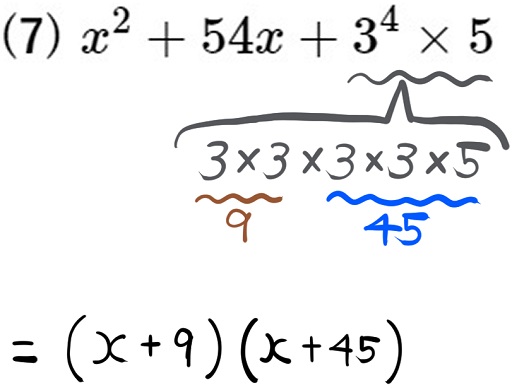
定数項が正の数なので、2数は「正の数×正の数」または「負の数×負の数」というように同符号になります。
その同符号の和が54になればいいので、定数項3×3×3×3×5の並びから探し、9と45であれば良いと気が付きます。
(8) \(x^{2}+138x+3^{4}\times 5\)
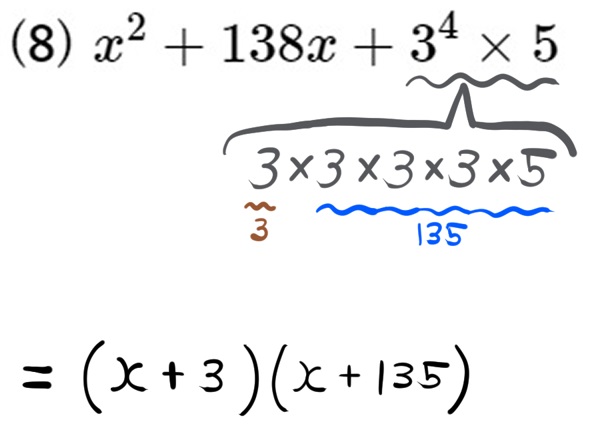
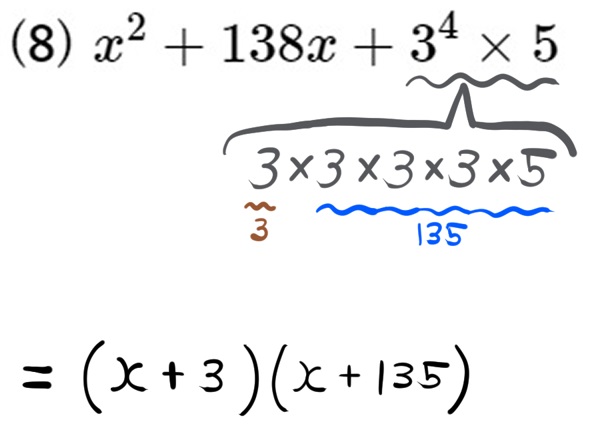
(9) \(420a-ab\left( 82-2b\right) \)
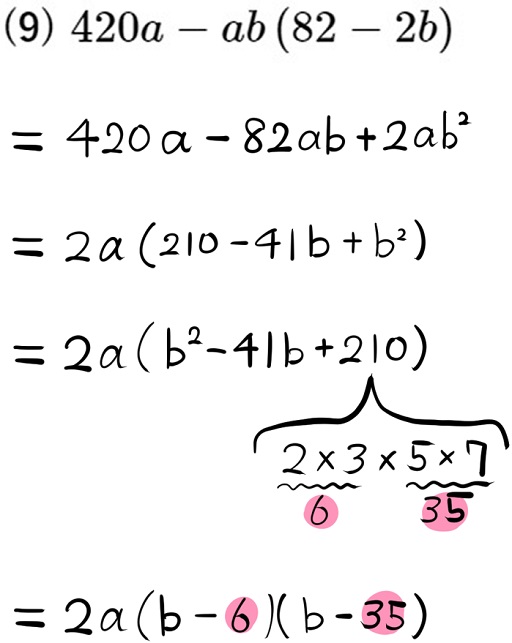 最初の変形が少しややこしいですが、それが済むと、このページで学習している問題と同じパターンになります。
最初の変形が少しややこしいですが、それが済むと、このページで学習している問題と同じパターンになります。
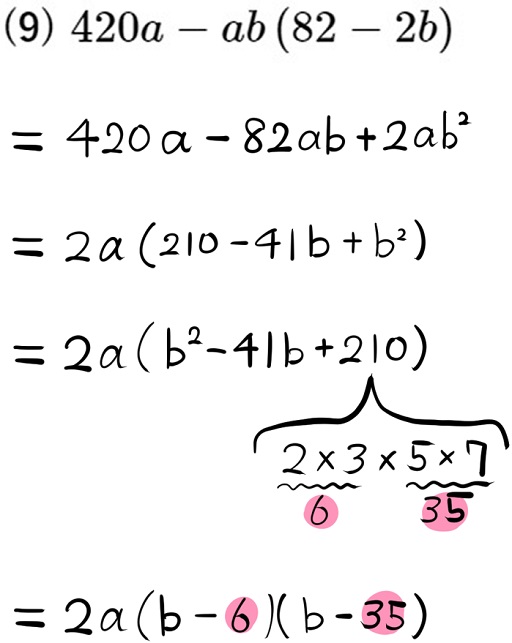
(11) \(x^{2}+36\times 7x+2^{7}\times 7^{2}\)
 このテーマの難問です。
このテーマの難問です。
xの係数が7の倍数なので、36×7は、7の倍数同士の和になるという予測ができます。
なので、積が \(2^{7}\times 7^{2}\) 和が \(36×7\) になる2数の組み合わせは、〇×7と□×7のかたちになっていると予測がつきます。

xの係数が7の倍数なので、36×7は、7の倍数同士の和になるという予測ができます。
なので、積が \(2^{7}\times 7^{2}\) 和が \(36×7\) になる2数の組み合わせは、〇×7と□×7のかたちになっていると予測がつきます。
(12) \(x^{2}+24\times 7x+2^{7}\times 7^{2}\)
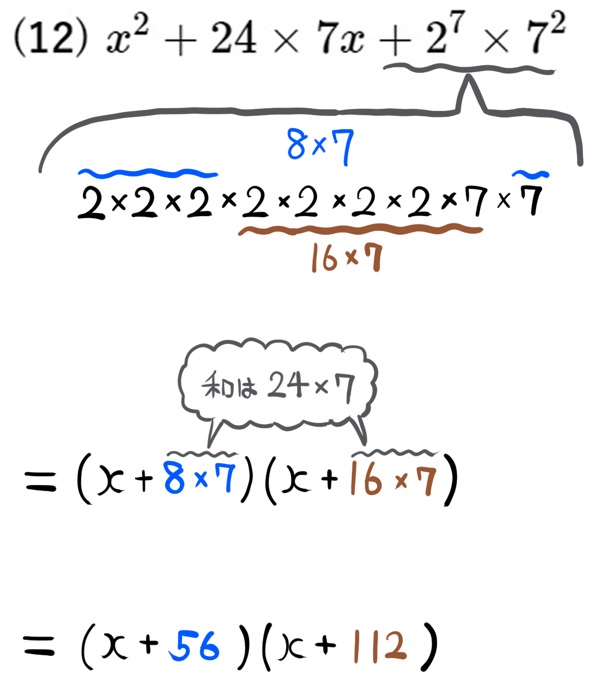
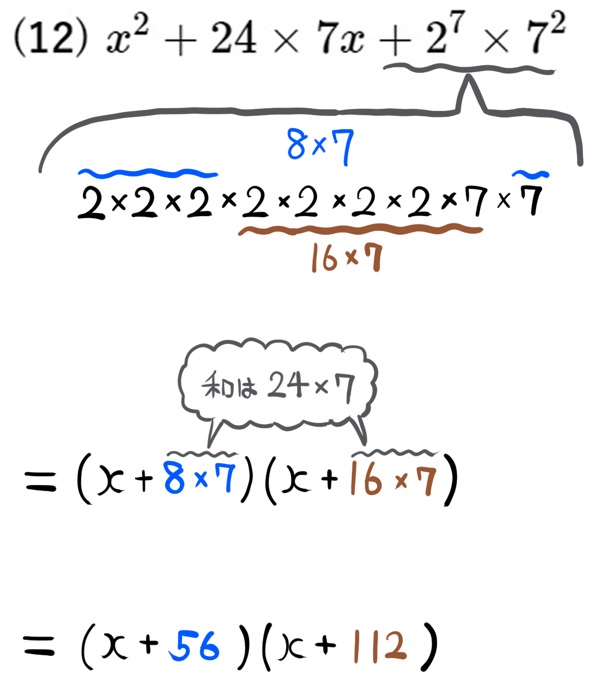

にゃんこ
係数や定数の大きい因数分解の解き方の練習は以上になります。

坂田先生
ここで学習したパターンをはじめ、因数分解の難問パターンをまとめて練習したい方はこちら↓で解きまくってください。

にゃんこ
難易度別にたくさんの問題があります。





























\(x^{2}y-xy-156y\)