


- 偶数と奇数の和が奇数になることの証明|間違い例
- 模範解答例
- 類題
- ミスしやすいポイントと証明が苦手な人用の勉強方法

偶数足す奇数が奇数になることの証明|間違い例

その和はn+2n=3nなので
これは3×奇数なので、n+2nは奇数となる
よって偶数足す奇数が奇数になることが証明された

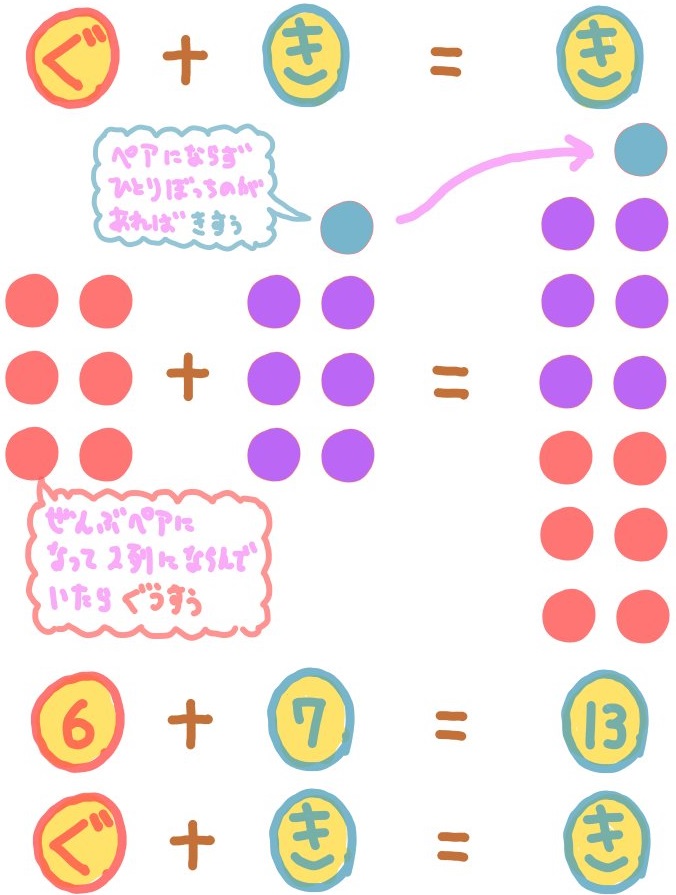
偶数と奇数の和が奇数になることを証明せよ、などという問題の場合『たがいに無関係な偶数と奇数を足して奇数になることを証明せよ』という意味になります。

ところがこの証明方法だと、nを奇数として、その2倍の2nを偶数とおいて証明を進めてしまっています。
例えば
nが1のとき2nは2
nが3のとき2nは6
nが5のとき2nは10
nが7のとき2nは14
・
・
・
といったように、限定された奇数と偶数の組み合わせのみで証明してしまっている、という点が間違いポイントです。
問題文は、どんな偶数と奇数をランダムに選んでもその和が奇数になることを証明せよという意味ですので、偶数と奇数は互いに無関係でなければなりません。
nを整数とし、
2nを偶数、2n+1を奇数とする
偶数2nと奇数2n+1の和は
\(2n+2n+1=4n+1\)
nは整数なので4nは偶数となり、4n+1は奇数となる
よって、偶数足す奇数は奇数となることが証明された

つまり、たがいに無関係な偶数と奇数の和が奇数になることを証明しなければいけないのに、それができていない、ということですね。

nを整数として2nを偶数とする、ところまではよかったのですが、2n+1を奇数としたところがまずかったですね。
これだと『連続する偶数と奇数の和が奇数になることを証明した』ようなものです。
たとえば
2nが2のとき、2n+1が3
2nが4のとき、2n+1が5
2nが6のとき、2n+1が7
2nが8のとき、2n+1が9
・
・
・
というように、連続した偶数と奇数の組み合わせに限定して、その和が奇数になるということを証明してしまったのです。
以上の理由により、この証明方法は間違った解答ということになります。
模範解答例

偶数を2nと、奇数を2m+1をする
その和は
\(2n+2m+1=2\left( n+m\right) +1\)
n+mは整数なので、2(n+m)は偶数となり、2(n+m)+1は奇数となる
したがって偶数と奇数の和は奇数となる


n+mは整数であることをなぜ書く必要があるのか?
ある数が偶数であることを示したい場合、それが『2×整数というかたち』になっていてはじめて2×整数は偶数だということが言えます。


たとえば2×3.5といったように小数をかけた場合
2×3.5=7となり、偶数にはならない場合が出てきますよね。
なのでわざわざn+mは整数である、と確認しておいて
2×(n+m)は2×(整数)のかたちなんですよ、とアピールしているワケです。

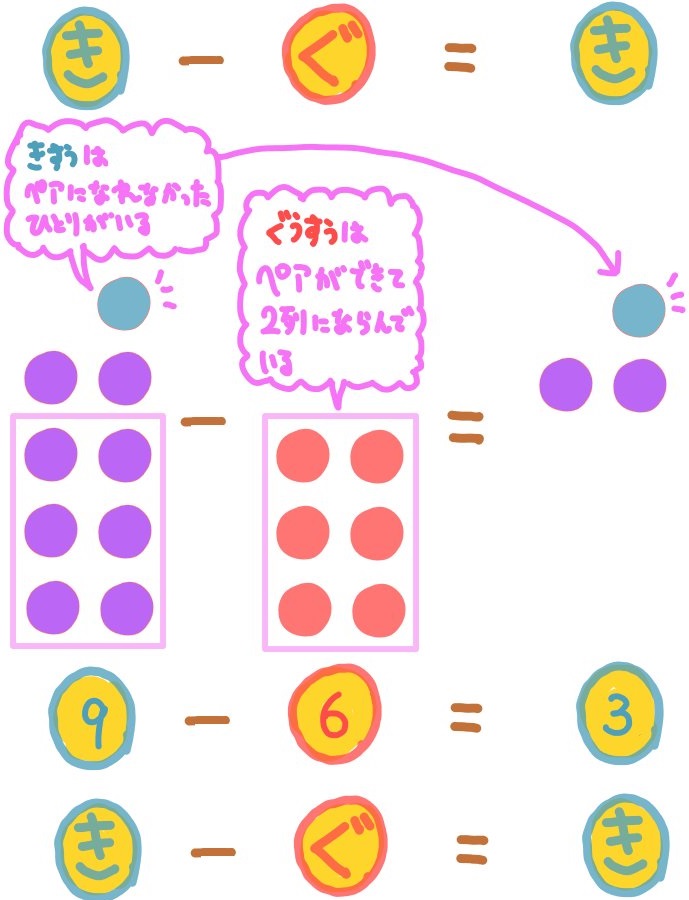
類題の解説

偶数を2nと、奇数を2m+1をする
その差は
\(2n-2m+1=2\left( n-m\right) +1\)
n-mは整数なので、2(n-m)は偶数となり、2(n-m)+1は奇数となる
したがって偶数と奇数の差は奇数となる


偶数を2nと、奇数を2m+1をする
その積は
\(2n\left( 2m+1\right) =4nm+2n=2\left( 2nm+n\right) \)
n、mは整数なので、2nm+nは整数となり、となり、 \(2\left( 2nm+n\right)\) は偶数となる
したがって偶数と奇数の積は偶数となる
2nを偶数、2n+1を奇数とする
偶数2nと奇数2n+1の和は
\(2n+2n+1=4n+1\)
nは整数なので4nは偶数となり、4n+1は奇数となる
よって連続する2数の整数の和が奇数になる
連続する2数の整数をn、n+1とする
その和はn+n+1=2n+1
nは整数なので、2n+1は奇数となる
よって連続する2数の整数の和は奇数となる


証明で気を付けるべきポイントと証明が苦手な人用の勉強方法
気を付けるべきポイント
最初の問題を例にあげるなら、「n+mは整数であることをなぜ書く必要があるのか?」で解説したように、偶数であることを証明しようとする場合『2×整数のかたち』になっていないと証明できたことになりません。

僕の経験上、このポイントで間違ってしまう方が、かなりいらっしゃいます。
なので、文字式で証明する際には、このポイントに気をつけてください。
証明問題が苦手な場合の練習方法
まず、問題を理解する。
次に、解答を読み、どのような手順で証明しているのかを理解する。
解答を見ながら、その証明の、大きな流れがどうなっているかを自分の言葉で説明する。
次に証明を一行ずつ、自分の言葉で説明していく。
(この一行はココとココが同じことを言っている、など)
ここで意味がわからない部分が出てくることもよくあります。
そんな場合は、調べるか、誰か知っている先生などに聞いて、解消しておくといいでしょう。
スラスラ言える状態になって初めて、書く練習をします。






























